Hearn E.J. Mechanics of Materials. Volume 1
Подождите немного. Документ загружается.


Shear
Stress
Distribution 173
moments about
D
is small (the shear centre is the required point through which
load
must
be
applied to produce
zero
twist of the section).
Thus taking moments offorces about
D
for equilibrium,
Q
xe
x
lo-’
=
2F,
x
25
x
10-3+2F,
x
25
x
lo-’
=
50
x
x
3.09
Q
x
lo3
x
(10
x
1.3
x
=
13.866Q
x
e
=
13.87mm
Thus, loads must
be
applied through the point
E,
13.87 mm to the left of the web centre-line
for zero twist of the section.
Problems
7.1
(A/B). A uniform I-section beam has
flanges
150
mm wide by
8
mm
thick and a web 180
mm
wide and 8
mm
thick. At
a
certain
section
there is
a
shearing force of 120 kN. Draw a diagram to illustrate the distribution of shear
stress
across
the section as
a
result of bending.
What
is the maximum shear stress? C86.7 MN/m2.]
7.2
(A/B). A girder has a uniform
T
cross-section with flange 250 mm
x
50 mm and web 220mm
x
50mm. At
a
certain section of the girder there is
a
shear force of 360 kN.
Plot neatly to scale the shear-stress distribution across the section, stating the values:
(a) where the web and the flange of the section meet;
(b)
at the neutral axis.
[B.P.]
C7.47, 37.4, 39.6MN/m2.]
7.3
(A/B). A
beam
having an inverted
T
cross-section has an overall width of 150mm and overall depth of
Momm. The thickness of the crosspiece is
50
mm and of the vertical web 25 mm. At
a
certain section
along
the beam
the
vertical
shear force is found to
be
120 kN. Draw neatly to scale, using 20 mm spacing except where closer intervals
arc
required,
a
shear-stress distribution diagram
across
this section. If the mean stress is calculated over the whole of
the
cross-sectional
area,
determine the ratio of the maximum shear stress to the mean shear stress.
[B.P.] C3.37.1
7.4
(AB).
The
channel section shown in Fig.
7.17
is simply supported over
a
span of
5
m and
carries
a
uniformly
distributed
load
of
15
kN/m
run
over
its whole length. Sketch the shearing-stress distribution diagram at the point of
maximum
shearing
forcc
and
mark important values. Determine the ratio of the
maximum
shearing
stress
to the
average
rhearing
stress.
[B.P.] [3,9.2, 9.3MN/mZ; 242.1
30
mm
30
mm
-4
t-125mm-9
I-
I--li-
30
Fig.
mm
7.17.

174
Mechanics
of
Materials
7.5
(A/B). Fig.
7.18
shows the cross-section of
a
beam which carries a shear
force
of
20
kN. Plot
a
graph to scale
CI.Mech.E.1 C21.7, 5.2, 5.23 MN/m*.]
which shows the distribution
of
shear stress due to bending across the cross-section.
7.6
(B). Show that the difference between the maximum and mean shear stress in the web of an I-section
beam
is
-where
Q
is the shear force on the cross-section,
h
is the depth of the web and
I
is the second moment of area of the
241
cross-section about the neutral axis
of
bending. Assume the I-section to be built
of
rectangular sections, the flanges
having width
B
and thickness
t
and the web a thickness
b.
Fillet radii are to be ignored.
[
I.Mech.E.1
7.7
(B).
Deduce an expression for the shearing stress at any point in
a
section of
a
beam
owing to the shearing
force at that section. State the assumptions made.
A
simply supported beam carries
a
central load
W.
The cross-section
of
the
beam
is rectangular of depth d. At what
distance from the neutral axis will the shearing stress be equal to the mean shearing stress on the section?
[U.L.C.I.] [d/fi.]
7.8
(B).
A
steel
bar
rolled to the section shown in Fig. 7.19 is subjected to
a
shearing force of 200 kN applied in the
direction
YY
Making the
usual
assumptions, determine the average shearing stress at the sections
A,
E,
C
and
D,
and
find the ratio
of
the maximum to the mean shearing stress in the section. Draw to scale a diagram to show the
variation
of
the average shearing stress
across
the section.
[U.L.]
[Clue:
treat
as
equivalent section similar to that of Example 7.3.1 C7.2, 12.3, 33.6, 43.8 MN/m2, 3.93.1
QhZ
I
Y
Fig. 7.19.
7.9
(C).
Usingcustomary notation, show that the shear stress over the cross-section of a loaded
beam
is given by
QAY
Ib
7=-.
The cross-section
of
a beam is an isosceles triangle of base Band height
H,
the
base
being arranged in
a
horizontal
plane. Find the shear stress at the neutral
axis
owing to a shear force
Q
acting
on
the cross-section and express it in
terms of the mean shear stress.
1
8Q .4
[U.L.C.I.]
-
-Tmcan.
[3B€f’ 3
(The second moment of area of a triangle about its
base
is
BH3/12.)

Shear
Stress
Distribution
175
7.10
(C).
A hollow steel cylinder, of 200 mm external and
100
mm internal diameter, acting as a
beam,
is subjected
to a shearing force
Q
=
10
kN perpendicular to the axis. Determine the mean shearing stress across the section and,
making
the usual assumptions, the average shearing stress at the neutral axis and at sections
25,50
and
75
mm from
the neutral
axis
as
fractions of the mean value.
Draw a diagram to show the variation of average shearing stress across the section of the cylinder.
[U.L.]
C0.425
MN/m2;
1.87, 1.65, 0.8, 0.47
MN/m2.]
7.11
(C).
A hexagonalcross-section bar is used
as
a beam with its greatest dimension vertical and simply
supported at its ends. The
beam
carries a central load of
60
kN. Draw a stress distribution diagram for a section of the
beam
at quarter
span.
All sides of the bar have a length of
25
mm.
(IN.*.
for triangle
=
bh3/36
where
b
=
base and
h
=
height.)
[O,
9.2,
14.8,
25.9
MN/mZ at
12.5
mm intervals above and below the N.A.]

CHAPTER
8
TORSION
Sommary
For
a
solid
or
hollow
shft
of uniform circular cross-section throughout its length, the
theory of pure torsion states that
T
T
GO
J
R=L
-=-
where Tis the applied external torque, constant over length
L;
J
is the polar second moment of area of shaft cross-section
x(D4
-
d
4,
for a hollow shaft;
xD4
32
32
=
-
for a solid shaft and
D
is the outside diameter;
R
is the outside radius;
d
is
the inside diameter;
T
is the shear stress at radius
R
and
is
the maximum value for both solid and hollow
shafts;
G
is the modulus of rigidity (shear modulus); and
8
is the angle of twist in
radians
on a length
L.
For
very thin-walled hollow shafts
J
=
2nr3t,
where
T
is
the mean radius of the shaft wall and
t
is the thickness.
Shear stress and shear strain are related to the angle of twist thus:
GB
L
T=-R=G~
Strain energy in torsion
is given by
U=-
x
volume for
solid shafis
2GJ
2L
For
a
circular shaft subjected to
combined bending
and
torsion
the
equivalent bending
moment
is
Me
=
i[M
+
J(Mz
+T
')I
and the
equivalent torque
is
where
M
and T are the applied bending moment and torque respectively.
The
pa~er
transmitted
by a shaft carrying torque Tat
o
rad/s
=
To.
T,
=
+J(
M
+T
2,
176

§8.1
177
Torsion
8.1. Simple torsion theory
When a uniform circular shaft is subjected to a torque it can be ShOWn that every sectiOn of
the shaft is subjected to a state of pure shear (Fig. 8.1 ), the moment of resistance developed by
the shear stresses being everywhere equal to the magnitude, and opposite in sense, to the
applied torque. For the purposes of deriving a simple theory to describe the behaviour of
shafts subjected to torque it is necessary to make the following basic assumptionS:
(1) The material is homogeneous, i.e. of uniform elastic properties throughout.
(2) The material is elastic, following Hooke's law with shear stress proportional to shear
strain.
(3) The stress does nOt exceed the elastic limit or limit of proportionality.
(4) Circular SectiOnS remain circular.
(5) Cross-sectioDS remain plane. (This is certainly nOt the case with the torsion of DOD-
circular SectiOnS.)
(6) Cross-sectioDS rotate as if rigid, i.e. every diameter rotates through the same angle.
Fig. 8.1. Shear system set up on an elem-ent in thesufface of a shaft subjected to torsion.
Practical tests carried out on circular shafts have shown that the theory developed below on
the basis of these assumptions shows excellent correlation with experimental results.
(a) Angle of twist
Consider now the solid circular shaft of radius R subjected to a torque T at one end, the
other end being fixed (Fig. 8.2). Under the action of this torque a radial line at the free end of
the shaft twists through an angle 9, point A moves to B, and AB subtends an angle y at the
fixed end. This is then the angle of distortion of the shaft, i.e. the shear strain.
SinCe angle in radians = arc + radius
arc AB = R8 = Ly
y = R8/ L (8.1)
From the definition of rigidity modulus
shear stress T
shear strain y
G=
178
Mechanics
of
Materials
$8.1
T
..
Fig.
8.2.
T
y=-
G
where
T
is the shear stress set up at radius
R.
Therefore equating eqns.
(8.1)
and (8.2),
where
T'
is the shear stress at any other radius
r.
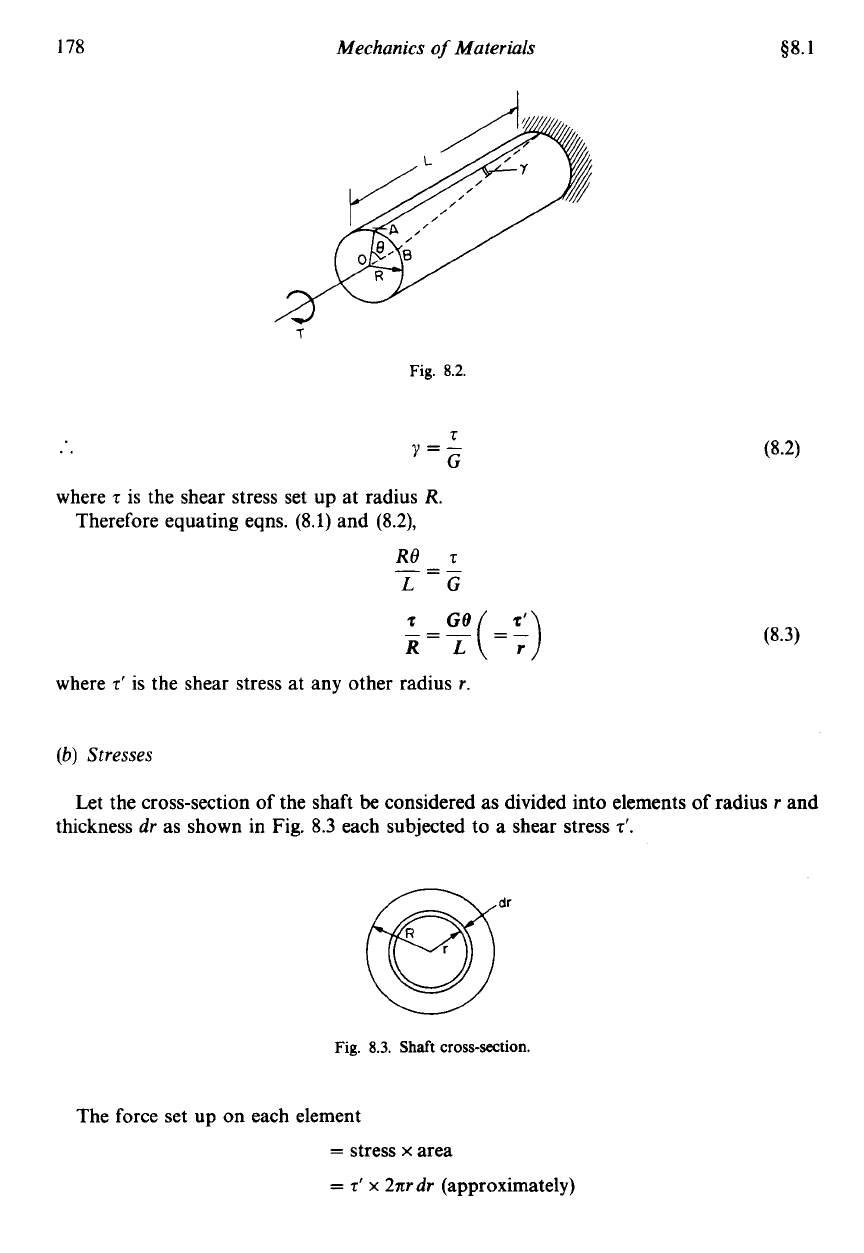
(b)
Stresses
Let the cross-section of the shaft
be
considered as divided into elements
of
radius
r
and
thickness
dr
as shown in Fig.
8.3
each subjected to a shear stress
z'.
Fig.
8.3.
Shaft
cross-section.
The force set up on each element
=
stress
x
area
=
2'
x
2nr
dr
(approximately)

$8.2 Torsion
179
This force will produce a moment about the centre axis of the shaft, providing a contribution
to the torque
=
(7'
x
2nrdr)
x
r
=
2n7'r2
dr
The total torque on the section
T
will then be the sum of all such contributions across the
section,
i.e.
T
=
2nz'r2dr
i
J
0
Now the shear stress
z'
will vary with the radius rand must therefore be replaced in terms
of
r
before the integral is evaluated.
From eqn.
(8.3)
R
..
0
=
E
L
jkr3 dr
0
The integral
5
0"
2nr3 dr
is
called the
polar second
moment
of
area
J,
and may be evaluated
as
a
standard form for solid and hollow shafts as shown in
$8.2
below.
GO
L
T=-J
..
or
T
GO
JL
=-
-
Combining eqns.
(8.3)
and
(8.4)
produces the so-called simple theory of torsion:
T
z
G8
--
-
J-R-L
8.2. Polar
second
moment
of
area
As
stated above the polar second moment
of
area
J
is
defined as
J
=
2nr3dr
0
i'

180
For
a
solid
shafi,
Mechanics
of
Materials
nD*
or
-
4
32
2n~4
=-
For
a
hollow
shaft
of internal radius
r,
J=2n r3dr=2n
-
i
[:I:
x x
=
-(R4-r4)
or
-(D4-d*)
2 32
$8.3
For
thin-walled
hollow
shafis
the values of
D
and
d
may
be
nearly
equal,
and
in such
cases
there
can
be
considerable errors in using the above equation involving the difference of two
large quantities of similar value. It
is
therefore convenient to obtain an alternative form of
expression for the polar moment of area.
Now
J
=
2nr3dr
=
C(2nrdr)r’
=
AY’
0
i
where
A
(
=
2nr
dr) is the area of each small element of Fig.
8.3,
i.e.
J
is the sum of the
Ar2
terms for all elements.
If a thin hollow cylinder is therefore considered as just one
of
these small elements with its
wall thickness
t
=
dr,
then
J
=
Ar’
=
(2nrt)r’
=
2xr3t
(approximately)
(8.8)
8.3.
Shear
stress
and shear strain
in
shafts
The shear
stresses
which are developed in a shaft subjected to pure torsion are indicated in
Fig.
8.1,
their values being given by the simple torsion theory as
GO
L
7=-R
Now from the definition of the
shear
or rigidity modulus
G,
r
=
Gy
It therefore follows that the two equations
may
be
combined to relate the shear stress
and
strain in the shaft to the angle of twist per unit length, thus

$8.4
Torsion
181
or, in terms of some internal radius
r,
(8.10)
These equations indicate that the shear stress and shear strain
vary
linearly with radius and
have their maximum value at the outside radius (Fig.
8.4).
The applied shear stresses
in
the
plane of the cross-section are accompanied by complementary stresses of equal value
on
longitudinal planes as indicated in Figs.
8.1
and
8.4.
The significance of these longitudinal
shears to material failure is discussed further in
88.10.
Fig.
8.4.
Complementary longitudinal
shear
stress
in
a
shaft
subjected
to
torsion.
8.4.
Section
modulus
It is sometimes convenient to re-write part of the torsion theory formula to
obtain
the
maximum shear stress in shafts
as
follows:
TT
JR
-=-
With
R
the outside radius of the shaft the above equation yields the greatest value possible
for
T
(Fig.
8.4),
i.e.
TR
7-=
-
J
T
Z
T-=-
..
(8.11)
where
2
=
J/R
is termed the
polar
section
modulus.
It will
be
seen
from the preceding section
that:
nD3
16
Z=-
(8.12)
for solid
shafts,
and for hollow shafts,
~(D1-d~)
160
Z-
(8.13)

182
Mechanics
of
Materials
$8.5
8.5.
Torsional rigidity
The angle of twist per unit length of shafts is given by the torsion theory as
e~
L=GJ
-
The quantity
GJ
is termed the
torsional rigidity
of the shaft and is thus given by
T
GJ
=-
91~
(8.14)
i.e. the torsional rigidity is the torque divided by the angle of twist (in radians) per unit length.
8.6.
Torsion of hollow shafts
It has been shown above that the maximum shear stress in a solid shaft is developed in the
outer surface, values at other radii decreasing linearly to zero at the centre. It is clear,
therefore, that if there is to be some limit set on the maximum allowable working stress in the
shaft material then only the outer surface of the shaft will reach this limit. The material within
the shaft will work at a lower stress and, particularly near the centre, will not contribute as
much to the torque-carrying capacity of the shaft. In applications where weight reduction is
of prime importance as in the aerospace industry, for instance, it is often found advisable to
use hollow shafts.
The relevant formulae for hollow shafts have been introduced in
$8.2
and will not be
repeated here.
As
an example of the increased torque-to-weight ratio possible with hollow
shafts, however, it should be noted for a hollow shaft with an inside diameter half the outside
diameter that the maximum stress increases by
6
%
over that for a solid shaft of the same
outside diameter whilst the weight reduction achieved is approximately
25
%.
8.7.
Torsion of thin-walled tubes
The torsion
of
thin-walled tubes
of
circular and non-circular cross-section is treated fully
in
Mechanics
of
Materials
2.
t
8.8.
Composite shafts
-
series connection
If two or more shafts of different material, diameter or basic form are connected together in
such a way that each carries the same torque, then the shafts are said to be connected in series
and the composite shaft
so
produced is therefore termed
series-connected
(Fig.
8.5)
(see
Example
8.3).
In such cases the composite shaft strength is treated by considering each
component shaft separately, applying the torsion theory to each in turn; the composite shaft
will therefore
be
as weak as its weakest component. If relative dimensions of the various parts
are required then a solution is usually effected by equating the torques in each shaft, e.g. for
two shafts in series
T=-----
GlJlO1
=-
Ll
L2
t
E.
J.
Hearn,
Mechanics
of
Materials
2,
3rd edition (Butterworth-Heinemann, Oxford,
1997).
(8.15)
