Hearn E.J. Mechanics of Materials. Volume 1
Подождите немного. Документ загружается.

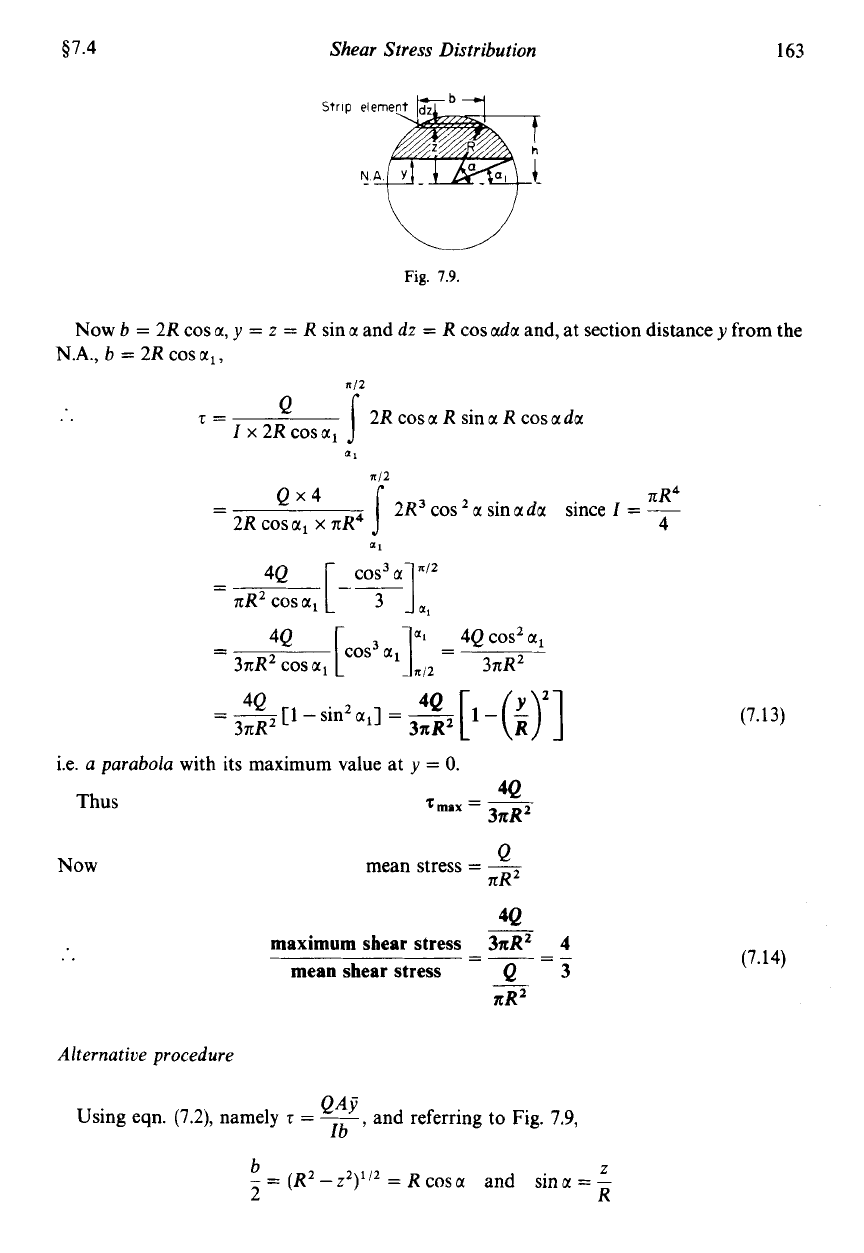
$7.4
Shear
Stress Distribution
163
m
Fig.
1.9.
I
.aw
b
=
2R
cos a,
y
=
z
=
R
sin a and dz
=
R
cos ada anL, at section distance
y
from the
N.A.,
b
=
2R
cosal,
nlZ
2R
cosa
R
sin a
R
cosada
I
x
2R
cos a,
..
z=
nR4
2R3
cos a sin a du since
I
=
__
2R
cosal
x
nR4
4
-
-
- -
4Q
[cos3al]
=
4Qcos2a1
-
4Q
3nR2
cos a1
n/Z
3ZRZ
[I
-
sinZ all
=
-
3nRZ
3nR2
--
i.e. a parabola with
its
maximum value at
y
=
0.
Thus
Now
4Q
z
msx
=
-
3nR2
Q
mean stress
=
nR
4Q
maximum shear stress 3aR2
4
..
=-=-
mean shear stress Q3
ZR2
Alternative procedure
Using eqn.
(7.2),
namely
7
=
w,
and referring
to
Fig.
7.9,
Ib
(7.13)
(7.14)
b
Z
-
=
(Rz
-z2)'/'
=
R
cosa and
sin
a
=
-
2
R

164
Mechanics
of
Materials
57.5
Aj
for the shaded segment
=
Aj
for strip element
R
sin
1
a
=
1
bdzz
=
2
1
(R2
-z2)'12zdz
R
sin
a
R
sin
a
2
312
Rsina
=$[(R2-z)
1,
=
%[R2(1
-sin2u)]3i2
=
5
R3
(cos2
u)312
=
3
R3
cos3 a
since
..
QAj
-
Q
x
3R3
cos3
a
7=--
Ib nR4
-
x
2R
cosu
4
IZ
R4
I=-
4
cos2
u
=
~
4Q
[I
-sin2al
4Q
7=-
3nR2 3zR2
(7.13) bis.
7.5.
Limitation
of
shear stress distribution theory
There are certain practical situations where eq. (7.2) leads to an incomplete solution and it
is
necessary to consider other conditions, such as equilibrium at a free surface, before a valid
solution is obtained. Take, for example, the case
of
the bending of a bar or beam having a
circular cross-section as shown in Fig. 7.10(a).
The shear stress distribution across the section owing
to
bending is given by eqn. (7.2) as:
(7.15)
At some horizontal section
AB,
therefore, the shear stresses will be as indicated in Fig. 7.10,
and will
be
equal along
AB,
with a value given by eqn. (7.15).
Now, for an element at
A,
for example, there should
be
no component of stress normal to
the surface since it is unloaded and equilibrium would not result. The vertical shear given by
the equation above, however, clearly would have a component normal to the surface.
A
valid
solution can only
be
obtained therefore if a secondary shear stress
7xz
is set up in the
z
direction which, together with
T~~,
produces a resultant shear stress tangential to the free
surfacesee Fig. 7.10(b).
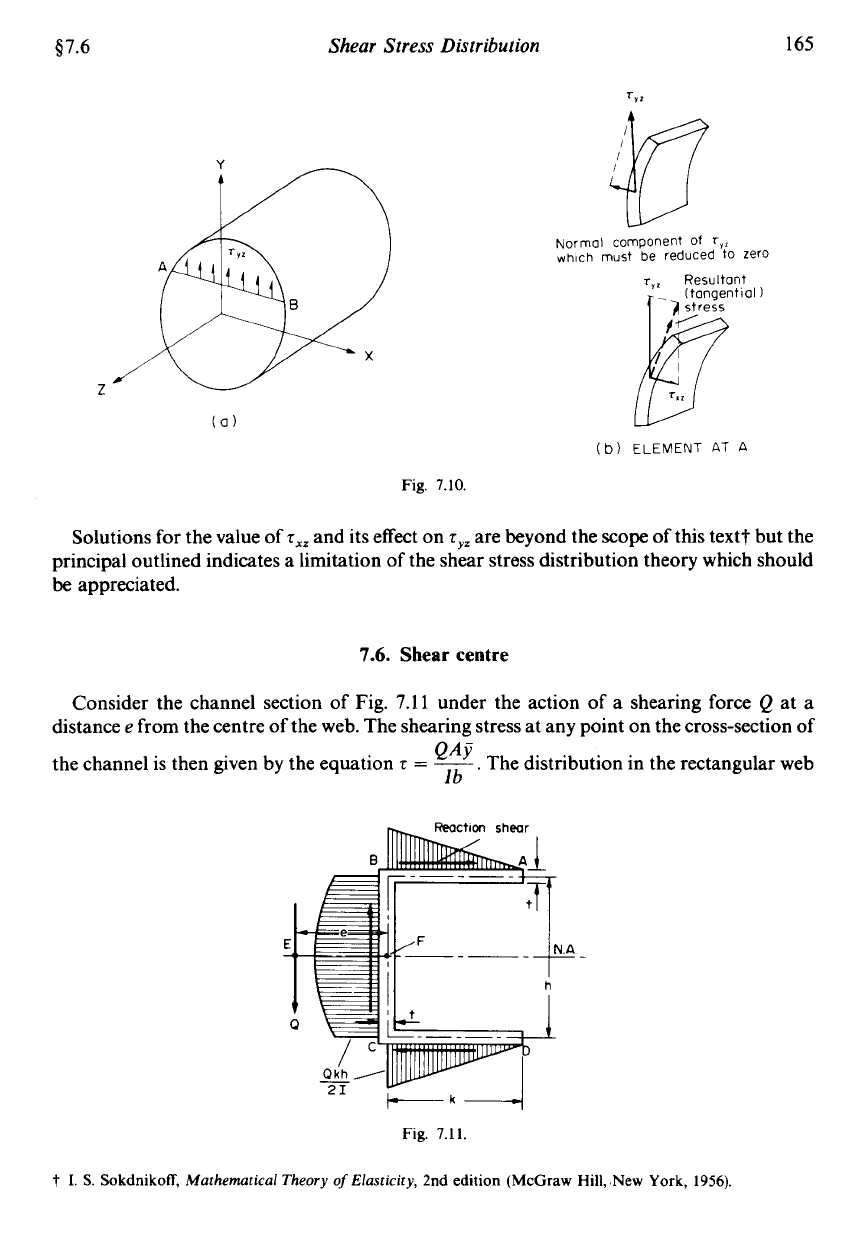
$7.6
Shear Stress Distribution
165
Fig.
7.10.
Normal component
of
rrz
which
must be reduced
to
zero
rYz
Resultant
jg
(tangential)
r.,
(b)
ELEMENT AT
A
Solutions for the value of
T,,
and its effect on
T~,
are beyond the
scope
of this text? but the
principal outlined indicates a limitation
of
the shear stress distribution theory which should
be
appreciated.
7.6.
Shear centre
Consider the channel section
of
Fig. 7.11 under the action of a shearing force
Q
at a
distance
e
from the centre
of
the web. The shearing stress at any point on the cross-section of
the channel is then given by the equation
z
=
E.
The distribution in the rectangular web
Ib
Fig.
7.11.
t
I.
S.
Sokdnikoff,
Mathematical Theory
of
Elasticity,
2nd edition (McGraw Hill,.New York,
1956).

166
Mechanics of Materials
$7.6
will be parabolic, as previously found, but will not reduce to zero at each end because of the
presence of the flange areas.
When the stress in the flange is being determined the breadth
b
is replaced by the thickness
t,
but
I
and
jj
still refer to the N.A.
QAy Qxkt h Qkh
zg
=
~
=-
x-=-
It
It 2 21
Thus from eqn.
7.11,
and
zA
=
0
since area beyond
A
=
0
Between
A
and
B
the distribution is linear, since
z
is directly proportional to the distance
along
AB (Q, t,
hand
I
all being constant). An exactly similar distribution will be obtained for
CD.
The stresses in the flanges give rise to forces represented by
Qkh QkZht
average stress
x
area
=
3
x
-
x
kt
=
-
21
41
These produce a torque about
F
which must equal the applied torque, stresses in the web
producing forces which have no moment about
F.
Equating torques about
F
for equilibrium:
Qxe=- Qk2ht
41
k2
hZ
t
41
..
e=-
(7.16)
Thus if a force acts on the axis of symmetry, distance
e
from the centre of the web, there will
be no tendency for the section to twist since moments will be balanced. The point
E
is then
termed the
shear centre
of the section.
The shear centre of a section is therefore a’ejined as that point through which
load
must be
applied for
zero
twist of the section.
With loads applied at the shear centre of beam sections,
stresses will be produced due to pure bending, and evaluation of the stresses produced will be
much easier than would be the case if torsion were also present.
It should be noted that if a section has two axes of symmetry the point where they cross is
automatically the shear centre.
Examples
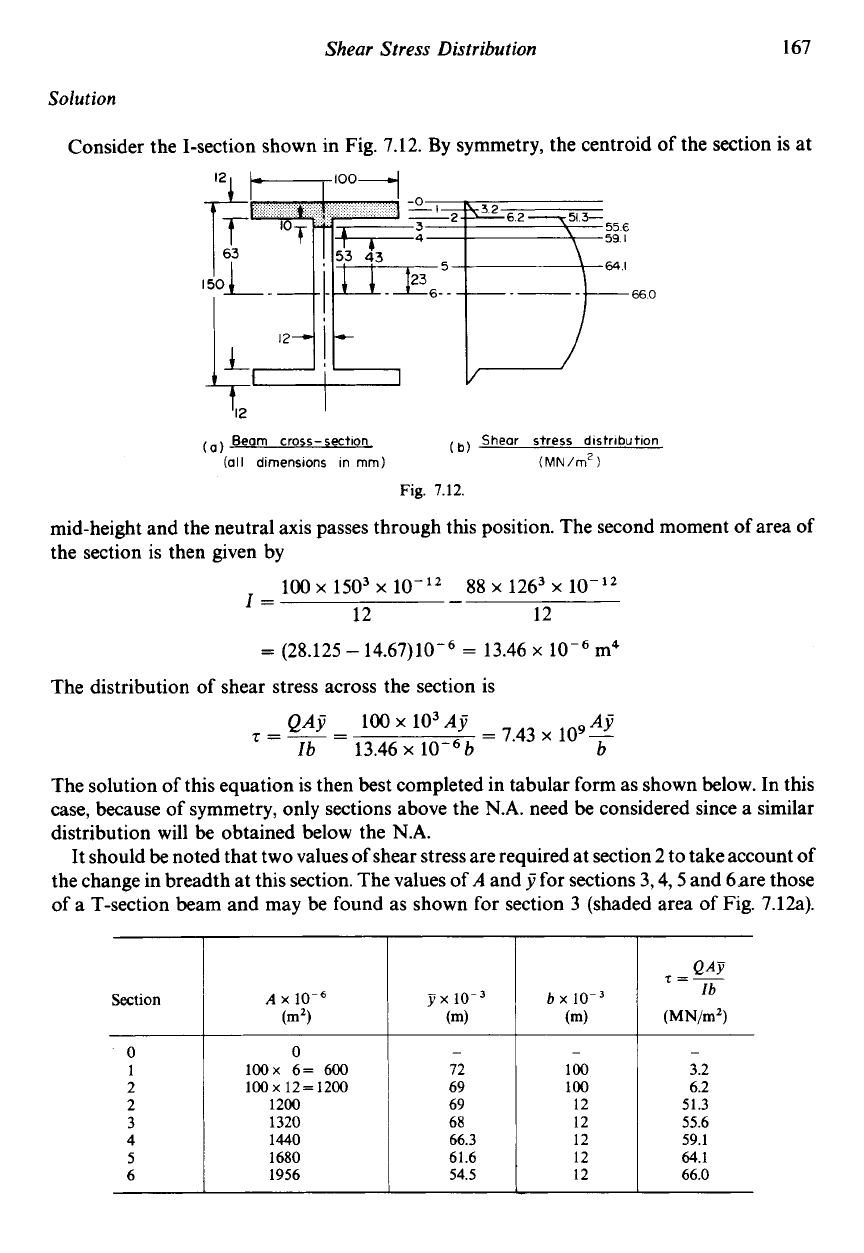
Example
7.1
At
a
given position on a beam of uniform I-section the beam is subjected to a shear force of
100 kN. Plot a curve to show the variation of shear stress across the section and hence
determine the ratio of the maximum shear stress to the mean shear stress.
Shear
Stress
Distribution
167
Solution
Consider the I-section shown in Fig. 7.12. By symmetry, the centroid of the section is at
112
I
(a)
Beam cross-section
b)
Shear stress distribution
Fig.
7.12.
mid-height and the neutral axis passes through this position. The second moment
of
area of
the section is then given by
(all
dimensions in
mm)
(MN/mz)
100
x
1503 x
88 x 1263 x
-
12 12
I=
=
(28.125
-
14.67)10-6
=
13.46
x
m4
The distribution of shear stress across the section is
QA~
ioox103~y
AY
r=--
-
=
7.43 x 109-
Ib
13.46 x
b b
The solution of this equation is then best completed in tabular form as shown below. In this
case, because of symmetry, only sections above the
N.A.
need
be
considered since a similar
distribution will
be
obtained below the
N.A.
It should
be
noted that two values of shear stress are required at section 2 to take account
of
the change in breadth at this section. The values of
A
and
jj
for sections 3,4,5 and 6are those
of a T-section beam and may be found as shown for section
3
(shaded area of Fig. 7.12a).
Section
A
x
(m2)
b
x
(m)
~
0
1
2
2
3
4
5
6
0
100~
6=
600
100x12=1200
1200
1320
1440
1680
1956
-
72
69
69
68
66.3
61.6
54.5
-
100
100
12
12
12
12
12
-
3.2
6.2
51.3
55.6
59.1
64.1
66.0

168 Mechanics
of
Materials
For section
3:
Taking moments about the top edge (Fig. 7.12a),
(100
x
12
x
6)1OP9
+
(10
x
12
x
17)10-9
=
(100
x
12+
10
x
12)h
x
where
h
is the centroid of the shaded T-section,
7200+2040= (1200+120)h
9240
1320
=
7mm
h=-
..
The distribution of shear stress due to bending
is
then shown in Fig. 7.12b, giving a maximum
shear stress oft,,,
=
66
MN/m*.
j3
=
75-7
=
68mm
Now the mean shear stress across the section is:
shear force 100
x
lo3
-
-
3.912
x
Zman
=
area
=
25.6 MN/m2
--=
-
66
2.58
max. shear stress
mean shear stress 25.6
Example
7.2
At a certain section a beam has the cross-section shown in Fig. 7.13. The beam is simply
supported at its ends and carries a central concentrated load of
500
kN together with a load of
300 kN/m uniformly distributed across the complete span of 3 m. Draw the shear stress
distribution diagram for a section 1 m from the left-hand support.
(a) Beam
cross-
section
(mm)
(b) Shear stress distribution
(
MN/m2)
Fig.
7.13.
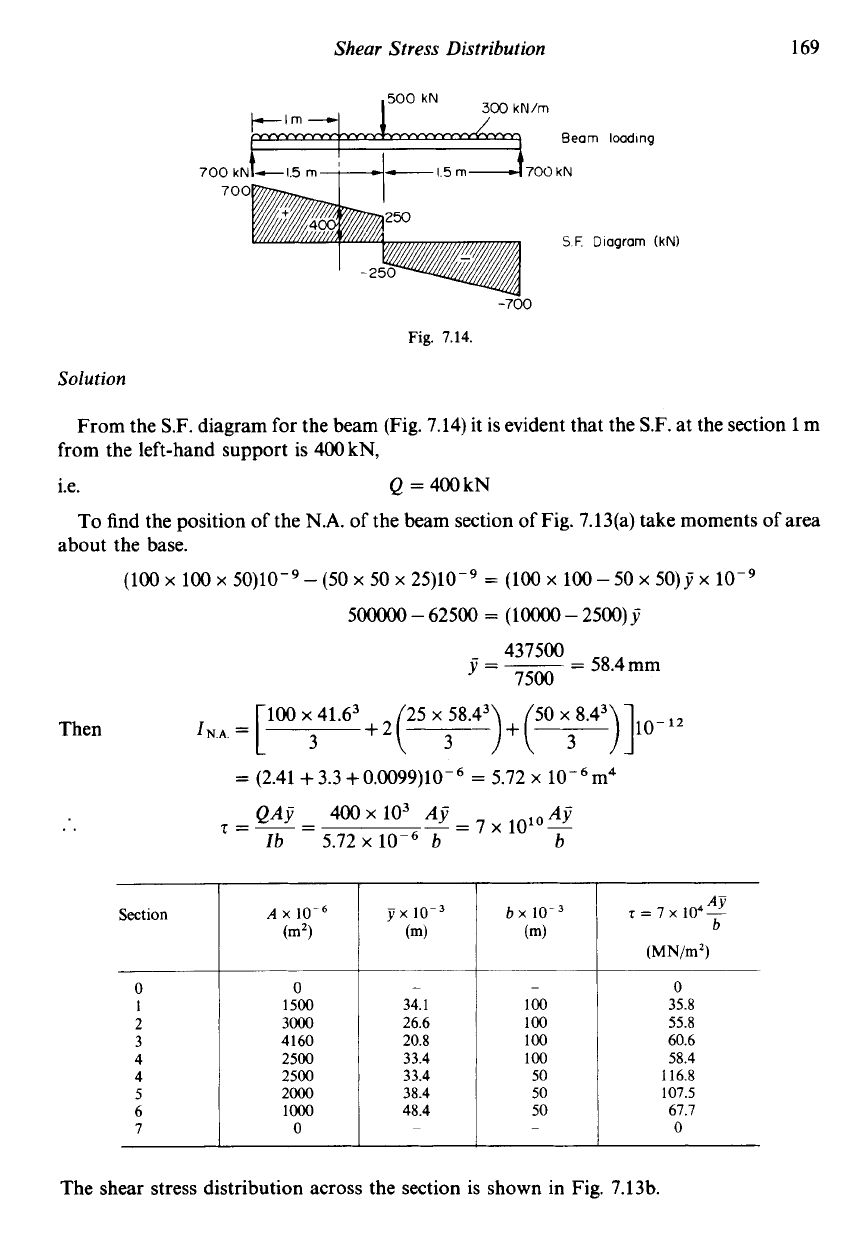
Shear Stress Distribution
169
300
kN/m
Beam
looding
700
kN
700
kN
Fig.
7.14.
Solution
From the S.F. diagram for the beam (Fig. 7.14) it is evident that the
S.F.
at the section 1 m
from the left-hand support is 400 kN,
i.e.
Q
=400kN
To find the position of the N.A. of the beam section of Fig. 7.13(a) take moments of area
about the base.
(100
x
100 x
50)10-’-
(50
x
50
x
25)10-’
=
(100
x
100-
50
x
50)j
x
lo-’
500000
-
62500
=
(loo00
-
2500)j
-
58.4mm
-
437500
y=--
7500
Then
I~.~.
=
[loo
x341.63
+
2
(
25
x
58.43
)
+
(
50
x
8.43
)]lO-lz
=
(2.41
+
3.3
+
0.0099)10-6
=
5.72
x
m4
Section
0
1
2
3
A
x
(m2)
5
=
7
x
104-
AL
b
0
1500
3000
4160
2500
2500
2000
1000
0
34.1
26.6
20.8
33.4
33.4
38.4
48.4
-
100
100
100
100
50
50
50
0
35.8
55.8
60.6
58.4
116.8
107.5
67.7
0
The shear stress distribution across the section is shown in Fig. 7.13b.
170
Mechanics
of
Materials
Example
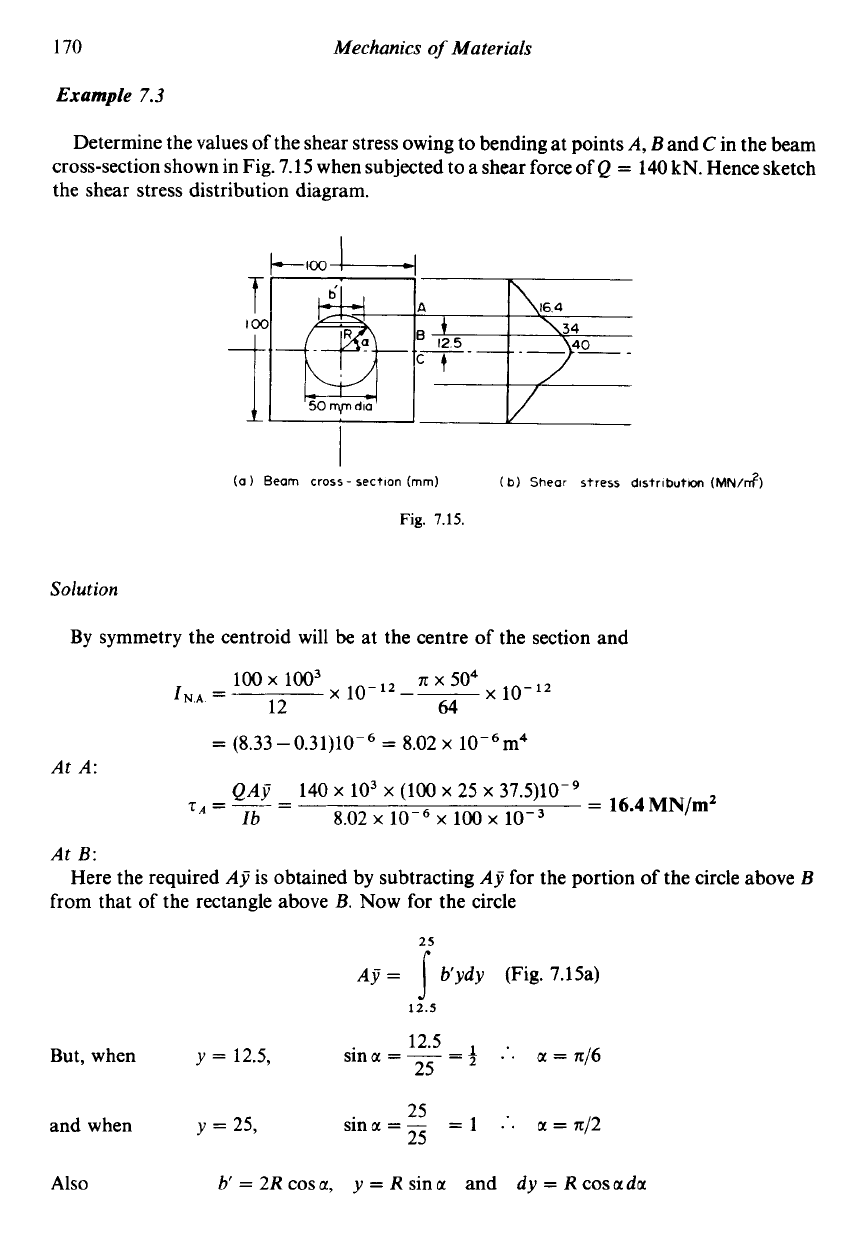
7.3
Determine the values of the shear stress owing to bending at points
A,
Band
C
in the beam
cross-section shown in Fig. 7.15 when subjected to a shear force
of
Q
=
140 kN. Hence sketch
the shear stress distribution diagram.
16.4
134
.-4L-
(b)
Shear
stress
distributm
(MN/&)
I
(a
1
Beam
cross-
section
(mm)
Fig.
7.15.
Solution
By symmetry the centroid will be at the centre of the section and
=
(8.33 -0.31)10-6
=
8.02
x
10-6m4
At
A:
QAy
140
x
lo3
x
(100
x
25
x
37.5)10-'
5*=-=
=
16.4MN/m2
Ib
8.02
x
10-6
x
100
x
10-3
At
B:
from that of the rectangle above
B.
Now for the circle
Here the required
Ay
is obtained by subtracting
Ay
for the portion
of
the circle above B
Ay
=
b'ydy (Fig. 7.15a)
J
12.5
12.5
25
sina
=-=$
.'.
a
=
n/6
But, when
y
=
12.5,
25
25
sina
=- =
1
.'.
a
=
42
and when y
=
25,
Also bf=2Rcosa, y=Rsina and dy=Rcosada
Shear Stress
Distribution
171
.’.
for circle portion,
Aj
=
2R cos
a
R sin
a
R cos
a
da
=
~2R’cos’osinada
n16
cos3a
n12
n16
=
2R3
[
-’.
for complete section above
B
and
..
..
At
C:
Ajj
=
100
x
37.5
x
31.25
x
=
110.25
x
10-6m3
-
6.75
x
b‘
=
2Rcosn/6
=
2
x
25
x
x
J3/2
=
43.3
x
m
b
=
(100-43.3)10-3
=
56.7
x
10-3m
QAjj
140
x
lo3
x
110.25
x
Ib
8.02
x
x
56.7
x
1O-j
TB=--
-
=
34MN/m2
A9
for semicircle
=
2R3
-___
[
cOs’al:
Ay
for section above
C
=
(100
x
50
x
25)10-9
-
10.41
x
=
114.59
x
10-6m3
and
..
5,
= =
40MN/m2
b=
(100-50)10-3
=
50~
10-3m
140
x
lo3
x
114.59
x
8.02
x
x
50
x
The total shear stress distribution across the section is then sketched in Fig. 7.1%.
Example
7.4
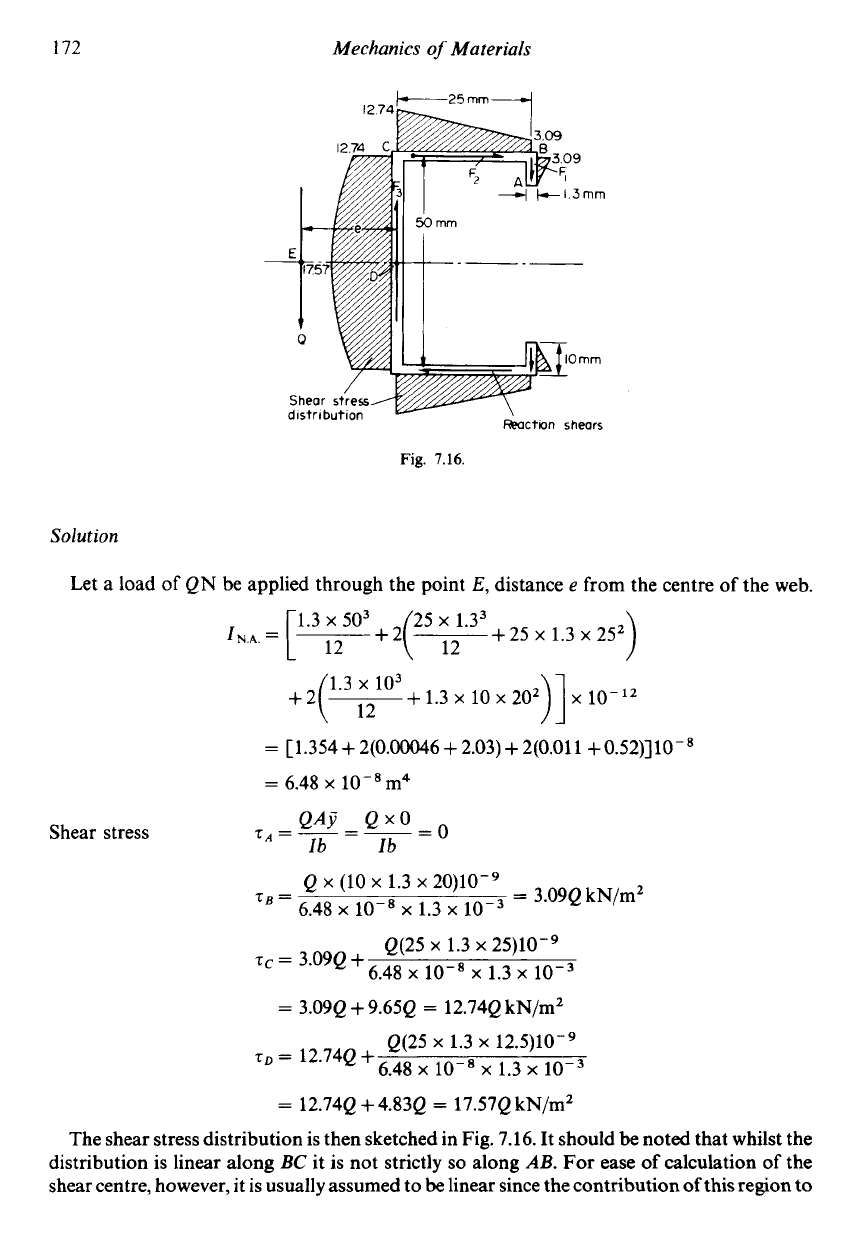
A
beam having the cross-section shown in Fig. 7.16 is constructed from material having a
constant thickness of 1.3 mm. Through what point must vertical loads
be
applied in order
that there shall be no twisting of the section? Sketch the shear stress distribution.
172
Mechanics
of
Materials
Fig.
7.16.
Solution
Let a load of
QN
be applied through the point
E,
distance
e
from the centre
of
the web.
1.3 x
503
25 x 1.33
IN.A.
=
[
12
+
2(
12
+
25
x
1.3 x 252)
=
[1.354+ 2(0.00046+2.03)+2(0.011 +0.52)]10-'
=
6.48 x
10-8m4
Shear stress
Q
x
(io
x
1.3
x
20)10-9
58
=
=
3.09Q
kN/m2
6.48 x
lo-'
x
1.3
x
Q(25
x
1.3
x
25)10-9
ZC
=
3.09Q
+
6.48 x
lo-'
x
1.3 x
=
3.09Q
+
9.65Q
=
12.74Q
kN/m2
Q(25 x 1.3 x 12.5)10-9
TD
=
12.74Q
+
6.48 x
lo-'
x 1.3 x
=
12.74Q
+
4.83Q
=
17.57Q
kN/m2
The shear stress distribution is then sketched in Fig.
7.16.
It should
be
noted that whilst the
distribution is linear along
BC
it
is
not strictly
so
along
AB.
For ease
of
calculation
of
the
shear centre, however, it is usually assumed to
be
linear since the contribution
of
this region to
