Hearn E.J. Mechanics of Materials. Volume 1
Подождите немного. Документ загружается.

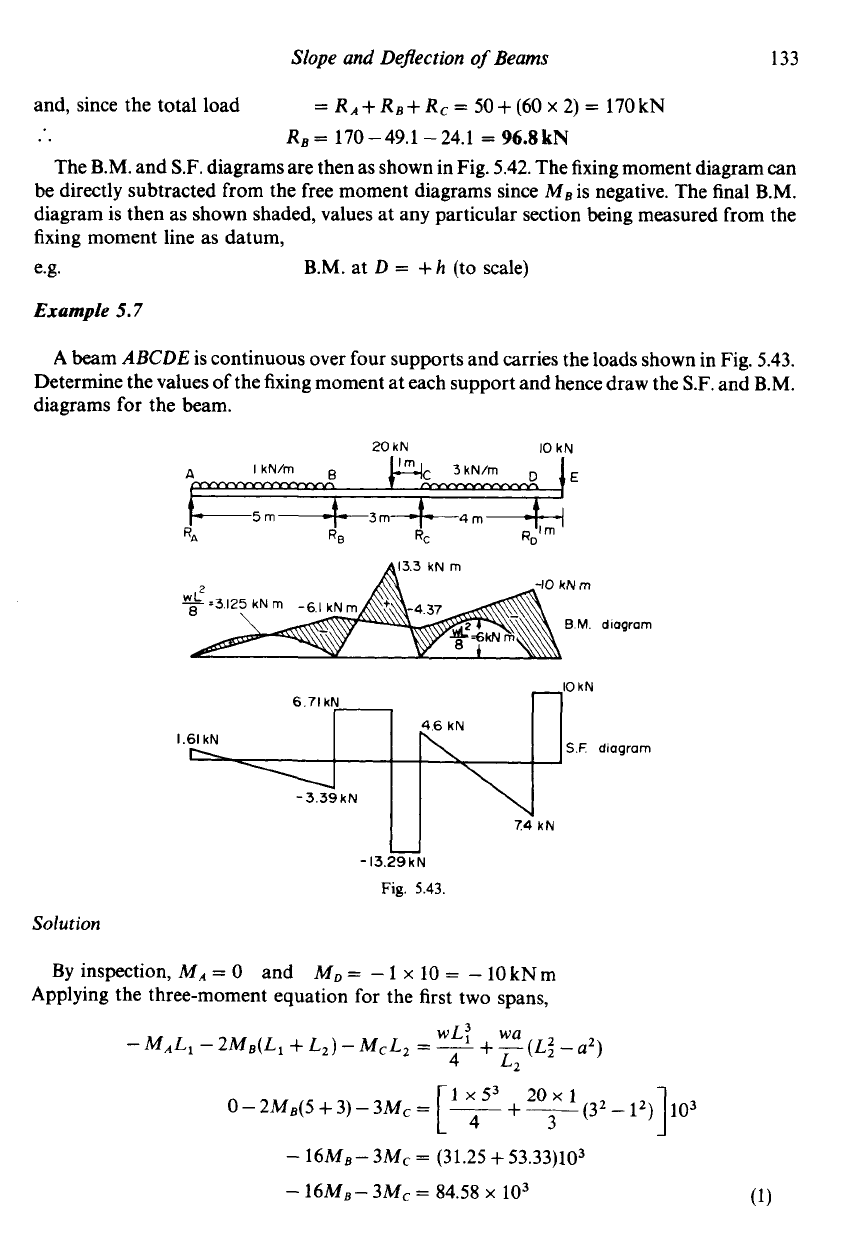
Slope and Defection
of
Beams
-3.39kN
133
24
kN
-
and, since the total load
..
=RA+RB+Rc=~O+(~OX~)=
170kN
RB
=
170-49.1 -24.1
=
96.8kN
The B.M. and S.F. diagrams are then as shown in Fig. 5.42. The fixing moment diagram can
be
directly subtracted from the free moment diagrams since MB is negative. The final B.M.
diagram is then as shown shaded, values at any particular section being measured from the
fixing moment line as datum,
e.g.
B.M.
at
D
=
+h
(to scale)
Example
5.7
A
beam
ABCDE
is continuous over four supports and carries the loads shown in Fig. 5.43.
Determine the values of the fixing moment at each support and hence draw the S.F. and B.M.
diagrams for the beam.
20
kN
10
kN
I
kN/m
A
A13.3
kN m
diagram
Solution
By inspection, MA
=
0
and MD
=
-
1
x
10
=
-
10
kNm
Applying the three-moment equation for the first two spans,
-
16MB- 3Mc
=
(31.25
+
53.33)103
-
16MB- 3Mc
=
84.58
x
lo3

134
Mechanics
of
Materials
and, for the second and third spans,
4
-3M~-2Mc(3+4)-(-10~10
-
~MB- 14Mc
+
(40
x
lo3)
=
(66.67
+
48)103
-
3MB- 14Mc
=
74.67
x
lo3
(2)
x
16/3
(3)
-
(1)
-
16MB- 74.67Mc
=
398.24
x
lo3
-
71.67Mc
=
313.66
x
lo3
Mc
=
-
4.37
x
lo3
Nm
Substituting in (l),
-
16~,
-
3(
-
4.37
x
103)
=
84.58
x
103
(84.58
-
13.11)103
16
Mg=
-
=
-
4.47 kN
m
Moments about
B
(to left),
5R,
=
(-4.47
+
12.5)103
RA
=
1.61 kN
Moments about
C
(to left),
RAx8-(1
x103x5x5.5)+(R,x3)-(20x103x
1)= -4.37~
lo3
3R,
=
-
4.37
x
lo3
+
27.5
x
lo3
+
20
x
lo3
-
8
x
1.61
x
lo3
3R,
=
30.3
x
lo3
RE
=
10.1 kN
Moments about
C
(to right),
(-
IOX
lo3
x
5)+4RD-(3
x
lo3
x
4
x
2)
=
-4.37
x
lo3
4R,
=
(
-
4.37
+
50
+
24)103
R,
=
17.4 kN
Then, since
RA
+
R,
+
R,+ R,
=
47kN
1.61
+
10.1
+
R,+ 17.4
=
47
R,
=
17.9
kN
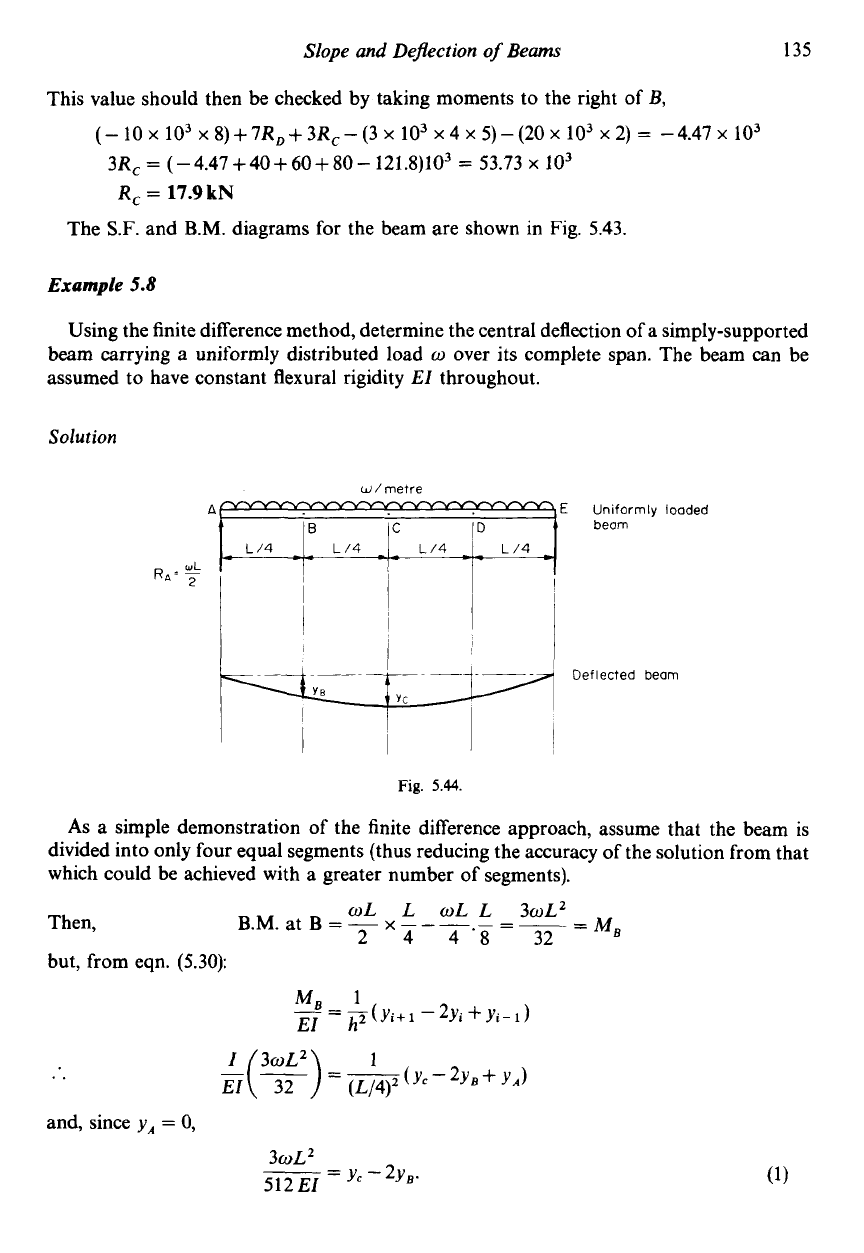
Slope
and
Defection
of
Beams
135
This value should then be checked by taking moments to the right of
B,
(
-
10
x
lo3
x
8)
+
7R,
+
3R,
-
(3
x
lo3
x
4
x
5)
-
(20
x
lo3
x
2)
=
-
4.47
x
lo3
3R,= (-4.47+40+60+80-
121.8)103
=
53.73
x
lo3
R,
=
17.9
kN
The
S.F.
and
B.M.
diagrams for the beam are shown in Fig.
5.43.
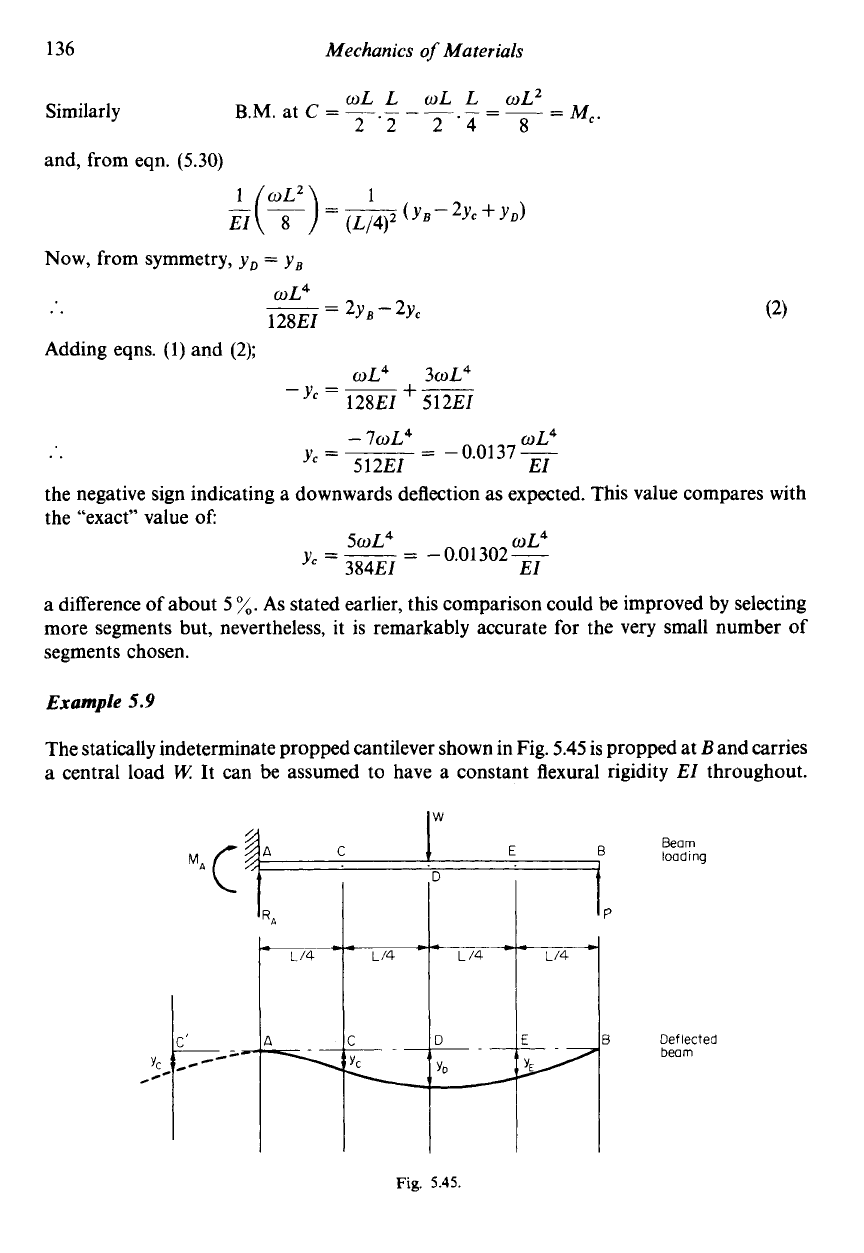
Example
5.8
Using the finite difference method, determine the central deflection of a simply-supported
over its complete span. The beam can be
beam carrying a uniformly distributed load
assumed to have constant flexural rigidity
El
throughout.
Solution
w
/
metre
A
E
Uniformly loaded
beam
Fig.
5.44.
As
a simple demonstration of the finite difference approach, assume that the beam is
divided into only four equal segments (thus reducing the accuracy of the solution from that
which could be achieved with a greater number of segments).
Then,
but, from eqn.
(5.30):
WL
L WL L 3WL2
2
4
48
32
B.M.
at
B
=
-
x
---.-
=
-
-
-
MB
and, since
y,
=
0,
3WL2
512
El
--
-
Yc
-
2YB.
136
Mechanics
of
Materials
Similarly
OL
L
OL
L
wL2
22
24
8
B.M.
at
C
=
-.-
-
--.-
=
-
- -
M,.
and, from eqn.
(5.30)
1
___
;!
(
y)
=
(L/4)2
(
YB
-
2YC
+
Y,)
Now, from symmetry,
y,
=
y,
..
wL4
128EI
--
-
2YB
-
2Yc
Adding eqns.
(1)
and
(2);
wL4
30L4
-yc=-+-
128EI 512EI
-
70L4
OL4
yc
=
~
=
-0.0137-
512EI
El
..
the negative sign indicating a downwards deflection as expected. This value compares with
the "exact" value of:
5wL4
OL4
yc=--
- -
0.01302
-
384EI
El
a difference of about
5
%.
As stated earlier, this comparison could
be
improved by selecting
more segments but, nevertheless, it is remarkably accurate for the very small number of
segments chosen.
Example
5.9
The statically indeterminate propped cantilever shown in Fig.
5.45
is propped at Band carries
a central load
W
It can be assumed to have a constant flexural rigidity
El
throughout.
Fig.
5.45

Slope
and Defection
of
Beams
137
Determine, using a finite difference approach, the values of the reaction at the prop and the
central deflection.
Solution
Whilst at first sight, perhaps, there appears to be a number of redundancies in the cantilever
loading condition, in fact the problem reduces
to
that of a single redundancy, say the
unknown prop load
P,
since with a knowledge of
P
the other “unknowns”
MA
and
R,
can be
evaluated easily.
Thus, again for simplicity, consider the beam divided into four equal segments giving three
unknown deflections
yc, y,
and
yE
(assuming zero deflection at the prop
B)
and one
redundancy. Four equations are thus required for solution and these may be obtained by
applying the difference equation at four selected points on the beam:
From eqn.
(5.30)
PL
El
B.M. at
E
=
M
=- =-
(YB-~YE
+
YO)
E
4 (L/4)2
but
y,
=
0
But
yA
=
0
..
3L
WL
El
B.M. at
C
=
Mc
=
P.-
-
-
=
-
(
Y,
-
2YC
+
YD)
4 4 (L/4)2
3PL3
m3
y,- 2yc
=
-
-
-
6464
(3)
At point
A
it is necessary to introduce the mirror image of the beam giving point
C’
to the left
of
A
with a deflection
y;
=
yc
in order to produce the fourth equation.
Then:
and again since
y,
=
0
PL3
WL3
yc=---
32
64
Solving equations
(1)
to
(4)
simultaneously gives the required prop load:
7w
P
=
=
0.318
W,
LL
and the central deflection:
(4)
17W3
wz3
y
= --=
-0.0121-
1408EI
El

138
Mechanics
of
Materials
Problems
5.1 (AD). A
beam of length 10m is symmetrically placed on two supports 7m apart. The loading is 15 kN/m
between the supports and 20kN at each end. What is the central deflection of the
beam?
E
=
210GN/mZ;
I
=
200
x 10-6m4.
[6.8 mm.]
5.2 (A/B).
Derive the expression for the maximum deflection of a simply supported
beam
of negligible weight
carrying a point load at its mid-span position. The distance between the supports is
L,
the second moment of area
of
the cross-section is
I
and the modulus of elasticity
of
the beam material is
E.
The maximum deflection of such
a
simply supported beam of length 3 m is 4.3 mm when carrying a
load
of 200 kN
at its mid-span position. What would be the deflection at the free end ofacantilever
of
the same material, length and
cross-section if it carries a load
of
l00kN at a point 1.3m from the free end?
[
13.4
mm.]
5.3 (AD). A
horizontal
beam,
simply supported at its ends, carries a load which varies uniformly from
15
kN/m
at one end to 60 kN/m at the other. Estimate the central deflection if the span is 7 m, the section 450mm deep and the
maximum bending stress 100MN/m2.
E
=
210GN/mZ.
[U.L.] [21.9mm.]
5.4
(A/B). A
beam AB,
8
m long, is freely supported
at
its ends and carries loads of 30 kN and
50
kN at points 1 m
and
5
m respectively from
A.
Find the position and magnitude of the maximum deflection.
E
=
210GN/m2;
I
=
200
x 10-6m4.
[
14.4 mm.]
5.5 (A/B). A
beam
7
m long is simply supported
at
its ends and loaded as follows: 120 kN at 1
m
from one end
A,
20 kN at 4
m
from
A
and 60 kN at
5
m from
A.
Calculate the position and magnitude of the maximum deflection. The
second moment of area of the beam section is
400
x
[9.8mm at 3.474m.l
5.6 (B). A
beam ABCD, 6 m long, is simply-supported at the right-hand end
D
and at
a
point
B
1 m from the left-
hand end A. It carries a vertical load of 10 kN at A,
a
second concentrated load of 20 kN at C, 3 m from
D,
and
a
uniformly distributed load of 10 kN/m between C and
D.
Determine the position and magnitude of the maximum
deflection if
E
=
208 GN/mZ and
1
=
35 x
C3.553 m from
A,
11.95 mm.]
5.7
(B). A
3
m long cantilever ABCis built-in at
A,
partially supported at
B,
2 m from
A,
with a force
of
10
kN and
carries
a
vertical load of 20 kN at C.
A
uniformly distributed load of
5
kN/m is also applied between
A
and
B.
Determine a) the values of the vertical reaction and built-in moment at
A
and b) the deflection of the free end C of the
cantilever.
Develop an expression for the slope of the beam at any position and hence plot a slope diagram.
E
=
208 GN/mz
and
I
=
24 x m4. [ZOkN, SOkNm, -15mm.l
5.8 (B).
Develop a general expression for the slope of the beam of question
5.6
and hence plot
a
slope diagram for
the beam. Use the slope diagram to confirm the answer given in question 5.6 for the position of the
maximum
deflection of the beam.
5.9 (B).
What would be the effect on the end deflection for question 5.7, if the built-in end
A
were replaced by a
simple support at the same position and point
B
becomes
a
full simple support position (i.e. the force at
B
is no longer
10
kN). What general observation can you make about the effect of built-in constraints on the stiffness of beams?
C5.7mm.l
5.10 (B). A
beam AB is simply supported
at
A
and
B
over a span of 3 m. It carries loads of 50kN and 40kN at
0.6m and 2m respectively from
A,
together with
a
uniformly distributed load of
60
kN/m between the 50kN and
40 kN concentrated loads. If the cross-section of the beam is such that
1
=
60
x m4 determine the value of the
deflection of the beam under the 50kN load.
E
=
210GN/m2. Sketch the S.F. and B.M. diagrams for the
beam.
13.7 mm.]
5.11 (B).
Obtain the relationship between the
B.M.,
S.F., and intensity of loading of
a
laterally loaded beam.
A
simply supported beam
of
span
L
carries a distributed load of intensity kx2/L2 where
x
is measured from one
(a) the location and magnitude of the greatest bending moment;
(b) the support reactions.
[
U.Birm.1 [0.63L, 0.0393kLZ, kL/12, kL/4.]
5.12 (B). A
uniform
beam
4m long is simplx supported at its ends, where couples are applied, each 3 kN m in
m4
determine the magnitude of the
What load must be applied at mid-span to reduce the deflection by half? C0.317 mm, 2.25 kN.]
5.13
(B).
A
500mm xJ75mmsteelbeamoflength
Smissupportedattheleft-handendandatapoint
1.6mfrom
the right-hand end.
The
beam
carries
a
uniformly distributed load of 12 kN/m on its whole length, an additional
uniformiy distributed load of 18 kN/m on the length between the supports and a point load of 30 kN at the right-
hand end. Determine the
slope
and deflection of the beam at the section midway between the supports and also at the
right-hand end.
El
for the beam is
1.5
x 10' NmZ. [U.L.] C1.13 x 3.29mm, 9.7 x 1.71 mm.]
m4 and
E
for the beam material is 210GN/m2.
m4.
support towards the other. Find
magnitude but opposite in sense.
If
E
=
210GN/m2 and
1
=
90
x
deflection at mid-span.

Slope
and
Defection
of
Beams
139
5.14
(B).
A
cantilever, 2.6 m long, carryinga uniformly distributed load
w
along the entire length, is propped at its
free end to the level of the fixed end.
If
the load on the prop is then 30 kN, calculate the value of
w.
Determine also
the
slope
of the beam at the support. If any formula
for
deflection is used it must first be proved.
E
=
210GN/m2;
I
=
4
x
10-6m4.
[U.E.I.] C30.8 kN/m, 0.014 rad.]
5.15
(B).
A
beam
ABC
of total length
L
is simply supported at one end
A
and at some point
B
along its length. It
carriesa uniformly distributed load
of
w
per unit length over its whole length. Find the optimum position
of
B
so
that
the greatest bending moment in the beam is as low
as
possible.
[U.Birm.] [L/2.]
m4, is hinged at
A
and simply
supported on a non-yielding support at
C.
The beam is subjected to the given loading (Fig. 5.46).
For
this loading
determine (a) the vertical deflection of
E;
(b) the slope of the tangent to the bent centre line at
C.
E
=
80GN/m2.
[I.Struct.E.] [27.3mm, 0.0147 rad.]
5.16
(B).
A
beam
AB,
of constant section, depth 400 mm and
I,,
=
250
x
x)
kN/rn
1”
kN
1
I
Fig. 5.46.
5.17
(B).
A
simply supported beam
AB
is 7 m long and carries a uniformly distributed load of 30 kN/m run.
A
couple is applied to the beam at a point
C,
2.5m from the left-hand end,
A,
the couple being clockwise in sense and of
magnitude 70 kNm. Calculate the slope and deflection of the beam at a point
D,
2 m from the left-hand end. Take
EI
=
5
x.
lo7 Nm’. [E.M.E.U.] C5.78
x
10-3rad, 16.5mm.l
5.18
(B).
A
uniform horizontal beam
ABC
is 0.75
m
long and is simply supported at
A
and
B,
0.5 m apart, by
supports which can resist upward or downward forces.
A
vertical load of 50N is applied at the free end
C,
which
produces a deflection of
5
mm at the centre
of
span
AB.
Determine the position and magnitude
of
the maximum
deflection in the span
AB,
and the magnitude of the deflection at
C.
.[E.I.E.] C5.12 mm (upwards), 20.1 mm.]
5.19
(B).
A
continuous beam
ABC
rests on supports at
A, B
and
C.
The portion
AB
is 2m long and carries
a
central concentrated load of40 kN, and
BC
is 3
m
long with a u.d.1. of
60
kN/m on the complete length. Draw the S.F.
and B.M. diagrams for the beam.
[
-
3.25, 148.75, 74.5 kN (Reactions);
M,
=
-
46.5
kN m.]
5.20
(B). State Clapeyron’s theorem of three moments.
A
continuous beam
ABCD
is
constructed of built-up
sections whose effective flexural rigidity
El
is constant throughout its length.
Bay
lengths are
AB
=
1
m,
BC
=
5
m,
CD
=
4 m. The beam is simply supported at
B,
C
and
D,
and carries point loads of 20 kN and 60 kN at
A
and midway
between
C
and
D
respectively, and
a
distributed load
of
30kN/m over
BC.
Determine the bending moments and
vertical reactions at the supports and sketch the B.M. and
S.F.
diagrams.
CU.Birm.1 [-20, -66.5, OkNm; 85.7, 130.93, 13.37kN.l
5.21
(B).
A
continuous beam
ABCD
is simply supported over three spans
AB
=
1 m,
BC
=
2 m and
CD
=
2 m.
The first span carries a central load
of
20 kN and the third span a uniformly distributed load of 30 kN/m. The central
span remains unloaded. Calculate the bending moments at
B
and
C
and draw the
S.F.
and B.M. diagrams. The
supports remain at the same level when the beam is loaded.
[1.36, -7.84kNm; 11.36, 4.03, 38.52, 26.08kN (Reactions).]
5.22
(B).
A
beam, simply supporded at its ends, carries a load which increases uniformly from
15
kN/m at the left-
hand end to 100 kN/m at the right-hand end. If the beam is
5
m long find the equation for the rate of loading and,
using this, the deflection
of
the beam at mid-span if
E
=
200GN/m2 and
I
=
600
x
10-6m4.
[w
=
-
(1
5
+
85x/L); 3.9 mm.]
5.23
(B).
A
beam
5
m long is firmly fixed horizontally at one end and simply supported at the other by a prop. The
beam carries
a
uniformly distributed load of 30 kN/m run over its whole length together with a concentrated load of
60 kN at a point 3 m from the fixed end. Determine:
(a) the load carried by the prop if the prop remains at the same level as the end support;
(b) the position of the point of maximum deflection.
[B.P.] [82.16kN; 2.075m.l
5.24
(B/C).
A
continuous beam
ABCDE
rests on five simple supports
A, B, C,
D
and
E.
Spans
AB
and
BC
carry a
u.d.1.
of
60 kN/m and are respectively 2 m and 3 m long.
CD
is 2.5 m long and carries a concentrated load of
50
kN at
1.5 m from
C.
DE
is 3 m long and carries a concentrated load of
50
kN at the centre and a u.d.1. of 30 kN/m. Draw the
B.M. and
S.F.
diagrams for the beam.
[Fixing moments:
0,
-44.91, -25.1, -38.95, OkNm. Reactions: 37.55, 179.1, 97.83, 118.5, 57.02kN.l

CHAPTER
6
BUILT-IN BEAMS
Summary
The
maximum bending moments and maximum deflections for built-in beams with
standard loading cases are as follows:
MAXIMUM B.M. AND DEFLECTION FOR BUILT-IN BEAMS
Loading case
Central concentrated
load W
Uniformly distributed
load w/metre
(total load
W)
Concentrated load W
not at mid-span
Distributed load w’
varying in intensity
between x
=
x, and
x
=
x2
Maximum B.M.
WL
8
-
wL2 WL
12 12
_-
--
Wab2 Wa2b
~
or
-
L2
L2
w‘(L -x)Z
MA=
-
dx
Maximum deflection
WL3
192EI
__
wL4 WL3
38481 384EI
__=-
2 Wa3b2 2aL
at x=-
(L
+
2a)
3EI(L
+
2a)2
where a
<
-
Wa3b3
3EIL3
=-
under load
140

$6.1
Built-in Beams
141
Efect
of
movement
of
supports
If one end
B
of an initially horizontal built-in beam
AB
moves through a distance
6
relative
to end
A,
end moments are set up of value
and the reactions at each support are
Thus, in most practical situations where loaded beams sink at the supports the above values
represent
changes
in fixing moment and reaction values, their directions being indicated in
Fig. 6.6.
Introduction
When both ends of
a
beam are rigidly fixed the beam is said to be
built-in, encastred
or
encastri.
Such beams are normally treated by a modified form of Mohr’s area-moment
method or by Macaulay’s method.
Built-in beams are assumed to have zero slope at each end,
so
that the total change of slope
along the span is zero. Thus, from Mohr’s first theorem,
M.
El
area of
-
diagram across the span
=
0
or, if the beam is uniform,
El
is constant, and
area
of
B.M. diagram
=
0
(6.1)
Similarly, if both ends are level the deflection of one end relative to the other is zero.
Therefore, from Mohr’s second theorem:
M
EI
first moment of area of
-
diagram about one end
=
0
and, if
EZ
is constant,
first moment
of
area
of
B.M. diagram about one end
=
0
(6.2)
To make use of these equations it is convenient to break down the B.M. diagram for the
(a) that resulting from the loading, assuming simply supported ends, and known as the
(b) that resulting from the end moments or fixing moments which must
be
applied at the
built-in beam into two parts:
free-moment diagram;
ends to keep the slopes zero and termed the
fixing-moment diagram.
6.1.
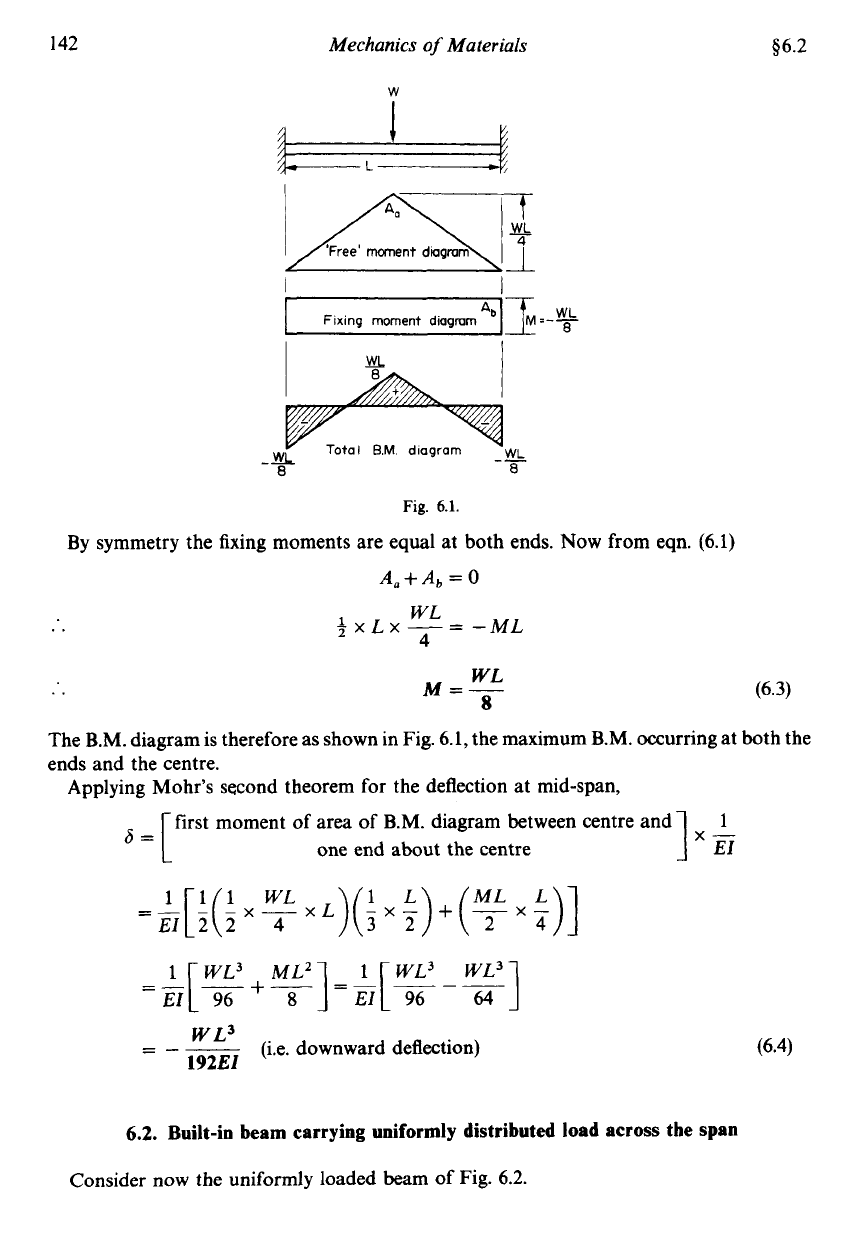
Built-in beam carrying central concentrated load
Consider the centrally loaded built-in beam of Fig. 6.1.
A,
is the area of the free-moment
diagram and
A,
that of the fixing-moment diagram.
142
Mechanics
of
Materials
46.2
iA-
Free' ment diagram
Fixing moment diagmm
%I1
M=-%
8
Fig.
6.1.
By symmetry the fixing moments are equal at both ends. Now from eqn.
(6.1)
A,+&
=
0
..
WL
3
x
LX
-=
-ML
4
The B.M. diagram is therefore as shown in Fig.
6.1,
the maximum B.M. occurring at both the
ends and the centre.
Applying Mohr's second theorem for the deflection at mid-span,
first moment
of
area
of
B.M. diagram between centre and
one end about the centre
6=[
1L ML L
1
[
WL~
ML~
1
WL~ WL~
EZ
96
8
El
96
(i.e. downward deflection)
WLJ
192EZ
-
--
-
6.2.
Built-in beam carrying uniformly distributed load across the span
Consider now the uniformly loaded beam of Fig.
6.2.
