Hearn E.J. Mechanics of Materials. Volume 1
Подождите немного. Документ загружается.

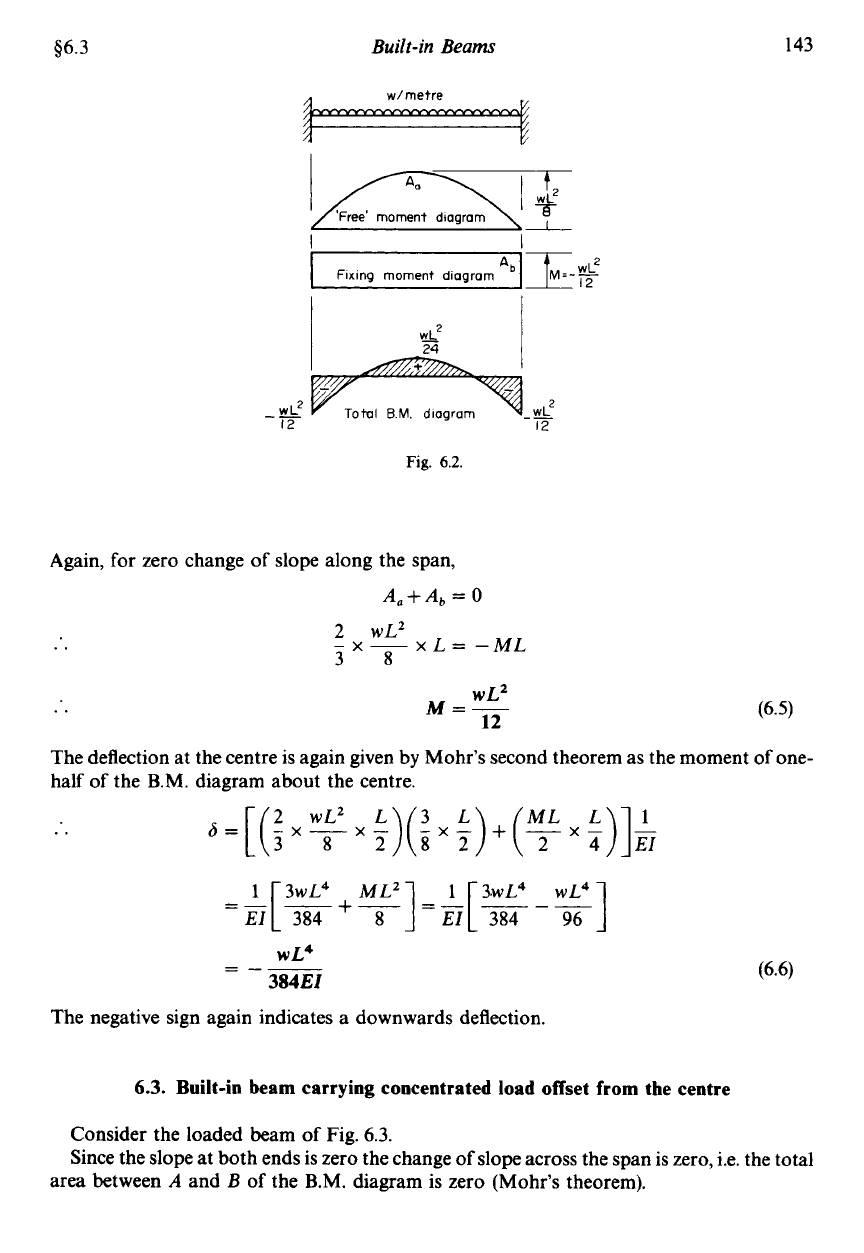
$6.3
Built-in
Beams
143
'Free' moment diagram
I
I
Fixing moment diagram
Ab1Z-d
12
I
I
Fig.
6.2.
Again, for zero change of slope along the span,
&+A,
=
0
..
2
WL2
-x- xL=-ML
38
The deflection at the centre is again given by Mohr's second theorem as the moment of one-
half of the B.M. diagram about the centre.
..
6
=
[
(3
x
$
x
;)(;
x
;)+
(y
x
$)]A
EI
wL4
384
E
I
The negative sign again indicates a downwards deflection.
-
-
--
6.3.
Built-in beam carrying concentrated load offset from the centre
Consider the loaded beam of Fig.
6.3.
Since the slope at both ends is zero the change
of
slope across the span is zero, i.e. the total
area between
A
and
B
of
the B.M. diagram is zero (Mohr's theorem).

144
Mechanics
of
Materials
46.3
..
L
Fig.
6.3.
Also
the deflection of
A
relative to
B
is zero; therefore the moment
of
the
B.M.
diagram
between
A
and
B
about
A
is
zero.
...
[~x~xa]~+[jxt wabxb
I(
a+-
:)
+
(
+MALx-
4)
+
(
+MBLx-
't)
=O
Wab
MA+2M~=
-
---[2a2+3ab+b2]
L3
Subtracting
(l),
Wab
L3
M
-
-
-[2a2
+
3ab+ b2
-
L2]
8-
but
L=a+b,
Wab
L3
M
[2a2
+
3ab
+
bZ
-
a2
-
2ab
-
b2]
B-
..
Wab Wa'bL
[a
+ab]
=
-___
L3 L3
=
-__
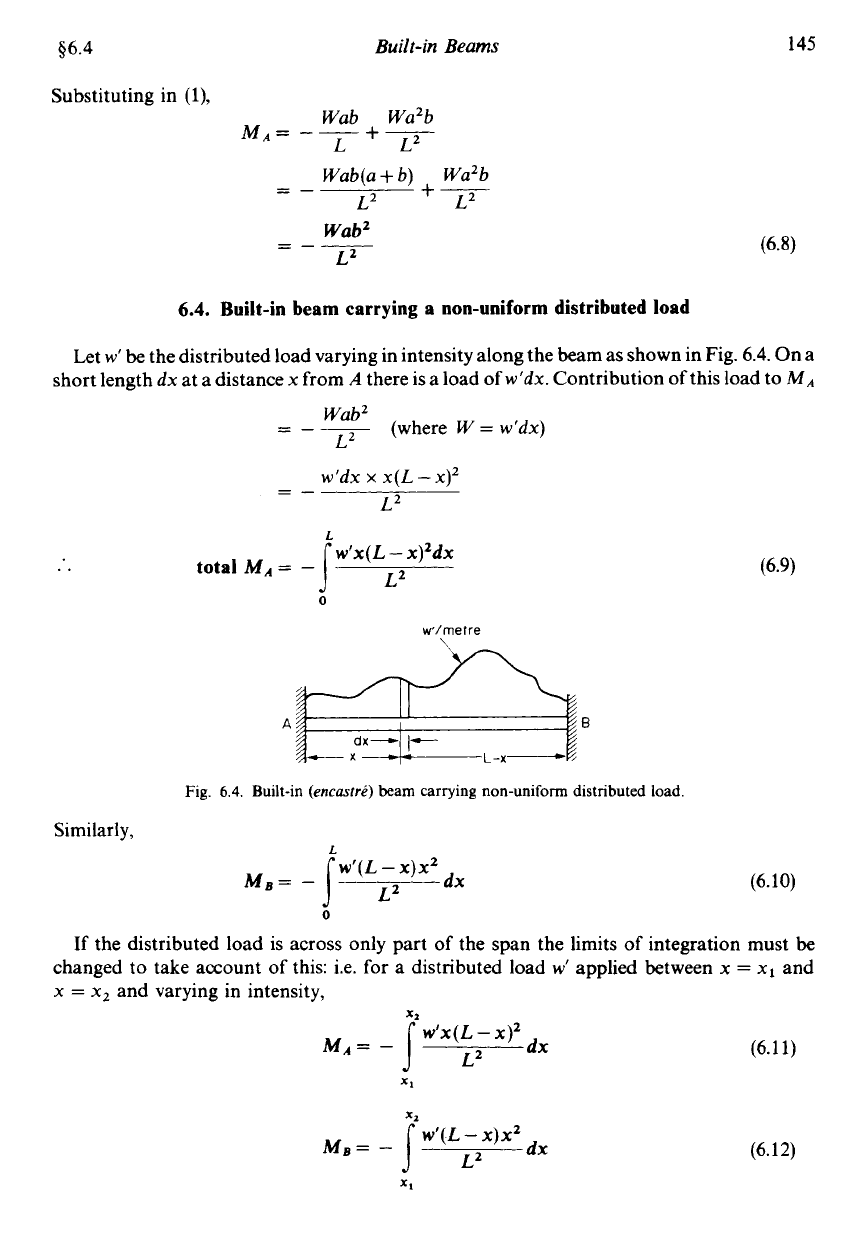
56.4
Built-in Beams
145
Substituting in (l),
Wab Wa2b
L
L2
M
---+-
A-
Wab(a
+
b) Wa2b
=-
+-
Wab’
LZ
L2
L2
=
-__
6.4.
Built-in beam carrying a non-uniform distributed load
Let
w’
be
the distributed load varying in intensity along the beam as shown in Fig. 6.4. On a
short length
dx
at a distance
x
from
A
there is a load of
w’dx.
Contribution
of
this load to
MA
Wab2
=
-~
L2
(where
W
=
w’dx)
w’dx
x
x(L
-
x)’
L2
1
w’x( L;x)’dx
-
--
total
MA
=
-
0
w’/me
tre
\
Fig.
6.4. Built-in
(encostre)
beam carrying non-uniform distributed load
Similarly,
(6.9)
(6.10)
0
If the distributed load is across only part
of
the span the limits
of
integration must
be
changed to take account
of
this: i.e. for a distributed load
w’
applied between
x
=
xl
and
x
=
x2
and varying in intensity,
(6.1 1)
(6.12)

146
Mechanics
of
Materials
$6.5
6.5.
Advantages and disadvantages
of
built-in beams
Provided that perfect end fixing can
be
achieved, built-in beams carry smaller maximum
B.M.s (and hence are subjected to smaller maximum stresses) and have smaller deflections
than the corresponding simply supported beams with the same loads applied; in other words
built-in beams are stronger and stiffer. Although this would seem to imply that built-in beams
should be used whenever possible, in fact this is not the case in practice. The principal reasons
are as follows:
(1)
The need for high accuracy in aligning the supports and fixing the ends during erection
(2)
Small subsidence of either support can set up large stresses.
(3)
Changes of temperature can also set up large stresses.
(4)
The end fixings are normally sensitive to vibrations and fluctuations in B.M.s, as in
These disadvantages can be reduced, however, if hinged joints are used at points on the
beam where the B.M. is zero, i.e. at
points
of
inflexion
or
contraflexure.
The beam is then
effectively a central beam supported on two end cantilevers, and for this reason the
construction is sometimes termed the
double-cantilever
construction. The beam
is
then free to
adjust to changes in level of the supports and changes in temperature (Fig.
6.5).
increases the cost.
applications introducing rolling loads (e.g. bridges, etc.).
oints
of
inflexion
Fig.
6.5.
Built-in
beam
using “doubleantilever” construction.
6.6.
Effect
of
movement
of
supports
Consider a beam
AB
initially unloaded with its ends at the same level. If the slope is to
remain horizontal at each end when
B
moves through a distance
6
relative to end
A,
the
moments must be as shown in Fig.
6.6.
Taking moments about
B
RA
x
L
=
MA+ MB
MA= Mg= M
and, by symmetry,
2M
L
..
RA=-
Similarly,
2M
L
RB=-
in the direction shown.
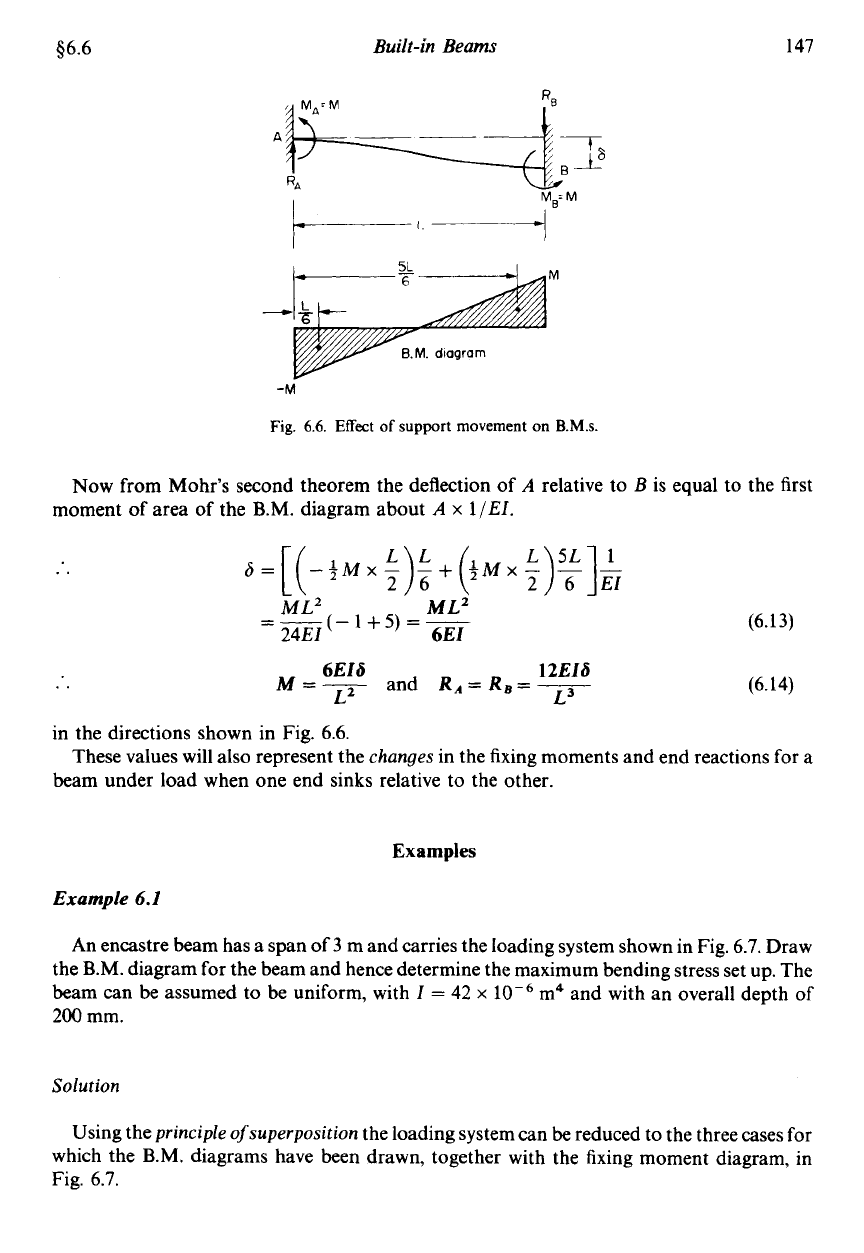
$6.6
Built-in
Beams
147
-M
Fig.
6.6.
Effect
of
support
movement
on
B.M.s.
Now from Mohr’s second theorem the deflection of
A
relative to
B
is equal to the first
moment
of
area of the B.M. diagram about
A
x
l/EI.
..
12EIS
and
RA=Re=-
6E1S
M=---
L2
L3
(6.14)
in the directions shown in Fig.
6.6.
beam under load when one end sinks relative to the other.
These values will
also
represent the
changes
in the fixing moments and end reactions for
a
Examples
Example
6.1
An encastre beam has a span
of
3
m and carries the loading system shown in Fig.
6.7.
Draw
the B.M. diagram
for
the beam and hence determine the maximum bending stress set up. The
beam can be assumed to be uniform, with
I
=
42
x
m4 and with an overall depth
of
200
mm.
Solution
Using the
principle ofsuperposition
the loading system can
be
reduced to the three cases for
which the
B.M.
diagrams have been drawn, together with the fixing moment diagram, in
Fig.
6.7.
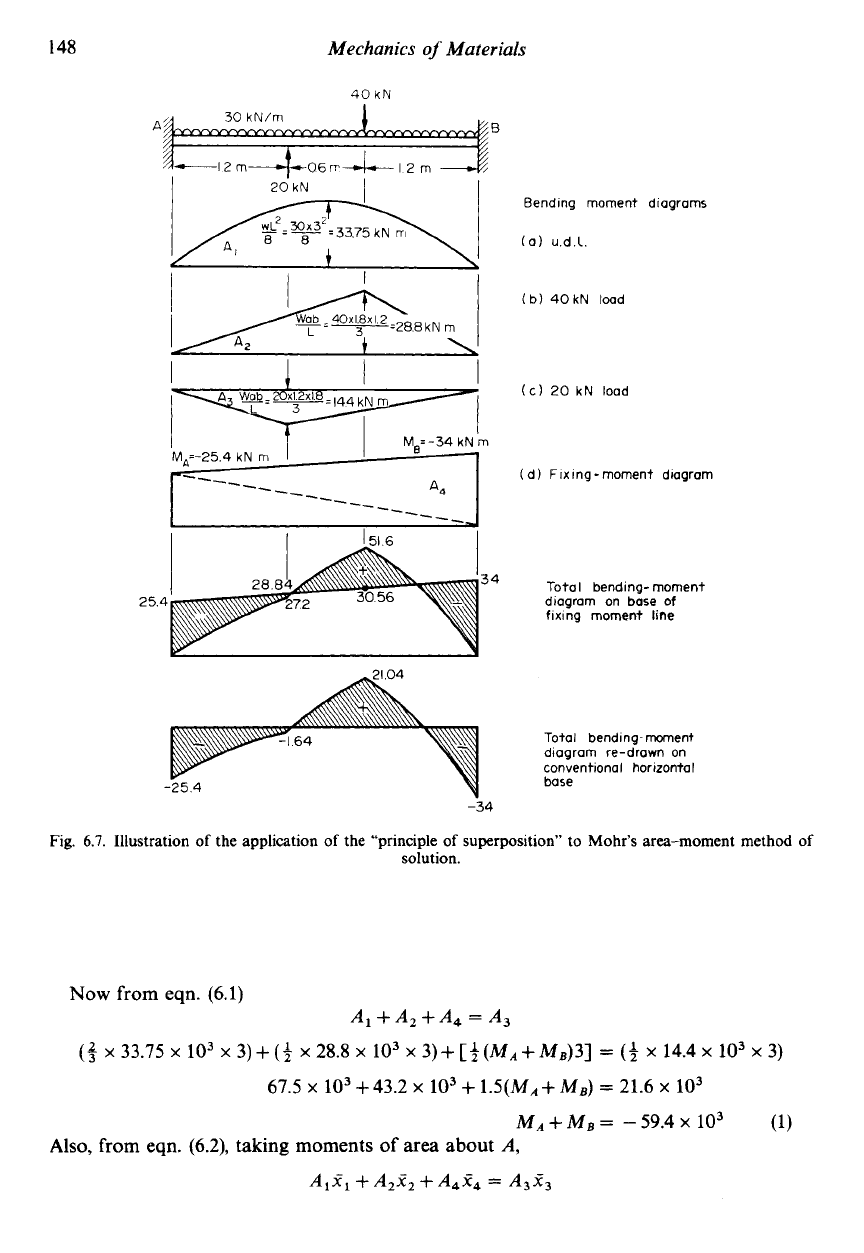
148
Mechanics
of
Materials
40
kN
A
0
20
kN
I
I
1
I
M,=
-34
kN
rn
M,=-25.4
kN
rn
I
---_
--
--
---
--
Bending moment diagrams
(a) u.d.1.
(b) 40kN load
(c)
20
kN load
(d) Fixing-moment diagram
Total bending- moment
diagram on
base
of
fixing moment line
Total bending-moment
diagram re-drawn on
conventiona
I
horizonta
I
base
-34
Fig.
6.7.
Illustration
of
the application
of
the “principle
of
superposition” to Mohr’s area-moment method
of
solution.
Now
from
eqn.
(6.1)
A1
+
A2
+
A4
=
A3
(~X33.75X103x3)+(~
~28.8~10~X3)+[$(MA+M~)3]=(~~14.4~10~~3)
67.5
x
lo3
+43.2
x
lo3
+
1.5(MA
+
MB)
=
21.6
x
lo3
MA
+
MB
=
-
59.4
x
103
(1)
Also,
from
eqn.
(6.2),
taking moments
of
area about
A,
A121
+
A222
+
A424
=
A323

Built-in
Beams
149
and, dividing areas
A,
and
A,
into the convenient triangles shown,
2
x
1.8
3
(67.5
x
IO3
x
1.5)+
(3
x
28.8
x
lo3
x
1.8)-
+
(5
x
28.8
x
lo3
x
1.2)(1.8+
$
X
1.2)
+
(3
MA
x
3
x
$
x
3)
+
(f
MB
x
3
x
5
x
3)
=
(4
x
14.4
x
lo3
x
12)3
x
1.2
+
(f
x
14.4
x
lo3
x
1.8) 1.2
+
-
(
Y)
(101.25
+
31.1
+
38.0)103
+
1.5MA+ 3MB
=
(6.92
+
23.3)103
1.5 MA+ 3MB
=
-
140
X
lo3
MA
+
2MB
=
-
93.4
x
lo3
(2)
MB= -34x103Nm= -34kNm
and from (l),
The fixing moments are therefore negative and not positive as assumed in Fig. 6.7. The total
B.M.
diagram is then found by combining all the separate loading diagrams and the fixing
moment diagram to produce the result shown in Fig. 6.7. It will
be
seen that the maximum
B.M. occurs at the built-in end
B
and has a value of 34kNm. This will therefore be the
position
of
the maximum bending stress also, the value being determined from the simple
bending theory
MA= -25.4~ 103Nm
=
-25.4kNm
MY
34
x
103
x
io0
x
10-3
omax=
-
-
-
I
42
x
=
81
x
lo6
=
81
MN/mZ
Example
6.2
A
built-in beam, 4 m long, carries combined uniformly distributed and concentrated loads
as shown in Fig. 6.8. Determine the end reactions, the fixing moments at the built-in supports
and the magnitude of the deflection under the 40 kN load. Take
El
=
14 MN m2.
30
kN/m
40
kN
I
X
Fig.
6.8.
Solution
Using Macaulay's method (see page 106)

150
Mechanics
of
Materials
Note that the unit
of
load
of
kilonewton is conveniently accounted
for
by dividing
EZ
by
lo3. It
can then be assumed in further calculation that RA
is
in kN and MA in kNm.
Integrating,
_-
EI
dy
=
M,x+RA---[(~-1.6)~]--[(~-1.6)~]
x2
40 30
+A
lo3
dx
22 6
and
EI
x2
x3
40
30
2 66 24
my
=
MA-
+
RA-
-
-[
(x-
1.6y]
-
-[(x-
1.6)4]
+AX
+B
Now, when
x
=0,
y=O
...
B=O
dY
and whenx=O,
-
=O
.’.
A
=O
dx
When
x
=4,
y
=O
42 43 40 30
2 66 24
0
=
MA
X
-
+
RA
x
-
-
-
(2.4)3
-
-
(2.4)4
0
=
8MA+ 10.67 RA-92.16-41.47
133.6
=
8MA+ 10.67 RA
N
lq
’
dY
When
x
=
4,
-
=O
dx
42
40
30
2 2 6
0
=
MA+
-RA- -(2.4)’- -(2.4)3
Multiply (2)
x
2,
(3)
-
(I),
Now
..
368.64
=
8MA
+
16RA
=
44.1
kN
235.04
5.33
RA=-
RA+RB
=
40-t
(2.4
X
30)
=
112kN
RB
=
112 -44.1
=
67.9
kN
Substituting in (2),
4MA+ 352.8
=
184.32
..
MA
=
(184.32
-
352.8)
=
-
42.12
kN
m
i.e. MA is in the opposite direction to that assumed in Fig. 6.8.

Built-in
Beams
151
Taking moments about
A,
MB+4RB-(40X
1.6)-(30~2.4~2.8)-(-42.12)=0
..
i.e. again in the opposite direction to that assumed in Fig.
6.8.
(Alternatively, and more conveniently, this value could have been obtained by substitution
into the original Macaulay expression with
x
=
4,
which
is,
in effect, taking moments about
B.
The need to take additional moments about
A
is then overcome.)
MB
=
-
(67.9
x
4)
+
64
+
201.6
-
42.12
=
-
48.12
kN
m
Substituting into the Macaulay deflection expression,
xz
44.12 20
GYy
2 6
3
=
-42.1-
+
~
-
-
[X
-
1.613
-
$[x
-
1.614
El
Thus, under the
40
kN load, where
x
=
1.6
(and neglecting negative Macaulay terms),
-
(42.1
x
2.56)
(44.1
x
4.1)
y
=E[
EZ
2
+
6
-0-01
23.75 x
lo3
14 x
lo6
=- =
-1.7~
10+m
=
-
1.7mm
The negative sign as usual indicates
a
deflection downwards.
Example
6.3
Determine the fixing moment at the left-hand end of the beam shown in Fig.
6.9
when the
load varies linearly from
30
kN/m to
60
kN/m along the span
of
4
m.
30
kNhI
kN/rn
A
Fig.
6.9.
Solution
From
$6.4
Now
w'
=
(30
+
F)
lo3
=
(30
+
7.5x)103
N/m

152
Mechanics
of
Materials
..
MA
=
-
/
(30
+
7.5x)103 (4
-
x)~
x
dx
42
0
4
103
- - -
-
J
(30
+
7.5~)(16
-
8x
+
x2)x
dx
16
0
4
103
=
-
-
1
(480~
-
2402
+
30x3
+
1202
-
60x3
+
7.5~~)
dx
16
0
4
103
-
- -
-
1
(480~
-
120x2
-
30x3
+
7.5x4)dx
16
0
103
=
--[240~16-40~64-30~64+2.5~1024]
16
=
-120x103Nm
The required moment at
A
is thus
120
kN
m in the opposite direction to that shown in
Fig. 6.8.
Problems
6.1
(A/B). A
straight beam
ABCD
is rigidly built-in at
A
and
D
and carries point loads of
5
kN at
B
and
C.
AB
=
BC =CD
=
1.8m
If
the second moment of area
of
the section
is
7
x
10-6m4 and
Young’s
modulus is 210GN/mZ, calculate:
(a) the end moments;
(b)
the central deflection of the beam.
[U.Birm.l[-6kNm; 4.13mm.l
6.2
(A/B). A
beam of uniform section with rigidly
fixed
ends which are at the same level has an effective
span
of
10 m. It carries loads
of
30 kN and
50
kN at 3 m and 6 m respectively from the left-hand end. Find the vertical
reactions and the fixing moments at each end of the beam. Determine the bending moments at the two points
of
loading and sketch, approximately to scale, the
B.M.
diagram for the beam.
c41.12, 38.88kN; -92,
-90.9,
31.26, 64.62kNm.l
6.3
(A/B). A
beam
of
uniform section and of 7 m
span
is “fixed” horizontally at the same level at each end. It
carries a concentrated load
of
100 kN at 4m from the left-hand end. Neglecting the weight of the
beam
and working
from first principles, find the position and magnitude of the maximum deflection if
E
=
210GN/m2 and
I
=
1%
x
m4. C3.73 from
1.h.
end; 4.28mm.l
6.4
(A/B). A
uniform beam, built-in at each end, is divided into four equal parts and has equal point loads, each
W,
placed at the centre of each portion. Find the deflection at the centre of this beam and prove that it equals the
deflection at the centre of the same beam when carrying an equal total load uniformly distributed along the entire
length.
[U.C.L.I.]
[--.I
WL’
96~1
