Heard D.E. (editor) Analytical Techniques for Atmospheric Measurement
Подождите немного. Документ загружается.

Chapter 2
Infrared Absorption Spectroscopy
Alan Fried and Dirk Richter
2.1 Introduction
Absorption spectroscopy is the study of the absorption of electromagnetic radiation by
atoms and molecules. In this approach, one measures the absorbed light intensity as
a function of wavelength. Spectroscopic data can be used to study molecular structure
such as the size, shape and nature of the absorbing molecules as well as the nature of
the chemical bonds and the interactions among energy levels involved in the transi-
tions. Since different molecules absorb electromagnetic radiation at different specific
wavelengths, absorption spectroscopy has also found wide-ranging applications as a tool
for measuring trace concentrations of various molecules in (1) laboratory-based kinetic
and mechanistic studies, (2) combustion studies, (3) medical applications, (4) automotive
studies, (5) cigarette emission studies, (6) studies of flux to and from various surfaces,
(7) detection of explosives and bio-agents, and (8) measurements of trace atmospheric
constituents for atmospheric studies, to name a few.
This chapter will focus on the last application, with specific emphasis on measurements
employing electromagnetic radiation in the infrared (IR) spectral region. Such measure-
ments are critical for understanding a number of important atmospheric processes,
including the build-up of greenhouse gases and their role in future climatic change as well
as detailed mechanistic information regarding chemical processing in the atmosphere,
to name a few examples. With the exception of noble gases and homonuclear diatomic
molecules such as O
2
,N
2
, and H
2
, nearly all atmospheric constituents exhibit moderate
to strong absorptions in the IR, making IR absorption spectroscopy an extremely versatile
tool for atmospheric studies. Although liquid and solid aerosols have been shown to play
major roles in atmospheric chemistry, this chapter will only focus on IR absorption from
gas-phase molecular species. Techniques employing absorption of radiation in the ultra-
violet (UV) and visible regions of the electromagnetic spectrum, which are also valuable
tools for atmospheric research, will be discussed in Chapter 3. Approaches involving
measurements of the subsequent re-emission of the absorbed energy in the form of
fluorescence will be discussed in Chapter 4.
This chapter will introduce many of the important concepts commonly used in
absorption spectroscopy, including the fundamentals of electromagnetic radiation and its
interaction with molecules, absorption cross-sections and selection rules, Beer–Lambert
law, vibrational bands, vibrational-rotational features, lineshapes, as well as many other
Infrared Absorption Spectroscopy 73
basic concepts. The important fundamental mathematical formulations will be presented
along with information regarding how such expressions can be derived and the under-
lying assumptions. However, in no case do we endeavor to present rigorous derivations
or rigorous quantum theory, both of which can be found in numerous textbooks (see
‘Further reading’ in the ‘Reference’ section). Many of the details regarding rotational and
vibrational energy levels and the various interactions will also not be presented. Instead,
the focus is on the important conclusions and inferences that one should extract from the
expressions that are presented. After discussing the fundamental theory, we will highlight
the types of IR absorption approaches that have commonly been employed to study trace
atmospheric constituents approximately since 1990 as well as the specific atmospheric
gases that have been studied. The strengths and weaknesses of these measurements
will be discussed and, wherever possible, comparisons with other approaches and other
wavelength regions will be given. This chapter will employ SI units wherever possible.
However, in many cases expressions and important variables are denoted in the cgs system
of units, and this chapter will adopt this philosophy when these expressions are presented.
2.2 Fundamentals of infrared absorption spectroscopy
2.2.1 Electromagnetic radiation in the infrared
We first present some of the fundamentals related to the terms used throughout this
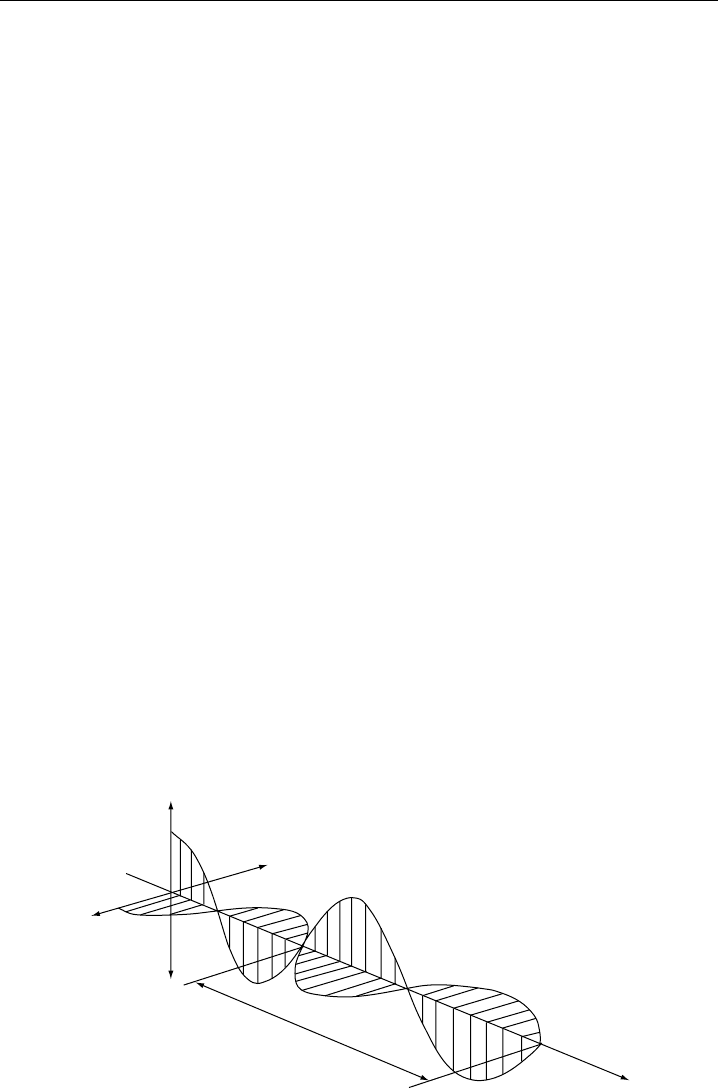
chapter. All electromagnetic radiation is classified in terms of its wavelength. Figure 2.1
depicts a classical electromagnetic wave with orthogonal electric and magnetic fields, both
of which are orthogonal to the direction of light propagation. The distance between the
wave peaks is the wavelength and is denoted by , while the number of waves per unit
time is the frequency in units of cycles per second or Hertz. These parameters are
E
M
One wavelength (
λ)
y
z
x
Figure 2.1 Electromagnetic wave with orthogonal electric and magnetic fields.

74 Analytical Techniques for Atmospheric Measurement
related through the speed of light in vacuum cc=299792×10
8
ms
−1
by the following
relationship:
= c/ (2.1)
The energy E of a photon for this wave can be expressed in terms of this frequency via
a proportionality constant, h (where h = 6626 ×10
−34
J s), known as Planck’s constant:
E = h (2.2)
It is important to note that applications for each spectral region of the electromagnetic
spectrum have developed independent of one another, and hence each spectral region has
acquired its own preferred set of units. In the IR spectral region, the units of wavelength
are frequently given in terms of m10
−6
m and nm 10
−9
m. In the mid-IR spectral
region (to be defined shortly) one almost exclusively works in units of wave numbers,
,
which is the reciprocal of the wavelength in cm and has units of cm
−1
:
= 1/ cm
−1
(2.3a)
and thus,
E = h =hc/ =h
c (2.3b)
A wavelength of 1 m is 1000 nm, 10 000 Å 1 ×10
−4
cm, and 10 000 cm
−1
.
The parameters of wavelength and wave numbers in all the above expressions refer to
vacuum, whereas most fundamental spectroscopic measurements employ a spectrometer
operated in a non-vacuum environment. The wavelength in air
air
is related to the
wavelength in vacuum by the refractive index n via:
vac
= n
air
=
air
+n −1
air
(2.3c)
At IR wavelengths in the 1–16 m range considered in this chapter, the term n −1
takes on values around 273×10
−4
for standard air (dry air at 15
C at 1 atm pressure and
0.03% CO
2
). Values for other conditions are given by Coleman et al. (1960). In trace
atmospheric measurements the distinction between vacuum and air is automatically dealt
with, since one typically compares their observed spectrum to reference spectra given in
vacuum units.
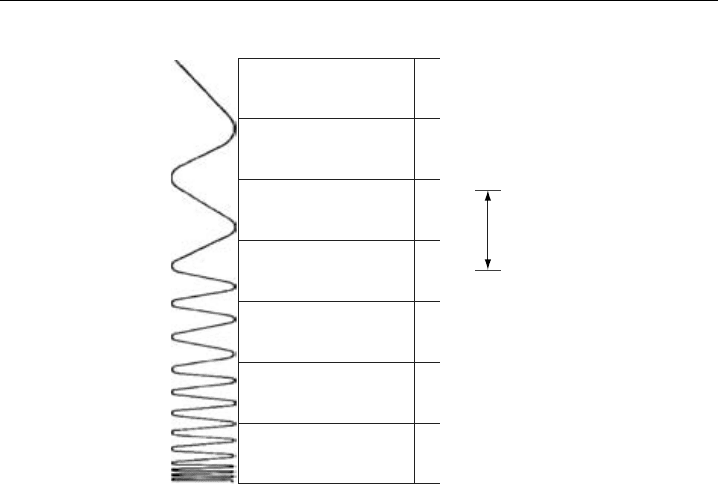
Figure 2.2 depicts the different regions of the electromagnetic spectrum employed in
atmospheric studies, which extends from the vacuum UV to the microwave spectral
regions. It is important to note that the exact delineations between spectral regions are
approximate and differ somewhat from reference to reference. As shown, the IR spectral
region spans the approximate wavelength range from the end of the visible region at
07 m to the start of the microwave region at 500 m. It will be more useful for the
discussions of this chapter to further characterize the IR spectral region in terms of three
sub-regions, where again the exact delineations vary somewhat from text to text. These
three regions are: (1) the near-IR, which extends from approximately 0.7 to 25 m;
(2) the mid-IR, which extends from 2.5 to 25 m; and (3) the far-IR, which extends from
Infrared Absorption Spectroscopy 75
Vacuum ultra-violet
Microwave
Ultra-violet
Visible
Near infrared
Mid-infrared
Far-infrared
500
μm
10
cm
0.7
μm
2.5
μm
25
μm
0.4
μm
10
nm
100
nm
16 μm
1
μm
Figure 2.2 Regions of the electromagnetic spectrum with approximate wavelength delineations on the
right-hand axis.
25 to 500 m. This chapter will only consider the 1–16 m spectral region where most
IR studies of atmospheric constituents tend to focus.
The near- and mid-IR spectral regions are distinguished from other spectral regions
not only by wavelength but also by the nature of the molecular interactions involved, the
sheer number of gas-phase atmospheric constituents exhibiting absorption features, and
the characteristics of the recorded spectra in terms of absorption strengths and linewidths.
We will examine each of these aspects in further detail in the following sections.
2.2.2 Molecular interactions in the IR
When electromagnetic radiation is incident upon a molecule, the oscillating electric field,
shown in Figure 2.1, under the right set of conditions, interacts with the dipole moment
of the molecule to produce a change in energy of the molecule from some lower state
with energy E
1
to an upper state with energy E
2
. One can find a detailed mathematical
treatment of such a system in most books on quantum mechanics and spectroscopy,
and two such excellent references are Barrow (1962) and Levine (1970). In these and
most references, one treats the molecule quantum-mechanically and the radiation field
as a classical wave employing time-dependent perturbation theory. Considering only the
interactions involving the electric field, since the magnetic force is much smaller, one
arrives at an expression for the probability of a transition that is proportional to the
square of the product of three terms: the maximum amplitude of the electric field E
0
,
the transition moment
12
, and an expression that contains two fractions – one term

76 Analytical Techniques for Atmospheric Measurement
that becomes important for absorption and the other term that becomes important for
stimulated emission. Considering only absorption from state 1 to state 2, the second
fraction drops out and the transition probability is proportional to:
E
0
12
1 −e
2i/hE−ht
E −h
2
(2.4)
The term E represents the difference in energy between the two molecular energy levels
E = E
2
−E
1
and h represents the photon energy from Equation 2.2. The transition
moment is given by:
12
=
2
∗
1
d (2.5)
Here,
1
and
2
represent the wavefunctions for the two energy levels, and is the
dipole moment operator along a specific direction of the electric field. One can write
Expressions 2.4 and 2.5 for each of the x y, and z components of the electric field. The
dipole moment operator for a distribution of i charges is determined from the summation
of the product of the electric field charge q
i
times a position vector:
= i
i
q
i
x
i
+j
i
q
i
y
i
+k
i
q
i
z
i
(2.6)
The terms i j, and k represent unit vectors in the x y, and z directions and the terms
x
i
, y
i
, and z
i
are the Cartesian coordinates in these directions.
Equation 2.4 contains the important result that in order for a electric-dipole moment–
allowed transition allowed by the electric-dipole moment to be non-negligible, each of
the three terms must be non-zero. One obtains a non-negligible value for the fractional
term in the bracket only when the energy difference between the two energy levels is
equal to the photon energy, namely E = h. In this case the denominator approaches
zero and the quotient becomes large but not infinite. Under these circumstances, the
square of the transition moment, in equation 2.5, determines the magnitude of the
electric dipole–allowed absorption strength for a given field strength. Since only certain
molecular transitions will result in non-zero transition moments, spectroscopists devise
selection rules to determine which transitions are allowed. However, this analysis only
refers to electric dipole–allowed transitions, and electric quadrupole transitions orders of
magnitude weaker may still occur.
Absorption of electromagnetic radiation in the IR spectral region, with a few exceptions,
involves interactions with molecular vibrations and rotations. The resulting absorption
spectra involve transitions between rotational levels of some lower vibrational state
(generally the ground vibrational level) and rotational levels of some higher vibrational
state. For this reason these transitions are referred to as vibrational-rotational transitions.
In order for such transitions to occur, the square of the transition moment expression
of equation 2.5 using vibrational wavefunctions must be non-zero. One can further
determine conditions for IR transitions by examining the variation of the dipole moment
during a vibration. This is accomplished by expanding each of the dipole-moment
Cartesian coordinates in terms of normal coordinates Q
i
,a3N coordinate system
(where N is the number of atoms in the molecule) that translates and rotates with the

Infrared Absorption Spectroscopy 77
molecule. For small vibrational displacements, the transition moment of equation 2.5
becomes the sum of two terms, one involving the permanent dipole moment in the
equilibrium position
0
and the other involving the summation for the derivative of
the dipole moment as a function of each of the i normal coordinates:
12
=
0
2
∗
1
d +
i
Q
i
0
2
∗
Q
i
1
(2.7)
The first integral vanishes since the vibrational wavefunctions are orthogonal to each
other for different vibrational states. The second term, which represents the transition
moment for vibrational transitions, is non-zero only when the dipole moment derivative
in front of the integral is non-zero. A change in either the magnitude or direction of the
dipole moment will satisfy this criterion. Since noble gases and homonuclear diatomic
molecules such as O
2
,N
2
, and H
2
do not satisfy this condition, they do not possess
allowed IR transitions. In addition, many vibrational modes of polyatomic molecules are
also absent because this condition is not satisfied. However, N
2
exhibits weak quadrupole
transitions in the 38–50 m spectral range, with integrated line intensities 6–15 orders
of magnitude weaker than typical trace gases of atmospheric interest.
2.2.3 Vibrational bands and rotational lines in the IR
Having assessed the general conditions necessary for IR absorption, we now further
examine vibrational-rotational spectral features and their general properties. As in the
previous section, we present only a very brief overview, which is necessary for subsequent
discussions of trace gas detection employing IR absorption spectroscopy. More detailed
treatments of this subject can be found in classic textbooks such as Herzberg (1945) and
King (1964), and in books by Banwell and McCash (1994) and Duxbury (2000).
An IR absorption spectrum consists of a series of bands due to transitions where
the vibrational quantum number changes in the ground electronic state. Under higher
resolution one observes a series of closely spaced absorption lines within each vibrational
band due to simultaneous changes in the rotational quantum number. In the case of
diatomic molecules there is only one vibrational mode, which can take on various
vibrational quantum numbers. Dipole moment–allowed selection rules indicate that the
change in rotational quantum number J may take on values of ±1, and in certain
electronic states a value of 0. Rotational lines where J =+1 during the transition from
the ground to the excited vibrational state are designated R-branch lines, and where
J =−1, as P-branch lines. Q-branch lines occur when J = 0, and result in a series of
closely spaced lines near the band origin
0
, the transition frequency in cm
−1
between the
two vibrational levels in the absence of rotation. In the absence of centrifugal distortion
(a changing internuclear distance as the molecule vibrates) and other interactions, one
may write the following simple general expression for the frequencies of such rotational
lines:
12
=
0
+B
v
J
J
+1 −B
v
J
J
+1 (2.8)

78 Analytical Techniques for Atmospheric Measurement
Here, B
v
and B
v
are the rotational constants in the upper and lower vibrational states,
respectively (where B is proportional to the inverse of the square of internuclear distance),
while J
and J
represent the rotational quantum numbers of these states.
Like diatomic molecules, there is one principal moment of inertia in linear polyatomic
molecules, and thus rotational spectra can be described by Equation 2.8 for the vibrational
mode (to be discussed) under consideration. There are, however, subtle differences
between diatomic and linear polyatomic spectra. In linear polyatomic molecules, like CO
2
,
the two bending vibrations (to be discussed) are degenerate, resulting in the presence
of l-doubling of the vibrational levels. A second difference relates to differences in the
statistical weights, factors that give the multiplicity of the rotational energy levels. Finally,
as the rotational B values for polyatomic molecules are significantly smaller than diatomics
due to the increased mass (by one or more orders of magnitude), the rotational features
of polyatomic molecules are closer in spacing than diatomics. Generally as the molecule
gets larger the rotational features become denser.
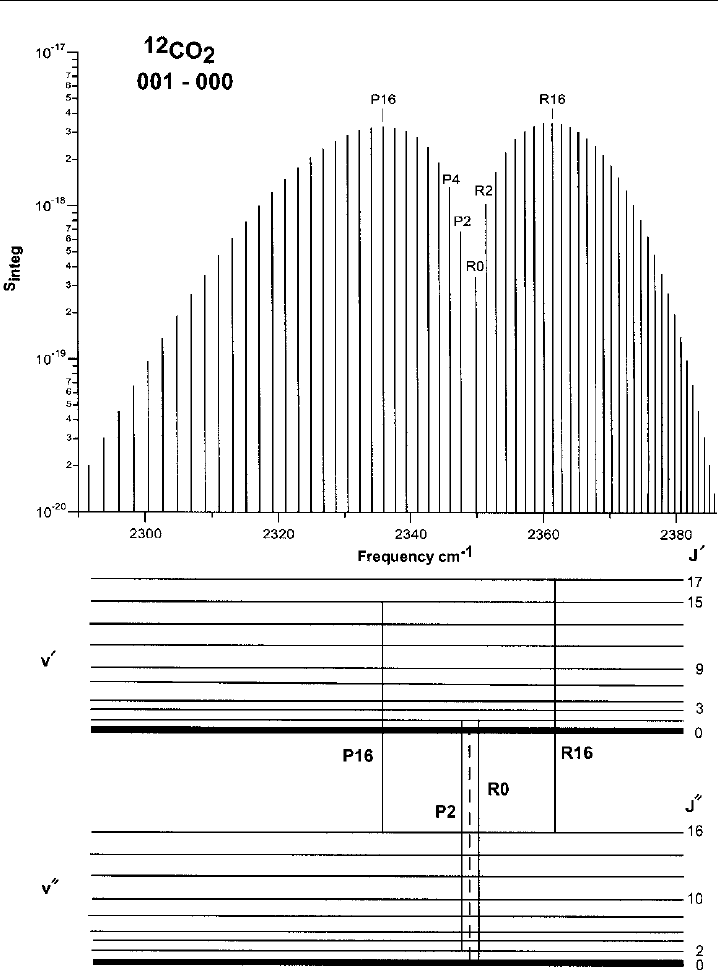
For illustrative purposes, we show in Figure 2.3 the band structure and associated
rotational features for the asymmetric stretching vibration of the linear molecule CO
2
.
As can be seen, the P-branch features form a progression at lower frequencies from the
band origin, while the R-branch features form a progression at higher frequencies. As in
all symmetric triatomic molecules, where the O atoms are equivalent, in CO
2
alternate
rotational lines are absent. We will further discuss the rotational lines of Figure 2.3
in relation to line intensities in Section 2.2.5. In nonlinear polyatomic molecules, one
encounters more complicated rotational structures since one must consider more than
one axis of rotation. Further discussion of this topic will not be considered here.
In polyatomic molecules one resolves the various vibrational motions into a sum of
normal vibrations where all atoms in the molecule oscillate with the same frequency and
simultaneously pass through their equilibrium positions. In linear polyatomic molecules,
where each atom possesses 3 translational and 2 rotational degrees of freedom, there are
3N −5 vibrational modes. In nonlinear polyatomic molecules, there are 3N −6 vibrational
modes due to the 3 translational and 3 rotational degrees of freedom. Therefore IR
absorption spectra in polyatomic molecules consist of a series of different vibrational–
rotational features for each mode of vibration. Each distinct mode of vibration is called
a band. Different vibrational bands for a given molecule often appear in different regions
of the IR, and the larger the molecule the greater the number of vibrational bands.
In some texts, the actual vibrational quantum numbers for the transitions are given.
For example, for nonlinear triatomic molecules like H
2
O (3 normal modes of vibration)
one designates the vibrational transitions by the following notation:
1
2
3
upper state
←
1
2
3
lower state
where here is not to be confused with the frequency in Equation 2.2. By convention,
the highest frequency vibration within each symmetry type (see Chapter 3 of Banwell
and McCash, 1994) is designated by the lowest subscript and this designation progresses
to higher subscripts as the frequency decreases. In the case of H
2
O, symmetric stretching
transitions involve the quantum number
1
, and the fundamental band (one quantum of
excitation) has a band origin at 3657 cm
−1
and is designated by the notation 100 ← 000.
Frequently, one simply uses the shorthand notation
1
to designate such a transition.
Infrared Absorption Spectroscopy 79
Figure 2.3 Vibrational-rotational transitions and energy levels for the asymmetric vibrational mode,
3
,
of the
12
CO
2
molecule at a temperature of 296 K. The top panel displays the integrated line intensities
(S
integ
in units of cm
2
cm
−1
molecule
−1
) and the lower panel displays the energy levels, the spacings for
which are not drawn to scale. The band origin is displayed by the dashed line.

80 Analytical Techniques for Atmospheric Measurement
The bending vibrations of H
2
O (same symmetry as above) involve the quantum number
2
, and the fundamental band has an origin at 1595 cm
−1
and a designation 010 ←000.
The asymmetric stretching vibration (different symmetry) involves the quantum number
3
and the fundamental band has an origin at 3756 cm
−1
and a designation 001 ← 000.
As discussed previously, not all vibrational modes appear in the IR (i.e. are IR active).
Figure 2.4 shows the three IR active bands of H
2
O and the two IR active bands of
CO
2
; the
1
symmetric stretch of CO
2
does not produce a change in dipole moment,
and hence this band is IR inactive. By contrast, all normal vibrations in asymmetrical
polyatomic molecules, like the
1
symmetric stretch of HCN, are IR active. In degenerate
bending vibrations of linear polyatomic molecules (e.g. the
2
bending vibration of CO
2
),
a superscript appears above the bending quantum number, and this signifies the presence
of l-doubling, which splits the vibrational levels.
One can further analyse the integral in the second term of Equation 2.7 to qualitatively
assess the strength of vibrational transitions. For non-zero values of the dipole moment
derivative, the integral on the right hand side of Equation 2.7 is non-zero when the
vibrational quantum number changes by ±1 ±2 ±3The most intense absorption
transitions occur when the vibrational state for one vibrational mode at a time changes
by 1 quantum number, that is by +1. Such transitions, which are called fundamental
transitions or fundamental bands, occur in the mid-IR spectral region. The
1
transition
above for H
2
O is an example of this. Since vibrational motions are anharmonic, combi-
nation and difference bands may also appear in the mid-IR spectral region as long as
there is a change in dipole moment. In this case more than one vibrational mode at a
time is excited. In a combination band, one can observe transitions involving
1
+
2
, for
example, while transitions involving
1
−
2
exemplify a difference band. Combination
ν
1
Symmetric, IR inactive
3N – 5 = 4 fundamental vibrational
modes of CO
2
, 2 IR active
C
OO
ν
3
Asymmetric, IR active, very strong
C
OO
–
C
OO
C
OO
+
–
ν
2
Degenerate bending, IR active, very strong
ν
1
Symmetric, IR active, strong
3N – 6 = 3 fundamental vibrational
modes of H
2
O, 3 IR active
O
H
H
O
H
H
ν
2
Bending, IR active, very strong
O
H
H
ν
3
Asymmetric, IR active, very strong
Figure 2.4 Normal vibrational modes for the linear molecule CO
2
and the non-linear molecule H
2
O.
The arrows show the atomic displacements during the vibration. The − and + on the atoms of CO
2
show
these displacements in and out of the plane of the page.

Infrared Absorption Spectroscopy 81
and difference bands are generally significantly weaker than fundamental bands. For
example, the strongest line in the
3
fundamental of CO
2
shown in Figure 2.3 is the
R(16) rotational line, which has an integrated intensity of 35×10
−18
cm
2
cm
−1
molecule
−1
at 296 K. This same rotational line in the combination band 101 ← 000, where the
symmetric and asymmetric stretch each have one quanta of excitation, has an integrated
intensity weaker by a factor of 60 times. Overtone vibrational transitions may also occur.
In this case the vibrational quantum number changes by +2 +3, and these appear
at shorter wavelengths in the near-IR and in some cases in the visible region. Such
transitions are significantly weaker than fundamental transitions, typically by an order of
magnitude or more for each change in vibrational quantum number above +1. The R(16)
line in the 201 ← 000 overtone-combination band of CO
2
, which occurs at 196 min
the near-IR, has an integrated line intensity weaker by a factor of 139 times than the
101 band. When detecting gases like CO
2
and H
2
O, working with near-IR overtones is
generally not a limitation, since the ambient concentrations are so large and the laser
sources and detectors are significantly better than those for the mid-IR spectral region.
However, detection of most trace gas species still requires the significantly stronger mid-IR
fundamental absorption lines.
Two other types of vibrational bands may also appear in the IR: hot bands and isotopic
bands. Hot bands (where the lowest vibrational state is not the ground state) only become
important at high temperatures such as in flames and in combustion stacks where there is
a significant population of molecules in high vibrational levels. The relationship between
absorption strength and ground vibrational population will be presented shortly in a
later section. Isotopic bands, like that of
13
CO
2
, are very similar in nature to the main
isotope of
12
CO
2
, shown in Figure 2.3, only displaced at lower frequencies. The band
origin occurs at 2284 cm
−1
. However, atmospheric absorption lines from such bands are
significantly weaker than the main isotope due to the lower isotopic abundance (∼ by a
factor of 99 in this case).
2.2.4 Vibrational bands of atmospheric spectral features in
the mid-IR
Figure 2.5 shows a plot of the fundamental absorption bands in a narrow window
of the mid-IR spectral region for four major atmospheric constituents, and Table 2.1
tabulates the band origins and integrated band intensities for these and other species from
Smith et al. (1985) and Pugh and Rao (1976). This is only a select list of atmospheric
absorbers, and the interested reader is referred to the references above as well as the 2000
HITRAN database (Park et al., 1987; Goldman et al., 2002; Rothman et al., 2003) for
more comprehensive lists and spectral atlases. In addition, Maki and Wells (1991) and
Guelachvili and Rao (1986) provide spectral maps and transitions of select absorption
lines used in the wavenumber calibration of IR spectrometers. Figure 2.5 plots these four
atmospheric constituents using the mixing ratios shown, which are typical of values found
in the troposphere. As can be seen, CO
2
absorption features in the 4 m spectral region are
extremely strong, and, under the conditions given, could mask much weaker absorptions
by trace species in this region. Water vapor absorptions near the fundamental band
origins given in Table 2.1 could also present similar problems for trace gas measurements
