Hawkes P.W., Spence J.C.H. (Eds.) Science of Microscopy. V.1 and 2

Подождите немного. Документ загружается.

Chapter 1 Atomic Resolution Transmission Electron Microscopy 45

optimum solution for ψ′

(k) can be deﬁ ned in various ways (Saxton,

1988). In particular, a Wiener ﬁ lter applied to a series of images (Schiske,

1973) in the presence of noise gives an optimal estimate of the recon-

structed wavefunction, expressed in the form of a weighted superposi-

tion of the individual transforms as

′

∑

() ()()kkkrc

(53)

in which the restoring ﬁ lters, r

(k), depend on the w

(k) for the set of

images as

W C w

W W C

i i

( )

( ) *( ) ( )

( ) ( ) ( ) ( )

() (

k k k k

− − −

− − +

))() ()()

Cww

kkk=−

∑∑

(54)

From Eq. (55) above it can be seen that the effect of the restoring

ﬁ lters on a Fourier component transmitted in only a single image is

simply to retain it after division by the corresponding transfer function

and for Fourier components present in multiple images to average the

estimates. For a Fourier component not transferred in any image the

value of the ﬁ lter tends to zero due to the inclusion of the noise-to-

object power ratio, ν(k).

In the ﬁ nal step of the overall reconstruction

process the exit-plane wavefunction itself is obtained simply by inverse

transformation.

For completeness we also provide an alternative formulation of

through focal series restoration by Spence (2002), which gives useful

insight into the behavior of the various terms and clearly illustrates the

general power of coherent detection methods.

The image amplitude under the WPOA for a single image at a

defocus, C

is given as

ψσφ

in p

iFPiW

FP iW

() (){()exp[ ( )]}

() ()exp[ (

xxkk

xk k

=− −⋅

=⋅

)]

{}

(55)

with an image intensity

IC C

CCh

nin

ini n

() ()

()

=+ + +

ψψ

(56)

where h are the higher order, nonlinear terms.

We are now able to extract the wanted second term in Eq. (56) and

discriminate against the conjugate and the higher order terms.

To effect this we ﬁ rst multiply the transform of the intensity by the

conjugate of the transfer function to deconvolve it and then sum over

N images recorded at different defoci.

This gives

This is the major advantage of the Wiener ﬁ lter in preventing noise

ampliﬁ cation where w

(k) is close to zero.

SICiWC

() ( )exp[ ( )]

() () *( ) exp[

kk k

=−

=+ +− −

∑

12δφ φ (()]

()exp[ ( )]

HC iW C

nn n

∑∑

∑

+−

(57)

where φ(k) = 1 − iσF {φ

(x)} is the image we wish to restore.

Equation (57) now clearly shows the power of coherent detection.

The second term sums as N times the wanted image, whereas the

unwanted third and fourth terms sum as N

1/2

times their initial values.

The ﬁ nal term behaves as a two-dimensional random walk. Overall

the effects of the coefﬁ cients of the wave aberration function appear to

have been eliminated and the only remaining resolution limiting effect

is the function P(k).

A further independent formulation of a linear restoration scheme

similar to that described above, known as the parabaloid method, has

also been reported (Op de Beeck et al., 1996; Thust et al., 1996a,b). This

is based on a three-dimensional Fourier transform of a through focal

series of images with the third variable conjugate to the defocus. The

exit-wave sought is localized on a parabolic shell in this three-

dimensional space and can readily be separated from the conjugate

eave and the nonlinear terms. This approach has the attraction of pro-

viding intuitive insight into how the information from a series of

images is gathered to yield the complex exit-wave, although unlike the

Wiener ﬁ lter it is nonoptimal in its suppression of the conjugate wave

and experimental noise (Saxton, 1994).

The approaches for exit-plane wavefunction restoration described

above assume linear imaging. An alternative method has also been

An alternative imaging geometry for use in reconstruction uses a

dataset recorded for several different illumination tilts (of the same

magnitude but with different azimuths) (Kirkland et al., 1995, 1997) in

a super resolution scheme also referred to as aperture synthesis. The

basis of this approach relies on the fact that for an incident beam tilt

We note that the above describes a general approach of integration against

a kernel to provide a stationary phase condition for a wanted signal and as

such ﬁ nds widespread application throughout physics.

A.I. Kirkland et al.

tions to the image intensity. In the original implementation of this latter

developed for a more general case, including the nonlinear contribu-

approach (Kirkland et al., 1985; Kirkland, 1984, 1988) the nonlinear

multiple input maximum a posteriori (MIMAP)]. The more recent

improved maximum likelihood (MAL) description (Coene et al., 1992,

calculated from the restored wave to the measured intensities of images

numerically optimized recursive solution and explicitly includes the

coupling between the exit wave and its complex conjugate.

image reconstruction is accommodated by matching the intensities

1996; Thust et al., 1996a) provides a computationally efficient and

in a focal series through minimization of a least-squares functional [the

Chapter 1 Atomic Resolution Transmission Electron Microscopy 47

of a Bragg angle Θ

the optic axis bisects the angle Θ = 2Θ

between

the incident beam and a ﬁ rst-order Bragg beam. For this geometry the

two beams deﬁ ne the diameter of an achromatic circle (for positive C

)

on which all even-order terms on the wave aberration function cancel.

However, only one sector of the diffraction pattern contributes to each

image and it is therefore necessary to record images at several (mini-

mally four) different tilt azimuths. The method is also restricted to

relatively thin samples due to the effects of parallax (Kirkland et al.,

1997). The restoring ﬁ lters required are of a form similar to those used

for focal series reconstruction but with the transfer functions modiﬁ ed

so as to be appropriate to tilted illumination (Saxton, 1988). The advan-

tage of this geometry is in the improved ﬂ at information transfer, albeit

in only one direction in a single image, with the disadvantage of poorer

low-frequency transfer in the restored wave. In this way spatial fre-

quencies up to twice the conventional Scherzer limit can be recovered

from a dataset composed of four tilted illumination images recorded

with orthogonal tilt directions (Kirkland et al., 1995).

It is also worth noting that although the reconstructed wavefunction

is free of artefacts due to the lens aberrations, there still exists a sig-

niﬁ cant discrepancy between absolute values of the experimental and

simulated exit wavefunctions (Meyer et al., 2000a). The cause of this

discrepancy (frequently known as the Stobbs factor; Boothroyd, 1998,

2000), which is also observed in comparisons between conventional

experimental HRTEM images and simulations, remains an active

research area and recent holographic data (Lehmann and Lichte, 2002)

suggest that phonon scattering may make a substantial contribution.

4.2 Experimental Geometries

The most widely applied procedure for exit-wave reconstruction is, as

already described, to record several (or many) images at different focus

levels for which the positions of weak transfer are different. This pro-

vides almost continuous transfer in the recovered exit-wave extending

to the ultimate limits set by the axial coherence envelopes (Figure 1–17).

In practice the dataset for a focal series reconstruction is relatively

easily obtained and typically some 20 or more images separated by

close focal increments can conveniently be recorded on a CCD detector

utilizing external computer control of the microscope. The subsequent

processing involves image registration across the series (to account for

specimen drift) and the determination of the individual imaging con-

ditions (using one of the methods described earlier).

The basic methodology for recording data for use in tilt series recon-

struction is the same as that for focal series but particular attention

must be paid to the image registration (due to the distorted form of

cross-correlation functions involving tilted illumination images) and

to the initial defocus condition. In general, for this geometry optimal

transfer is achieved in the tilted illumination mode (with positive C

)

when C

= θ

with C

and θ being the defocus and illumination tilt

measured in reduced units of (

()C

) and (λ/C

)

1/4

, respectively

(Hawkes, 1980) (Figure 1–17). With the development of aberration-

corrected instruments, this method is further enhanced by the removal

of these restrictions in the absence of C

. In practice a combined

defocus/tilt geometry provides optimal transfer and has the additional

beneﬁ t of providing the required data for the determination of the

aberration coefﬁ cients (see earlier).

4.3 Exit-Wave Restoration of Complex Oxides

To illustrate the beneﬁ ts of exit-wave restoration over conventional

HRTEM imaging we have chosen two examples of complex oxides.

Figure 1–18a shows a structural model of Nb

projected along

Figure 1–17. A comparison of transfer functions. (a) Conventional phase con-

trast transfer function (PCTF) for a single Scherzer defocus image. (b) Effective

wave transfer function (WTF) for a 21-member focal series with a defocus step

between images of 5 nm. (c) Effective wave transfer function for a 6 member

tilt azimuth series with a tilt of 7.7 mrad. (d) Two-dimensional representation

of the effective wave transfer function in (b). (e) Two-dimensional representa-

tion of the effective wave transfer function in (c). In all cases electron optical

parameters appropriate to a 300-kV FEGTEM were used (300 kV, C

= 0.57 nm,

focal spread = 4 nm, beam divergence = 0.1 mrad). (a) Scaled −1 to 1; (b and c)

scaled 0 to 1; (d and e) scaled 0 to 1 (black to white).

A.I. Kirkland et al.

Chapter 1 Atomic Resolution Transmission Electron Microscopy 49

Figure 1–18. (a) Structural model of the complex oxide Nb

projected along [001]. (b) Conven-

tional axial HRTEM image recorded at the Scherzer defocus of a thin crystal. (c) Reconstructed

modulus of the exit-plane wavefunction of Nb

with the marked area enlarged (inset), which

directly shows the cation positions (black) with improved resolution compared to the axial image. The

line indicates a stacking fault with a shift of a third of a unit cell along [010]. (d) Reconstructed phase

of the exit-plane wavefunction with the marked area enlarged (inset). The cation sites in the phase are

recovered with positive (white) contrast and additional weak between the cation atomic columns

which indicate the positions of the oxygen anions are also resolved. The reconstructed phase and

modulus are shown at the same scale. (See color plate.)

[001] together with an axial image recorded at the Scherzer defocus

(Figure 1–18b) and the restored exit-plane wavefunction (Figures 1-18c

and d) recovered to a resolution of ca. 0.11 nm. It is apparent that

although the basic cation lattice can be determined from the axial

image the restored modulus shows the positions of the cation columns

in projection at substantially higher resolution. Moreover, the modulus

remains directly interpretable to a greater specimen thickness than the

axial image. The restored phase shows a more complex contrast chang-

ing rapidly with specimen thickness. In addition to the strong positive

contrast (white, corresponding to a phase advance) located at the cation

sites and corresponding directly to the positions of strong negative

(black) contrast in the modulus there is additional weak contrast at

positions between the cations at the anion sublattice sites.

Our second example illustrates an experimental tilt azimuth series

restoration of an inorganic perovskite with 0.1 nm information transfer.

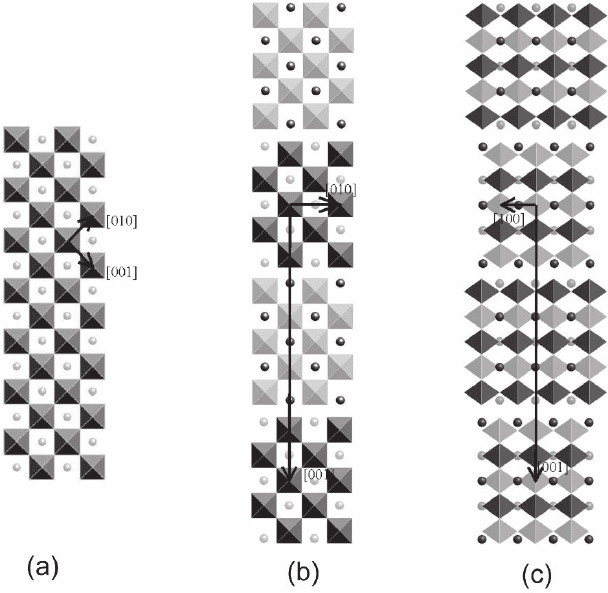
The basic perovskite structure is cubic with general formula ABO

and can be considered as an array of corner-sharing BO

octahedra

where B is typically a small transition metal cation (Figure 1–19). The

cuboctahedral interstices generated by this basic lattice are occupied

by larger A cations, typically alkali earth or rare earth metals. Few

Figure 1–19. Simpliﬁ ed structural models of A

3n+2

compounds represented by corner-sharing BO

octahedra and isolated A cations. Octahedra and cations drawn with light gray shading are half a

lattice plane below those with darker shading. (a) The basic perovskite ABO

. (b and c) The n = 5

structure A

with layers ﬁ ve octahedra wide, projected in the [100] and [010] directions.

A.I. Kirkland et al.

Chapter 1 Atomic Resolution Transmission Electron Microscopy 51

perovskites are cubic and most distort to a lower symmetry to stabilize

the structure.

The layered structure described here (of general formula A

3n+2

)

is composed of slabs of perovskite sliced along the [110] plane with

the two excess oxygen anions accommodated at the interface region

between two slabs (Figure 1–19). These structures show similar distor-

tions to bulk perovskites but with additional degrees of freedom at the

interface.

The restored exit-plane wavefunction for Nd

in the [010] pro-

jection is shown in Figure 1–20. The restoration again shows improved

resolution in both modulus and phase compared to the conventional

axial image and an enhanced sensitivity to the weakly scattering

oxygen sublattice in the restored phase. Comparison with the struc-

tural model shown in Figure 1–19 shows that the Ti are bridged by O

anions and correspondingly in the restored phase, the Nd rows show

distinct cations whereas the Ti rows also show weak contrast between

the cation sites (Figure 1–20) corresponding to the anion positions. The

reconstruction also reveals local distortions present in this material by

which the Nd cations at the outside of the perovskite slabs are dis-

placed by small amounts in alternate directions (Figure 1–20).

5 Image Simulation

A key step in the process of obtaining quantitative structural informa-

tion from HRTEM images is the calculation of image simulations based

on deﬁ ned structural models and imaging conditions for comparison

with experimental images. As already discussed, simple models for

Figure 1–20. (a) Enlarged region taken from the reconstructed modulus calculated from a tilt azimuth

dataset of an Nd

SrTi

crystal edge in the [010] projection showing a small difference in positions

of the Nd(4) and Nd(5) cations at the interface between adjacent perovskite slabs. (b) Reconstructed

phase of the same region as (a) showing details of the oxygen anion sublattice between the Ti sites.

The experimental data were recorded using the tilt series geometry described in the text with a JEOL

JEM-3000F FEGTEM, 300 kV, C

= 0.57 mm with an injected tilt of 1.9 mrad. (See color plate.)

electron scattering and imaging at high resolution suffer from limita-

tions and in general, computationally tractable N-beam dynamic cal-

culations are essential to this process.

For this purpose, the multislice method is most commonly used to

compute the electron wave at the exit-plane of a specimen with known

atomic structure. This approach was ﬁ rst suggested by Cowley and

Moodie (1957) and has found extensive use in HRTEM simulation

(Goodman and Moodie, 1974). In particular, the availability of efﬁ cient

Fast Fourier Transform (FFT) algorithms and the general increase in

readily available computing power have made earlier constraints on its

accuracy due to limitations in the number of slices or the number of

diffracted beams immaterial.

An alternative to the multislice method is the Bloch wave approach,

ﬁ rst introduced by Bethe (1928) and described in detail, for instance,

in Buseck et al. (1989). By analogy with the Bloch theorem in solid-state

physics, the solution of the Schrödinger equation in a periodic crystal

potential is written as a product of a plane wave and a function that

has the same periodicity as the crystal. The latter function is then

expanded into its Fourier components from which the Schrödinger

equation reduces to a matrix equation in these Fourier coefﬁ cients. For

simple crystals, relatively accurate solutions can be obtained using only

a few of these Bloch waves, with the minimal case requiring only two

(the two beam approximation). This approach has the advantage of

providing valuable insight into the working of dynamic electron dif-

fraction and explains phenomena such as thickness fringes. However,

for complex crystals with large unit cells, the method becomes imprac-

tical, as a large number of beams has to be used in the calculation and

the computation time for the matrix solution scales with N

, where N

is the number of beams included. For this reason it has only rarely been

applied to calculations of HRTEM images.

Finally we note that for the majority of cases matching of experimental

and simulated images is carried out purely visually with limited attempts

to deﬁ ne quantitative ﬁ gures of merit (FOM) describing the differences

between experimental and simulated images (or restored exit wavefunc-

tions). In part this is due to the large number of parameters involved in

HRTEM simulations (including atomic coordinates and those describ-

ing imaging conditions) giving rise to a large multiparameter optimiza-

tion problem with many local minima. However, a number of possible

FOMs have been reported (Mobus et al., 1998; Tang et al., 1993, 1994;

Saxton, 1997) based on comparisons in both image and Fourier space.

5.1 The Multislice Formalism

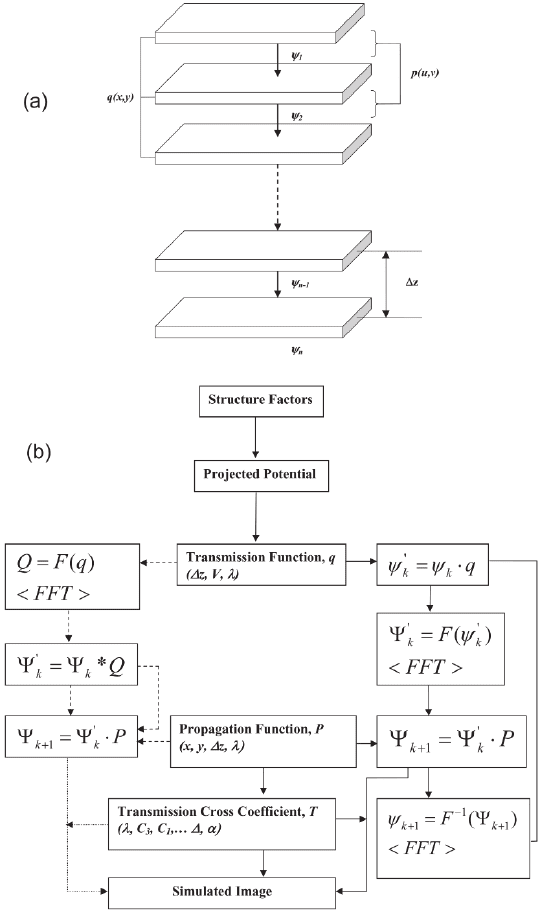
The formal basis of the multislice method (for an extensive treatment

see Kirkland, 1998) is the division of the specimen into a number of

thin slices perpendicular to the direction of the incident beam. The

effects of the specimen potential (transmission, in real space) and of

Fresnel diffraction (propagation, in Fourier space) are than treated

separately for each slice (Figure 1–21). It is a requirement that the indi-

vidual slices used in the simulation must be thin enough to be weak

A.I. Kirkland et al.

Chapter 1 Atomic Resolution Transmission Electron Microscopy 53

Figure 1–21. (a) Schematic diagram showing the real space transmission and

fourier space propagation steps. (b) Flow chart illustrating the steps involved

in a multislice simulation.

phase objects and that they obey periodic boundary conditions per-

pendicular to the incident beam direction.

The equations central to the multislice algorithm can be formally

derived starting from the Schrödinger equation for the wavefunction

, of an electron in the electrostatic potential V (x, y, z) of the

specimen:

−∇−

(

)













(

)

(

)



eV x y z xyz E xyz,, ,, ,,

ψψ

(58)

where m is the relativistically corrected electron mass. For high-energy

electrons, the motion is predominantly in the z direction. Hence, it

is convenient to separate the full wavefunction, ψ

, into a product of

the solution of the free Schrödinger equation (with V ≡ 0), which is a

plane wave propagating in the z direction, and a wavefunction ψ

that represents the effects due to the specimen and varies much more

slowly with z:

(x, y, z) = e

2πkz

⋅ ψ(x, y, z) (59)

where k = 1/λ is the inverse wavelength of the free electron. Substitut-

ing this into Eq. (58) and using E = h

/2m yields

−∇+

∂

(

)













(

)



meV x y z

xyz

πψ

(60)

In an elastic scattering process away from the z direction, k

and k

are proportional to the scattering angle, while the change, ∆k

, is pro-

portional to its square. For small scattering angles therefore the term

|∂

ψ/∂z

|<<|∇

ψ| and can be neglected in the paraxial approximation.

What remains is a ﬁ rst-order differential equation in z

∂

(

)

∂

[]

(

)

xyz

AB xyz

,, (61)

with the operators

=∇

π4

(62)

B = iσV (x, y, z) (63)

and the interaction parameter σ deﬁ ned here as

πλ

(64)

This differential equation has the formal solution

ψψxyz z Az Bz dz xyz

,, ,,+

(

)

′

()

′

()

[]

′













(

)

∫

∆

exp (65)

When ∆z is small, this reduces to

It should be noted that k is deﬁ ned here as 1/λ rather than 2π/λ and

therefore h rather than

h is used in the expression for E.

A.I. Kirkland et al.