Hawkes P.W., Spence J.C.H. (Eds.) Science of Microscopy. V.1 and 2
Подождите немного. Документ загружается.

Chapter 1 Atomic Resolution Transmission Electron Microscopy 15
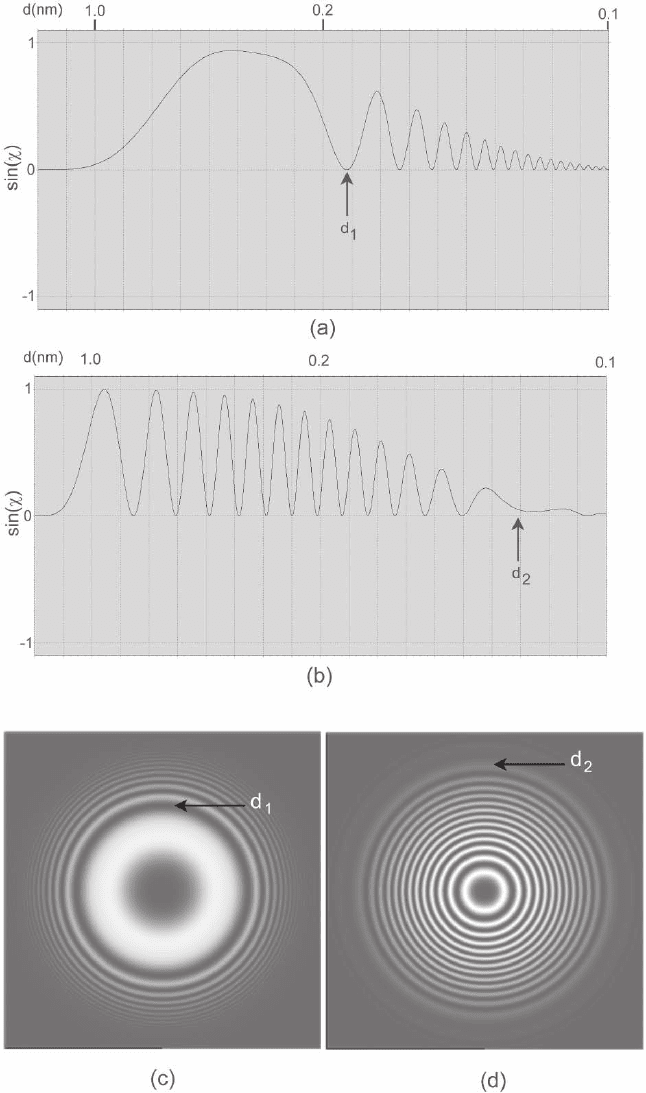
Figure 1–6. Phase contrast transfer functions (PCTFs) plotted in one dimension (a and b) and two
dimensions (c and d) calculated for a modern 300-kV FEGTEM illustrating the interpretable resolution
(d
1
) and information limits (d
2
). (a and c) calculated at the Scherzer defocus (−34.4 nm) (b and d) cal-
culated at the higher Lichte underfocus (−174.4 nm). In all cases CTFs are calculated for 300 kV, C
3
=
0.6 mm, ∆E = 0.8 eV, beam divergence = 0.1 mrad and the interpretable and information limits are
indicated.

16
As will be discussed in detail in a subsequent section the effects of
temporal and spatial coherence (see also Hawkes and Kasper, 1996) can
be treated through respective envelope functions of form
EqCC
f
s
) }
() exp{ ( )}kkk=− +πλλ
2 2 2 2
2
0
2
13
332
(20)
in which the expression for the spatial envelope includes only defocus
and spherical aberration, with q
0
, the standard deviation of a Gaussian
modeling the convergent cone of illumination at the specimen surface,
and where
∆= + +
C
V
V
I
I
E
V
c
σσσ
2
0
0
2
2
0
0
2
2
0
0
2
12
4() () ()
(21)
In Eq. (21) C
c
is the chromatic aberration, E
0
is the spread in electron
energies arising from the source, V
0
is the accelerating voltage, and I
0
is the objective lens current, which affects the objective lens magnetic
fi eld (O’Keefe, 1992).
8,9
The form of these distributions is far less important than their width
and in general, as above, Gaussian distribution functions are used, as
this makes any further derivation analytically tractable.
10,11
The form of these two envelope functions leads to defi nitions of
information limits in which the information transfer drops to a level
of exp(−2) or 13.5% given by (O’Keefe and Pitt, 1980).
d
d
dS S
S
q
C
Cq
2
3
=
=+
=± +
+−
±
πλ
πλπ
2
33
427
33
4
13
13
0
1
3
3
2
0
2
..
12
3
2
C λ
(22)
However, it should be noted that the limit defi ned by d
3
increases with
defocus and does not therefore defi ne an absolute information limit
8
The last term is written here in terms of the objective lens current I
0
following convention. However, this is not strictly correct, particularly if the
lens is operated close to saturation where the magnetic fi eld is not proportional
to the current.
9
It may seem surprising that the objective lens current infl uences the
variation of focus only in the presence of chromatic aberration. However, this
is due to the general scaling rule that electron trajectories are identical when
energy and magnetic fi eld are changed according to E′ = k
2
E and B′ = kB.
Hence, in a microscope corrected for chromatic aberration, the focus cannot
be changed by changing the currents in all lens elements by the same factor.
10
For the defocus spread, the terms due to voltage and lens current instabilities
are well described by Gaussian function, whereas the intrinsic source energy
spread would be more accurately described by a Maxwellian distribution for
thermionic emitters or the Fowler–Nordheim equation (Fowler and Nordheim,
1928) for fi eld emitters.
11
The above defi nition of δ assumes that the fl uctuations are independent of
each other.
A.I. Kirkland et al.
k− π λ∆ (E (k) = exp 0.5{
Chapter 1 Atomic Resolution Transmission Electron Microscopy 17
per se. In particular, for the case of fi eld emission sources where the
source size is small, the spatial coherence is not limiting and thus the
information limit due to temporal coherence determines the informa-
tion limit for all defoci.
2.3 The Wave Aberration Function
The key optical component affecting HRTEM image formation is the
objective lens and in this section we review its infl uence in terms of
the wave aberration function (see also Hawkes and Kasper, 1996).
For an ideal lens, a point object at a position (x, y) in the object plane
leads to a spherical wavefront in the diffraction plane, contracting to a
conjugate point in the image plane.
12
However, all electromagnetic
lenses suffer from aberrations causing deviations from this ideal spher-
ical wavefront thus reducing the sharpness of an image point much
more severely than the diffraction limit.
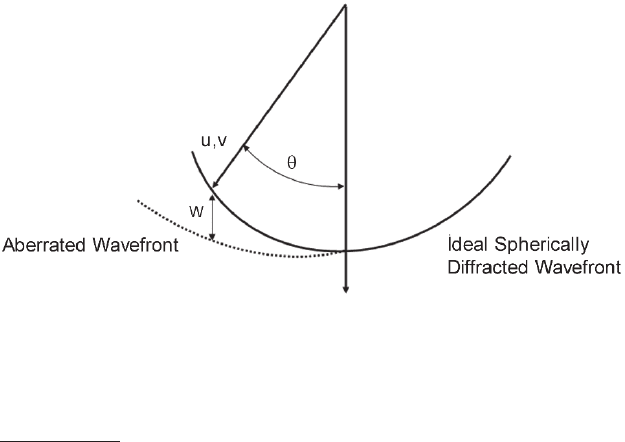
For HRTEM, a wave aberration function W(u, v) is therefore defi ned
that describes the distance between the ideal and actual wavefronts in
the diffraction plane as a function of the position of the point object in
the diffraction plane, (u, v) (Saxton, 1995) (Figure 1–7).
13
The wave aberration function, W(ω), written in terms of a complex
position variable ω = u + iv can be Taylor expanded to 3rd order in
terms of the axial aberrations as
Figure 1–7. Schematic diagram showing the origin of the wave aberration
function, W(u,v), which describes the complex deviation from an ideal spheri-
cally diffracted wave.
12
For a pure phase object this condition would, however, lead to lead to zero
contrast at the Gaussian focus.
13
More rigorously W is a function of both position of the point object in the
diffraction and image planes, i.e., W(x, y, u, v). However, HRTEM experiments
are carried out at high magnifcation and hence the feld of view is small
and the dependence of W on (x, y) can be neglected in the isoplanatic
approximation.

18
(23)
Converting to polar notation, with ω = ke
iφ
, A
n
= |A
n
|e
iα
n
and B
n
=
|B
n
|e
iβ
n
, Eq. (23) can be more conveniently rewritten as
(24)
which makes the azimuthal and radial dependence of the various aber-
ration terms more apparent.
Table 1–2 lists the aberration coeffi cients important in HRTEM ignor-
ing those with a chromatic dependence.
14
All of the aberration coeffi cients listed in Table 1–2 except C
1
and C
3
are due to lens imperfections (either mechanical or electrical) and
would not appear in a perfect round lens (Scherzer, 1949). However,
they can be corrected using combinations of multipole fi elds of appro-
priate symmetry and in recent years this approach has enabled the
Table 1–2. Isoplanatic aberration coeffi cients important for
HRTEM.
Aberration Order in w Azimuthal symmetry Name and description
A
0
1 1 Image shift
A
1
2 2 Two-fold astigmatism
A
2
3 3 Three-fold astigmatism
A
3
4 4 Four-fold astigmatism
B
2
3 1 Axial coma
S
3
4 2 Axial star
C
1
2 • Defocus
C
3
4 • Spherical aberration
14
The seemingly counterintuitive notation (e.g., C
1
in Table 1–2 for a second-
order term in the wave aberration fucntion stems from the ray-optical theory
of Seidel aberrations (Hawkes and Kasper, 1989), which are described in
terms of displacements of ray-path intersections with the image plane as a
function of (u,v). These displacements are proportional to the gradient of the
wave aberration function and hence an nth-order Seidel aberration corresponds
to a term of order n + 1 in the wave aberration function.
A.I. Kirkland et al.
W (ω) = <{
2π
λ
{A
0
λω
∗
+
1
2
A
1
λ
2
ω
∗2
+
1
2
C
1
λ
2
ω
∗
ω
+
1
3
A
2
λ
3
ω
∗3
+
1
3
B
2
λ
3
ω
∗2
ω
+
1
4
A
3
λ
4
ω
∗4
+
1
4
S
3
λ
4
ω
∗3
ω +
1
4
C
3
λ
4
ω
∗2
ω
2
+ . . .}}
W (k, φ) =
2π
λ
{|A
0
|λk cos(φ − α
0
)
+
1
2
|A
1
|λ
2
k
2
cos 2(φ − α
1
) +
1
2
C
1
λ
2
k
2
+
1
3
|A
2
|λ
3
k
3
cos 3(φ − α
2
) +
1
3
|B
2
|λ
3
k
3
cos(φ − β
2
)
+
1
4
|A
3
| λ
4
k
4
cos 4(φ − α
3
) +
1
4
|S
3
|λ
4
k
4
cos 2(φ − σ
3
)
+ . . .}
+
1
4
C
3
λ
4
k
4

Chapter 1 Atomic Resolution Transmission Electron Microscopy 19
Table 1–3. Accuracy of aberration coeffi cients.
a
Resolution Accuracy
K
max
(/nm
-1
) d
min
(nm) A
1
, C
1
(nm) A
2
, B
2
(nm) A
3
, S
3
, C
3
(mm) Tilt (mrad)
11 0.09 0.5 35 2.1 21
10 0.1 0.6 47 3.1 27
9 0.11 0.8 64 4.8 38
8 0.125 1.0 92 7.6 54
7 0.14 1.3 137 13 80
a
Accuracy to which the aberration coeffi cients need to be determined such that each of them causes a maximum
RMS error in the wave aberration function of less that λ/16, i.e., a phase change of less than π/8 for a given target
resolution. The values are calculated for an accelerating voltage of 300 kV (λ ≈ 2 pm). The necessary accuracy for
the beam tilt τ is calculated from that for B
2
using ∆τ = −∆B
2
/(3C
3
) with C
3
= 0.57 mm.
correction of C
3
using long hexapole fi elds (see later) (Rose, 1981, 1990;
Haider et al., 1998c; Urban et al., 1999).
For HRTEM imaging the effects of the coeffi cients of the wave aber-
ration function are to introduce phase shifts in the image given by
multiplying each term in W by 2 π/λ. These phase shifts can also be
used to estimate the maximum tolerable value in any coeffi cient for a
particular target resolution (Table 1–3).
Few of the aberration coeffi cients defi ned above are directly observ-
able under axial illumination and their determination therefore relies
on measurements taken as a function of known injected beam tilts.
If the illumination is tilted by an angle τ the new aberration coeffi -
cients up to C
3
(marked with a prime) are given by
′
=+ + + + + +
′
=+
AAA A C B B C
AA A
001 2
2
12
2
23
2
11 2
2
1
3
2
3
2
ττ τ τ ττ ττ
ττ
**
*
**
* +++
′
=+ +
′
=
′
=+
′
=
2
3
4
3
2
3
23
2
11 2 3
22
22 3
33
BC
CC B C
AA
BB C
CC
ττ
τττ
τ
R(*) *
(25)
From Eq. (25) it is immediately apparent that the shift A′
0
− A
0
between two images taken at beam tilts differing by τ depends on all
the other aberration coeffi cients. Hence, measuring the image shifts
induced by a suitable set of beam tilts provides a method for measuring
all coeffi cients.
Alternatively, the tilt-induced changes, C′
1
− C
1
and A′
1
− A
1
in defocus
or two-fold astigmatism measured from diffractograms (Figure 1–8),
depend on A
1
, C
1
, A
2
, B
2
, and C
3
, thus providing an alternative measure
of these coeffi cients. If the spherical aberration is independently deter-
mined then measurement of the orientations only of diffractograms also
provides another simple measure of A
1
, A
2
, and B
2
(Saxton, 2000).
Measurements of diffractograms (Krivanek, 1976; Krivanek and
Leber, 1994; Zemlin et al., 1978; Zemlin, 1979; Typke and Dierksen, 1995;
Pan, 1998; Saxton, 1995) or image shifts (Typke and Dierksen, 1995;
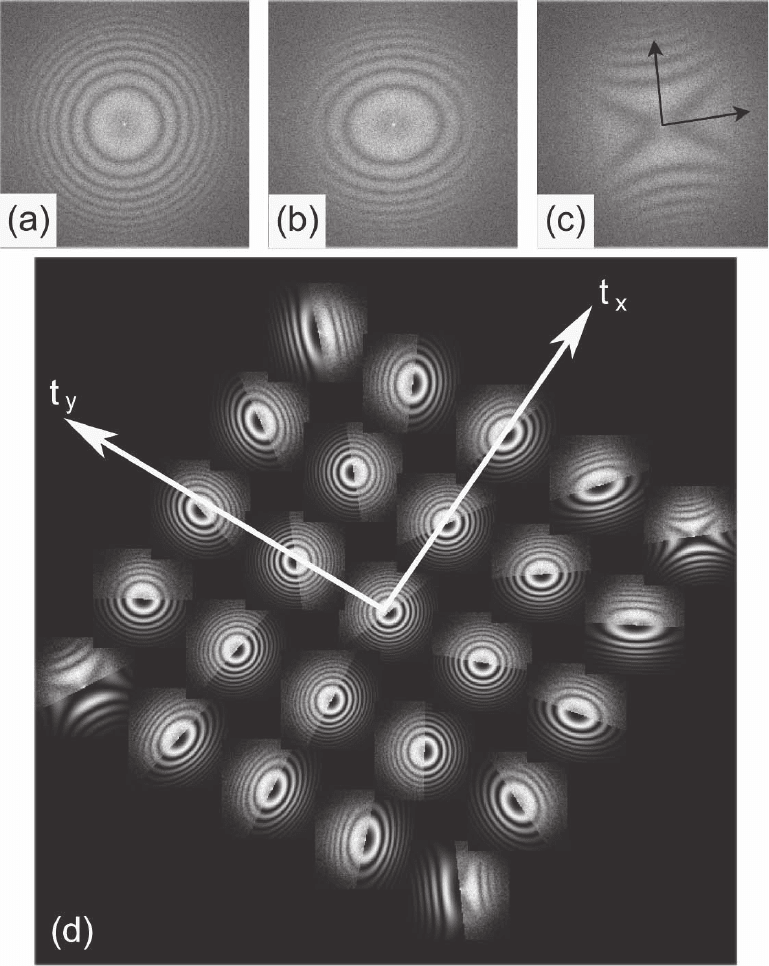
20
Figure 1–8. Individual axial diffractograms calculated from HRTEM images of a thin amorphous
germanium foil showing the effects odefocus (C
1
) and two-fold astigmatism (A
1
). (a) Axial image
recorded at large underfocus with the two-fold astimatism corrected. (b) Axial image in the presence
of a small amount of two-fold astigmatism giving rise to an elliptical diffractogram. (c) As for (b) but
with a larger two-fold astigmatism giving rise to a “Maltese Cross”-shaped diffractogram showing
overfocus and underfocus along the axes indicated. (d) Representative tableau of diffractograms
recorded for a set of differently titled illumination conditions illustrating the variation in A
1
and C
1
with illumination tilt. Each experimental diffractogram is shown merged with a simulated diffracto-
gram calculated from the fi tted values of A
1
and C
1
. The illumination tilt axes are indicated.
A.I. Kirkland et al.

Chapter 1 Atomic Resolution Transmission Electron Microscopy 21
Koster et al., 1987, 1989; Koster, 1989; Koster and de Ruijter, 1992; Saxton,
1995), however, have their own particular experimental advantages
and disadvantages.
A practical diffi culty with the application of tilt-induced displace-
ments arises from the measurement of the image shifts using the peak
position in the cross-correlation function defi ned as
XCF =
−
FT c c
1
12
[
*
]
(26)
The tilt-induced change in A
0
introduces a linear phase variation in
the cross spectrum c*
1
c
2
, which leads to a displacement of the XCF peak
to a position given by the shift vector between the images. As already
shown, the other imaging parameters also change as the beam is tilted
and this causes the phase variation to become nonlinear at higher
spatial frequencies and leads to distorted cross-correlation peaks.
However, when the imaging conditions in both images are approxi-
mately known, these nonlinear phase shifts can be compensated and
a sharp XCF peak can be recovered (Saxton, 1994; Kirkland et al., 1995).
Shift measurements also fail for clean perfectly periodic specimens in
which image positions differing by any integer multiple of a lattice
vector cannot be distinguished. A more severe problem associated
with the tilt-induced shift method is that any displacement due to
specimen drift is indistinguishable from the tilt-induced displacement
required and hence this approach is most frequently used at low reso-
lution or for initial coarse alignment at high resolution.
Conversely, diffractogram measurements require the presence of an
area of thin disordered material and are thus less generally applicable.
However, they are insensitive to specimen drift and their measurement
is relatively straightforward even under tilted illumination conditions.
Hence defocus and astigmatism measurements are best suited to fi ne
adjustment at high resolution (Pan, 1998).
Historically the use of diffractograms for the determination of aber-
rations was fi rst suggested by Thon (1966) for the measurement of
defocus from ring positions in an optically generated diffractogram.
This method was later extended through the use of diffractogram tab-
leaus acquired with different beam tilt azimuths (Figure 1–8) to the
measurement of the spherical aberration C
3
, axial coma B
2
, and three-
fold astigmatism A
2
by Krivanek (1976) and Zemlin et al. (1978).
However, the diffractogram tableau method was computationally too
demanding for routine use at this time and was used only to demonstrate
that the alignment achieved from current reversal or voltage centering
was inadequate as an alignment for HRTEM (Saxton et al., 1983).
15
15
The current reversal center alignment involves reversing the current of the
objective lens and is no longer practical with the strong lenses used in modern
instruments. It should not be confused with the current center alignment,
where the objective lens current is oscillated by a small amount. Similarly, in
the voltage center alignment, the high tension is oscillated. Generally, the axes
found by the three methods are distinct and the voltage center provides a
workable approximation to the coma-free axis, but for HRTEM coma-free
alignment is preferred.

22
Fitting C
1
and A
1
to match simulated diffractogram patterns with
experimental ones can be done manually to relatively high accuracy
(Figure 1–8d; Chand, 1997). This, however, is a lengthy and tedious
process and automation of this task is highly desirable. This problem
has been addressed by Baba et al. (1987) and Fan and Krivanek (1990)
in an algorithm where the diffractogram is divided into 32 sectors and
the defocus along the directions in each sector is determined by cross-
correlating the rotational sector average with an array of theoretical
diffractograms. The sinusoidal focus variation as a function of the
azimuth angle obtained is subsequently fi tted to the measured focus
values to determine C
1
and A
1
and automatic alignment can be achieved
using a tableau with as few as four tilt azimuths.
More generally, the major challenges for implementing a robust auto-
mated diffractogram fi tting procedure are as follows:
1. The most abundant amorphous material in the microscope, carbon,
is a weak scatterer. Hence, particularly at high spatial frequencies,
the signal is weak compared to the noise background affecting
overall diffractogram quality.
2. The strength of the observed signal depends on the object as well
as on the phase contrast transfer function.
3. Diffractograms taken close to Scherzer or Gaussian defocus show
few rings and are diffi cult to fi t.
4. In the presence of large two-fold astigmatism and at close to Gauss-
ian defocus the diffractograms are cross- rather than ring-shaped,
which leads to diffi culties for algorithms based on the evaluation of
rotationally averaged sectors of the diffractogram.
5. It is diffi cult to distinguish between overfocus and underfocus.
6. Most automated algorithms fail when a signifi cant amount of crys-
talline material is present, leading to strong refl ections at positions
unrelated to the ring pattern.
More recently the advent of C
3
-corrected microscopes (see later) has
made automated aberration measurement more important because the
nonround lens elements introduce a multitude of high-order aberra-
tions (up to six-fold astigmatism) that require correction in an elaborate
alignment procedure. Uhlemann and Haider (1998) have implemented
an algorithm that can evaluate the apparent defocus and astigmatism
from a diffractogram in less than 400 ms based on a comparison of the
experimental diffractogram with an extensive library of precalculated
diffractograms and is robust to disturbances from the presence of
crystalline material.
However, given the limitations of both of these traditional methods
an alternative method has also been proposed, which is both applicable
to a wide range of specimens and suffi ciently accurate for use in atomic
resolution imaging (Meyer, 2002; Meyer et al., 2002, 2004).
In this approach a phase correlation function (PCF) (Figure 1–9) (Kuglin
and Hines, 1975) is initially calculated (defi ned as the conventional XCF
with the modulus set to unity):
PCF FT F
cc
cc
() ()
()* ()
()* ()
xk
kk
kk
=
−1
12
12
(27)
A.I. Kirkland et al.

Chapter 1 Atomic Resolution Transmission Electron Microscopy 23
where c
i
(k) are the image Fourier transforms and F(k) is a rotationally
symmetric weighting factor used to suppress high-frequency noise.
The modulus normalization is essential as it suppresses the crystal
refl ections that make the conventional XCF periodic, thus allowing
aberration measurement in the absence of amorphous material.
The PCF calculated between two images recorded at different defocus
levels consists of a centrosymmetric ring pattern, the exact form of
which depends on the relative defocus between them (assuming that
the other aberration coeffi cients remain constant between the two
images) (Figure 1–9). It is possible to compensate for the phase shifts
giving rise to this ring pattern by the application of a phase factor
dependent on the defocus difference, thus defi ning a phase compen-
sated PCF
PCF FT F
Wcc
Wcc
w
D
D
() ()
cos[ ( )]
*
()()
|cos[ ( )]
*
()(
xk
kkk
kkk
=
−1
12
12
))|+
h
(28)
Figure 1–9. Comparison
of a (a) cross- and (b) phase
correlation functions (XFC
and PCF) between two
images of a crystalline
material with a defocus
difference of 69 nm. Due to
the periodicity of the crys-
talline specimen, the XCF
peak repeats periodically
but the PCF dose not show
this repetitive pattern and
consists of a single peak
broadened into a concen-
tric ring pattern due to the
defocus difference.

24
in which the very small positive number, h, prevents a zero denomina-
tor and where W
D
(k) = π∆C
1
λ|k|
2
describes the propagation from the
fi rst to the second image in the presence of only a defocus difference
∆C
1
. When the value of ∆C
1
matches the actual focus difference the
phase compensated PCF collapses to a sharp localized correlation
peak. Hence the relative defocus difference between two images can
be determined by simply maximizing peak height in the phase com-
pensated PCF as a function of the compensated defocus difference
(Figure 1–10), which with subsequent refi nement can yield relative
defoci to an accuracy better than 1 nm (Meyer et al., 2002).
In the second step an initial restored image wavefunction (see later
for details of the restoration process), ψ
i
(k), in the plane of a reference
image is restored and the absolute values of A
1
and C
1
are determined
using a phase contrast index function (PCI) f
PCI
given by
fCA
WCA
PCI si si
,,
,,
()cos[arg(())] arg[ ( )]
()
kkk
k
11
11
2
=− + −
+
ψψ
(29)
where
(30)
Figure 1–10. Peak height of the PCF (solid line) and XCF (dashed line) (shown
against the left hand side and right hand side scales) between two images as
a function of compensated focus difference showing a sharp maximum at the
correct compensating focus difference in the PCF.
A.I. Kirkland et al.
W (k, C
1
, A
1
) =
1
2
|A
1
|λk
2
cos 2(φ − α
1
) +
1
2
C
1
λk
2
+
1
2
C
3
λ
3
k
4
.
