Haug H., Koch S. Quantum theory of the optical and electronic properties of semiconductors

Подождите немного. Документ загружается.

January 26, 2004 16:26 WSPC/Book Trim Size for 9in x 6in b ook2

Semiconductor Bloch Equations 219

The ﬁrst equation of Eq. (12.19) is nothing but the polarization equation

(10.21) supplemented by the scattering term. The factor

1 − n

e,k

− n

h,k

= n

v,k

− n

c,k

is again the population inversion of the state k. Its eﬀects on the optical

absorption spectra are often denoted as Pauli blocking, state ﬁlling,ormore

generally as phase space ﬁlling.

If one ignores all the Coulomb potential terms, V (q) → 0, Eqs. (12.19)

reduce to the free-carrier optical Bloch equations of Chap. 5. As shown

in Chap. 10, the homogeneous part of Eq. (12.19) becomes the general-

ized Wannier equation for electron–hole pairs with the eﬀective Coulomb

interaction being renormalized by the phase-space ﬁlling factor. The term

−2Im

R,k

∗

in the last two equations of (12.19) describes the generation of electrons and

holes pairs by the absorption of light. As long as the scattering terms are

ignored, the rate of change of the hole population (last equation of (12.19))

is identical to the rate of change of the electron population, second equation

of (12.19).

12.2 Multi-Subband Microstructures

Before we proceed with the discussion of the semiconductor Bloch equa-

tions, we will give their formulation for microstructures with several sub-

bands. For free carriers, the density matrix equations have already been

derived in Chap. 5, Eq. (5.36). In terms of the creation and annihilation

operators, we write the reduced density matrix as

i,µ;j,ν

(k,t)=a

†

j,ν,k

(t)a

i,µ,k

(t) . (12.20)

Note the inversion of the indices between left and right hand side of this

deﬁnition. For quantum dots with conﬁnement in all directions, the wave

vector has to be dropped, and the index ν represents the whole set of

quantum numbers for the discrete energy levels.

For the optical transitions between subband µ in the valence band j =

v and subband ν in the conduction band i = c induced by a coherent

light ﬁeld, the optical polarization components are given by the oﬀ-diagonal

January 26, 2004 16:26 WSPC/Book Trim Size for 9in x 6in b ook2

220 Quantum Theory of the Optical and Electronic Properties of Semiconductors

matrix elements

ν;µ

(k)=ρ

c,µ;v,ν

(k)=a

†

v,ν,k

c,µ,k

 . (12.21)

The other relevant matrix elements are the electron occupation probability

for state k in subband ν

e,ν,k

= ρ

c,ν;c,ν

(k)=a

†

c,ν,k

 (12.22)

and the hole occupation probability in subband µ which is given by

h,µ,k

=1− ρ

v,µ;v,µ

(k)=1−a

†

v,µ,k

 . (12.23)

The equation of motion for the density matrix follows from the Heisenberg

equation



[H, A] in the form

†

j,ν,k

i,µ,k

†

j,ν,k

i,µ,k

+ a

†

j,ν,k

i,µ,k

. (12.24)

Since we only want to explicitly compute the Hartree–Fock parts of the

multiband semiconductor Bloch equations, we do not have to use the full

interaction Hamiltonian. It is suﬃcient to work with the Hartree–Fock

Hamiltonian which includes the interaction with the light ﬁeld







,µ



†



,µ



,µ



−E(t)





,µ



,ν



(k)a

†



,µ



,ν



−





,µ



,ν



,ν





,µ



(q)





,ν





,µ



(k−q)−δ





,µ





†



,ν



,µ



(12.25)

This Hamiltonian is obtained by making the Hartree–Fock approximation

in the full many-body multi-subband Hamiltonian. Here, the Coulomb

interaction potential is



,µ



,ν



,ν





,µ



(q)=

2πe





dzdz



∗



,µ



(z)ζ

∗



,ν





)

−q|z−z



,ν





)ζ



,µ



(z) , (12.26)

compare problem 12.2. In deriving Eq. (12.26), we again excluded the

interband Coulomb scattering processes but allowed for intersubband scat-

tering.

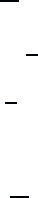
January 26, 2004 16:26 WSPC/Book Trim Size for 9in x 6in b ook2

Semiconductor Bloch Equations 221

In the Hartree–Fock Hamiltonian (12.25), we have subtracted the ex-

change energy with the full valence band, because this Hartree–Fock ex-

change energy is already included in the band structure calculations. Thus

for the terms with j



= i



= v and ν



= µ



the contributions of the va-

lence band subbands to the energy renormalizations are determined by the

hole distribution functions, 1 −ρ

v,µ



;v,µ



(−k)=n

h,µ



(k), in analogy to the

situation in bulk semiconductors.

With the HF Hamiltonian (12.25) one ﬁnds the multi-subband Bloch

equations



+ i



i,µ,k

− 

j,ν,k



i,µ;j,ν

(k)

= −



E(t)





i,µ;i



,µ



(k)d



,µ



;j,ν

(k) − d

i,µ;j



,ν



(k)ρ



,ν



;j,ν

(k)



−





(

i,µ;j



,ν



(k)





,ν



;j,µ



(k−q)−δ



j,v



,µ





j,µ



,ν



,ν



,j,ν

(q)

−V



,µ



,i,µ;i,ν





,µ



(q)



i,ν





,µ



(k − q) − δ

i,v





,µ







,µ



;j,ν

(k)

)

i,µ;j,ν

(k)



scatt

. (12.27)

Here, we have added the scattering terms which describe higher correlation

and dissipative collision rates.

Without subband structure the multi-subband equation (12.27) reduces

to the two-band semiconductor Bloch equations (12.19). For compactness

of notation, we do not split Eq. (12.27) into separate equations for the oﬀ-

diagonal polarization components and the diagonal components (i = j, µ =

ν), which describe the density kinetics in the various subbands. Depending

on the selection rules and the spectral width of the exciting laser pulse, ﬁnite

polarization components can be induced for more than one pair of subbands.

As in the two-band semiconductor Bloch equations, the Coulomb exchange

terms generate nonlinear terms in the multi-subband equations.

12.3 Scattering Terms

All interaction eﬀects beyond the mean ﬁeld approximation are contained

in the scattering terms. In particular, these terms introduce dissipative

behavior in the form of dephasing rates for the interband polarization and

collision rates describing the relaxation of the electron and hole distribu-

tions. The relaxation kinetics drives the particle distribution toward ther-

January 26, 2004 16:26 WSPC/Book Trim Size for 9in x 6in b ook2

222 Quantum Theory of the Optical and Electronic Properties of Semiconductors

mal distributions often in times much shorter than the radiative lifetime of

the carriers.

A simple phenomenological description of the relaxation needs at least

two relaxation times, called T



and T

e,k



scatt

e,k

− n

e,k

(t)



−

e,k

(t)

, (12.28)

where f

e,k

=1/(e

−µ)β

+1)is the Fermi function of Chap. 6. Here, the

second term describes recombination of carriers whereas the ﬁrst term mod-

els the intraband relaxation, i.e., the relaxation of the general nonequilib-

rium distribution n

e,k

towards a quasi-equilibrium Fermi distribution f

e,k

leaving the total number of electrons in the conduction band unchanged.

Thus



e,k



e,k

(t)=N

(t) . (12.29)

This relation allows us to calculate the chemical potential µ

(T,N

(t)).A

reﬁned treatment would take into account that f

e,k

does not yet describe

the total equilibrium distribution, but only a local equilibrium f

e,k

(t) with

slowly varying chemical potential and temperature, and — more generally

— also with a slowly changing drift velocity. We will, however, not dwell

further on these phenomenological treatments, but ask how such a dissipa-

tive kinetics can be derived microscopically by coupling the electron system

to a bath with a continuous energy spectrum.

Before doing that, let us also brieﬂy consider the dephasing kinetics of

the interband polarization which describes the decay of quantum coherence

in a coherently excited system. The simplest description of dephasing uses

a dephasing time, also called a transverse relaxation time T

. This simple

phenomenological description of dephasing works surprisingly often reason-

ably well, given the complex underlying scattering kinetics. However, also

here, nonlinear and non-Markovian eﬀects set a limit to the simple phe-

nomenological ansatz.

In the low excitation regime, the dissipative kinetics is determined by

impurity scattering or in pure, polar III–V and II–VI compound semicon-

ductors by the scattering of the excited carriers with phonons. Of the

various diﬀerent phonon branches, the carrier scattering with longitudi-

nal optical (LO) phonons usually leads to the most rapid dynamics. At

high excitation levels, where a dense electron–hole plasma is generated,

the carrier–carrier collisions are the fastest dissipative processes. We treat

here the simpler case of LO-phonon scattering ﬁrst. In contrast to acoustic

January 26, 2004 16:26 WSPC/Book Trim Size for 9in x 6in b ook2

Semiconductor Bloch Equations 223

phonons with their linear dispersion, optical phonons have little dispersion

and can often simply be described by one energy ω

. Typical LO-phonon

energies in III–V and II–VI semiconductors are of the order of 20 to 40

meV.

The carriers are scattered within their bands by the absorption or emis-

sion of one LO phonon. The corresponding intraband scattering Hamilto-

nian, the so-called Fröhlich Hamiltonian, is given by:

e−LO



i,k,q

g

†

i,k+q

i,k

+ b

†

−q

, (12.30)

where b

and b

†

−q

are the bosonic phonon annihilation and creation opera-

tors, respectively. Note, that the momentum conservation is built into the

Fröhlich Hamiltonian. The analysis shows that as long as the energy spec-

trum of the electrons is continuous, the coupling to a bath of dispersionless

optical phonons will give rise to dissipation. Only in quantum dots, where

the carriers are conﬁned in all space dimensions so that no momentum can

be deﬁned, one has to take the dispersion of the LO-phonons into account

in order to get dephasing.

If the momentum transfer is neglected by setting q =0in the Fröhlich

interaction Hamiltonian, an exactly treatable model results because diﬀer-

ent electron momentum states are no longer coupled. Even though it is

based on additional assumptions, such an exactly treatable model is of con-

siderable interest to study carrier relaxation and dephasing for arbitrary

strengths of the coupling.

The interaction matrix element g

is given by

2





∞

−





, (12.31)

where V

is again the bare Coulomb matrix element and 

and 

∞

,re-

spectively, are the low and high frequency dielectric constants of the unex-

cited crystal. The Coulomb matrix element in (12.31) shows that eﬀective

carrier–carrier interaction mediated by the exchange of an LO phonon is

also of Coulombic nature. The screening of V

due to optical phonons with

the frequency ω

occurs between the low and high frequency limit. This

is the reason why the diﬀerence between 1/

∞

and 1/

determines the

interaction potential (see also problem 12.5).

It is usual, to deﬁne the strength of the LO-phonon coupling as the ratio

of phonon-induced electron energy shift to phonon energy in terms of the

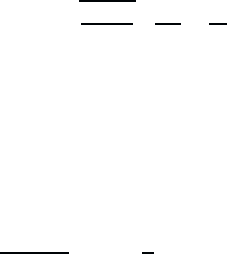
January 26, 2004 16:26 WSPC/Book Trim Size for 9in x 6in b ook2

224 Quantum Theory of the Optical and Electronic Properties of Semiconductors

dimensionless Fröhlich coupling parameter

= e



2





∞

−





. (12.32)

In the weakly polar III–V compounds, α

1, which justiﬁes the use of

perturbation theory in these materials. In the more polar II–VI compounds,

 1, which deﬁnes the intermediate polaron coupling regime. Here,

nonperturbative methods are needed.

We limit our discussion here to the weak coupling regime. The collision

term due to LO-phonon scattering is given by

∂ρ

i,j

(k)

∂t



scatt





e−LO

†

j,k

i,k

+ a

†

j,k

e−LO

i,k

]



= i



a

†

j,k+q

i,k

+ b

†

−q

−a

†

j,k

i,k−q

+ b

†

−q



= i



−

ij,k,q

+ F

ij,k,q

− G

−

ij,k,q

− G

ij,k,q

. (12.33)

We see, that the scattering term couples the two-operator dynamics to ex-

pectation values of two electron and one phonon operator. These quantities

are called phonon-assisted density matrices. In detail, the phonon-assisted

density matrices are

−

ij,k,q

= a

†

j,k+q

i,k



ij,k,q

= a

†

j,k+q

i,k

†

−q



−

ij,k,q

= a

†

j,k

i,k−q



ij,k,q

= a

†

j,k

i,k−q

†

−q

 . (12.34)

There are relations between the four phonon-assisted density matrices. F

−

and F

, and similarly G

−

and G

diﬀer only by the exchange of the phonon

annihilation and creation operators. Consequently, the phonon absorption

and emission processes in the − and + functions are interchanged, which

can simply be accomplished by a reversal of the phonon frequency and

momentum, as will be discussed later. Furthermore,

−

ij,k,q

= F

−

ij,k,q



k→k−q

and G

ij,k,q

= F

ij,k,q



k→k−q

, (12.35)

so only one phonon-assisted density matrix has to be evaluated explicitly.

Because we do not know the phonon-assisted density matrices, we write

down their equations of motion under the full Hamiltonian H = H

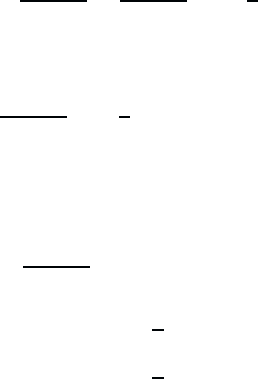
January 26, 2004 16:26 WSPC/Book Trim Size for 9in x 6in b ook2

Semiconductor Bloch Equations 225

+ H

e−LO

,whereH



ω

†

is the free phonon Hamiltonian.

The electron Hartree–Fock Hamiltonian can be written as



ij,k

†

i,k

j,k

, (12.36)

where the Hamilton matrix is given by

ij,k

= 

i,k

−



V (q)(ρ

ij,k−q

− δ

) −E(t)d

(k) , (12.37)

which includes the coupling to the coherent light ﬁeld. We will call H

= H

the mean-ﬁeld Hamiltonian.

The resulting equation of motion is

∂F

−

ij,k,q

∂t

∂F

−

ij,k,q

∂t









e−LO

†

j,k+q

i,k



 . (12.38)

The homogeneous mean-ﬁeld time development is given by

∂F

−

ij,k,q

∂t







−

il,k,q

lj,k+q

−H

il,k

−

lj,k,q

−

iω

+γ

ij,k,q

−

ij,k,q

(12.39)

or explicitly

∂F

−

ij,k,q

∂t



= i



j,k+q

− 

i,k

− ω

+ iγ

ij,k,q

−

ij,k,q

−



E(t)





−

il,k,q

(k + q) − d

(k)F

−

lj,k,q



−





(

−

il,k,q

V (q



)



(k + q − q



) − δ

l,v

j,v



− V (q



)



(k − q



) − δ



−

lj,k,q

)

. (12.40)

The ﬁrst line of (12.40) describes the free evolution of the phonon-assisted

density matrix F

−

. We have added an inﬁnitesimal damping γ

ij,k,q

to in-

sure an adiabatic switching on. The second line describes the Stark shifts

of the energy levels due to the laser light pulse, while the next two lines

describe the Hartree–Fock corrections. In total, Eq. (12.40) gives a homo-

geneous equation for the mean-ﬁeld development of F

−

. The second term

in Eq. (12.38), which has not been evaluated so far, gives rise to inhomoge-

neous terms in the form of new higher order density matrices. We decouple

January 26, 2004 16:26 WSPC/Book Trim Size for 9in x 6in b ook2

226 Quantum Theory of the Optical and Electronic Properties of Semiconductors

the resulting hierarchy of an inﬁnite series of equations of larger and larger

density matrices by factorization into single particle reduced density matri-

ces. Best insight in the physical nature of the resulting terms is obtained,

if we do not evaluate the commutator in (12.38) at all, but factorize the

products of four electron and two phonon operators directly:







e−LO

†

j,k+q

i,k



 (12.41)

= ig



(



(k)





− ρ



(k + q)



− (N

+1)ρ



(k + q)





− ρ



(k)



)

where N

=1/(e

βω

−1) = N(ω

) is the number of thermal LO phonons.

For simplicity, we consider the phonons as a thermal bath. Similar equa-

tions hold for the other three phonon-assisted density matrices.

12.3.1 Intraband Relaxation

Let us consider for the moment only diagonal density matrices

i,i

(k)=n

(k) (12.42)

and neglect corrections of the energy spectrum (i.e. lines 2 to 4 in (12.39)).

Under these simplifying conditions, Eq. (12.38) reduces to

∂F

−

ii,k,q

∂t

= i



i,k+q

− 

i,k

− ω

+ iγ

ii,k,q

−

ii,k,q

(

N(ω

(k,t)



1−n

(k+q,t)



−



N(ω

)+1



(k+q,t)



1−n

(k,t)



)

(12.43)

A formal integration yields

−

ii,k,q

(t)=ig



−∞





i,k+q

−

i,k

−ω

+iγ

ii,k,q

(t−t



)

(

N(ω

(k,t



)



1−n

(k + q,t



)



−



N(ω

)+1



(k+q,t



)



1−n

(k,t



)



)

. (12.44)

As already mentioned, the phonon-assisted density matrix F

can be ob-

tained from F

−

by interchanging phonon absorption and emission and re-

versing the phonon momentum. We introduce for this purpose the sign

January 26, 2004 16:26 WSPC/Book Trim Size for 9in x 6in b ook2

Semiconductor Bloch Equations 227

function σ = ±1 and replace ω

→ σω

and note that the following rela-

tions are valid:

σN(σω

σ=−1

= −

−βω

− 1

βω

− 1+1

βω

− 1

= N(ω

)+1 , (12.45)

and



N(σω

)+1





σ=−1

= N (ω

) . (12.46)

Using these relations, we formally introduce into the scattering rate (12.33)

asumoverσ:

∂n

(k)

∂t



scatt

= −



q,σ=±1

σg



−∞





i,k+σq

−

i,k

−σω

+iγ

ii,k,q

(t−t



)

(

N(σω

(k,t



)



1−n

(k + σq,t



)



−



N(σω

)+1



(k + σq,t



)



1−n

(k,t



)



)

−

(

k → k −σq

)

. (12.47)

The last term generates from the preceding ones the contributions of the

G functions.

The appearance of the time integral on the RHS of Eq. (12.47) shows

that in general the scattering rate depends on the history of the system.

In particular, the distribution functions enter into the scattering rate with

their values at earlier times t



≤ t. Processes with such a memory struc-

ture are called non-Markovian. They arise from the elimination of the

dynamics of the phonons and the higher correlations. Such non-Markovian

scattering integrals are typical for the short-time regime in which quantum

mechanical coherence of the electron and phonon states (here in the form

of the coherent exponential wave factors) is still present. Therefore, the

non-Markovian short-time dynamics is called quantum kinetics.Onlyfor

long times, the non-Markovian quantum kinetics reduces to the Markovian

scattering kinetics of Boltzmann.

Suppose that the particles are excited by a pulse around t =0.Ifthe

time t is long enough so that tω

# 1, the exponentials oscillate rapidly.

The distribution functions vary slowly compared to the exponentials and

can be taken out of the integral with their value at the upper boundary.

This is the so-called Markov approximation. The integrals over the remain-

ing exponentials then yield the energy conserving Dirac delta function times

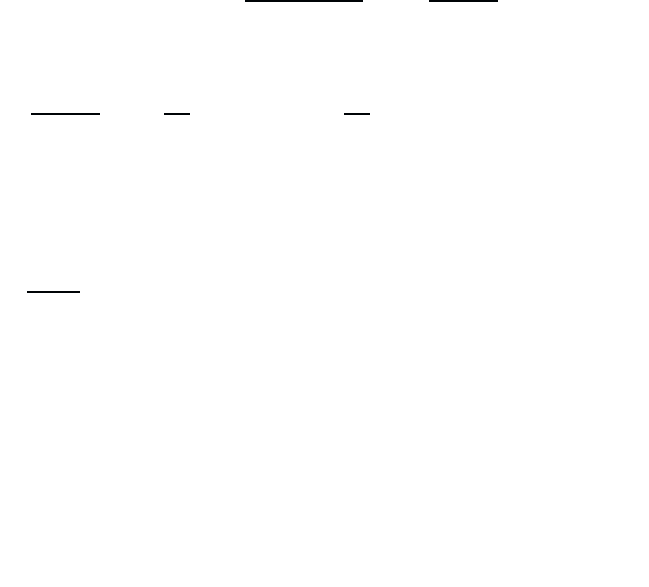
January 26, 2004 16:26 WSPC/Book Trim Size for 9in x 6in b ook2

228 Quantum Theory of the Optical and Electronic Properties of Semiconductors

afactorofπ. In detail, the time integral has the structure



−∞



i(∆+iγ)(t−t



)

i(∆+iγ)(t−t



)

−i(∆ + iγ)



−∞

∆ + iγ

. (12.48)

With Dirac’s identity we get

∆ + iγ

= i



∆

− iπδ(∆)



= iP

∆

+ πδ(∆) , (12.49)

where P denotes the principal value of the integral. Using this result in Eq.

(12.47), taking the real part, and evaluating the σ summation, we obtain

in this long-time limit the result:

∂n

(k)

∂t



scatt

= −



2πg



i,k+q

− 

i,k

− ω

(

(k,t)



1−n

(k+q,t)



−(N

+1 ) n

(k+q,t)



1−n

(k,t)



)

−



2πg



i,k−q

− 

i,k

+ ω

(

+1 ) n

(k,t)



1−n

(k−q,t)



−N

(k−q,t)



1−n

(k,t)



)

(12.50)

electron–phonon Boltzmann scattering rate

This is the famous Boltzmann scattering rate. It contains the transition

probabilities per unit time as determined by Fermi’s golden rule, compare

Fig. 12.1. The ﬁrst scattering rate describes an intraband electron transi-

tion from state i, k to state i, k + q by absorption of a phonon. For this

transition, one needs a phonon (the probability is given by N

), the initial

electron state has to be occupied (probability n

(k,t)) and the ﬁnal state

has to be empty (probability 1 − n

(k + q,t)). Due to this transition rate

the electron distribution at state i, k decreases (- sign). The next term de-

scribes the back-scattering from the initial state i, k + q with N

phonons

to the ﬁnal state i, k with N

+1phonons. This phonon emission process

takes place as stimulated and spontaneous emission. Thus one gets a factor

+1. For both described scattering processes, the energy before and

after the collision has to be conserved 

i,k+q

= 

i,k

+ ω

. In the following