Haug H., Koch S. Quantum theory of the optical and electronic properties of semiconductors

Подождите немного. Документ загружается.

January 26, 2004 16:26 WSPC/Book Trim Size for 9in x 6in b ook2

Excitons 189

Detuning D

exitons

Coulomb

enhancement

free carriers

E-4E

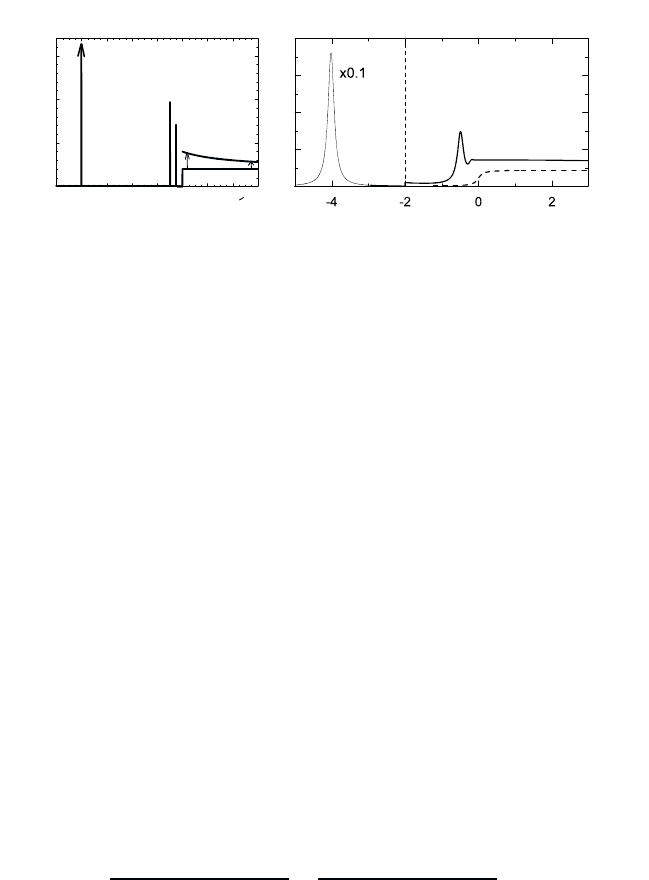
Fig. 10.3 Schematic (left ﬁgure) and calculated (right ﬁgure) band edge absorption

spectrum for a 2D semiconductor. Shown are the results obtained with and without

including the Coulomb interaction. The 1s-exciton part of the computed absorption

spectra has been scaled by a factor of 0.1 .

approaches 2 for ∆ → 0. The absorption at the band edge is thus twice

the free-carrier continuum absorption. For a ﬁnite damping, the absorption

of the ionized states and the absorption in the higher bound states again

join continuously. Fig. 10.3 shows both, the schematic and the computed

absorption spectrum using Eq. (10.110). In comparison to the 3D-case,

the 2D 1s-exciton is spectrally far better resolved as a consequence of the

four-fold increase in binding energy in 2D.

10.5.2 Quasi-One-Dimensional Case

In the ﬁnal subsection of this exciton chapter, we discuss the optical spectra

of quantum wires. Because of the cut-oﬀ in the Coulomb potential we have

for the optical susceptibility

χ(ω)=−2|d



(αγR)|



(ω + iδ) − E

− E

−

(ω + iδ)+E

+ E



. (10.112)

With the q1D eigenfunctions of the bound and ionized pair states,

Eqs. (10.75) and (10.97), respectively, we get the following resonant contri-

butions to the spectrum

January 26, 2004 16:26 WSPC/Book Trim Size for 9in x 6in b ook2

190 Quantum Theory of the Optical and Electronic Properties of Semiconductors

χ(ω)=−





λ,1/2

(2γR/λa

(ω + iδ) − E

− E



∞

π/x

2π

(2)

(1)

− D

(1)

(2)

(1)

+ |D

(2)

(ω + iδ) − E

− E



(10.113)

where x = a

k is used again as the integration variable in the contribution of

the continuum states. The functions D

(i)

and W

(i)

deﬁned in Eqs. (10.93)

and (10.91), respectively, are all evaluated at ζ =2ikγR. The absorption

spectrum is ﬁnally given by

α(ω)=

4πω





λ,1/2

(2γR/λa

πδ(∆ − E

)

πa

(2)

(1)

− D

(1)

(2)

(1)

+ |D

(2)

π/

√

∆

√

∆



, (10.114)

where ∆=(ω − E

)/E

is again the normalized energy detuning from

the band gap. The Sommerfeld factor which describes the deviations of the

Detuning D

E -xE

excitons

free carriers

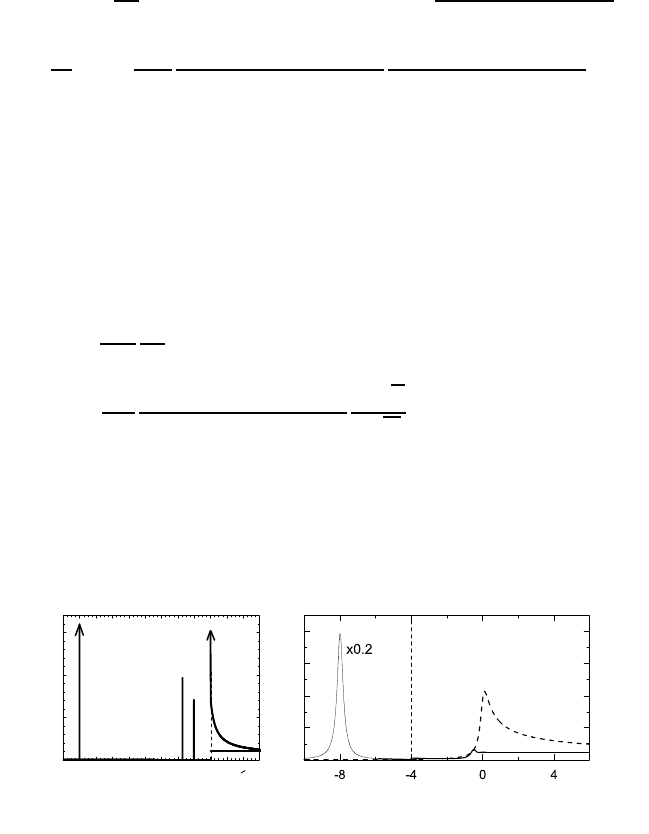
Fig. 10.4 Schematic (left ﬁgure) and calculated (right ﬁgure) band edge absorption

spectrum for a quasi-1D semiconductor. Shown are the results obtained with and with-

out including the Coulomb interaction. The 1s-exciton part of the computed absorption

spectra has been scaled by a factor of 0.2 .

January 26, 2004 16:26 WSPC/Book Trim Size for 9in x 6in b ook2

Excitons 191

continuum spectrum from the free-carrier spectrum in Chap. 5 is given by

C(ω)=

π/

√

∆

(2)

(1)

− D

(1)

(2)

(1)

+ |D

(2)

. (10.115)

In striking contrast to the 3D and 2D cases, the q1D Sommerfeld factor

C(ω) < 1 for all ω>E

. Due to this fact, the singular 1D-density of

states does not show up at all in the absorption spectrum (see Fig. 10.4).

In fact, the band gap in a quantum wire cannot be determined directly

from the low-intensity optical spectra, so that other techniques, such as

two-photon absorption, have to be used for such a measurement. The

absences of any structure at the band gap is by no means a consequence

of a ﬁnite broadening but solely a Coulomb eﬀect. A very large part of

the total oscillator strength is accumulated in the exciton ground state.

Note, that the ﬁrst excited state has odd parity, only the second excited

state contributes to the absorption spectrum. The approximate vanishing

of the higher bound states (10.80) shows that they have indeed very small

oscillator strengths.

REFERENCES

R.J. Elliott, in Polarons and Excitons, eds. C.G. Kuper and G.D. White-

ﬁeld, Oliver and Boyd, (1963), p. 269

L.D. Landau and E.M. Lifshitz, Quantum Mechanics, Pergamon, New York

(1958)

L.I. Schiﬀ, Quantum Mechanics,3rded., McGraw Hill, New York (1968)

M. Shinada and S. Sugano, J. Phys. Soc. Japan 21, 1936 (1966)

For further discussion of the theory of excitons see:

Polarons and Excitons, eds. C.G. Kuper and G.D. Whiteﬁeld, Oliver and

Boyd, (1963)

R.S. Knox, Theory of Excitons, Academic, New York (1963)

For the theory of excitons in quantum wires see:

R. Loudon, Am. J. Phys. 27, 649 (1959)

L. Banyai, I. Galbraith, C. Ell, and H. Haug, Phys. Rev. B36, 6099 (1987)

January 26, 2004 16:26 WSPC/Book Trim Size for 9in x 6in b ook2

192 Quantum Theory of the Optical and Electronic Properties of Semiconductors

T. Ogawa and T. Takagahara, Phys. Rev. B43, 14325 (1991)

PROBLEMS

Problem 10.1: Derive the Hamiltonian (10.14) from Eq. (7.29) by includ-

ing the band index λ with all the operators and by summing over λ = c, v.

Discuss the terms which have been omitted in (10.14).

Problem 10.2: Use the Heisenberg equation with the Hamiltonian (10.14)

to compute the equation of motion (10.18) for the interband polarization.

Make the Hartree–Fock approximation in the four-operator terms to obtain

Eq. (10.21).

Problem 10.3: Verify that Eqs. (10.105) and (10.110) correctly reduce

to the respective free-particle result without Coulomb interaction. Hint:

Formally one can let the Bohr radius a

→∞to obtain the free-particle

limit.

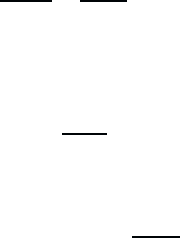
January 26, 2004 16:26 WSPC/Book Trim Size for 9in x 6in b ook2

Chapter 11

Polaritons

In direct-gap semiconductors, excitons and photons are strongly coupled.

To account for this coupling, it can be useful, especially in the linear regime,

to introduce new quasi-particles, the polaritons, which combine exciton

and photon properties. This polariton concept has been very helpful for

explaining optical measurements in 3D- semiconductors with a large direct

gap at low excitation densities.

11.1 Dielectric Theory of Polaritons

In Chap. 10, we derived the Wannier equation, Eq. (10.35), for the rela-

tive motion of an electron–hole pair. If we include also the center-of-mass

motion, this equation becomes

−





∇



∇

+ V (r)



ψ(R, r)=E

tot

ψ(R, r) , (11.1)

where M = m

+ m

. As in the case of the hydrogen atom, the center-of-

mass motion is described by a plane wave

ψ(R, r)=

ik·R

3/2

ψ(r) . (11.2)

Correspondingly, the total energy eigenvalue of Wannier excitons is

tot

= E

+ E



. (11.3)

As in the case of an hydrogen atom, the center-of-mass wave function of

the exciton is a plane wave ∝ exp(ik · R).

193

January 26, 2004 16:26 WSPC/Book Trim Size for 9in x 6in b ook2

194 Quantum Theory of the Optical and Electronic Properties of Semiconductors

photon dispersion

exciton dispersion

Fig. 11.1 Schematic drawing of photon and 1s-exciton dispersion.

In Fig. 11.1, we plot the dispersion of the 1s-exciton together with the

dispersion of the light

ω

ck

, (11.4)

where n

is the background refractive index of the medium. The ﬁgure

shows that both dispersions intersect, i.e., there is a degeneracy at the in-

tersection point. The exciton–photon interaction removes that degeneracy

introducing a modiﬁed joint dispersion. The quasi-particles associated with

this new dispersion are the exciton–polaritons. In general, polaritons are

also formed by transverse optical phonons and the light, called phonon–

polaritons. Since we do not discuss phonon–polaritons in this book, we

refer to the exciton–polaritons simply as polaritons.

The optical dielectric function for the excitons, i.e., without the ioniza-

tion continuum, is

(ω)=

[1 + 4πχ(ω)]

= 



1 − 8π|d



|ψ

(r =0)|

(ω + iδ) − E

− E



, (11.5)

where 

= n

and Eq. (10.103) have been used. In this form, only resonant

terms are contained and the momentum of the emitted or absorbed photon

has been neglected. In order to ﬁnd the propagating electromagnetic modes

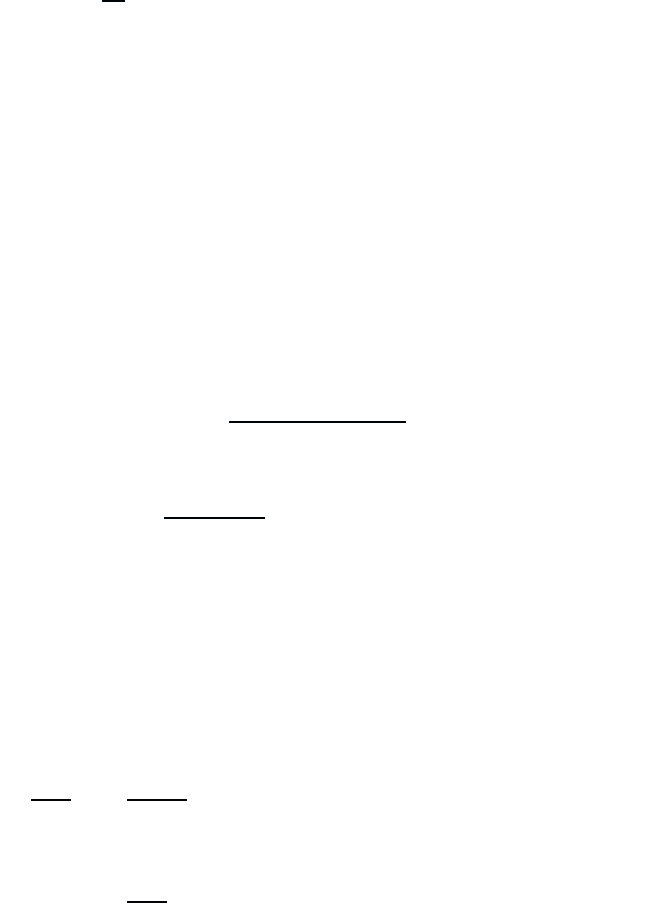
January 26, 2004 16:26 WSPC/Book Trim Size for 9in x 6in b ook2

Polaritons 195

in a dielectric medium, we have to insert (ω) into the wave equation (1.43)

for the transverse electric ﬁeld of a light beam. For a plane wave, we get



−k

(ω)



i(k·r−ωt)

=0 . (11.6)

The transverse eigenmodes of the medium are obtained from the require-

ment that E

=0,sothat

= ω

(ω) . (11.7)

transverse eigenmodes

11.1.1 Polaritons withou t Spatial Dispersion

and Damping

Let us analyze Eq. (11.7) considering only the contribution of the lowest

exciton level,

(ω)  



1 − 8π|d

|ψ

(r =0)|

(ω + iδ) − E

+ E



, (11.8)

(ω)=



1 −

∆

ω − ω

+ iδ



, (11.9)

where

∆=8π|d

|ψ

(r =0)|

and  ω

= E

− E

. (11.10)

In order to satisfy Eq. (11.7), the wave number k has to be chosen complex

k = k



+ ik



. (11.11)

Then we can write the real and imaginary part of Eq. (11.7) as





1 −

∆

ω − ω



= k

2

− k

2

(11.12)

and

πδ(ω − ω

)



=2k





, (11.13)

January 26, 2004 16:26 WSPC/Book Trim Size for 9in x 6in b ook2

196 Quantum Theory of the Optical and Electronic Properties of Semiconductors

respectively, where the Dirac identity, Eq. (1.17), has been used. The imag-

inary part of the wave number is proportional to δ(ω − ω

) describing ab-

sorption at the exciton resonance. Outside the resonance (ω = ω

) we

obtain the undamped polariton modes



ω − ω

− ∆

ω − ω



√



. (11.14)

The resulting dispersion is plotted in Fig. 11.2.

0 1 2 3

ww/

k' c/ nw

Fig. 11.2 Polariton dispersion without spatial dispersion for ∆/ω

=0.2.

From Eq. (11.14) one obtains for low frequencies, ω<<ω

, a photon-

like dispersion

ω 







(1 + ∆/ω

)

(11.15)

with a light velocity slightly smaller than c/n

.Forω → ω

,thewave

number diverges, k



→∞. No solution of Eq. (11.14) exists for frequencies

between ω

and ω

+∆. In other words, there is a stop band between ω

and ω

+∆separating the lower and upper polariton branch. At ω

+∆,



is zero and for ω>>ω

one again obtains a photon-like dispersion with

the light velocity c/n

The longitudinal eigenmodes of a dielectric medium are determined by

January 26, 2004 16:26 WSPC/Book Trim Size for 9in x 6in b ook2

Polaritons 197

(ω)=0 , (11.16)

longitudinal eigenmodes

which yields the eigenfrequencies of the longitudinal exciton ω

= ω

+∆,

while the transverse exciton frequency ω

= ω

. Therefore, ∆ is called the

longitudinal-transverse (LT) splitting.

For the longitudinal excitons, the polarization is parallel to the wave

vector k. Eq. (11.10) shows that the longitudinal-transverse splitting is

proportional to the so-called optical matrix element

|ψ

(r =0)|

∝

, (11.17)

where Eqs. (10.70) and (10.71) have been used. The region in which no

transverse waves propagate is thus particularly large for crystals with small

exciton Bohr radii, i.e., in wide-gap semiconductors such as CuCl. Whether

the LT-splitting can be observed experimentally depends on the ratio of

∆ to the exciton damping δ, which is ﬁnite in real crystals, e.g., as a

consequence of the exciton–phonon interaction. For ∆ >> δ,thestop

band is physically important, but not for ∆ << δ.

In general, the dielectric functions for longitudinal and transverse ex-

citations are not the same. However, they become degenerate in the long

wave-length limit, which we have considered so far. For more details see

Haug and Schmitt–Rink (1984).

11.1.2 Polaritons with Spatial Dispersion and Damping

If the momentum of the photon is not disregarded, the momentum conser-

vation requires that the created or annihilated exciton has the same ﬁnite

wave vector as the photon. The energy of an exciton with a ﬁnite transla-

tional momentum k is given by Eq. (11.3). Then the transverse dielectric

function becomes wave-number-dependent, yielding for the 1s-exciton state

(k,ω)=



1 −

∆

ω − ω

−

k

+ iγ



. (11.18)

Here, we treat the damping γ as a generally nonvanishing constant. How-

ever, we note that a realistic description of an exciton absorption line often

January 26, 2004 16:26 WSPC/Book Trim Size for 9in x 6in b ook2

198 Quantum Theory of the Optical and Electronic Properties of Semiconductors

requires a frequency-dependent damping γ(ω).Aconstantγ results in a

Lorentzian absorption line, but in reality one observes at elevated temper-

atures nearly universally an exponential decrease of the exciton absorption

α(ω) for frequencies below the exciton resonance, i.e.,

α(ω)=α

−(ω

−ω)/σ

for ω<ω

. (11.19)

Urbach rule

The derivation of the Urbach rule needs a damping γ(ω) which decreases

with increasing detuning ω

− ω. The physical origin of the dynamical or

frequency-dependent damping is the following: the absorption of a photon

with insuﬃcient energy ω<ω

requires the scattering of the virtually

created exciton with energy ω into a state E

= ω

+

/2M under the

absorption or scattering of an already present excitation in the crystal. In

polar semiconductors, the relevant excitation will be a longitudinal optical

(LO) phonon. Now it is evident that γ(ω) decreases rapidly with decreasing

frequency because the probability to absorb n LO phonons decreases rapidly

with increasing n. From a microscopic point of view, the damping is the

imaginary part of the exciton self-energy Σ(k,ω), which in general is both

frequency- and momentum-dependent.

Now let us return to the simple form of Eq. (11.18) to discuss the

transverse eigenmodes. Because a momentum-dependent dielectric func-

tion means a nonlocal response in real space, one speaks in this case also

of a dielectric function with spatial dispersion. Inserting Eq. (11.18) into

the eigenmode equation (11.7) yields



= ω



1 −

∆

ω − ω

−

k

+ iγ



. (11.20)

The solution of this equation for the real and imaginary part of the wave

number is shown in Fig. 11.3.

With spatial dispersion and ﬁnite damping one ﬁnds for all frequencies two

branches, ω

and ω

. At high frequencies, ω/ω

> 1, Fig. 11.3 again shows a

photon-like and an exciton-like branch. In the range of the LT-split, ω



)

has some structure which results in a negative group velocity [negative slope

of ω



)]. One sees, however, that in this range the damping of this mode

increases strongly. In a region with damping, the group velocity loses its