Haug H., Koch S. Quantum theory of the optical and electronic properties of semiconductors
Подождите немного. Документ загружается.


January 26, 2004 16:26 WSPC/Book Trim Size for 9in x 6in b ook2
Excitonic Optical Stark Effect 249
t
t
+
t
t
−
dt
∂w
λ
∂t
= w
λ
(t
t
+
) − w
λ
(t
t
−
)
−i
2d
cv
e
−ik
t
·r
E
t
p
∗
λ
(t
t
−
)+i
2d
∗
cv
e
ik
t
·r
E
∗
t
p
λ
(t
t
−
)+... , (13.65)
wherewedenotebyt
t
−
and t
t
+
the times just before and after the probe
pulse, respectively. In Eq. (13.65), we used
p
λ
(t
t
)=p
λ
(t
t
−
)+O(E
t
) , (13.66)
where the correction term of order E
t
has been neglected, since we are
interested only in terms linear in E
t
. The expression for p
λ
(t
t
−
) is given by
Eq. (13.64). Inserting Eq. (13.65) into Eq. (13.64) shows that a grating
∝ e
i(k
t
−k
p
)·r
(13.67)
is formed in the sample. Light from the pump pulse can scatter from the
grating into the direction of the probe and can therefore be seen by the
detector. In addition, the probe transmission is also modified through the
saturation of the transitions.
To include all effects systematically, we now solve Eqs. (13.60) and
(13.61) for the polarization and density variables by expanding them in
powers of the fields
p
λ
(t)=i
d
cv
t
−∞
dt
e
−
i(
λ
−Ω)+γ
(t−t
)
E
p
(t
)e
−ik
p
·r
+ E
t
(t
)e
−ik
t
·r
w
λ
(t
)
i
d
cv
E
t
e
−ik
t
·r
e
−
i(
λ
−Ω)+γ
(t−t
t
)
w
λ
(t
t
−
)Θ(t − t
t
)
+ i
d
cv
t
−∞
dt
e
−
i(
λ
−Ω)+γ
(t−t
)
E
p
(t
)w
λ
(t
)e
−ik
p
·r
(13.68)
and

January 26, 2004 16:26 WSPC/Book Trim Size for 9in x 6in b ook2
250 Quantum Theory of the Optical and Electronic Properties of Semiconductors
w
λ
(t)=1−
i2d
cv
t
−∞
dt
e
−Γ(t−t
)
E
p
(t
)e
−ik
p
·r
+ E
t
(t
)e
−ik
t
·r
p
∗
λ
(t
)
+ i
2d
∗
cv
t
−∞
dt
e
−Γ(t−t
)
E
∗
p
(t
)e
ik
p
·r
+ E
∗
t
(t
)e
ik
t
·r
p
λ
(t
)
1 − i
2d
cv
e
−Γ(t−t
t
)
E
t
e
−ik
t
·r
p
∗
λ
(t
t
−
)Θ(t − t
t
)
+ i
2d
∗
cv
e
−Γ(t−t
t
)
E
∗
t
e
ik
t
·r
p
λ
(t
t
−
)Θ(t − t
t
)
− i
2d
cv
t
−∞
dt
e
−Γ(t−t
)
E
p
(t
)p
∗
λ
(t
)e
−ik
p
·r
+ i
2d
∗
cv
t
−∞
dt
e
−Γ(t−t
)
E
∗
p
(t
)p
λ
(t
)e
ik
p
·r
, (13.69)
where we used Eq. (13.62) for the probe pulse. Now, we insert Eq. (13.69)
into Eq. (13.68) and solve the resulting integral equation iteratively. This
way, we obtain many terms, most of which do not contribute to our final
result. In order to keep our equations as short as possible, we write only
those terms which lead to a contribution in the final result that influences
the probe transmission. We obtain
p
λ
(t)=
id
cv
E
t
e
−ik
t
·r
e
−[i(
λ
−Ω)+γ](t−t
t
)
w
λ
(t
t
−
)Θ(t − t
t
)
+2
d
2
cv
2
E
t
e
−i(k
t
+k
p
)·r
p
∗
λ
(t
t
−
)
t
t
t
dt
e
−[i(
λ
−Ω)+γ](t−t
)
e
−Γ(t
−t
t
)
E
p
(t
)Θ(t − t
t
)
−2
|d
cv
|
2
2
t
−∞
dt
e
−[i(
λ
−Ω)+γ](t−t
)
E
p
(t
)
t
−∞
dt
e
−Γ(t
−t
)
E
∗
p
(t
)p
λ
(t
)
+ ... . (13.70)
The third line of this expression is of the order (E
p
)
2
and contains an integral
over p
λ
. Since we keep only terms up to the order E
t
(E
p
)
2
in our analysis,
it is sufficient to solve this integral by inserting the first line of Eq. (13.70)
and the first term of Eq. (13.69) to get
January 26, 2004 16:26 WSPC/Book Trim Size for 9in x 6in b ook2
Excitonic Optical Stark Effect 251
p
λ
(t)=i
d
cv
E
t
e
−ik
t
·r
e
−[i(
λ
−Ω)+γ](t−t
t
)
w
λ
(t
t
−
)Θ(t − t
t
)
+2
d
2
cv
2
E
t
e
−i(k
t
+k
p
)·r
p
∗
λ
(t
t
−
)
×
t
t
t
dt
e
−[i(
λ
−Ω)+γ](t−t
)
e
−Γ(t
−t
t
)
E
p
(t
)Θ(t − t
t
)
− i
2d
cv
|d
cv
|
2
2
E
t
e
−ik
t
·r
t
t
t
dt
e
−[i(
λ
−Ω)+γ](t−t
)
E
p
(t
)
×
t
t
t
dt
e
−Γ(t
−t
)
E
∗
p
(t
) e
−[i(
λ
−Ω)+γ](t
−t
t
)
Θ(t − t
t
)
+ ... . (13.71)
At the end of our calculations, we are interested in the optical susceptibility
χ
λ
(ω) for the probe pulse. Therefore, we study the Fourier transform of
the polarization
P
λ
(ω)=
∞
−∞
dt e
iωt
P
λ
(t)=
∞
−∞
dt e
i(ω−Ω)t
p
λ
(t)
=
∞
t
t
dt e
i(ω−Ω)t
p
λ
(t)=
∞
0
dt e
i(ω−Ω)t
p
λ
(t + t
t
) e
−i(ω−Ω)t
t
. (13.72)
Here, we used the result of Eq. (13.71), that p
λ
(t) has a component pro-
portional to e
(ik
t
·r)
, (13.63), only for t>t
t
, i.e., after the probe hit the
sample. For the spectrum of the probe (test) pulse, we can write
E
t
(ω)=
∞
−∞
dt E
t
(t) e
iωt
=
∞
−∞
dt E
t
(t) e
i(ω−Ω)t
e
−ik
t
·r
E
t
e
i(ω−Ω)t
t
e
−ik
t
·r
(13.73)
Using Eqs. (13.66) and (13.71) – (13.73), we obtain
January 26, 2004 16:26 WSPC/Book Trim Size for 9in x 6in b ook2
252 Quantum Theory of the Optical and Electronic Properties of Semiconductors
P
λ
(ω)=i
d
cv
E
t
(ω)
γ − i(ω −
λ
)
,
w
λ
(t
t
−
)
− i
2d
cv
e
−ik
p
·r
p
∗
λ
(t
t
−
)
∞
0
dt
e
[i(ω− Ω)−Γ]t
E
p
(t
+ t
t
)
− 2
|d
cv
|
2
2
∞
0
dt e
i(ω−Ω)t
E
p
(t + t
t
)
×
t
0
dt
e
−Γ(t−t
)
e
−[i(
λ
−Ω)+γ]t
E
∗
p
(t
+ t
t
)
-
≡ χ
λ
(ω)E
t
(ω) . (13.74)
Extracting the probe susceptibility, we find
χ
λ
(ω)=i
d
cv
1
γ − i(ω −
λ
)
,
w
λ
(t
t
−
)
−2
|d
cv
|
2
2
t
t
−∞
dt
e
i(
λ
−Ω)−γ
(t
t
−t
)
E
∗
p
(t
)
∞
0
dt e
i(ω−Ω)−Γ
t
E
p
(t + t
t
)
−2
|d
cv
|
2
2
∞
0
dt e
i(ω−Ω)t
E
p
(t+t
t
)
t
0
dt
e
−Γ(t−t
)
e
−
i(
λ
−Ω)+γ
t
E
∗
p
(t
+t
t
)
-
(13.75)
where Eq. (13.64) has been used for p
∗
λ
(t
t
−
). The last term in Eq. (13.75)
canalsobewrittenintheform
−2
|d
cv
|
2
2
∞
0
dt
∞
t
dt e
i(ω−Ω)t
E
p
(t + t
t
) e
−Γ(t−t
)
e
−
i(
λ
−Ω)+γ
t
E
∗
p
(t
+ t
t
)
= −2
|d
cv
|
2
2
∞
0
dt
∞
0
dte
i(ω−Ω)t
e
−Γt
e
−
i(
λ
−ω)+γ
t
E
p
(t + t
+ t
t
)E
∗
p
(t
+ t
t
)
−2
|d
cv
|
2
2
1
Γ − i(ω − Ω)
∞
0
dt e
−
i(
λ
−ω)γ
t
|E
p
(t + t
t
)|
2
−i 2
|d
cv
|
2
2
1
ω − Ω
∞
0
dt e
−
i(
λ
−ω)+γ
t
|E
p
(t + t
t
)|
2
. (13.76)
January 26, 2004 16:26 WSPC/Book Trim Size for 9in x 6in b ook2
Excitonic Optical Stark Effect 253
Taking
λ
= ω
x
,withω
x
denoting the exciton resonance frequency, we can
use Eq. (13.76) to discuss the excitonic optical Stark effect. In order to see
the light-induced shift more clearly, we consider the large detuning case,
|ω − Ω| >> γ , |ω −
λ
| .
Inserting Eq. (13.76) into Eq. (13.75), we obtain the asymptotic behavior
as
δχ
λ
(ω) 2
d
cv
|d
cv
|
2
2
1
ω − Ω
∞
0
dt
e
−[i(
λ
−ω)+γ]t
γ − i(ω −
λ
)
|E
p
(t + t
t
)|
2
(13.77)
and for the pump-induced absorption change we get
δα(ω)=−Im
d
∗
cv
δχ
λ
(ω)
=
|d
cv
|
4
4
2
Ω −
λ
Im
∞
0
dt
e
−
i(
λ
−ω)+γ
t
γ − i(ω −
λ
)
|E
p
(t + t
t
)|
2
. (13.78)
To analyze Eq. (13.78), let us assume for a moment that we excite the
sample by a cw-beam, i.e., E
p
(t)=E
p
=const. Then we obtain from
Eq. (13.78)
δα(ω) ∝−
|E
p
|
2
e − Ω
p
2γ(
λ
− ω)
(
λ
− ω)
2
+ γ
2
2
(13.79)
which describes the absorption change caused by the shift of a Lorentzian
resonance. This can be seen by looking at
γ
γ
2
+(
λ
− ω − δ)
2
−
γ
γ
2
+(
λ
− ω)
2
−
2δγ(
λ
− ω)
γ
2
+(
λ
− ω)
2
2
, (13.80)
whereweassumedδ<<|
λ
− ω|. Hence, Eq. (13.79) yields a dispersive
shape around the resonance, ω =
λ
, which describes decreasing and in-
creasing absorption below and above the resonance, respectively.
For the case of pulsed excitation, the sample response is much more
complex. Inserting the full Eq. (13.75) into the first line of Eq. (13.78), we
obtain the results in Fig. 13.5 for different pump–probe delays. Fig. 13.5
shows, that for negative time delays, t
t
< 0, i.e., when the probe pulse
comes before the pump pulse maximum, the probe-transmission change
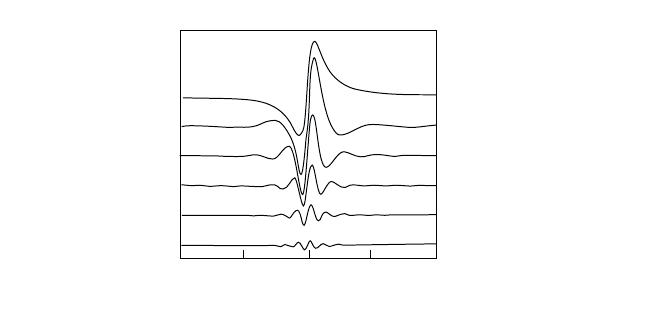
January 26, 2004 16:26 WSPC/Book Trim Size for 9in x 6in b ook2
254 Quantum Theory of the Optical and Electronic Properties of Semiconductors
-10
-5
0
5
10
Normalized Detuning
Differential Absorption
Fig. 13.5 Differential absorption spectra calculated in the spectral vicinity of the exciton
resonance
λ
= ω
x
. The detuning is defined as (ω − ω
x
)/σ,whereσ
−1
is the temporal
width of the pump pulse. The FWHM of the pump pulse was assumed to be 120 fs, and
the central pump frequency was detuned -10 below the resonance. The different curves
are for different pump–probe delays t
t
with 100 fs intervals, starting from the bottom
at -500 fs (probe before pump) to the top curve which is for 0 fs (pump–probe overlap).
[After Koch et al. (1988).]
shows oscillatory structures which evolve into the dispersive shape of the
optical Stark effect.
Similar oscillations are obtained for the case of resonant interband ex-
citation (Koch et al., 1988). In this situation, the pump laser is tuned into
the spectral regime of interband absorption, coupling an entire region of
electron–hole transitions. The spectral extent of this region is given by
the spectral width of the pump pulse. For negative pump–probe delays,
the femtosecond experiments also show transient transmission oscillations.
In contrast to the optical Stark effect, however, these oscillations then de-
velop into a symmetric feature, called the spectral hole, which describes the
saturation of the pump-laser coupled electron–hole transition.
The general origin of the transient transmission oscillations is found in
the grating, Eq. (13.67), which scatters parts of the pump pulse into the
direction of the probe pulse. For t<t
t
, the scattered pump interferes with
the probe and causes the oscillations. Alternatively, one can also view the
transient oscillations as perturbed free induction decay. The probe pulse
excites the polarization, which decays on the time scale of the coherence de-
cay time. The pump pulse then modifies the medium and perturbs (shifts)
the resonances, thus leading to the interference oscillations. For more de-

January 26, 2004 16:26 WSPC/Book Trim Size for 9in x 6in b ook2
Excitonic Optical Stark Effect 255
tails, see the review article by Koch et al. (1988) and the given references.
13.3 Correlation Effects
In this section, we go beyond the limit of extremely low intensities. This
makes it necessary to include in the semiconductor Bloch equations not
only the pure Hartree–Fock terms but also the leading contributions of the
correlation terms. In order to have a systematic approach, we go back to
the Coulomb part of the many-body Hamiltonian, Eq. (12.6), where we now
add extra summations over different electron (e, e
) and hole (h, h
)states
H
C
=
1
2
k,k
,q=0,e,e
V
q
α
†
e,k+q
α
†
e
,k
−q
α
e
,k
α
e,k
+
1
2
k,k
,q=0,h,h
V
q
β
†
h,k+q
β
†
h
,k
−q
β
h
,k
β
h,k
−
k,k
,q=0,e,h
V
q
α
†
e,k+q
β
†
h,k
−q
β
h,k
α
e,k
. (13.81)
Similarly, the interaction between the carriers and the classical electro-
magnetic field, H
I
, is generalized to
H
I
= −E(t) ·
k,e,h
d
eh
α
†
e,k
β
†
h,−k
+(d
eh
)
∗
β
h,−k
α
e,k
, (13.82)
with the electron–hole interband dipole matrix element d
eh
. In our analysis,
we explicitly include the heavy-hole valence band and the lowest conduction
band, both of which are twofold spin-degenerate. The two heavy-hole bands
(h =1, 2) are characterized by the states |−3/2,h>and |3/2,h>,and
the conduction bands (e =1, 2)by|−1/2,e>and |1/2,e>, respectively.
For light propagating in the z-direction, i.e., perpendicular to the plane
of the quantum well, we use the usual circularly polarized dipole matrix
elements
d
11
= d
0
σ
+
=
d
0
√
2
1
i
,
d
12
= d
21
=0 ,
d
22
= d
0
σ
−
=
d
0
√
2
1
−i
, (13.83)

January 26, 2004 16:26 WSPC/Book Trim Size for 9in x 6in b ook2
256 Quantum Theory of the Optical and Electronic Properties of Semiconductors
where d
0
is the modulus of d
11
and d
22
. Due to these selection rules, i.e.,
d
eh
∝ δ
eh
, we have two separate subspaces of optical excitations, that are
optically isolated. They are, however, coupled by the many-body Coulomb-
interaction, since it is independent of the band indices (spin).
As in Chap. 12, we evaluate the Heisenberg equation for the different
operator combinations to obtain
i
∂
∂t
P
eh
k
= −
&
E
e
k
+ E
h
k
'
P
eh
k
+
q=0
V
q
P
eh
k−q
+
d
eh
−
e
f
ee
k
d
e
h
−
h
d
eh
f
h
h
k
· E
−
q=0,k
,e
V
q
$3
α
†
e,k
α
†
e
,k
β
†
h,k+q
α
e
,k
−q
4
−
3
α
†
e,k+q
α
†
e
,k
β
†
h,k
α
e
,k
+q
4%
+
q=0,k
,h
V
q
$3
α
†
e,k+q
β
†
h
,k
+q
β
†
h,k
β
h
,k
4
−
3
α
†
e,k
β
†
h
,k
+q
β
†
h,k−q
β
h
,k
4%
. (13.84)
In the two-band case, i.e., if only a single conduction and a single valence
band is considered, we have e = e
=1and h = h
=1in Eq. (13.84). In the
more general multiband configuration, summations over all the respective
bands have to be considered. Since we restrict the analysis in this section
to transitions from heavy-holes to the lowest conduction band, P
eh
k
is non-
vanishing only for e = h =1and e = h =2, i.e., concerning the subband
indices it is proportional to δ
eh
, since the terms with e = h have no sources.
For similar reasons, also f
ee
k
and f
h
h
k
are diagonal, i.e., proportional to δ
ee
and δ
hh
, respectively.
In order to deal with the four-operator correlations that appear in
Eq. (13.84), we follow an approach where the nonlinear optical response
is classified according to an expansion in powers of the applied field. Stahl
and coworkers (1994) were the first who recognized that this traditional
nonlinear optics expansion establishes a systematic truncation scheme of
the Coulombic many-body correlations for purely coherent optical excita-
tion configurations. In the following, we outline the basic steps that are
involved in this procedure.
Studying the structure of the coupled equations for the correlation func-
tions, one finds that the four-operator terms which appear in the equation
January 26, 2004 16:26 WSPC/Book Trim Size for 9in x 6in b ook2
Excitonic Optical Stark Effect 257
of motion for the microscopic polarization can be decomposed into
3
α
†
e,k
α
†
e
,k
β
†
h
,k
α
e
,k
4
=
ˆ
k,
ˆ
h
3
α
†
e,k
α
†
e
,k
β
†
h
,k
β
†
ˆ
h,
ˆ
k
43
β
ˆ
h,
ˆ
k
α
e
,k
4
+O(E
5
) , (13.85)
where
3
α
†
e,k
α
†
e
,k
β
†
h
,k
β
†
ˆ
h,
ˆ
k
4
can be considered as an unfactorized product
of polarization operators that is of second order in the field, ∝O(E
2
) since
two electron–hole pairs are created, whereas
3
β
ˆ
h,
ˆ
k
α
e
,k
4
is linear in the
field, ∝O(E) since a single electron–hole pair is destroyed. Hence, the
right hand side of Eq. (13.85) is at least of third order in the field.
The correctness of this decoupling scheme can be verified quite easily,
whereas one needs more general considerations to obtain the explicit ex-
pressions. In the most straightforward way, one first notes that Eq. (13.85)
is valid when the semiconductor is in its ground state, since in this case
both sides vanish. Then one can take the time derivative of the lowest
(third) order contributions of Eq. (13.85) which are given by
5
∂
∂t
(α
†
e,k
α
†
e
,k
β
†
h
,k
α
e
,k
)
6
=
ˆ
k,
ˆ
h
5
∂
∂t
(α
†
e,k
α
†
e
,k
β
†
h
,k
β
†
ˆ
h,
ˆ
k
)
6
3
β
ˆ
h,
ˆ
k
α
e
,k
4
+
ˆ
k,
ˆ
h
3
α
†
e,k
α
†
e
,k
β
†
h
,k
β
†
ˆ
h,
ˆ
k
4
5
∂
∂t
(β
ˆ
h,
ˆ
k
α
e
,k
)
6
. (13.86)
Computing the time derivatives by evaluating the commutators with the
Hamiltonian according to the Heisenberg equation, inserting the obtained
equations of motion up to the required order in the field, and performing
the summations, Eq. (13.86) and thus Eq. (13.85) are readily verified.
Another, even simpler example for such a decoupling in a fully coherent
situation is the expression for the occupation probabilities in terms of the
microscopic polarizations up to second order in the field
f
ee
k
=
h
(P
eh
k
)
∗
P
e
h
k
+ O(E
4
) ,
f
hh
k
=
e
(P
e
h
k
)
∗
P
e
h
k
+ O(E
4
) . (13.87)
Analogous to what has been said above, also this conservation law, which
is nothing but the expansion of Eq. (13.9), can be verified by computing
January 26, 2004 16:26 WSPC/Book Trim Size for 9in x 6in b ook2
258 Quantum Theory of the Optical and Electronic Properties of Semiconductors
the time derivative and inserting the expressions up to the required order.
Instead of just merely verifying the decouplings in Eqs. (13.85) and
(13.87), we address the coherent dynamics of a many-body system on the
level of a general analysis. Let us start by defining a normally ordered
operator product as
{N,M}≡c
†
(ϕ
N
) c
†
(ϕ
N−1
) ... c
†
(ϕ
1
) c(ψ
1
) ... c(ψ
M−1
) c(ψ
M
) , (13.88)
where depending on ϕ
i
and ψ
j
the operators c
†
and c are electron or hole
creation or annihilation operators for certain k
i
and k
j
, respectively. The
quantities {N,M} contain the full information about the dynamics of the
photoexcited system. E.g., the microscopic polarization P
eh
k
corresponds
to {0, 2}, its complex conjugate (P
eh
k
)
∗
corresponds to {2, 0},andtheoc-
cupation probabilities f
aa
k
to {1, 1}.
Next, we consider the time derivative of the normally ordered operator
products, which is given by
6
5
4
3
2
1
123456
M
N
0
2
2
3
3
3
123
1
23
3
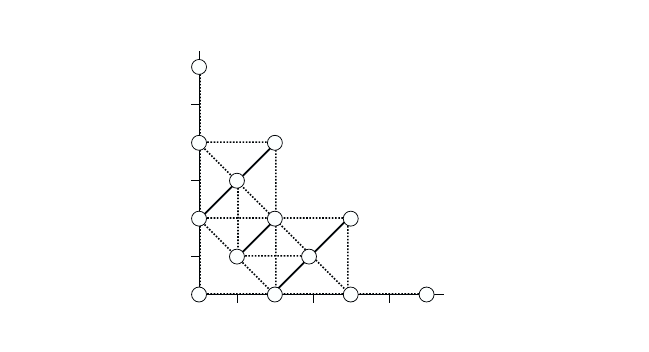
Fig. 13.6 Sketch of the coupling between dynamical variables, ({N, M}).Thenum-
bers in the circles denote the minimum order of the corresponding expectation value
< {N, M} > in the external field amplitude. The dotted (solid) lines symbolize the
optical (Coulomb) coupling. [After Lindberg et al. (1994).]
