Haug H., Koch S. Quantum theory of the optical and electronic properties of semiconductors
Подождите немного. Документ загружается.

January 26, 2004 16:26 WSPC/Book Trim Size for 9in x 6in b ook2
Excitonic Optical Stark Effect 239
Solving Eqs. (13.6) and (13.9) adiabatically, i.e., neglecting all possible
slow amplitude variations, we find for E(t)=E
p
exp(−iω
p
t)
P
k
=
(1 − 2n
k
)ω
R,k
e
k
− ω
p
. (13.10)
Eq. (13.10) together with Eqs. (13.7) - (13.9) form a complicated system of
nonlinear integral equations, which can be solved numerically or which has
to be simplified by further approximations.
In experiments, one usually applies a weak test beam to measure the
effects which the strong pump beam introduces in the semiconductor.
To study this situation, we add to the pump beam a weak test beam
E
t
exp(−iω
t
t) which induces an additional small polarization δP
k
.Lin-
earizing Eqs. (13.6) - (13.9) yields
i
d
dt
δP
k
= δe
k
P
k
+ e
k
δP
k
+2δn
k
ω
R,k
− (1 − 2n
k
) δω
R,k
, (13.11)
where
δe
k
= −
2
k
V
k−k
δn
k
, (13.12)
δn
k
=
P
k
δP
∗
k
+ P
∗
k
δP
k
1 − 2n
k
, (13.13)
and
δω
R,k
= d
cv
E
t
e
−iω
t
t
+
k
V
k−k
δP
k
. (13.14)
We now eliminate the time dependence of the pump field by splitting off a
factor exp(−iω
p
t) of P
k
, δP
k
and ω
R,k
, e.g., P
k
= p
k
exp(−iω
p
t).Thisway
we obtain
i
d
dt
δp
k
= δe
k
p
k
+(e
k
− ω
p
)δp
k
+2δn
k
ω
R,k
− (1 −2n
k
)δω
R,k
, (13.15)
where we redefined the change in the Rabi frequency as
δω
R,k
→ δω
R,k
= d
cv
E
t
e
i∆t
+
k
V
k−k
δp
k
, (13.16)
and ∆=ω
p
− ω
t
is the frequency difference of the pump and test beam.
This system of equations can be solved if the solutions of P
k
and n
k
under

January 26, 2004 16:26 WSPC/Book Trim Size for 9in x 6in b ook2
240 Quantum Theory of the Optical and Electronic Properties of Semiconductors
the influence of the strong pump beam alone are known. For a stationary
problem, we have to choose the form
δp
k
= δp
+
k
e
+i∆t
+ δp
−
k
e
−i∆t
. (13.17)
Once δp
+
k
is known, we get the susceptibility and the absorption spectrum of
the test beam in the usual way. In particular, one is interested to see how the
exciton absorption spectrum is influenced by a pump beam which is detuned
far below the lowest exciton resonance. In order to get a realistic absorption
spectrum, one takes a finite damping for polarization δP
k
induced by the
test beam into account. Note again, that a purely coherent equation for
the P
k
induced by the pump-beam, and a dissipative equation for δP
k
are a
physically justified model, because of the rapidly decreasing damping with
increasing detuning, i.e., the frequency-dependent dephasing. In Fig. 13.3,
we show the results of a numerical evaluation of the stationary equation
for a quasi-two-dimensional GaAs quantum-well structure. The detuning
of the pump beam with respect to the 1s-exciton was chosen as ten exciton
Rydberg energies. Fig. 13.3 clearly shows a large blueshift of the exciton
resonance with increasing pump intensity. Simultaneously also a blueshift of
the band edge occurs and the exciton oscillator strength does not decrease.
60
50
40
30
20
10
0
-4
-3
-2 -1
0
1
Absorption
Normalized Detuning
Fig. 13.3 Calculated 2D absorption spectrum versus normalized detuning (ω−E
G
)/E
0
according to Ell et al. for (E
g
− ω
p
)/E
0
=10and the pump intensities I
p
=0,7.5,
and 30 MW/cm
2
from left to right.
In order to analyze these numerical results, we analytically solve the
equations in first order of the pump intensity. Thus E
p
, P
k
,andn
k
can be

January 26, 2004 16:26 WSPC/Book Trim Size for 9in x 6in b ook2
Excitonic Optical Stark Effect 241
considered as small expansion parameters. From Eq. (13.9) we find
n
k
= |P
k
|
2
+ O(|P
k
|
4
) . (13.18)
The quasi-stationary equation for the polarization induced by the test beam
reduces with δp
+
k
>> δp
−
k
to (see problem 13.3)
k
H
0
kk
+∆H
kk
− (ω
t
+ iδ)δ
kk
δp
+
k
=(1− 2|p
k
|
2
)d
cv
E
t
, (13.19)
where H
0
is the unperturbed pair Hamiltonian
H
0
kk
=
E
g
+
2
k
2
2m
δ
kk
− V
k−k
, (13.20)
and
∆H
kk
=2δ
kk
d
cv
E
p
p
∗
k
+2|p
k
|
2
V
k−k
− 2δ
kk
k
V
k−k
|p
k
|
2
+2δ
kk
p
∗
k
k
V
k−k
p
k
− 2p
k
V
k−k
p
∗
k
. (13.21)
We now expand the polarization induced by the test field in terms of
the unperturbed exciton eigenfunctions, i.e., in terms of the eigenfunctions
of the Hamiltonian (13.20):
δp
+
k
=
λ
δp
+
λ
ψ
λ,k
. (13.22)
Inserting this expansion into Eq. (13.19), multiplying with ψ
∗
λ,k
from the
left, and summing over all k yields
λ
(ω
λ
−ω
t
−iδ)δ
λλ
+∆H
λλ
δp
+
λ
=
k
ψ
∗
λ,k
(1 − 2|p
k
|
2
) d
cv
E
t
. (13.23)
Here, we introduced the perturbation Hamiltonian
∆H
λλ
=Π
λλ
+∆
λλ
, (13.24)
where Π
λλ
is the anharmonic interaction between the exciton and the pump
field,
Π
λλ
=2E
p
k
ψ
∗
λ,k
d
cv
p
∗
k
ψ
λ
,k
, (13.25)
January 26, 2004 16:26 WSPC/Book Trim Size for 9in x 6in b ook2
242 Quantum Theory of the Optical and Electronic Properties of Semiconductors
and ∆
λλ
is the exciton–exciton interaction
∆
λλ
=2
kk
V
k−k
ψ
∗
λ,k
(p
∗
k
− p
∗
k
)(p
k
ψ
λ
,k
+ p
k
ψ
λ
,k
) . (13.26)
We can rewrite Eq. (13.23) as
δp
+
λ
=
k
ψ
∗
λ,k
(1 − 2|p
k
|
2
)d
cv
E
t
−
λ
=λ
∆H
λλ
δp
+
λ
¯ω
λ
− ω
t
− iδ
, (13.27)
where ¯ω
λ
is the renormalized exciton frequency
¯ω
λ
= ω
λ
+∆H
λλ
/ . (13.28)
Eq. (13.27) can be solved iteratively with
δp
+(1)
λ
=
k
ψ
∗
λ,k
(1 − 2|p
k
|
2
)d
cv
E
p
¯ω
λ
− ω
t
− iδ
. (13.29)
Note, that in this procedure even the first-order result contains the shifted
exciton energies ω
λ
i.e., the Stark shift as well as the phase-space filling.
In the next order, one finds
δp
+(2)
λ
= δp
+(1)
λ
−
λ
=λ
∆H
λλ
δp
+(1)
λ
¯ω
λ
− ω
t
− iδ
. (13.30)
The linear optical susceptibility of the test beam is finally obtained as
χ
t
(ω
t
)=2
λ
d
∗
λ
δp
+
λ
E
t
, (13.31)
where
d
λ
=
k
d
cv
ψ
∗
λ,k
. (13.32)
The resulting susceptibility has the form (see problem 13.4)
χ
t
(ω
t
)=
2
λ
¯
f
λ
¯ω
λ
− ω
t
− iδ
, (13.33)
where
¯
f
λ
is the renormalized exciton oscillator strength:
¯
f
λ
= |d
λ
|
2
− 2d
∗
λ
k
ψ
∗
λ,k
|p
k
|
2
d
cv
+
λ
=λ
d
∗
λ
∆H
λλ
d
λ
+(λ λ
)
(ω
λ
− ω
λ
)
. (13.34)

January 26, 2004 16:26 WSPC/Book Trim Size for 9in x 6in b ook2
Excitonic Optical Stark Effect 243
Note, that the result (13.33) is put into the usual form of the exciton suscep-
tibility, but it contains renormalized exciton energies ¯ω
λ
and renormalized
oscillator strengths
¯
f
λ
. In this low-intensity regime, the quasi-stationary
optical Stark effect can be described completely in terms of shifts of the ex-
citon levels and in terms of changes of the exciton oscillator strengths. The
first correction term of the oscillator strength in Eq. (13.34) describes the
reduction due to phase-space filling, while the terms due to the perturba-
tion ∆H describe the corrections caused by the anharmonic exciton–photon
and the exciton–exciton interaction.
In the linear approximation in the pump field, the polarization p
k
can
be written in terms of an exciton Green’s function
p
k
(ω
p
)=−d
cv
E
p
G
r
(k, ω
p
) , (13.35)
with
G
r
(k, ω
p
)=−
λ
ψ
∗
λ,k
ψ
λ
(r =0)
(ω
λ
− ω
p
− iδ)
. (13.36)
For small detuning ω
p
− ω
1s
<< E
0
, the Green’s function simplifies to
G
r
(k, ω
p
)=−
ψ
∗
1s,k
ψ
1s
(r =0)
(ω
1s
− ω
p
− iδ)
, (13.37)
so that
Π
λλ
= ψ
∗
1s
(r =0)
k
ψ
1s,k
|ψ
λ,k
|
2
2|d E
p
|
2
(ω
1s
− ω
p
)
. (13.38)
The Stark shift due to the anharmonic exciton–photon interaction is equal
to the usual two-level Stark shift (2|d E
p
|
2
)/(ω
1s
− ω
p
) times an enhance-
ment factor due to the electron–hole correlation
ρ
λ
= ψ
∗
1s
(r =0)
k
ψ
1s,k
|ψ
λ,k
|
2
. (13.39)
For the band edge, we find with |ψ
λ=∞,k
|
2
= δ
k,0
ρ
∞
= ψ
∗
1s
(r =0)ψ
1s,k=0
. (13.40)
Using the two- and three-dimenisonal exciton wave functions (see Chap. 10)
January 26, 2004 16:26 WSPC/Book Trim Size for 9in x 6in b ook2
244 Quantum Theory of the Optical and Electronic Properties of Semiconductors
ψ
1s,k
=
√
2πa
0
1+(ka
0
/2)
2
3/2
ψ
1s,k
=
8
πa
3
0
1+(ka
0
)
2
2
,
we find (see problem 13.4)
ρ
1s
=
16/7
7/2
; ρ
∞
=
4
8
for
2D
3D
. (13.41)
For small detuning, we obtain the surprising result that the contribution of
the anharmonic exciton–photon interaction to the Stark shifts is larger for
the continuum states than for the exciton.
Similarly, the polarization–polarization interaction ∆
λλ
can be written for
small detuning as
8
7
6
5
4
3
2
1
0
-20
-18
-16 -14
-12 -10
-8 -6
-4
-2
0
D
edE[2d /| |]
CV p
22
DE
g
DE
x
DE
g
xp
DE
x
xp
Normalized Detuning
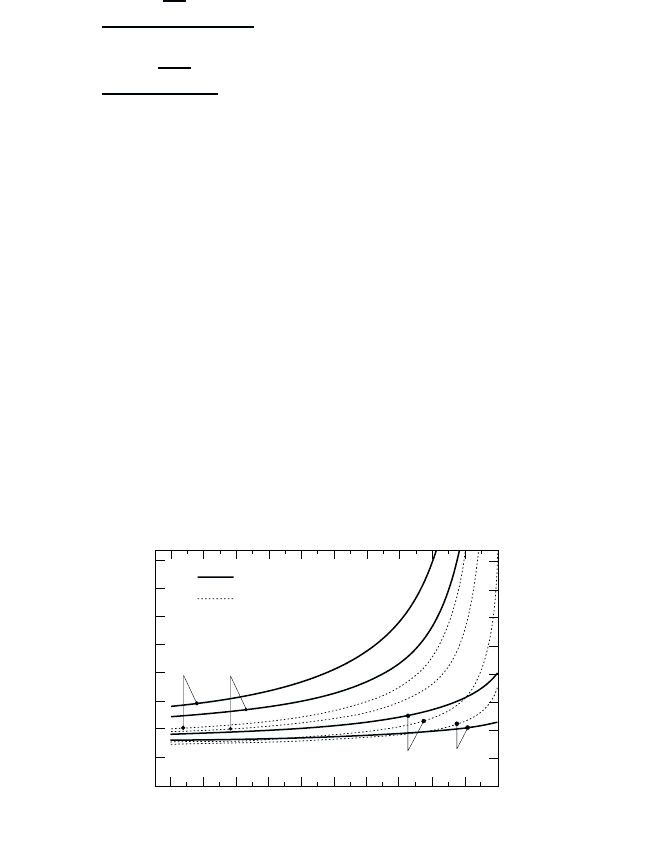
Fig. 13.4 Calculated shifts of the exciton ∆E
x
and of the band gap ∆E
g
versus normal-
ized detuning (ω
p
− E
1s
)/E
0
; as well as shifts due to the anharmonic exciton–photon
interaction alone, ∆E
xp
x
and ∆E
xp
g
respectively.

January 26, 2004 16:26 WSPC/Book Trim Size for 9in x 6in b ook2
Excitonic Optical Stark Effect 245
∆
λλ
=2|ψ
∗
1s
(r =0)dE
p
|
2
×
kk
V
k−k
ψ
∗
λ,k
(ψ
∗
1s,k
− ψ
∗
1s,k
)(ψ
1s,k
ψ
λ,k
− ψ
1s,k
ψ
λ,k
)
2
(ω
1s
− ω
p
)
2
= ν
λ
2|dE
p
|
2
(ω
1s
− ω
p
)
. (13.42)
The enhancement factor ν
λ
diverges as 1/(ω
1s
− ω
p
) for ω
p
→ ω
1s
. Again,
the integrals can be evaluated analytically and yield
ν
1s
=
E
0
(ω
1s
− ω
p
)
a
1s
, (13.43)
where
a
1s
=
64(1 − 315π
2
/2
12
)
26/3
15.4
8.66
for
2D
3D
, (13.44)
and
ν
∞
=
E
0
(ω
1s
− ω
p
)
a
∞
, (13.45)
where
a
∞
=
64(1 − 3π/16)
24
26.3
24
for
2D
3D
. (13.46)
Again, we see that these contributions to the Stark shifts are larger for the
continuum states than for the exciton ground state. For general values of
the detuning, the shifts have to be evaluated numerically. Fig. 13.4 shows
the resulting shifts of the exciton and the continuum states for varying de-
tuning. For all values of the detuning, the blueshift of the continuum states
is larger than that of the exciton ground state, i.e., the exciton binding
energy increases.
Now, we are in a position to understand the numerical results for the
quasi-stationary Stark effect shown in Fig. 13.3. The phase-space filling due
to the action of the pump beam, which would result in a reduction of the
oscillator strength of the exciton, is overcompensated by the anharmonic
exciton–photon and exciton–exciton interaction, which increase the binding
energy and thus the oscillator strength. These conclusions can indeed be
verified by evaluating the oscillator strength (13.34) explicitly.

January 26, 2004 16:26 WSPC/Book Trim Size for 9in x 6in b ook2
246 Quantum Theory of the Optical and Electronic Properties of Semiconductors
13.2 Dynamic Results
In our investigation of dynamical aspects of the optical Stark effect, we
again start from the coherent semiconductor Bloch equations, Eqs. (13.6)
and (13.7). We write the total field E as sum of pump E
p
and test field E
t
E(r,t)=E
p
(r,t)+E
t
(r,t)
= E
p
(t)e
−i(k
p
·r+Ωt)
+ E
t
(t)e
−i(k
t
·r+Ωt)
(13.47)
with k
p
= k
t
.
In order to obtain analytical results, we ignore the nonlinear terms, i.e.,
the terms involving products of polarizations and densities, i.e., we treat
only the linear coherent part
i
∂
∂t
− (
e,k
+
h,k
)
P
k
=(2n
k
− 1)d
cv
E(t) −
q=k
V
|k−q|
P
q
, (13.48)
∂
∂t
n
k
= i
d
cv
E(t)P
∗
k
− c.c.
, (13.49)
where we again assumed
n
h,k
= n
e,k
= n
k
. (13.50)
As initial conditions, we assume an unexcited system,
n
k
= P
cv,k
=0 .
As in Eqs. (10.31) - (10.35), we now transform the equations to real space:
i
∂
∂t
P (r)=H
eh
P (r)+d
cv
E(t)
2n(r) − δ(r)
(13.51)
and
∂
∂t
n(r)=i
d
cv
E(t)P
∗
(−r) − c.c.
, (13.52)
Here,
H
eh
= E
g
−
2
∇
2
2m
r
− V (r) (13.53)

January 26, 2004 16:26 WSPC/Book Trim Size for 9in x 6in b ook2
Excitonic Optical Stark Effect 247
is the Wannier Hamiltonian, compare Eq. (10.35). Note, that under the
present conditions the equations yield local charge neutrality,
n
e
(r)=n
h
(−r) ≡ n(r) .
Now, we multiply Eqs. (13.51) and (13.52) by ψ
λ
(r),whereψ
λ
(r) is the
eigenfunction of the Wannier equation (10.35). Then we integrate over r to
obtain
i
∂
∂t
P
λ
=
λ
P
λ
+ d
cv
E(t)
2n
λ
− ψ
λ
(r =0)
, (13.54)
and
∂
∂t
n
λ
= id
cv
E(t)P
∗
λ
− id
∗
cv
E(t)P
λ
, (13.55)
whereweusedthenotation
d
3
rψ
λ
(r)P (r)=P
λ
,
d
3
rψ
λ
(r)n(r)=n
λ
. (13.56)
The set of Eqs. (13.54) – (13.55) is closed for each λ. The source term in
Eq. (13.54) is proportional to the electron–hole–pair wave function in the
origin and therefore only the s-functions contribute. Hence, ψ
λ
(r) is a real
function that depends only on |r|.
Introducing now
P
λ
= ψ
λ
(r =0)P
λ
and n
λ
= ψ
λ
(r =0)N
λ
, (13.57)
we obtain the simplified equations of motion
∂
∂t
P
λ
= −(i
λ
+ γ)P
λ
−
id
cv
E(t)(2N
λ
− 1)
∂
∂t
N
λ
= −Γn
λ
+ i
d
cv
E(t)P
∗
λ
− i
d
∗
cv
E
∗
(t)P
λ
, (13.58)
where we added the appropriate phenomenological damping terms. We use
the total field in the form of Eq. (13.47). In order to eliminate the optical
frequencies, we introduce the notation
P
λ
≡ e
−iΩt
p
λ
and w
λ
≡ (1 − 2N
λ
) . (13.59)

January 26, 2004 16:26 WSPC/Book Trim Size for 9in x 6in b ook2
248 Quantum Theory of the Optical and Electronic Properties of Semiconductors
Inserting these definitions into Eqs. (13.58) yields
∂
∂t
p
λ
=[i(
λ
− Ω) + γ]p
λ
+ i
d
cv
E
p
(t) e
−ik
p
·r
+ E
t
(t) e
−ik
t
·r
w
λ
(13.60)
and
∂
∂t
w
λ
= −Γ(w
λ
− 1) − i
2d
cv
E
p
(t) e
−ik
p
·r
+ E
t
(t) e
−ik
t
·r
p
∗
λ
+ i
2d
∗
cv
E
∗
p
(t) e
ik
p
·r
+ E
∗
t
(t)e
ik
t
·r
p
λ
. (13.61)
In order to keep the theory as simple as possible, we assume that E
t
(t)
is short on all the relevant time scales, so we can approximate
E
t
(t)=E
t
δ(t − t
t
) . (13.62)
This corresponds to a broad frequency spectrum. The experiment measures
only that part of the signal which propagates in probe direction. Therefore,
we are interested only in that component of the solution for p
λ
which has
the spatial factor
∝ e
ik
t
·r
. (13.63)
Since we consider the case of an arbitrarily weak probe, we include only
terms which are linear in E
t
. To obtain analytic results, we ignore all terms
which are higher than second order in E
p
(t).
Clearly, for t<t
t
, we have no signal in the direction of the probe. The
only contribution is
p
λ
(t<t
t
)=i
d
cv
e
−ik
p
·r
t
−∞
dt
e
−
i(
λ
−Ω)+γ
(t−t
)
E
p
(t
)w
λ
(t
) .(13.64)
For that period of time during which the probe is incident on the sample,
we can solve Eq. (13.61) as
