Haug H., Koch S. Quantum theory of the optical and electronic properties of semiconductors
Подождите немного. Документ загружается.

January 26, 2004 16:26 WSPC/Book Trim Size for 9in x 6in b ook2
Semiconductor Bloch Equations 229
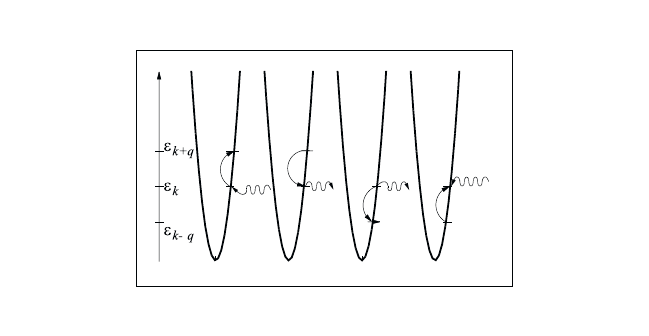
Fig. 12.1 Sketch of the four electron–phonon scattering processes. The solid lines sym-
bolize the electrons scattering from their initial to final states and the curled lines rep-
resent the phonon absorption or emission, respectively.
terms, emission and absorption is interchanged and the phonon momentum
q is reversed. These rates stem from the + functions. As a consequence
of the Markov approximation, the Boltzmann scattering rate depends only
on the distributions at time t and not on the values of the distributions
at earlier times. The Boltzmann scattering rates drive the system toward
thermal equilibrium, which is characterized by a maximum of the entropy.
In our case, the electrons will relax to thermal distributions with the lattice
temperature.
If one drops the assumption that only diagonal elements of the density
matrix exist, one gets for the scattering rate of the density n
i
(k) extra
terms arising from the population factors in the equations for F
−
ii,k,q
:
ig
q
N
q
ρ
i,j=i
(k)ρ
j=i,i
(k + q)−(N
q
+1)ρ
ij=i
(k + q)ρ
j=i,i
(k)
. (12.51)
These terms contain products of the interband polarization components,
showing that there is also scattering into and out of the coherently ex-
cited interband polarization. For shortness, these terms are often called P
2
terms. Before we discuss the influence of the other mean-field terms in the
equation for the phonon-assisted density matrix, we first analyze the basic
mechanisms of dephasing.

January 26, 2004 16:26 WSPC/Book Trim Size for 9in x 6in b ook2
230 Quantum Theory of the Optical and Electronic Properties of Semiconductors
12.3.2 Dephasing of the Interband Polarization
In order to analyze how the intraband phonon scattering destroys the co-
herent interband polarization, we now consider the off-diagonal elements
of the phonon-assisted density matrix equation (12.38), e.g., with i = c
and j = v again without the optical Stark effect terms and without the
Coulomb exchange terms:
∂F
−
cv,k,q
∂t
= i
&
v,k+q
−
c,k
− ω
0
+ iγ
cv,k,q
'
F
−
cv,k,q
+ ig
q
(
−N(ω
0
)ρ
cc
(k)ρ
cv
(k + q)+N(ω
0
)ρ
cv
(k)
1 − ρ
vv
(k + q)
+
N(ω
0
)+1
ρ
cc
(k+q)ρ
cv
(k)−
N(ω
0
)+1
ρ
cv
(k+q)
1−ρ
vv
(k)
)
.
(12.52)
Next, we note that the optically induced off-diagonal matrix elements are
rapidly oscillating functions. In order to insulate the slowly varying parts,
we split off the oscillations with the carrier frequency ω of the exciting light
field:
ρ
cv
(k,t)=e
−iωt
p
cv
(k,t) . (12.53)
A formal integration yields
F
−
cv,k,q
(t)=ig
q
e
−iωt
t
−∞
dt
e
i
&
v,k+q
−
c,k
+ω−ω
0
+iγ
cv,k,q
'
(t−t
)
×
(
−N(ω
0
)ρ
cc
(k,t
)p
cv
(k + q,t
)+N(ω
0
)p
cv
(k,t
)
1 − ρ
vv
(k + q,t
)
+
N(ω
0
)+1
ρ
cc
(k + q,t
)p
cv
(k,t
)
−
N(ω
0
)+1
p
cv
(k + q,t
)
1 − ρ
vv
(k,t
)
)
. (12.54)
This result shows that, due to the action of the light field in the off-diagonal
matrix elements, an electron state c, k is mixed with a valence band state
v, k, which in turn is scattered via phonon interaction into the state v, k+q.
In the long-time limit, this second-order process, which constitutes the
basic dephasing mechanism, is possible under energy conservation because
c,k
− ω
v,k
.
Inserting all phonon-assisted density matrices into the scattering rate
of the off-diagonal density matrix element, we obtain

January 26, 2004 16:26 WSPC/Book Trim Size for 9in x 6in b ook2
Semiconductor Bloch Equations 231
∂ρ
cv
(k,t)
∂t
scatt
=
−
q,σ
σg
2
q
e
−iωt
t
−∞
dt
e
i
&
v,k+q
−
c,k
+ω−σω
0
+iγ
cv,k,q
'
(t−t
)
×
(
N(σω
0
)
p
cv
(k,t
)n
h
(k + σq,t
) − p
cv
(k + σq,t
)n
e
(k,t
)
+
N(σω
0
)+1
p
cv
(k,t
)n
e
(k + σq,t
) − p
cv
(k + σq,t
)n
h
(k,t
)
)
−
(
k → k + σq
)
. (12.55)
The integral has a real part which describes the dephasing and an imaginary
part which describes the self-energy corrections due to the coupling to LO
phonons. These self-energies are called the polaron shifts. In the long-
time limit, we can again make the Markov approximation by pulling the
distribution functions out of the integral taking their values at the upper
time t. The integral over the remaining exponential yields a complex energy
denominator which can be decomposed into its real and imaginary part
using Dirac’s identity as explicitly shown above.
12.3.3 Full Mean-Field Evolution of the Phonon-Assisted
Density Matrices
Let us return to the equation (12.39) for the phonon-assisted density matrix,
which contains the full mean-field time development under the coherent
light field and the Coulomb Hartree–Fock terms. These terms introduce
into the scattering integrals the particle spectra renormalized by the op-
tical Stark effect and by the Coulomb exchange process. These spectral
renormalizations are time-dependent, i.e., they give the information which
particle spectra are realized at a given time. In order to include these
effects, we write (12.38) in the form
∂F
−
ij,k,q
∂t
=
∂F
−
ij,k,q
∂t
mf
+ R
ij,k,q
, (12.56)
where
R
ij,k,q
=
i
[H
e−LO
,a
†
j,k+q
a
i,k
b
q
] (12.57)

January 26, 2004 16:26 WSPC/Book Trim Size for 9in x 6in b ook2
232 Quantum Theory of the Optical and Electronic Properties of Semiconductors
is the inhomogeneous scattering term. The mean-field terms are defined in
Eq. (12.39). The solution of the inhomogeneous equation can be written as
F
−
ij,k,q
(t)=
l
t
−∞
dt
T
−
il
(t, t
)R
lj,k,q
(t
) . (12.58)
Here, T
−
il
(t, t
) is the time evolution matrix which develops according to the
mean-field Hamiltonian
∂T
−
ij,k,q
∂t
=
∂T
−
ij,k,q
∂t
mf
=
i
l
$
T
−
il,k,q
H
lj,k+q
−H
il,k
T
−
lj,k,q
%
−
&
iω
0
+γ
ij,k,q
'
T
−
ij,k,q
,
(12.59)
from the initial value T
ij,k,q
(t, t)=δ
ij
. The validity of the ansatz (12.58)
can be checked by direct insertion into (12.38). Note, that the time evolu-
tion matrix reduces simply to the free-particle exponential time evolution
T
ij,k,q
(t, t
) → e
i
&
j,k+q
−
i,k
−ω
0
+iγ
ij,k,q
'
(t−t
)
, (12.60)
if only the free-particle terms are considered. In the full solution for the
scattering term, the exponentials have simply to be replaced by the time
evolution operator T (t, t
).
So far the damping constants γ
ij,k,q
have been considered as infinites-
imal quantities. A detailed numerical inspection of the equations shows,
however, that, particularly for larger coupling constants, one needs finite
damping constants in order to obtain numerically stable solutions. It turns
out, that a self-consistent approach in which the damping constants are
also evaluated for the electron–LO phonon interaction yields the required
stability.
REFERENCES
For further reading on the material presented in this chapter see:
N. Peyghambarian, S.W. Koch, and A. Mysyrowicz, Introduction to Semi-
conductor Optics, Prentice Hall, Englewood Cliffs (1993)
H. Haug and S. Schmitt–Rink, Progr. Quantum Electron. 9, 3 (1984)
January 26, 2004 16:26 WSPC/Book Trim Size for 9in x 6in b ook2
Semiconductor Bloch Equations 233
H. Haug ed., Optical Nonlinearities and Instabilities in Semiconductors,
Academic Press, New York (1988)
A.StahlandI.Balslev,Electrodynamics of the Semiconductor Band Edge,
Springer Tracts in Modern Physics 110, Springer, Berlin (1987)
R. Zimmermann, Many-Particle Theory of Highly Excited Semiconductors,
Teubner, Leipzig (1988)
H. Haug and A.P. Jauho, Quantum Kinetics for Transport and Optics of
Semiconductors, Springer, Berlin (1996)
S. Mukamel, Principles of Nonlinear Optical Spectroscopy,OxfordUniver-
sity Press, Oxford (1995)
T. Kuhn, Density matrix theory of coherent ultrafast dynamics,inTheory
of Transport Properties of Semiconductor Nanostructures, ed. E. Schöll,
Chapmann and Hill, London (1998), pp. 173
W. Schäfer and M. Wegener, Semiconductor Optics and Transport Phe-
nomena Springer, Berlin (2002)
PROBLEMS
Problem 12.1: Derive the electron–hole Hamiltonian, Eq. (12.6).
Problem 12.2: Derive the multi-subband Coulomb interaction potential
(12.26). Hint: Use the envelope wave functions discussed in Sec. 5.2.2 and
perform the two-dimensional Fourier transform of Sec. 7.3 over the in-plane
coordinate r
.
Problem 12.3: Generalize the two-band many-body Hamiltonian,
Eq. (10.14), to the multi-band situation. Make the Hartree–Fock approxi-
mation to derive Eq. (12.25).
Problem 12.4: Show that the entropy density defined as
s(t)=−k
B
k
(
n
k
(t)ln
n
k
(t)
+(1− n
k
(t)) ln
1 − n
k
(t)
)
of an electron gas increases monotonously for the Boltzmann scattering rate
for electron–phonon interaction.
Problem 12.5: Derive the electron–LO phonon interaction constant g
q
(12.31) by considering the low- and high-frequency limit of the Coulomb
interaction in a polar medium. At low frequencies both the ion displacement

January 26, 2004 16:26 WSPC/Book Trim Size for 9in x 6in b ook2
234 Quantum Theory of the Optical and Electronic Properties of Semiconductors
and the orbital polarization are present, while at high frequencies the inertia
g
q
g
q
========== =
+
_______
V/
q0
e
V/
q
e
¥
D (q,0)
r
Fig. 12.2 Diagrams of the Coulomb and phonon-mediated interaction
of the ions is too large so that their oscillations cannot follow. Therefore,
V
q
0
=
V
q
∞
+ g
2
q
D
r
(q, ω 0) ,
with (ω =0)=
0
and (ω →∞)=
∞
, see Fig. 12.2. D
r
(q, ω) is the
retarded phonon Green’s function. The last term is the electron–electron
interaction caused by an exchange of a phonon. Calculate the free phonon
Green’s function from its definition in time with t
=0for t ≥ 0
D
r
(q, t)=−
i
[(b
†
q
(t)+b
−q
(t)), (b
q
+ b
†
−q
)] ,
and by using b
q
(t)=e
−iω
0
t
b
q
. Apply the Fourier transform into frequency
space and take the low-frequency limit.
January 26, 2004 16:26 WSPC/Book Trim Size for 9in x 6in b ook2
Chapter 13
Excitonic Optical Stark Effect
Very efficient experimental methods to study the optical properties of semi-
conductors are those that use two successive laser pulses, one to prepare
the system in a certain way and one to test it after a variable time delay.
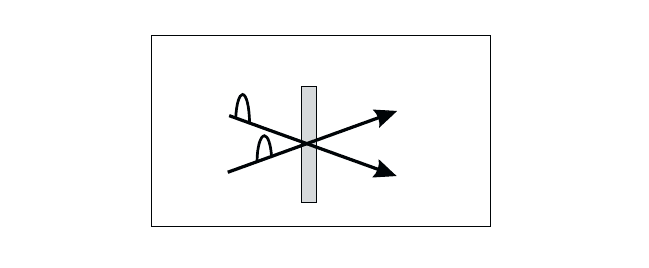
The simplest geometry of such an experiment is schematically shown in
Fig. 13.1.
Because the characteristic times for optical dephasing and relaxation of
band electrons in semiconductors are rather short, one has to use femto-
second laser pulses if one wants to study the quantum coherence and initial
relaxation stages of the excited states. Generally speaking, the dephasing
times become larger as the phase space of the excited electrons is reduced
by quantum confinement, particularly, if one eliminates all translational de-
grees of freedom as in quantum dots. It is also true that the dephasing times
are longer in the low-density regime where one excites primarily neutral
complexes such as excitons or biexcitons (two electron–hole–pair states),
E
probe
E
pump
k
p
k
t
Fig. 13.1 Geometry of a pump-probe experiment.
235
January 26, 2004 16:26 WSPC/Book Trim Size for 9in x 6in b ook2
236 Quantum Theory of the Optical and Electronic Properties of Semiconductors
particularly, in systems where their binding energies are large. Similarly,
if one excites spin-polarized states, one finds relatively slow spin dephas-
ing because spin–flip processes are relatively rare. In these cases, one can
use picosecond pulses instead of the femtosecond pulses mentioned before.
For the analysis of such time-resolved two-pulse experiments, the semicon-
ductor Bloch equations form the appropriate theoretical framework. The
coherent laser light field in these equations has to describe naturally both
pulses.
A very important example of a “coherent” semiconductor response is
the excitonic optical Stark effect, where a strong pump pulse excites the
material energetically below the exciton resonance and the probe pulse
monitors the transmission change at the exciton resonance. The optical
Stark effect in a two-level system has already been discussed in Chap. 2.
Here, the coherent light field mixes the wave functions of the two states
leading to the dressed states. Even though the Stark effect is well-known in
atomic systems, it was only observed in semiconductors in the mid 1980’s
because of the above mentioned short dephasing times.
Normalized Detuning
Normalized Detuning
Absorption
Differential Absorption
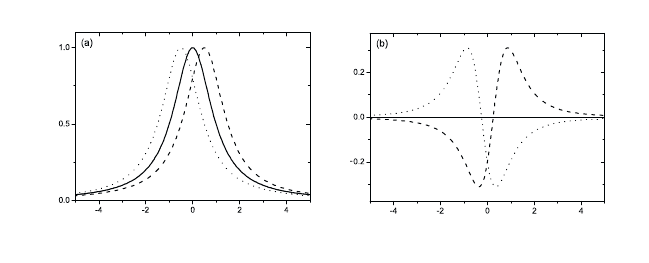
Fig. 13.2 (a) Redshift (shift to lower energies, dotted line) and blueshift (dashed line) of
an excitonic resonance α
0
(solid line) and (b) the resulting absorption change (differential
absorption) α − α
0
.
In our discussion of the optical Stark effect in semiconductors, we concen-
trate on the case of nonresonant excitation of the exciton, where it is a
good approximation to ignore absorption and generation of real carriers.
In this case, the optical Stark effect manifests itself as a light-induced shift
of the excitonic resonance. Depending on the selection rules of the optical
transitions this shift can be a blueshift, i.e. shift of the resonance to higher
energies, or a redshift (see Fig. 13.2).

January 26, 2004 16:26 WSPC/Book Trim Size for 9in x 6in b ook2
Excitonic Optical Stark Effect 237
We discuss different features of the excitonic optical Stark effect in three
steps. First, we present analytic results of a two-band model for a quasi-
stationary situation and then we discuss dynamic excitation conditions. In
the third step, we include the selection rules for the transitions and also
consider biexcitonic correlations, which allows us to discuss pump–probe
configurations for different polarizations of the pump and probe pulses.
13.1 Quasi-Stationary Results
In this section, we present the analysis of the quasi-stationary optical Stark
effect. This condition applies only when the amplitude variations of the
light field are so slow, that we can make an adiabatic approximation. For
femtosecond experiments, this procedure is generally not valid. Neverthe-
less, we start our discussion with that stationary case in order to understand
the similarities and differences of this coherent phenomenon in atomic and
semiconductor systems. Particularly, we analyze analytically the modifica-
tions due to the semiconductor many-body effects. Dynamical solutions for
pulsed excitation are then discussed in the following section.
As an introduction, we first reformulate the treatment of Chap. 2 of the
optical Stark shift of a two-level atom in terms of the Bloch equations for the
polarization and the population. In second quantization, the Hamiltonian
for the two-level system is
H =
j=1,2
j
a
†
j
a
j
−
d
21
E(t)a
†
2
a
1
+h.c.
(13.1)
with the coherent pump field E(t)=E
p
e
−iω
p
t
. Via the Heisenberg equation
for the operators, we get the following equations for the polarization P =
a
†
1
a
2
and the density in the upper state n = n
2
= a
†
2
a
2
=1− n
1
:
i
dP
dt
= P − (1 − 2n)
d
21
E
p
(13.2)
and
dn
dt
=
i
(d
21
E
p
P
∗
− h.c.) (13.3)
with =
2
−
1
. These two completely coherent equations (no damping
terms) have a conserved quantity (see problem 13.1)
K =(1− 2n)
2
+4|P |
2
. (13.4)
January 26, 2004 16:26 WSPC/Book Trim Size for 9in x 6in b ook2
238 Quantum Theory of the Optical and Electronic Properties of Semiconductors
With the initial condition n =0and P =0we have K =1,or
n =
1
2
(1 ±
1 − 4|P |
2
) . (13.5)
Eq. (13.5) shows that the density is completely determined by the polar-
ization. This is only true for a fully coherent process, or in the language of
quantum mechanics, for virtual excitations. These excitations of the atom
vanish if the field is switched off, whereas real excitations would stay in the
system and would decay on a much longer time scale determined by the
carrier lifetime. From Eqs. (13.2) - (13.5) one can again derive the results
of Chap. 2 (see problem 13.2).
Next, we turn to the coherent Bloch equations of the semiconductor
which have been derived in Chap. 12, see Eqs. (12.19). Here, we omit all
damping and collision terms, an approximation which is clearly not valid
for resonant excitation, where real absorption occurs. With n
k
= n
c,k
=
1 − n
v,k
, we can write Eqs. (12.19) as
i
dP
k
dt
= e
k
P
k
− (1 − 2n
k
)ω
R,k
(13.6)
dn
k
dt
= i(ω
R,k
P
∗
k
− ω
∗
R,k
P
k
) , (13.7)
where e
k
is the pair energy renormalized by the exchange energy
e
k
= (e
e,k
+ e
h,k
)=E
g
+
2
k
2
2m
− 2
k
V
k−k
n
k
(13.8)
and ω
R,k
is the effective Rabi frequency, Eq. (12.18).
Note, that there is a complete formal analogy between the two-level
atom equations (13.2) – (13.3) and the semiconductor equations (13.6) –
(13.7) for each k-state, except for the renormalizations of the pair energy
and of the Rabi frequency, which mix the k-states in a complicated way.
From this analogy, we get immediately the conservation law
n
k
=
1
2
(1 ±
1 − 4|P
k
|
2
) . (13.9)
If the fields are switched on adiabatically only the minus sign in Eq. (13.9)
can be realized and the relations 0 ≤ n
k
≤ 1/2 and 0 ≤|P
k
|
2
≤ 1/2 hold.
