Hassani S. Mathematical Physics: A Modern Introduction to Its Foundations
Подождите немного. Документ загружается.


0 _
Mathematical
Preliminaries
This introductory chapter gathers togethersome of the most basic tools andnotions
that are used throughout the book.
It
also introduces some common vocabulary
and notations used in modem mathematical physics literature. Readers familiar
with
suchconcepts as sets,
maps,
equivalence
relations,
and
metric
spaces
may
wish to skip this chapter.
0.1.
Sets
Modem mathematics starts with the basic (and undefinable) concept of set. We
think
of
a set as a structureless family, or collection, of objects. We speak, for
example, of the set of students in a college,
of
men in a city,
of
women working
concept
ofset for a corporation, of vectors in space,
of
points in a plane, or
of
events in the
elaborated
continuum
of
space-time. Each member a of a set A is called an element of that
sel. This relation is denoted by a E A (read "a is an element
of
A"
or "a belongs
to
A"),
and its negation by a ¢ A. Sometimes a is called a
point
of
the set A to
emphasize a geometric connotation.
A set is usually designated by enumeration
of
its elements between braces.
For example, {2,4, 6, 8}represents the set consisting
of
the first four even natural
numbers;
{O,
±I,
±2,
±3,
...
}is the set
of
all integers; {I, x, x
2
,
x
3,
...
} is the
set of all nonnegativepowers
of
x; and {I, i,
-1,
-i}
is the set of the four complex
fourth roots
of
unity.
In
many cases, a set is defined by a (mathematical) statement
that holds for all
ofits
elements. Such a
set
is generally denoted by {x IP
(x)}
and
read "the set of all
x's such that
P(x)
is true." The foregoing examples of sets can
be written alternatively as follows:
{n In is even and I < n < 9}

2
O.
MATHEMATICAL
PRELIMINARIES
{±n In is a natural number}
{y Iy =
x"
and n is a uatural uumber}
{z IZ4 = I and zis a complex uumber}
singleton
(proper)
subset
empty
set
union,
intersection,
complement
universal
set
Cartesian
product
ordered
pairs
In a frequently used shorthand uotation, the last two sets
can
be abbreviated as
[x"
In 2: aand n is an integer} and [z E
iC
IZ4 = I}. Similarly, the uuit circle
can be deuoted by {z
[z] = I}, the closed interval [a, b] as {xla ::; x ::; b}, the
open interval
(a, b) as {x Ia < x < b}, and the set of all nonnegative powers
of
x as
{x"}~o'
This last notation will be used frequeutly iu this book. A set with a
single element is called a singleton.
If
a E A whenever a E B, we say that B is a
subset
of
A and write B C A or
A:J
B.
If
Be
A and A c B, then A =
B.1f
Be
A and A
i'
B,
thenB
is called
a
proper
subset of A. The set defined by {ala
i'
a}is
called the
empty
set
and
is denoted by 0. Clearly, 0 contains no elements and is a subset
of
any arbitrary
set. The collection of all subsets (including 0) of a set
A is denoted by 2
A
•
The
reason for this notation is that the number of subsets
of
a set containingn elements
is 2" (Problem
a.I).1f
A and B are sets, their
union,
denoted by A U B, is the set
containingall elementsthat belongto
A or B or both. The intersection of the sets
.!\ and B, denoted by A n B, is the set containing all elements belonging to both
A and B.
If
{B.}.El
is a collection of sets,
1
we denote their union
by
U.B.
and
their intersection by
n.B
a-
In
any application of set theory there is an underlying
universal
set whose
subsets are the objects
of
study. This universal set is usually clear from the context.
For
exaunple, in the study
of
the properties of integers, the set of integers, denoted
by Z, is the universal set. The set
of
reals,
JR,
is the universal set in real analysis,
and the set of complex numbers,
iC,
is the universal set in complex analysis. With
a universal set X in mind, one can write X
~
A insteadof ~ A. The
complement
of
a set A is denoted by ~ A and defined as
~
A sa {a Ia
Ii!
A}.
The complement of B in A (or their difference) is
A
~
B
==
{ala E A and a
Ii!
B}.
From two given sets A and B, it is possible to form the
Cartesian
prodnct
of A
and B, denoted by A x B, which is the set
of
ordered
pairs
(a, b), where a E A
and b E B. This is expressed in set-theoretic notatiou as
A x B ={(a, b)la E A and b e B}.
1Here I is an index
set--or
a counting
set-with
its typical element denotedby ct. In most cases, I is the set
of
(nonnegative)
integers, but, in principle,
it can be any set, for example, the set
of
real numbers.

relation
and
equivalence
relation
0.1
SETS
3
We can generalize this to an arbitrary number
of
sets.
If
AI, A
z,
...
, An are sets,
then the Cartesian product of these sets is
Al x Az x
...
x An = {(ai, az,
...
,an)!ai E
Ad,
which is a set of ordered n-tuples.
If
Al = Az = ... = An = A, then we write
An instead of A x A
x···
x A, and
An = {(ai, az,
...
, an) Ia; E Aj.
The most familiar example of a Cartesian product occurs when A = R Then
JRz
is the set of pairs (XI,xz) with XI,xz E
JR.
This is simply the points in the
Euclidean plane. Similarly,
JR3
is the set
of
triplets (XI,xz, X3), or the points in
space, and
JRn
=
{(XI,
Xz,
...
,
Xn)!Xi
E
JRj
is the set
of
real n-tuples.
0.1.1 Equivalence Relations
There are many instances in which the elements
of
a set are naturally grouped
together. For example, all vector potentials that differ by the gradient of a scalar
function can be grouped together because they all give the same magnetic field.
Similarly, all quantum state functions
(of
unit "length") that differ by a multi-
plicative complex number of unit length
can
be grouped together because they all
represent the same physical state. The abstraction
of
these ideas is summarized in
the following definition.
0.1.1. Definition.
Let
A be a set. A relation on A is a comparison test between
ordered pairs
of
elements
of
A.
If
the pair (a, b) E A x A pass this test, we write
at>
b and read "a is related to
b"
An equivalence relation an A is a relation that
has the fallowing properties:
af>a
V'aEA,
a s-b
~
b s a
a.b
e A,
a
i-b.b»
c
==>-
a[>c
a.b;c
E A,
(reflexivity)
(symmetry)
(transivity)
When a t> b, we say that "a is equivalentto
b"
The set
[a]
= {b E
Alb
t> aj
of
all
equivalence
class elements that are equivalent to a is called the equivalence class
of
a.
The reader may verify the following property of equivalence relations.
0.1.2. Proposition.
If
» is an equivalence relation an A and a, b E A, then either
[a]
n
[b]
= 0 or
[a]
=
[bl
representative
ofan
equivalence
class
Therefore,
a' E
[a]
implies that
[a']
=
[a].
In
other words, any element
of
an equivalence class
can
be chosen to be a
representative
of
that class. Because
of
the symmetry
of
equivalence relations, sometimes we denote them by
c-o.

4
O.
MATHEMATICAL
PRELIMINARIES
0.1.3.
Example.
LetA bethe setofhumanbeings.Leta
»b
beinterpretedas"a is older
than b." Then clearly, I> is a relation but not an equivalence relation.
On
the other hand,
if
we interpret a
E>
b as "a and b have the same paternal grandfather," thenl> is an equivalence
relation, as the reader
may
check. The equivalence class
of
a is the set of all grandchildren
of
a's paternal
grandfather.
Let
V be the set of vector potentials. Write A l> A'
if
A -
A'
= Vf for some function
f. The reader may verify
that"
is an equivalence relation.and that
[A]
is the set of all
vectorpotentials giving rise to the
same
magnetic field.
Let the underlying set be Z x (Z -
{OJ).
Say"(a, b) is relatedto (c,
d)"
if ad = be.
Thenthis relation is an equivalence relation. Furthermore,
[(a,
b)]
can
be identified as the
ratio
a/b.
l1li
0.1.4. Definition.
Let
A be a set
and
{R
a}
a collection
of
subsets
of
A. Wesay that
partition
ofa set {R
a}
is a partition
of
A, or {R
a}
partitions A, ifthe R
a'
s are disjoint, i.e., have
noelementin
common,
and
Uo;B
a
= A.
Now consider the collection
{[a]
Ia E A}
of
all equivalence classes
of
A.
quotient
set These classes are disjoint, aod evidently their union covers all
of
A. Therefore,
the collection
of
equivalence classes
of
A is a partition
of
A. This collection is
denotedby
A/1><1
aod is calledthe
quotient
set
of
Aunderthe equivalencerelation
1><1.
0.1.5.
Example.
Letthe underlyingsetbe
lll.3.
Definean equivalence relationon
lll.3
by
saying that PI E lR
3
and P2 E
}R3
are equivalent
if
theylie on the
same
line passingthrough
the origin. Then
]R3
I l><l is the set
of
all lines in space passing through the origin.
If
we
choose the unit vectorwith positive third coordinate along a given line as the representative
of
thatline, then]R3I l><lcan be identifiedwith the upper unit hemisphere.e
]R3
I l><lis called
projective
space
the
projective
space
associated with]R3.
On
the set
IE
of
integers define a relation by writing m
e-
n for m, n E
IE
if
m - n is
divisible by
k,where
k is a fixed integer. Then e-is not only a relation, but an equivalence
relation.
In this case, we have
Z/"
= {[O],
[1],
...
,
[k
- I]},
as the readeris urged to verify.
For
the equivalence relation defined on
IE
x
IE
of
Example 0.1.3, the set
IE
x
lEI
l><l
can
be identified with
lQ,
the set
of
rational numbers.
II
0.2 Maps
map,
domain,
codomain,
image
To communicate between sets, one introduces the concept
of
a map. A
map
f
from a set X to a set Y, denoted by f : X
->
Y
or
X
~
Y, is a correspondence
between elements
of
X aod those
of
Y in which all the elements
of
X participate,
2Purthermore, we need to identify any two points on the edge of the hemisphere which lie on the same diameter.

0.2 MAPS 5
Figure 1 The map f maps all of the set X onto a subset of Y. The shadedareain Y is
f(K),
therangeof
f.
and each element
of
X corresponds to only one element
of
Y (see Figure 1).
If
y E Y is the element that corresponds to x E X
via
the map
f,
we write
y =
f(x)
or x f-->
f(x)
or
and call
f (x) the
image
of
x onder
f.
Thus, by the definition
of
map, x E X can
have only one image.
The
set X is called the
domain,
and Y the
codomain
or
the
target
space. Two maps f : X
-->
Y and g : X --> Y are said to be equal if
function
f(x)
=
g(x)
for all x E X.
0.2.1. Box. A map whose codomain is the set
of
real numbers
IR
or the set
of
complex numbers
iC
is commonly called afunction.
A special map that applies to all sets A is idA : A --> A, called the
identity
identity
map
map
of
A, and defined by
VaEA.
graph
ofa
map
The
graph
rf
of
a map f :A --> B is a subset
of
Ax
B defined by
rf = {(a,
f(a))
Ia E A} C A x B.
This general definition reduces to the ordinary graphs encountered in algebra and
calculus where
A = B =
IR
and A x B is the xy-plane.
If
A is a subset
of
X,
we call
f(A)
=
{f(x)lx
E A} the image
of
A. Similarly,
if
B C
f(X),
we call
preimage
f-
1(B)
= {x E
Xlf(x)
E B) the inverse image, or
preimage,
of
B. In words,
f-
1
(B) consists
of
all elements in X whose images are in B C
Y.1f
B consists
of
a single element b, then
r:'
(b) = {x E
Xlf(x)
= b) consists
of
all elements
of
X that are mapped to b. Note that it is possible for many points
of
X to have
the same image in
Y.
The
subset
f(X)
of
the codomain
of
a
map
f is called the
range
of
f (see Figure 1).
6
O.
MATHEMATICALPRELIMINARIES
Figure2 The
composition
oftwo
maps
is
another
map.
composition
of
two
maps
injection,
surjection,
and
bijection,
or1-1
correspondence
inverse
of
a
map
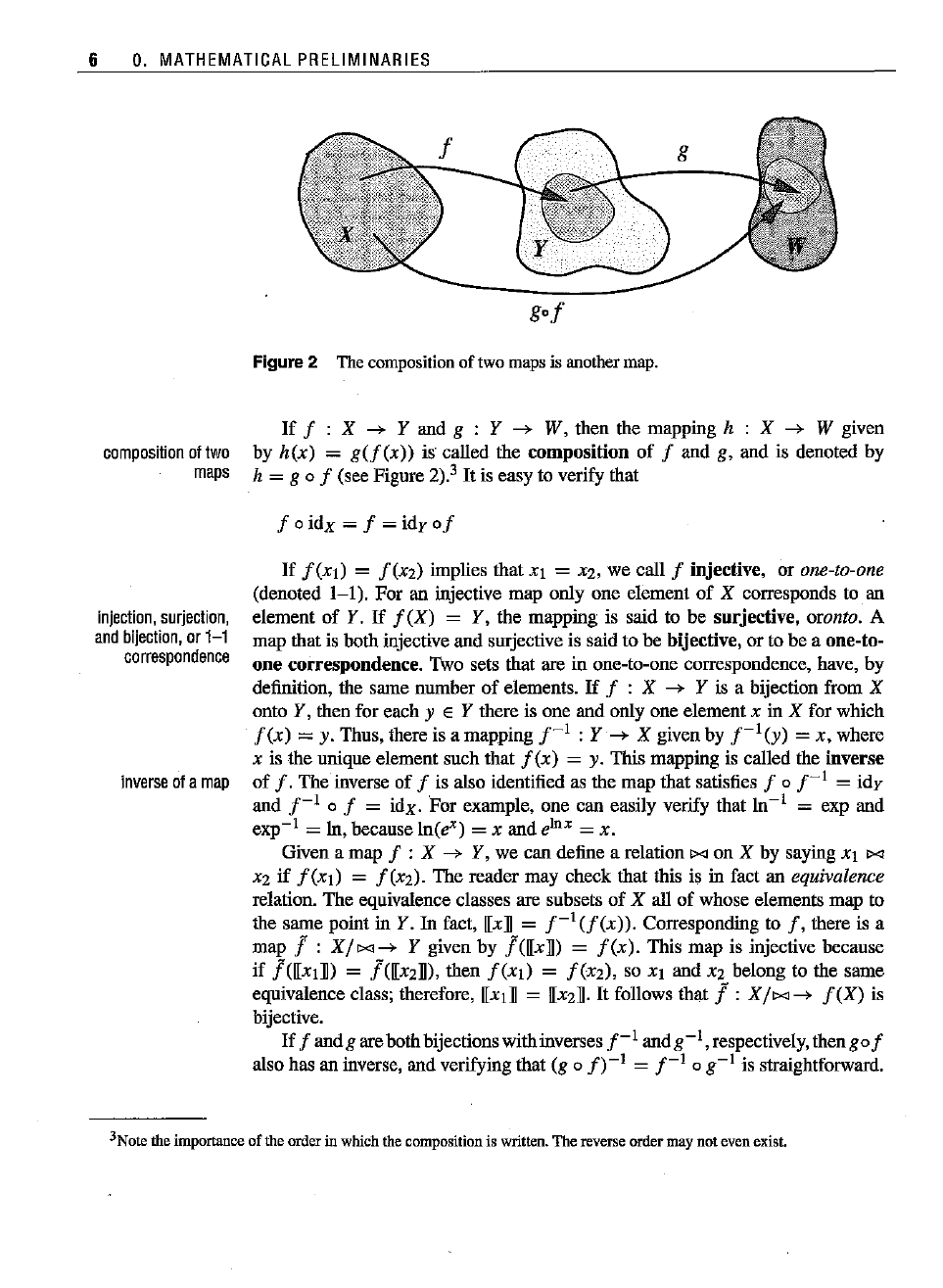
If
I : X
-->
Y and g : Y --> W, then the mapping h : X
-->
W given
by
h(x)
=
g(f(x))
is' called the composition of I and g, and is denoted by
h = g 0 I (see Figure 2).3
It
is easy to verify that
loidx=l=idyol
If
l(xI)
=
I(X2)
implies that XI = X2, we call I injective, or one-to-one
(denoted
I-I).
For an injective map only one element of X corresponds to an
element of
Y.
If
I(X)
= Y, the mapping is said to be surjective, oronto. A
map that is both injective and surjective is said to be bijective, or to be a one-to-
one correspondence. Two sets
that
arein one-to-one correspondence, have, by
definition, the same nnmber of elements.
If
I : X
-->
Y is a bijection from X
onto Y, then for each y E Y there is one and only one element X in X for which
I(x)
= y. Thus, there is a mapping
I-I
: Y --> X given by
I-I(y)
=
x,
where
X is the nniqne element such that
I(x)
= y. This mapping is called the inverse
of
I.
The inverse of I is also identified as the map that satisfies I 0
I-I
= idy
and
I-I
0 I = idx- For example, one can easily verify that ln
-I
= exp and
exp"! = ln, because In(e
X
)
= X and e
lnx
= x.
Given a map I : X --> Y, we can define a relation txl on X by saying XI txl
X2
if
l(xI)
=
I(X2).
The reader may check that this is in fact an equivalence
relation. The equivalence classes are subsets of X all of whose elements map to
the same point in Y. In fact,
[x]
=
1-1(f(X».
Corresponding to I, there is a
map!
:
X/txl-->
Y given by
!([x])
=
I(x).
This map is injective because
if
!([XI])
=
!([X2]),
then
l(xI)
=
I(X2),
so
XI
and X2 belong to the same
equivalence class; therefore, [XI] = [X2].
It
follows
that!
: X/txl-->
I(X)
is
bijective.
If
I andg arebothbijections withinverses
I-I
andg
-I,
respectively,thengoI
also has an inverse, and verifying that (g 0
f)-I
=
I-log-I
is straightforward.
3Notethe
importance
of the
order
in whichthecomposition is
written.
The
reverse
ordermaynotevenexist.

0.3
METRIC
SPACES
7
0.2.2.
Example.
As
an example
of
the preirnage
of
a set, consider the sine and cosine
functions.
Then
it
should
beclear
that
.
-10
{
JOO
SID = nn:
n=-oo'
cos-
1
0
=
{i
+mT:
J:-
oo
III
in{ectivity
and
surjectivity
depend
on
the
domain
and
codomain
unit
circle
binary
operation
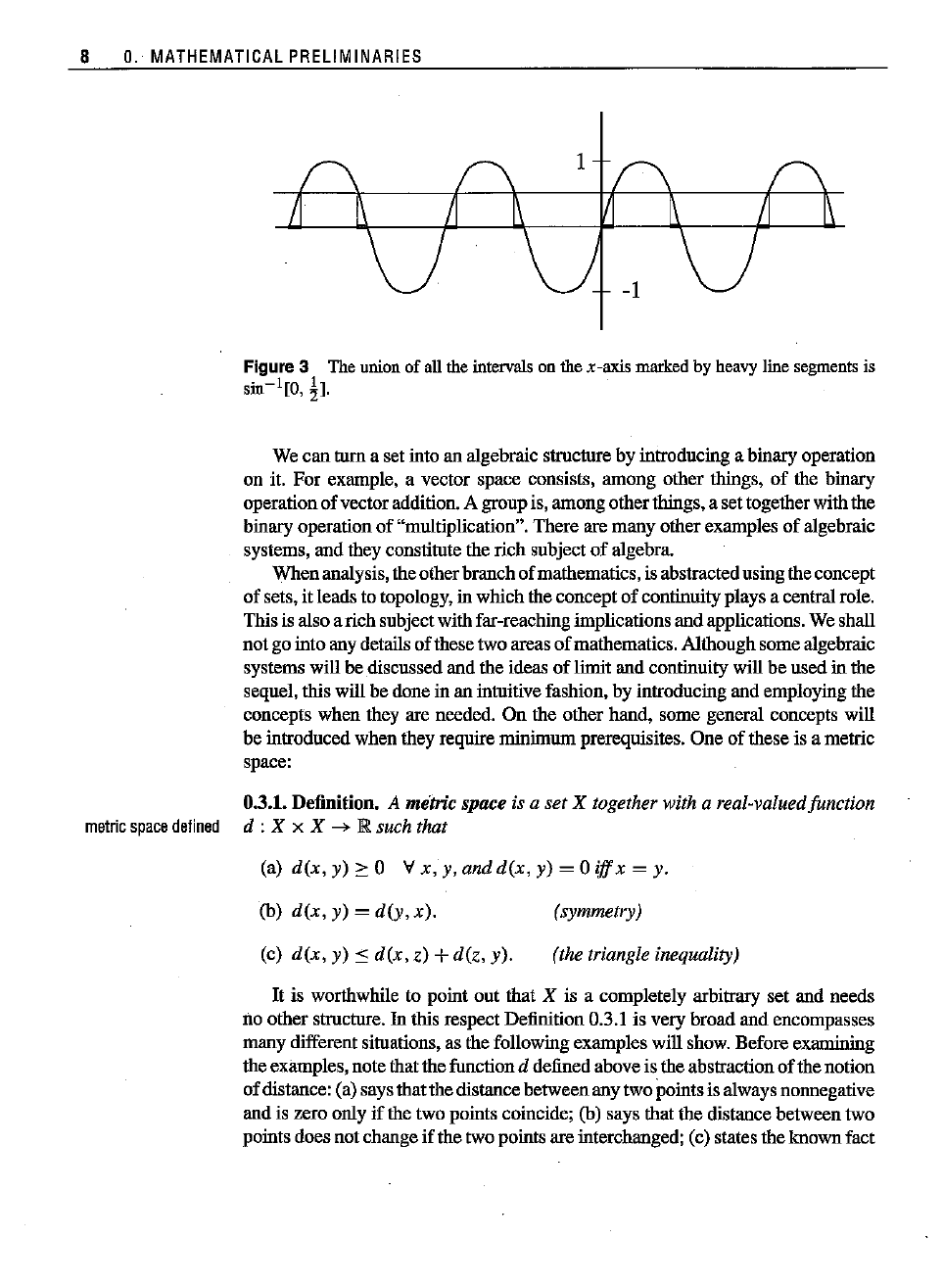
Similarly,
sin-
1[O,
!l
consists
of
all the intervals on the x-axis marked
by
heavy line
segments
in
Figure
3, i.e., allthepointswhosesineliesbetween0 and
~.
As examples of maps, we consider fonctions 1 :lR
-+
lR
stndied in calculus.
The Iwo fonctions
1 :
lR
-+ lR aud g : lR -+
(-I,
+
I)
given, respectively, by
1
(x)
= x
3
aud
g(x)
= taubx are bijective. The latter function, by the way,shows
that there are as mauy points in the whole real line as there are in the interval
(-I,
+1).
If
we denote the set of positive real numbers by lR+, then the function
1 : lR -+ lR+ given by
I(x)
= x
2
is surjective but not injective (both x aud
~x
map to x
2
).
The function g : lR+
-+
lRgiven by the same rule,
g(x)
= x
2
,
is injective but not surjective. On the other haud, h : lR+
-+
lR+ again given by
h(x)
= x
2
is bijective, but u : lR-+ lRgiven by the same rule is neither injective
nor surjective.
LetM
nxn
denotethe set
ofn
xn
real matrices. Definea functiondet :M
nxn
---+
lR
by det(A) = det A,where det Ais the determinaut
of
Afor A E J\1nxn. This fonc-
tion is clearly surjective (why?) but not injective. The set of all matrices whose
determinaut is 1 is
det-
I
(I). Such matrices occur frequently in physical applica-
tions.
Another example
of
interest is 1 :C -+ lRgiven by 1(z) = [z].This function
is also neither injective nor swjective. Here
1-
1
(1) is the unit circle, the circle
of radius
I in the complex plaue.
The domain of amap cau be a Cartesiauproductof a set, as in
1 :X x X -+ Y.
Two specific cases are worthy of mention. The first is when Y = R An example
of
this case is the dot product onvectors, Thus,
if
X is the set of vectors in space,
we cau define
I(a,
b) =
a·
b. The second case is when Y = X. Then 1 is
called a
binary operation on X, whereby au element in X is associated with two'
elements in X. For instance, let X
= Z, the set of all integers; then the fonction
I:
Z
xZ
-+ Zdefinedby
[tm,
n) = mn is the binary operationof multiplication
of
integers. Similarly, g : lR x lR
-+
lRgiven by
g(x,
y) = x +y is the binary
operation of addition
of
real numbers.
0.3 Metric Spaces
Although sets are at the root of modem mathematics, they are only of formal aud
abstract interest by themselves. To make sets useful, it is necessary to introduce
some structnres on them. There are two general procedures for the implementa-
tion
of
such structnres. These are the abstractions
of
the two major brauches
of
mathematics-algebra aud aualysis.
8
O.
MATHEMATICAL
PRELIMINARIES
Figure 3 Theunionof allthe
intervals
onthex-axis
marked
by heavyline
segments
is
.
-1[0
1]
sm
,~
.
We
can
turn
a set into an algebraic structure by introducing a binary operation
on it. For example, a vector space consists, among other things, of the binary
operationof vectoraddition. A groupis, among otherthings, a settogetherwith the
binary operation
of
"multiplication". There are many otherexamples
of
algebraic
systems, and they constitute the rich subject
of
algebra.
Whenanalysis, the otherbranchof mathematics, is abstractedusingthe concept
of sets, it leads to topology, in which the concept
of
continuity plays a central role.
This is also a rich subjectwith far-reaching implicationsand applications. We shall
not go into any details of thesetwo areas of mathematics. Although some algebraic
systems will be discussed and the ideas
of
limit and continuity will be used in the
sequel, this will be done in an intuitive fashion, by introducing and employing the
concepts when they are needed. On the other hand, some general concepts will
be introduced when they require minimum prerequisites. One of these is a metric
space:
0.3.1. Definition.
A metric space is a set X together with a real-valuedfunction
metric
space
defined
d:
X x X
~
lRsuch that
(a)
d(x,y)
2:0
VX,y,andd(x,y)=Oiffx=y.
(b)
d(x,
y) =
d(y,
x).
(c)
d(x,
y) :::
d(x,
z) +d(z, y).
(symmetry)
(the triangle inequality)
It is worthwhile to point
out
that X is a completely arbitrary set and needs
no other structure.
In this respect Definition 0.3.1 is very broad and encompasses
many different situations, as the following examples will show. Before exantining
the examples, note that the function
d definedabove is the abstraction
of
the notion
of distance: (a) says that the distancebetweenany two points is always nonnegative
and is zero ouly
if
the two points coincide; (b) says that the distance betweentwo
points does not change if the two points are interchanged; (c) states the knownfact

0.3
METRIC
SPACES
9
that the sum of the lengths
of
two sides of a triangle is always greaterthanor equal
to the length
of
the third side. Now consider these examples:
1. Let X =
iQI,
the set of rational numbers, and define
d(x,
y) = Ix -
yl.
2.
Let
X = R, and again define
d(x,
y) = Ix -
yl.
3.
Let
X consist of the points on the surface
of
a sphere. We can define two
distance functions on X.
Let
dt (P, Q) be the length
of
the chordjoining P
and Q on the sphere. We can also define another metric, dz(P, Q), as the
length of the arc of the great circle passing through points
P and Qon the
surface
of
the sphere.
It
is not hardto convince
oneself
that dl and
da
satisfy
all the properties
of
a metric function.
4.
Let
eO[a,b] denote the set
of
continuous real-valuedfunctions on the closed
interval
[a, b]. We can define
d(f,
g) =
J:
If(x)
- g(x)1
dx
for
f,
g E
eO(a, b).
5. Let
en(a,
b) denote the set
of
bounded continuons real-valned fnnctions on
the closed interval
[a, b]. We then define
d(f,
g) = max
lIf(x)
- g(x)IJ
xe[a,b]
for f, g E
eB(a,
b). This notation says: Take the absolute valne
of
the
differencein
f
andg
at all x in the interval [a, b] and then pickthe maximum
of
all these values.
The
metric
function
creates
a
natural
setting
in which
to
testthe"closeness"
of
points
in a
metric
space.
Oneoccasiononwhichtheideaof closenessbecomes
sequence
defined
essential is in the study
of
a seqnence. A sequence is a mapping s : N --* X from
the set
of
natural numbers N into the metric space X. Such a mapping associates
with a positive integer
n
apoints(n)
of the metric space X.
It
is customaryto write
Sn (or X
n
to match the symbol X) instead
of
s(n)
and to enumerate the values
of
the function by writing
{xnJ~I'
Knowledgeof the behaviorofa sequencefor large values of n is of fundamental
importance.
In
particular, it is important to know whether a sequence approaches
convergence
defined
a finitevalue as n increases.
0.3.2. Box. Suppose thatfor some x andforanypositiverealnumber e, there
exists a natural number N such that
dtx-;
x)
< e whenevern > N. Then we
say that the sequence
{xn}~l
converges to x and write
limn~oo
d(x
nl
x) =
Oar
d(x
no
x) --* 0 or simply X
n
--*
X.
It
may not be possible to test directly for the convergence
of
a given sequence
because this requires a knowledge of the limit point
x. However, it is possible to

10
O.
MATHEMATICAL
PRELIMINARIES
Figure 4 The distancebetween the elements of a Cauchy sequence gets
smaller
and
smaller.
Cauchy
sequence
complete
metric
space
do the next best
thing-to
see whether the poiots
of
the sequence get closer and
closer as
n gets larger and larger. A
Cauchy
sequence
is a sequence for which
limm.n-->oo
d(x
m,
x
n)
= 0, as shown in Figure 4. We can test directly whether
or not a sequence is Cauchy. However, the fact that a sequence is Cauchy does
not guarantee that it converges.
For
example,
let
the metric space be the set of
rational numbers
IQI
with the metric function
d(x,
y) = Ix -
YI,
and consider the
sequence
{xn}~l
where X
n
=
Lk~l
(-
li+
1
/
k.
It
is clear that X
n
is a rational
number for any
n. Also, to show that IX
m
-
X
n
I 4 0 is an exercise in calculus.
Thus, the sequence is Cauchy. However, it is probably known to the reader that
lim
n
--+
oo
X
n
= In2, whichis not a
rational
number.
A metricspace io which every Cauchysequenceconverges is calledacomplete
metric
space. Complete metric spaces
playa
crucial role in modern analysis. The
precediog example shows that
IQI
is not a complete metric space. However,
if
the
limit poiots of
all Cauchy sequences are added to
IQI,
the resulting space becomes
complete. This complete space is,
of
course, the real number systemR It tums out
that any iocomplete metric space
can
be "enlarged" to a complete metric space.
0.4 Cardinality
The process of counting is a one-to-one comparison
of
one set with another.
If
two
cardinalily
sets are io one-to-one correspondence, they are said to have the same
cardinality.
Two sets with the same cardinalityessentiallyhave the same "number"of elements.
The set
F
n
= {I, 2,
...
, n} is finite and has cardinalityn. Any set from which there
is a bijection onto
F
n
is said to be finite with n elements.
Although
some
steps
hadbeen
taken
before
himin the
direction
of a
definitive
theory
of
sets,thecreatorofthetheoryofsetsis considered to beGeorg Cantor (1845-1918), who
was bornin Russiaof Danish-Jewish
parentage
butmoved to
Germany
withhis
parents.
