Hancock G.J., Murray Th.M., Ellifritt D.S. Cold-Formed Steel Structures to the AISI Specification

Подождите немного. Документ загружается.

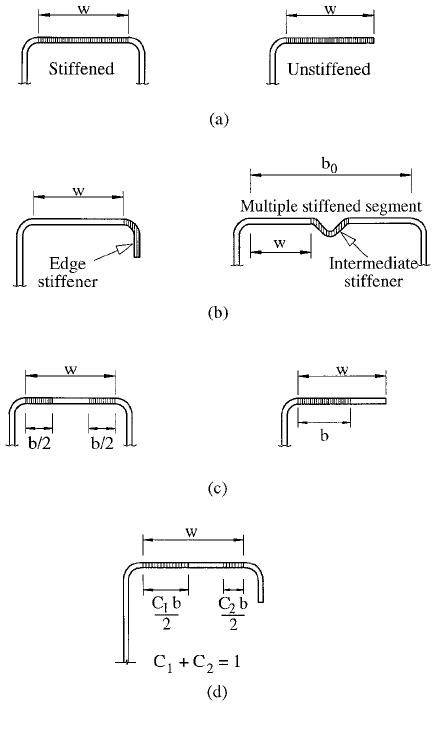
stiffener's adequacy was a clearly de®ned limiting moment

of inertia, dependent on the slendernessÐthat is, the

width-to-thickness ratioÐof the element being stiffened.

If stiffened elements were very slender, the real width

might have to be reduced to an effective width, as shown

in Figure 1.12c. The effective area thus computed for a

FIGURE 1.12 Compression elements: (a) compression elements;

(b) stiffeners; (c) effective widths; (d) effective width for a

partially stiffened element.

Chapter 1

complete section, when divided by the gross area, produced

an area reduction factor called Q

Effective area was not calculated for unstiffened

elements. The lower buckling stress on an unstiffened

element was calculated according to formulas which were

a function of the slenderness of the element. The resulting

stress, when divided by the design stress, usually 0:6F

produced a stress reduction factor, called Q

. The total

reduction on a section in compression was Q

 Q

In the 1986 edition of the speci®cation, a major shift in

philosophy was made. Now all compression elements are

treated with an effective width approach, as shown in

Figure 1.12c. There is one basic effective width equation

and the only difference that separates one element from

another is the plate buckling constant, k, which is

discussed in detail in Chapter 4. Even though the speci®ca-

tion still speaks of stiffened and unstiffened elements, most

elements are stiffened to some degree according to their

edge conditions and stress gradients, and one can begin to

think in terms of only one kind of element: a partially

stiffened element, as shown in Figure 1.12d. Q

and Q

are

no more.

Formerly, in a section such as a channel that has a

¯ange stiffened by a web on one side and a lip on the other,

the ¯ange was considered a stiffened element. Now, there is

a distinction between the ¯ange of a channel and the ¯ange

of a hat section which is attached to webs on both sides. The

channel ¯ange is now called an edge-stiffened element,

while the ¯ange of the hat is still called a stiffened element.

The edge stiffener usually produces effective widths distrib-

uted as shown in Figure 1.12d.

The web of either type of section, which has a portion

of its depth in compression, is also now treated with an

effective width approach, as are all elements with a stress

gradient. The only items that change are the plate buckling

coef®cient (k) and the distribution of the effective widths, as

discussed in Chapter 4.

Introduction

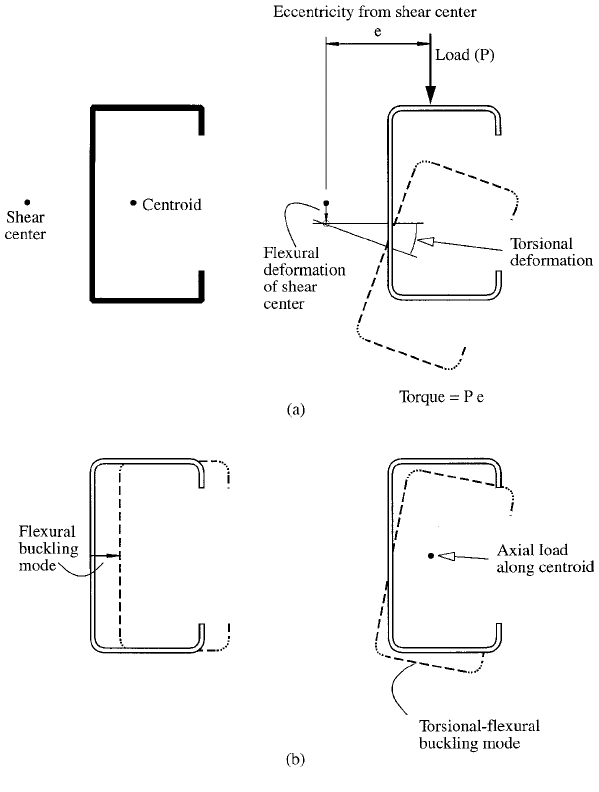
1.7.4 Propensity for Twisting

Cold-formed sections are normally thin, and consequently

they have a low torsional stiffness. Many of the sections

produced by cold-forming are singly symmetric with their

shear centers eccentric from their centroids, as shown in

Figure 1.13a. Since the shear center of a thin-walled beam

is the axis through which it must be loaded to produce

¯exural deformation without twisting, any eccentricity of

the load from this axis generally produces considerable

torsional deformations in a thin-walled beam, as shown in

Figure 1.13a. Consequently, beams usually require

torsional restraints at intervals or continuously along

them to prevent torsional deformations. Methods for

bracing channel and Z sections against torsional and

lateral deformations are found in Section D of the 1996

AISI Speci®cation and in Chapter 10 of this book.

For a column axially loaded along its centroidal axis,

the eccentricity of the load from the shear center axis may

cause buckling in the torsional-¯exural mode as shown in

Figure 1.13b at a lower load than the ¯exural buckling

mode, also shown in Figure 1.13b. Hence, the designer

must check for the torsional-¯exural mode of buckling

using methods described in Chapter 7 of this book and in

Section C4 of the AISI Speci®cation.

Beams such as channel and Z purlins and girts may

undergo lateral-torsional buckling because of their low

torsional stiffness. Hence, design equations for lateral-

torsional buckling of purlins with different bracing condi-

tions are given in Section C3 of the AISI Speci®cation and

are described in Chapter 5 of this book.

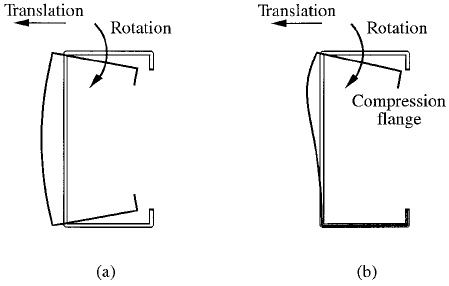
1.7.5 Distortional Buckling

Sections which are braced against lateral or torsional-

¯exural buckling may undergo a mode of buckling

commonly known as distortional buckling, as shown in

Figure 1.14. This mode can occur for members in ¯exure

Chapter 1

or compression. In the 1996 edition of the AISI Speci®ca-

tion, distortional buckling of edge-stiffened elements is

partially accounted for by Section B4.2. Further research

is underway to include speci®c design rules.

FIGURE 1.13 Torsional deformations: (a) eccentrically loaded

channel beam; (b) axially loaded channel column.

Introduction

1.7.6 Cold Work of Forming

The mechanical properties of sections made from sheet

steel are affected by the cold work of forming that takes

place in the manufacturing process, speci®cally in the

regions of the bends. For sections which are cold-formed

from ¯at strip the cold work is normally con®ned to the four

bends adjacent to either edge of each ¯ange. In these

regions, the material ultimate tensile strength and yield

strength are enhanced with a commensurate reduction in

material ductility. The enhanced yield strength of the steel

may be included in the design according to formulae given

in Section A7 of the AISI Speci®cation.

For cold-formed square or rectangular hollow sections,

the ¯at faces will also have undergone cold work as a result

of forming the section into a circular tube and then rework-

ing it into a rectangle or square. In this case, it is very

dif®cult to compute theoretically the enhancement of yield

strength in the ¯ats, so the AISI Speci®cation allows the

measured yield strength of the steel after forming to be

used in design where the yield strength is determined

according to the procedures described in ASTM A500. The

distribution of ultimate tensile strength and yield strength

FIGURE 1.14 Distortional buckling modes: (a) compression; (b)

¯exure.

Chapter 1

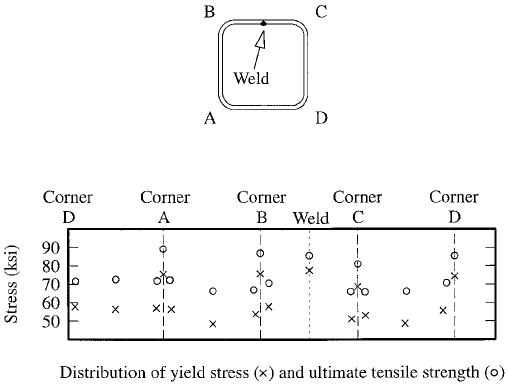
measured in a cold-formed square hollow section is shown

in Figure 1.15. The distribution indicates that the proper-

ties are reasonably uniform across the ¯ats (except at the

weld location) with a yield strength of approximately 57 ksi

for a nominal yield stress of 50 ksi. This is substantially

higher than the yield strength of the plate before forming,

which is normally approximately 42 ksi. The enhancement

of the yield stress in the corners is very substantial, with an

average value of approximately 70 ksi.

1.7.7 Web Crippling Under Bearing

Web crippling at points of concentrated load and supports

can be a critical problem in cold-formed steel structural

members and sheeting for the following reasons:

1. In cold-formed design, it is often not practical to

provide load bearing and end bearing stiffeners.

FIGURE 1.15 Tensile properties in a cold-formed square hollow

section (Grade C to ASTM A500).

Introduction

This is always the case in continuous sheeting and

decking spanning several support points.

2. The depth-to-thickness ratios of the webs of cold-

formed members are usually larger than for hot-

rolled structural members.

3. In many cases, the webs are inclined rather than

vertical.

4. The load is usually applied to the ¯ange, which

causes the load to be eccentric to the web and

causes initial bending in the web even before

crippling takes place. The larger the corner

radius, the more severe is the case of web crip-

pling.

Section C3.4 of the AISI Speci®cation provides design

equations for web crippling of beams with one- and two-

¯ange loading, stiffened or unstiffened ¯anges, and

sections having multiple webs.

At interior supports, beams may be subjected to a

combination of web crippling and bending. Section C3.5

provides equations for this condition. Likewise, such

sections may be subjected to a combination of shear and

bending. Section C3.3 covers this condition.

1.7.8 Connections

A. Welded Connections

In hot-rolled steel fabrication, the most common welds are

®llet welds and partial or complete penetration groove

welds. There is a much wider variety of welds available

in cold-formed construction, such as arc spot welds (some-

times referred to as puddle welds), ¯are bevel groove welds,

resistance welds, etc. In hot-rolled welding, generally the

two pieces being joined are close to the same thickness, so it

is easy for the welder to set the amperage on his welding

machine. In cold-formed steel, there is often a great differ-

ence in the thicknesses of the pieces being joined. For

Chapter 1

example, welding a 22 gauge deck to a

-in. beam ¯ange

requires completely different welding skills. To get enough

heat to fuse the thick ¯ange means that the thin sheet may

be burned through and if there is not intimate contact

between the two pieces, a poor weld will result. In these

cases, weld washers, thicker than the sheet, may be used to

improve weld quality.

Another difference between hot-rolled welding and

light-gauge welding is the presence of round corners. In

welding two channels back-to-back, for example, there is a

natural groove made by the corner radii and this can be

used as a repository for weld metal. Such welds are called

¯are bevel groove welds.

Tests of welded sheet steel connections have shown

that failure generally occurs in the material around the

weld rather than in the weld itself. Provisions for welded

connections are found in Section E2 of the AISI Speci®ca-

tion and are discussed in Chapter 9.

B. Bolted Connections

Bolted connections in cold-formed construction differ

primarily in the ratio of the bolt diameter to the thickness

of the parts being joined. Thus, most bolted connections are

controlled by bearing on the sheet rather than by bolt

shear. The ``net section fracture'' that is usually checked

in heavy plate material rarely occurs. Provisions for bolted

connections appear in Section E3 and are discussed in

Chapter 9.

C. Screw Connections

Self-drilling screws, self-tapping screws, sheet metal

screws, and blind rivets are all devices for joining sheet to

sheet or sheet to heavier supporting material. Of these, the

self-drilling screw is the most common for structural appli-

cations. It is used for securing roof and wall sheets to

purlins and girts and making connections in steel framing

for residential or commercial construction. Sheet metal

Introduction

screws and rivets are mostly used for non-structural appli-

cations such as ¯ashing, trim, and accessories. Pullover

and pullout values for screws may be calculated with the

equations in Section E4 or values may be obtained from the

manufacturer. The design of screw connections is discussed

in Chapter 9.

D. Clinching

A relatively new method for joining sheets is called clin-

ching. No external fastener is used here; a special punch

deforms the two sheets in such a way that they are held

together. At this time, no provisions for determining the

capacity of this type of connection exist in the AISI Speci-

®cation, so the testing provisions of Section F of the AISI

Speci®cation should be used.

1.7.9 Corrosion Protection

The main factor governing the corrosion resistance of cold-

formed steel sections is not the base metal thickness but

the type of protective treatment applied to the steel. Cold-

formed steel has the advantage of applying protective coat-

ings to the coil before roll forming. Galvanizing is a process

of applying a zinc coating to the sheet for corrosion protec-

tion and is purely functional. A paint ®nish on steel can

serve as corrosion protection and provide an attractive

®nish for exterior panels. A painted or galvanized coil can

be passed through the rolls and the ®nish is not damaged. A

manufacturer of exterior panels can now order coils of steel

in a variety of colors and the technology of the factory ®nish

has improved to the point that the paint will not crack

when a bend is made in the sheet.

Other than paint, the most common types of coatings

for sheet steel are zinc (galvanizing), aluminum, and a

combination of zinc and aluminum. These are all applied

in a continuous coil line operation by passing the strip

through a molten metal bath followed by gas wiping to

control the amount of coating applied. Typical coating

Chapter 1

designations are G60 and G90 for galvanized product and

T2 65 and T2 100 for aluminum-coated sheet. The numbers

in these designations refer to the total coating weight on

both sides of the sheet in hundredths of an ounce per

square foot (oz=ft

) of sheet area. For example, G60

means a minimum of 0.60 ounce of zinc per square foot.

This corresponds to a 1-mil thickness on each side. A G90

coating has 0.90 ounce per square foot and a thickness of

1.5 mils (Ref. 1.9).

1.7.10 Inelastic Reserve Capacity

Generally, the proportions of cold-formed sections are such

that the development of a fully plastic cross-section is

unlikely. However, there is a provision in Section

C3.1.1(b), Procedure II, that permits the use of inelastic

reserve capacity for stockier sections, such as those found

in rack structures. Here, compressive strains up to three

times the yield strain are permitted for sections satisfying

certain slenderness limits. In this case, the design moment

may not exceed the yield moment by more than 25%.

1.8 TWO DESIGN METHODS

The 1996 AISI Speci®cation for Cold-Formed Steel

Members is a unique document in that it simultaneously

satis®es those wishing to use the time-tested allowable

stress design (ASD) method and those wishing to use the

more modern load and resistance factor design (LRFD)

method. At the same time, all the equations in the speci®-

cation are formulated in such terms that any system of

units may be used. Thus, four permutations are available

in one reference:

ASD with customary or English units

ASD with SI units

LRFD with customary or English units

LRFD with SI units

Introduction