Hall A.S., Archer F.E., Gilbert R.I. Engineering Statics
Подождите немного. Документ загружается.


free
surface
Since the whole body of water
is
at rest, the forces on the vertical sides of the prism
are everywhere horizontal. Hence the weight Wmust be e~uilibrated by the upward
pressure on the base. If the pressure at depth
y
is
p,
the resultant force on the base
is:
F
=
p.A
Hence:
PA
=
YAY
and
P
=
YY
Pascal formulated a law which states that at any point within a fluid at rest the pressure
is the same in all directions. This law, together with Equation
14.3
and the definition of
a fluid, tells us that the pressure on any subme
d
body at depth
y
below the free surface
is
y
y
and acts normal to the surface of the b
In
the remainder of this chapter, fre~uent referenc ill be made to the
append^
of
this book, and it is essential that this Appendix be re conj~lnction with the present
chapter.
onsider first the pressure on a horizontal surface of area
A,
Ev
at the same depth below the free water surface and the pressure
force on the surface is
I;
=
y
y
A,
This resultant force acts at
t
(see Appendix, Section
A.
l).
As
an. example of water pressure
on
a vertical plane,
we
consi
water on the vertical face of a darn (Fi

I
Y
I
The resultant force on a
1
m length of the dam may be calculated as the volume of the
pressure intensity diagram, shown in side elevation in Figure
14.2.
Thus:
h
2
I;=
yhx-X
1
=0.5yh2
This force acts not at the centroid of the
darn
wall but at the level of the centroid of
the triangular pressure intensity diagram
of
Figure
14.2,
i.e. at
2h13
below the free water
surface,
as
shown.
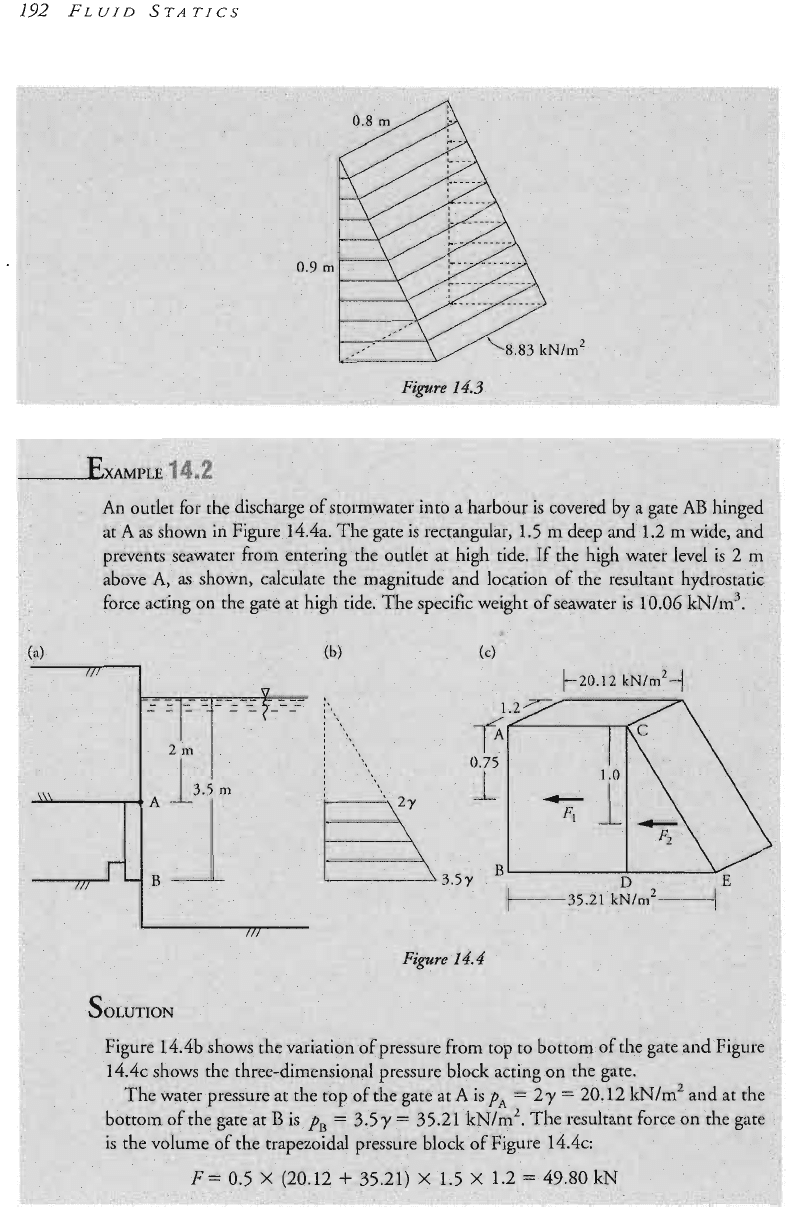

For surfaces of simple shapes such
as
those of Examples
14.1
and
14
force
is
easily found by c~culatin~ the volume of the pressure
block.
F
shapes the reader
is
referred to Section
A2
of the Appendix. There it
is
linearly
va~in~
pressure acts upon a plane surface of area
A,
the resuitant force
is
equal
to the pressure at the centroid of the surface times the area
A.
Thus
if
the centroid
is
at
a
depth
yc
below the free surface, the resultant force
is
(see Equation
A,
1
I):
p=
YycA
The point through which the resultant acts
is
called the
centre
o~~~ess~~~
an
is
denoted by
yep.
From Equation
A.27,
we have:
where
is
the second moment
of
area of the surface c~cu~ated about a hori~ont~
ais
through its centroid.

E~u~tion
14.6
shows
that the centre of pressure always occurs at a
the centroid
of
the surface on which the hydrostatic pressure acts.
eween the centre
of
pressure and the centroid
&./Ayc
decreases
as
the
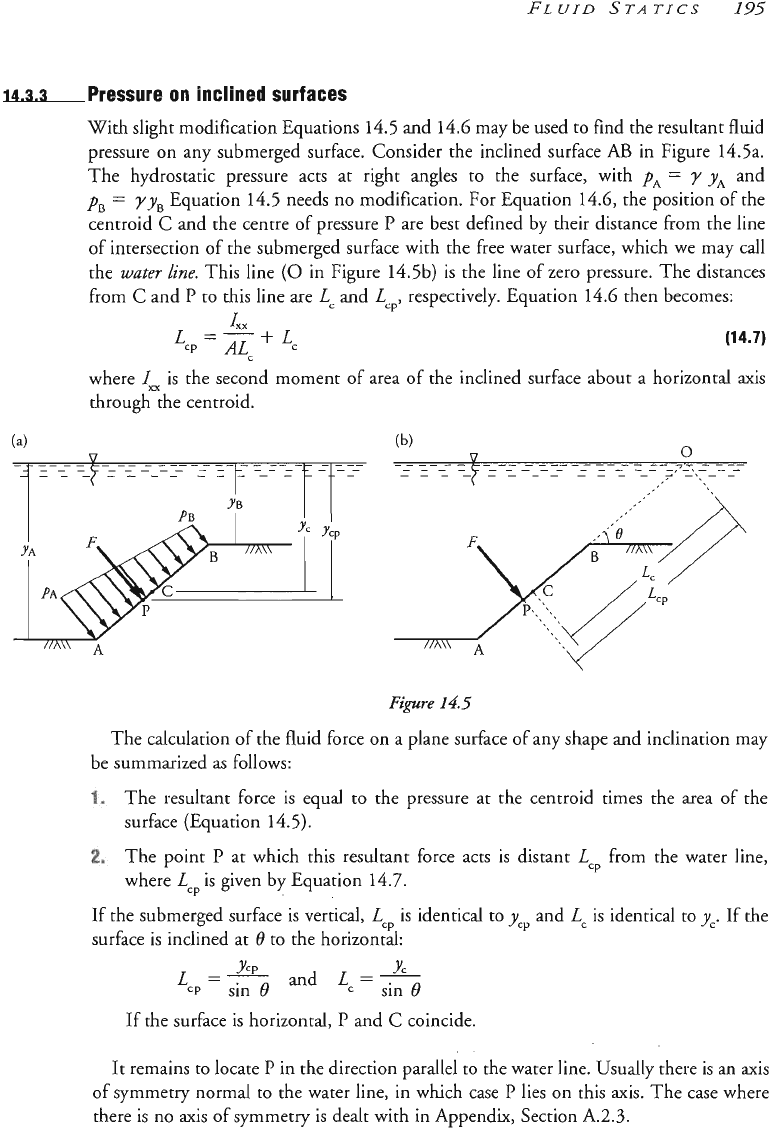
With slight modification Equations 14.5 and
14.6
may be used to find the resultant fluid
pressure on any submerged surface. Consider the inclined surface
AB
in Fi
The hydrostatic pressure acts at right angles to the surface, with
p,
=
y
y,
and
pB
=
yyB
Equation 14.5 needs no modification. For Equation 14.6, the position of the
centroid
C
and the centre of pressure
P
are best defined by their distance from the line
of
intersection of the submerged surface with the free water surface, which we
may
call
the
~~te~
line.
This line
(0
in Figure 14.5b)
is
the line of zero pressure. The distances
from
C
and
P
to this line are
LC
and
Lcp,
respectively. Equation 14.6 then becomes:
1
LCP
=
=
1-
LC
ALC
where is the second moment of area of the inclined surface about
a
horizontal axis
through the centroid.
The calculation of the fluid force on a plane surface of any shape and inclination may
be summarized
as
follows:
The resultant force
is
equal to the pressure at the centroid times the area of the
surface (Equation 14.5).
The point
P
at which this resultant force acts is distant
Lcp
from the water line,
where
LC,
is given by Equation 14.7.
d surface is vertical,
Lcp
is identical to
yCp
and
LC
is identical to
yC.
If the
surface is inclined at
t)
to the horizontal:
L,
=-------
"'
and
LC
==
-
=P
sin
0
sin
0
YC
If
the surface
is
horizontal,
P
and
C
coincide.
It
remains to locate
P
in the direction parallel to the water line. Usually there
is
an axis
of sym~et~ normal to the water line, in which case
P
lies
on
this axis. The case wh
there is no axis of symmetry is dealt with in Appendix, Section
A.2.3.
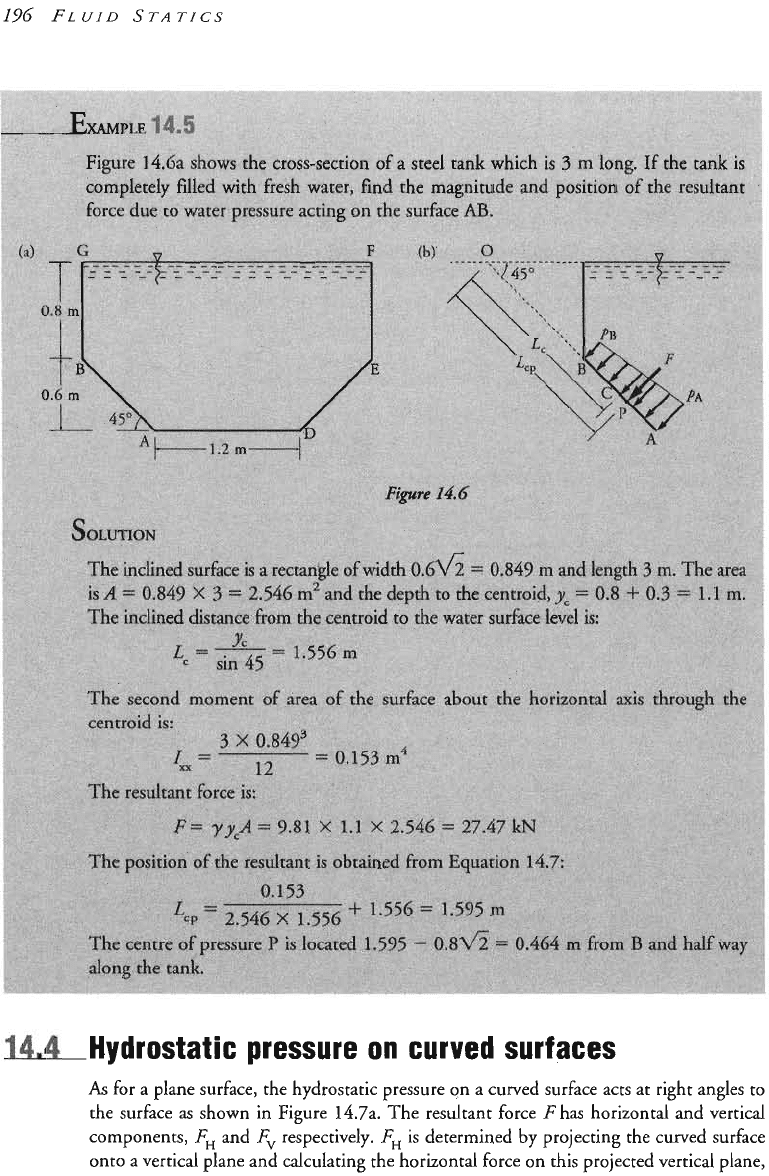
As
for a plane surface, the hydrostatic pressure on a curved surface acts at right angles to
the surface
as
shown in Figure
14.7a.
The resultant force
F
has horizontal and vertical
components,
FH
and
F,
respectively.
FH
is determined by projecting the curved surface
onto
a
vertical plane and calculating the horizontal force on this projected vertical plane,
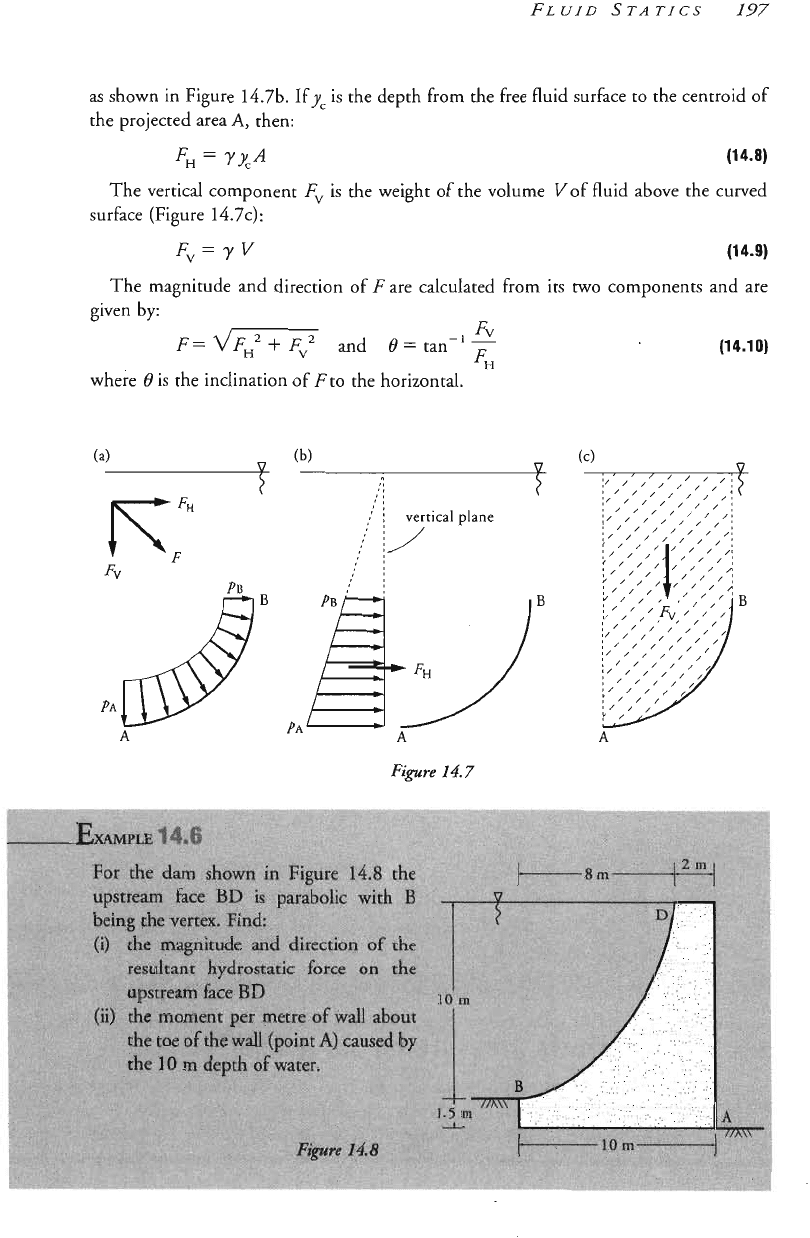
as shown in Figure 14.7%.
Ify,
is the depth from the free fluid surface to the centroid
of
the projected area
A,
then:
FE1
==
rxn
The vertical component
Fv
is the weight of the volume Vof fluid above the curved
surface (Figure
14.7~):
F,==
yV
The ~agnitude and direction of
F
are calculated from its
two
components and are
given by:
F
=
m
and
(3
=
tan-'
-
FV
FH
where
8
is
the inclination
of
F
to the horizontal.
A
B
PA
A
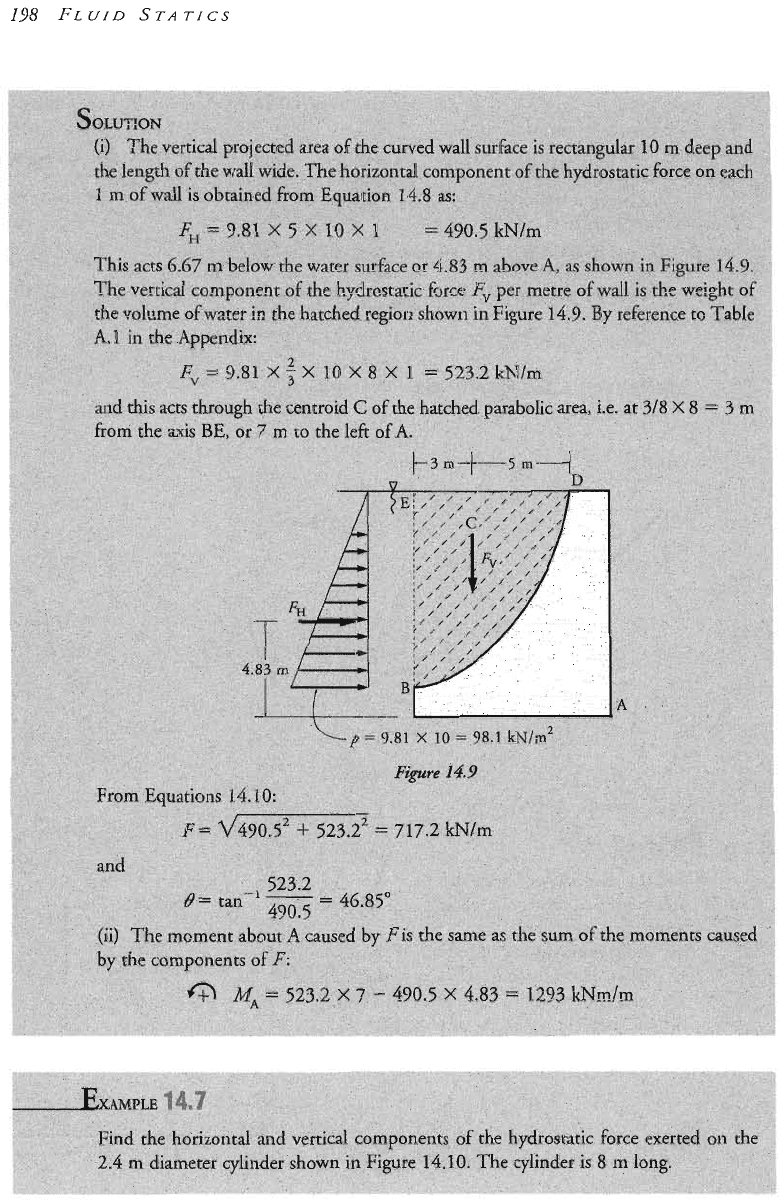
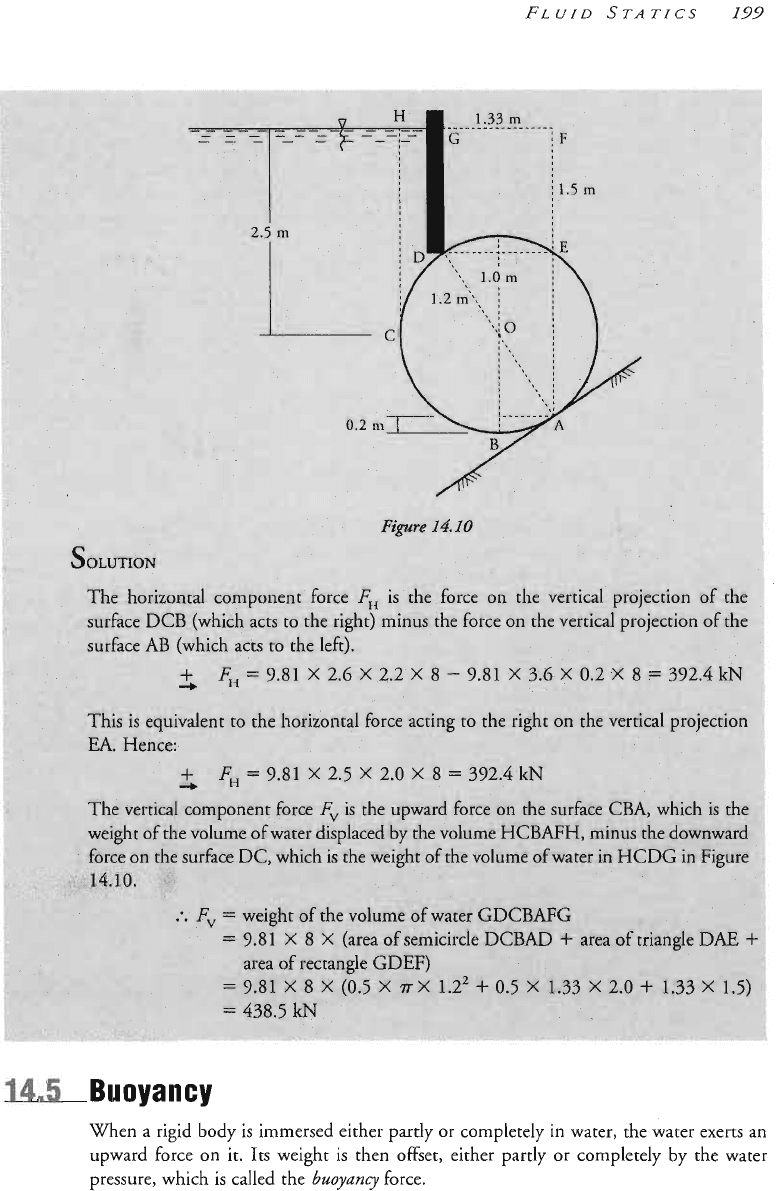
en a rigid body is immersed either partly or completely in water, the water exerts an
upward force
on
it,
Its
weight
is
then of-fset, either partly or completely by the water
pressure, which
is
called the
buoyancy
force.
