Hall A.S., Archer F.E., Gilbert R.I. Engineering Statics
Подождите немного. Документ загружается.

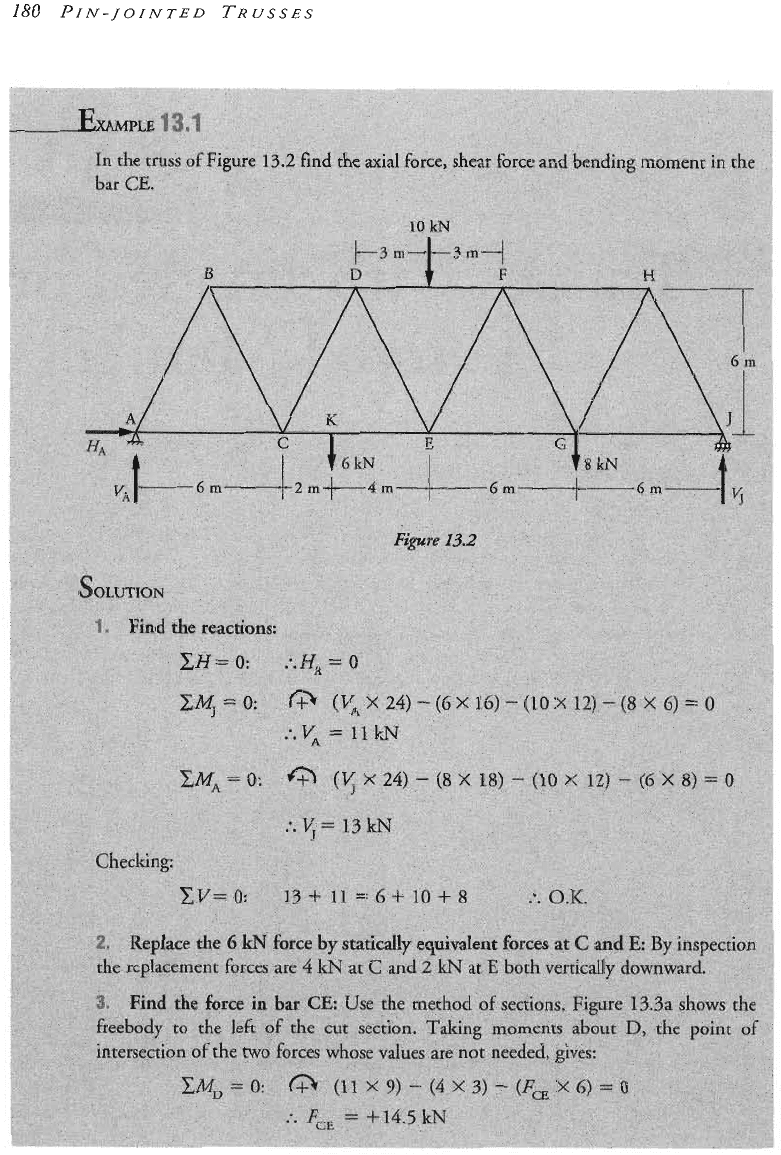

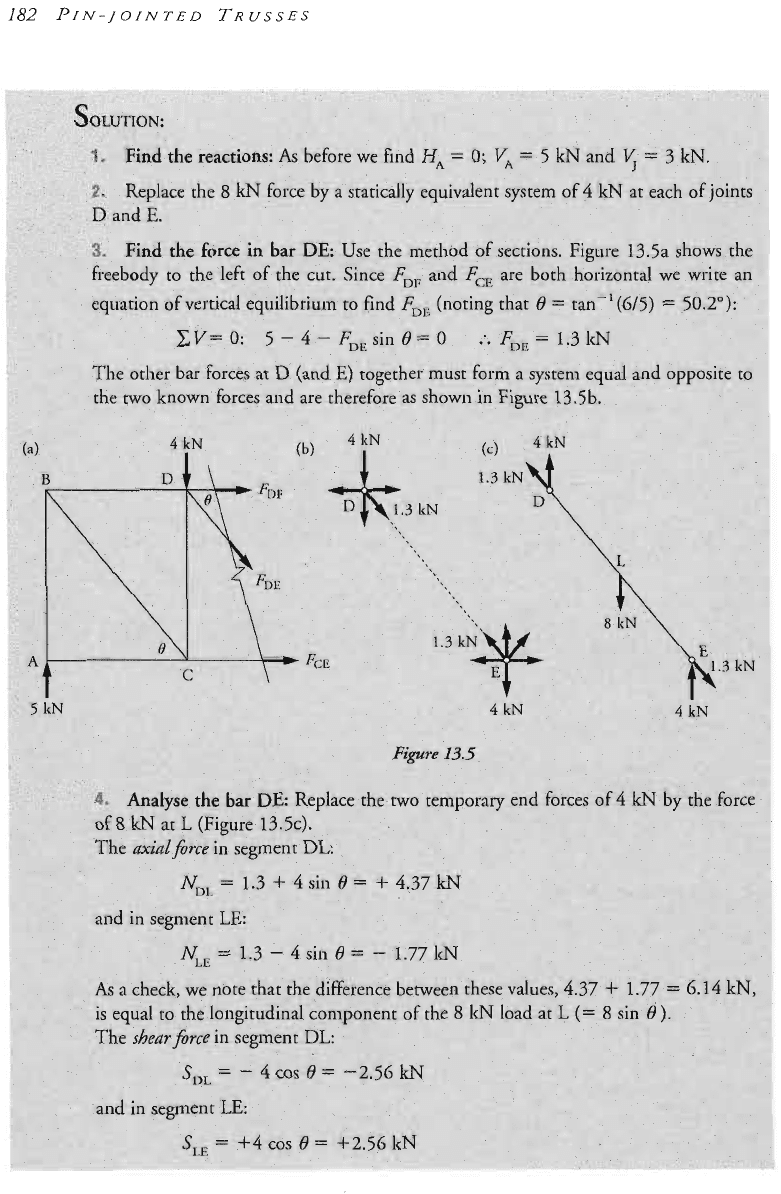

Very rarely it may be necessary to analyse a truss having a member which
is
either curved
or kinked, such as AB in Figure
13.6.
Since the member is in e~uilibrium under the
action
of
the
TWO
end forces, these forces must act in the direction
of
the straight line AB.
If
the actual member does not lie along this line then these end forces will cause bending
moments and shear forces within the member, in addition to
axial
force. These internal
actions can be calculated by the methods of Chapter
7.
The out-of-strai~htness of
member AB does not affect the analysis of the truss
as
a whole.
Find the axial force in each member of the truss shown in Figure
P13.1
In the case
of
the loaded members find also the bending moment at the point of application of the
load.
B
C
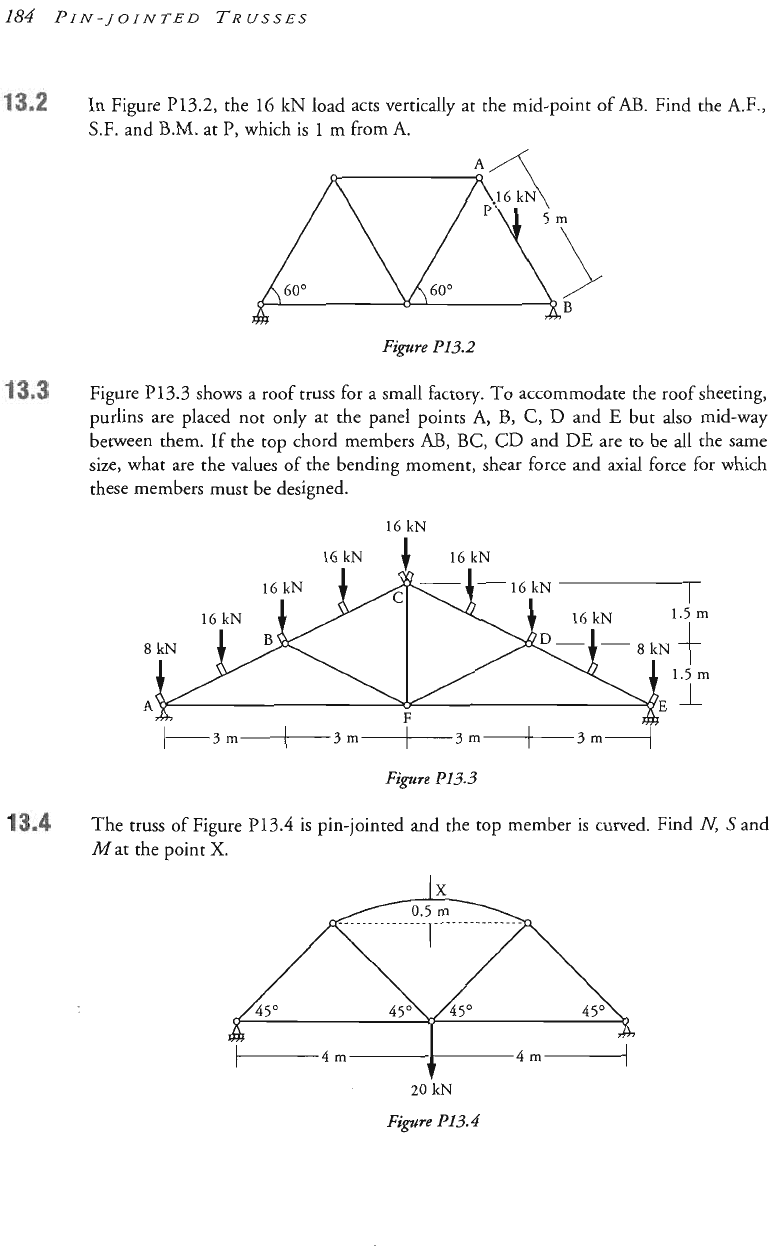
In Figure P13.2, the 16
kN
load acts vertically at the mid-point of AB. Find the A.F.,
S.F. and
B.M.
at
P,
which
is
l
m from
A.
Fipre
P13.2
Figure P13.3 shows a roof truss for a small factory.
To
accommodate the roof sheeting,
purlins are placed not only at the panel points
A,
B, C,
D
and E but
also
mid-way
between them. If the top chord members AB, BC, CD and DE are to be all the same
size, what are the values of the bending moment, shear force and axial force for which
these members must be designed.
16
kN
16
kN
16
kN
8
A
Fipre
P13.3
The truss
of
Figure P13.4 is pin-jointed and the top member is curved. Find
N:
S
and
Mat the point
X.
IX
This Page Intentionally Left Blank




The branch of mechanics deal with the behaviour of fluids at rest or in motion is
known as
~~~~
~ec~~~~cs.
That
t
of fluid mechanics which is concerned with fluids at
rest (or in equili~rium) is called
~~i~
statics,
Fluid statics involves the study of pressure
and its variation throu
t
a fluid. It also involves the calculation of forces exerted by
a fluid on the surfaces uctures with which it
is
in contact, In the case of a flui
rest, the property that affects the pressure variation is the specific weight or we
density
y
which is the we
The previous parts of with ~o-dimensional statics.
forces and the structures have been essentially coplanar. It is not possible to
fluids as ~o-di~ensional, but the force systems considered in this chapter are such that
there should be no difficulty in applying the principles of previous chapters. Three-
dimension^
systems of a more general nature will be dealt with in Part
5.
In problems associated with civil and environmental en
commonly encountered is water. The specific weight of fresh
re~ainder of this chapter will be written in terms of water, but the same principles apply
to any other fluid (using an appropriate value of
y
).
may be defined as a substance that deforms continuously when sL~bjected to a
rce. In
a
fluid at rest, therefore, no shear forces exist. This implies that no forces
ntial to a submerged surface. The only forces actin
es normal to these surfaces.
This definition leads to the direct solution of many problems. In the first place, it
allows us to determine the water pressure at any depth. Consider a prism of water with
vertical sides and with horizontal cross-section of area
A,
which
is
part of a lar
of water (Figure
14.
l).
The prism extends from the free surface of the water (i.e. the
surface where the water pressure is zero) down to a depth
y.
The volume of water
enclosed within this ima~inary boundary is
Ay
and therefore its weight is:
