Hall A.S., Archer F.E., Gilbert R.I. Engineering Statics
Подождите немного. Документ загружается.



thods of the last chapter, the equilibrium of each joint is considered
.
If the force in particular members is required it may be often more
o
use the method of sections. This procedure is rather similar to that used
e internal actions at a articular cross-section of a beam.
Suppose that in the truss of Figure
12.1
the force in GE is required. The truss is cut
by a plane which passes through
CE
and the equilibrium of one part of the truss is
considered, The freebody to the left of the cut for instance, is acted upon by the known
forces
V
and
Wl
and the unknown forces in the cut bars, which may be denoted by
X
It has been shown that when the external loads act at the joints, the force in
her acts along the strai
t
line joining the ends of the member, hence the lines
of action of
X
Yand are lcnown, and the forces can be found from the equations of
equilibrium.
The method is subject to certain limitations, If the number
of
cut members exceeds
three, some of the unknowns cannot be found. Even in this case, one unknown can be
found if all
of'
the others happen to be concurrent. If three members only are cut their
forces can be found provided the members are not concurrent, for in this case only
two
equations are available.
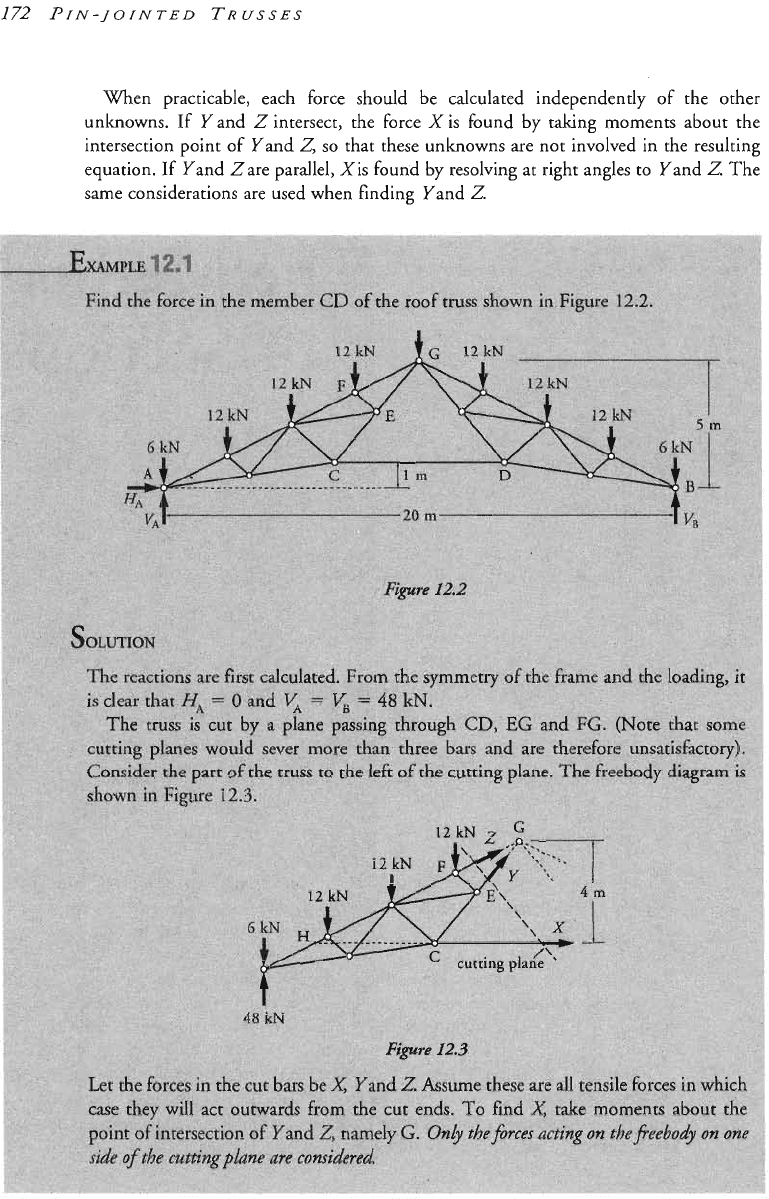
When practicable, each force should be calculated independently of the other
unknowns. If
Y
and
Z
intersect, the force
X'
is
found by taking mo~ents about the
intersection point of Yand
Z
so
that these unknowns are not involved in the resulting
equation.
If
Yand Zare parallel, Xis found by res ing at right angles to Yand
same considerations are used
when
finding Yand

Trusses and beams have much in common both
as
regards their function and their
analysis,
A
beam
is
used to span a gap between supports and to carry loads.
A
truss may
be employed for the same purpose, being usually chosen when the span becomes too
large for a beam to be economical. Certain points
of
similarity can be seen with reference
to trusses with parallel chords.
In a truss of the type shown in Figure
12.4
the horizontal members are known
as
c~u~~s,
and the remainder are called
web
~e~be~s.
In the following example, the truss
is
compared with a solid beam spanning between the points
A
and
N,
which will be
referred to
as
the analogous beam
AN.

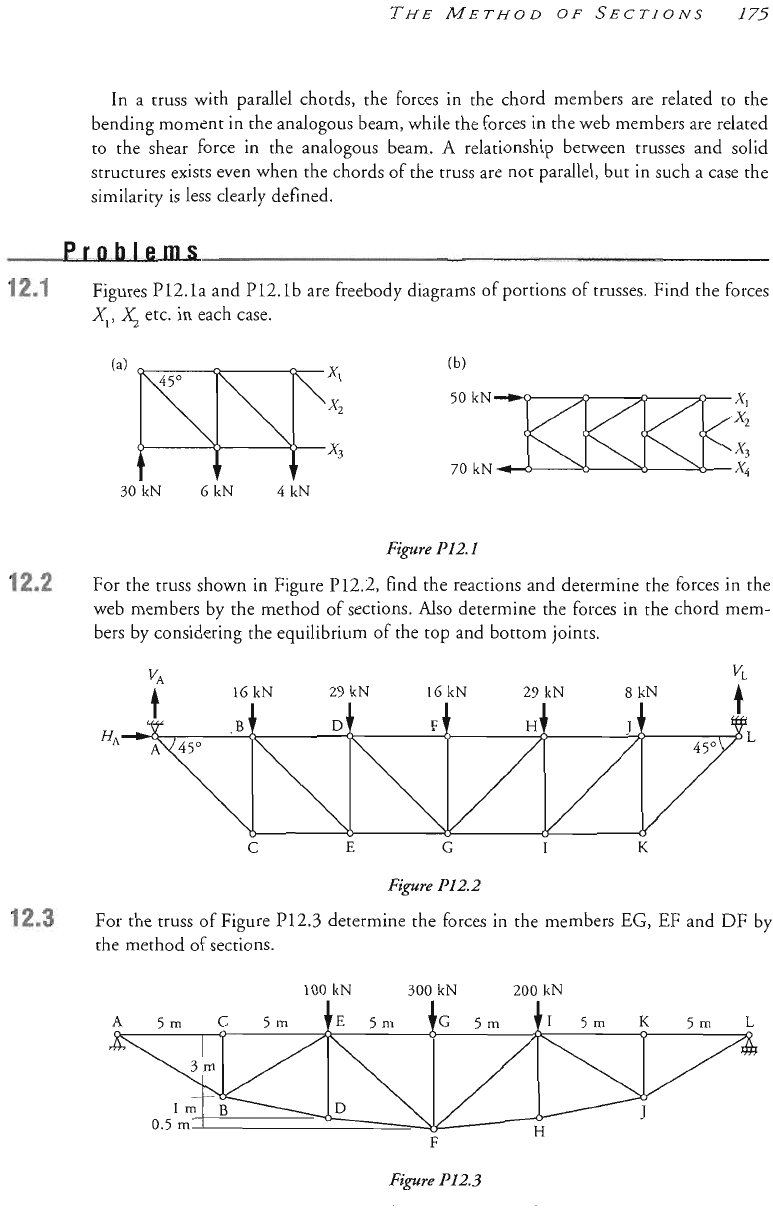
30kN
6
kN
4
kN
For
the truss
of
Figure
P1
the
method
of
sections.
100
kN
300
kN
200
kN
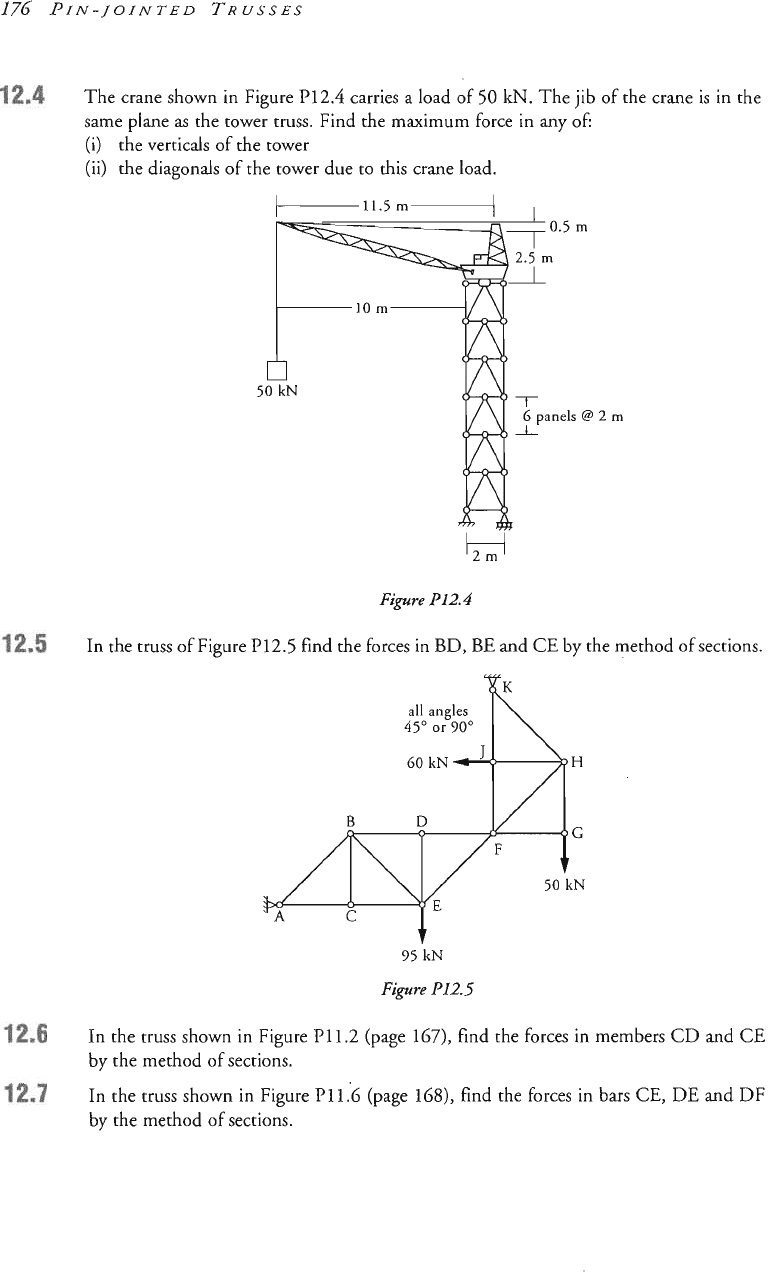
The crane shown in Figure
P124
carries a load of
50
lane as the tower truss. Find the ~~imum for
(i)
the verticals of the tower
(ii)
the diagonals
of
the tower due to this crane load.
2m
In
the truss of Figure
P12.5
find the forces in
BD,
BE
and
CE
by
the method of sections.
95
kN
the truss shown in Fi
167),
find the forces in
embers
C
the method of sections.
n the truss shown in Figure
P1
1
.G
(pa
),
find the forces
in.
bars
CE,
by the method of sections.
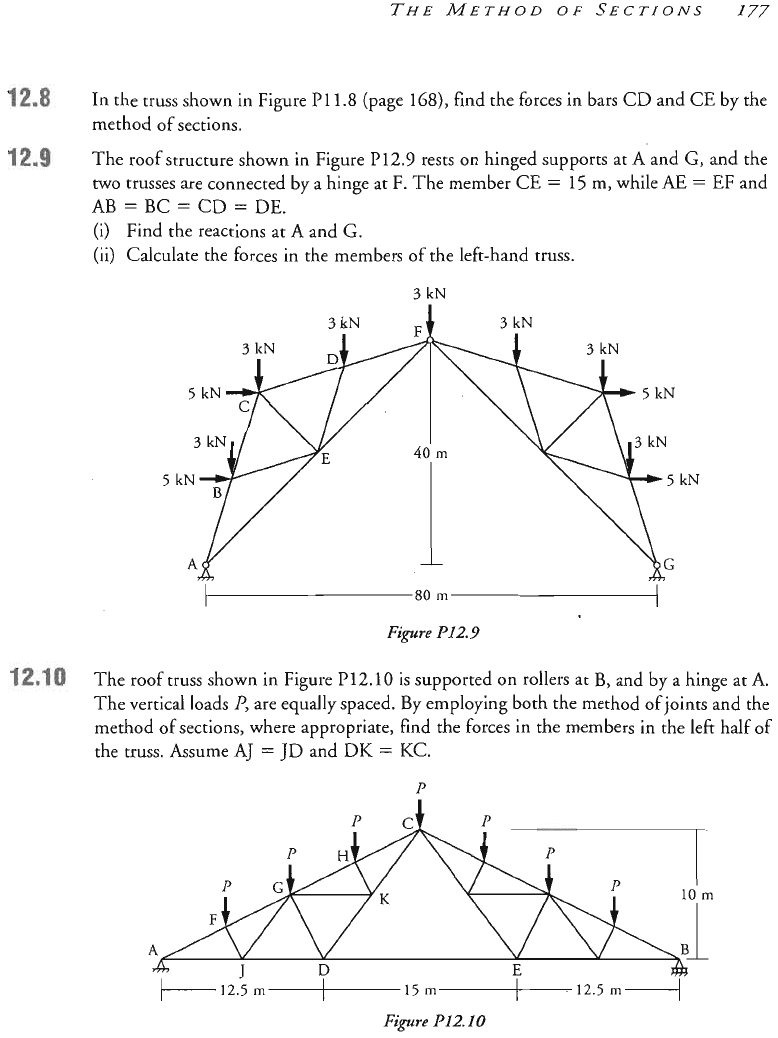
In the truss shown in Figure
P1
1.8
(page
168),
find the forces in bars
CD
an
method of sections,
The roof structure shown in Figu
P12.9
rests
on.
hinged supports at
A
and
G,
and the
es are connected by a hi at
F.
The member
CE
=
15
m,
while
(i) Find the reactions at
A
and
G.
(ii) Calculate the forces in the members of the lek-hand truss.
3
kN
The
roof
truss shown in Fi re
P12.10
is supported on rollers at
The vertical loads
P,
are eq
.
By employing both the me
method of sections, where find the forces in the mem
the truss, ~sume
AJ
=
JD
and
DK
=
KC.
P
P


If external loads are not applied directly to the joints but to
a
member of the truss, then
that member performs a ual function. Firstly,
it
acts as
a
beam
spannin
joints at each end of the member, and serves to transfer the loads to these adjacent joints.
In this capacity it will be subjected to bending moments, shear forces and in some cases
axial forces. Secondly, it acts as
a
member of the truss. In this capacity it sustains an axial
force which is deter~ined by the methods of Chapters
1
1
and
12.
note that if the loads on a particular bar in a truss are replaced by
ent system, then all bar forces outside the region of chan
Qz
B
I
I
For example, consider the bar CD
of
Figure
13.1
loaded by a
sin
is
in equilibrium under the action of the load
P
and the bar forc
exerted by adjacent bars.
if
the force
P
is replaced by forces
is
P,
then the forces
F,,
F,
etc. remain unchanged. If
Ql
and
Qz
act at the joints
C
and
D,
the truss is now loaded at the joints only and may be analysed by the methods of the
previous chapters,
If an analysis of bar
CD
alone is required, it is often possible by using the method
of
sections. This will not give the values of the individual forces
Fl,
F,
etc. but it will give
their resultant, which is all that is required in this case. The procedure will be illustrated
by
two
examples.
