Hall A.S., Archer F.E., Gilbert R.I. Engineering Statics
Подождите немного. Документ загружается.


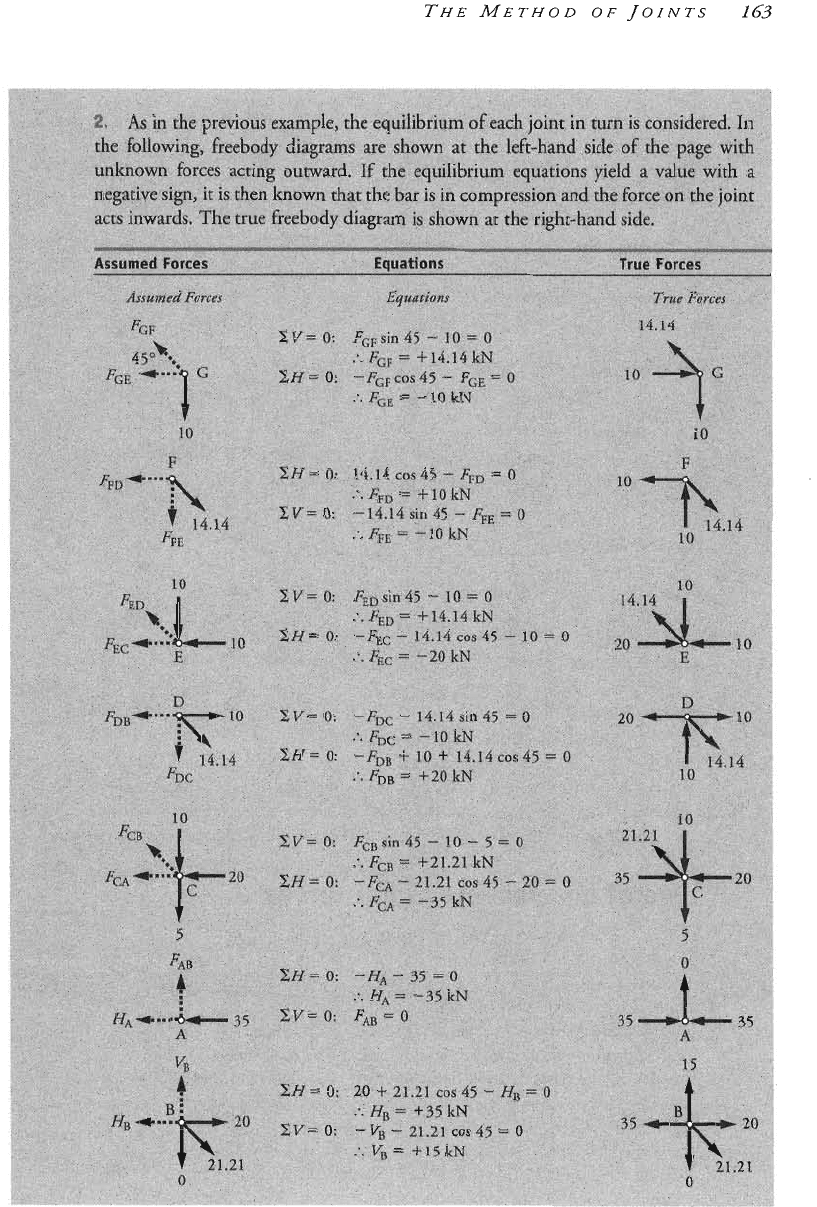
it by the joints at each end. Each pin is in equilibrium under the action of the forces
exerted upon it by the adjacent bars and the external loads (applied forces or reactions).
In the cases considered here, where the external
loads are all applied at the joints, each bar is in
equilibrium under the action of the two forces
exerted on it by the joints at its ends. These
two
forces must therefore be equal and opposite and
must act along the line joining the joints, as shown
in Figure
11.2.
BA
Each pin in a truss is in equilibrium under the action of the forces applied to it by the
surrounding bars together with the external loads, if any, acting at that joint. For the
present case (trusses in which all external loads act at joints), the forces exerted by the
bars upon a given pin act in the direction of the lines joining the given pin with its
neighbours,
so
that the directions of
all
forces are known. The forces at a given pin form
a concurrent system, implying
two
equilibrium conditions,
In the method of joints, each joint in turn is considered
as
a freebody, The
two
equations of equilibrium are used to express the relationships between the known and
unknown forces at the joint. The unknown forces at a joint can be determined provided
that there are not more than
two
such forces.
This is exactly the problem discussed in Section
3.2
(see Example
3.3
page
21).
Note
that a bar in tension exerts an outward force on the joint, while a bar in compression
exerts an inward force. In the freebody diagram of any particular joint, known forces are
shown with the appropriate direction. ~nknown forces are assumed to be tensile and
shown as outward arrows, Solution of the equilibrium equations will then result in a
positive sign (confirming tension) or a negative sign (indicating compression).



It is helpful to imagine how this truss would collapse if a particular member was
S
to the concept of the function of the member
(
as either keeping
two
joints apart (compression)
os
holding them
of
these forces.
It
is
often quicker to use these components
as
the
unknown quantities and to calculate the actual bar forces later,
The
x
and
y
Components of a bar force are proportional to the
x
and
y
projections of the bar length, and these dimensions are
usually the ones given on the drawin
f
the truss. In Figure
1
1
.7,
the bar
GM
has projections
of
2
and
5
m.
Suppose the
S
component of the force exerted by GM on joint G has been
determined as
16
kN?
acting away from the ‘oint. It follows that the
y
component is
I6
X
512
=
4.0
kN
also
act away from the joint.
c;
At
the other end
M
the force Components


For trusses with parallel chords, this method allows the truss to be solved without the
need to write the equations down. For a truss with an inclined chord, such
as
a
roof truss,
F’
==
O
at
a
joint will produce
two
simultaneo~s equations.
Even
so,
it may still be quicker to write these in terms of components rather than the
actual bar forces.
For the truss
of
Figure
reactions and determine
members of the truss,
P1l.l,
find the
the forces in the
40
kN
80
kN
40
kN
V1
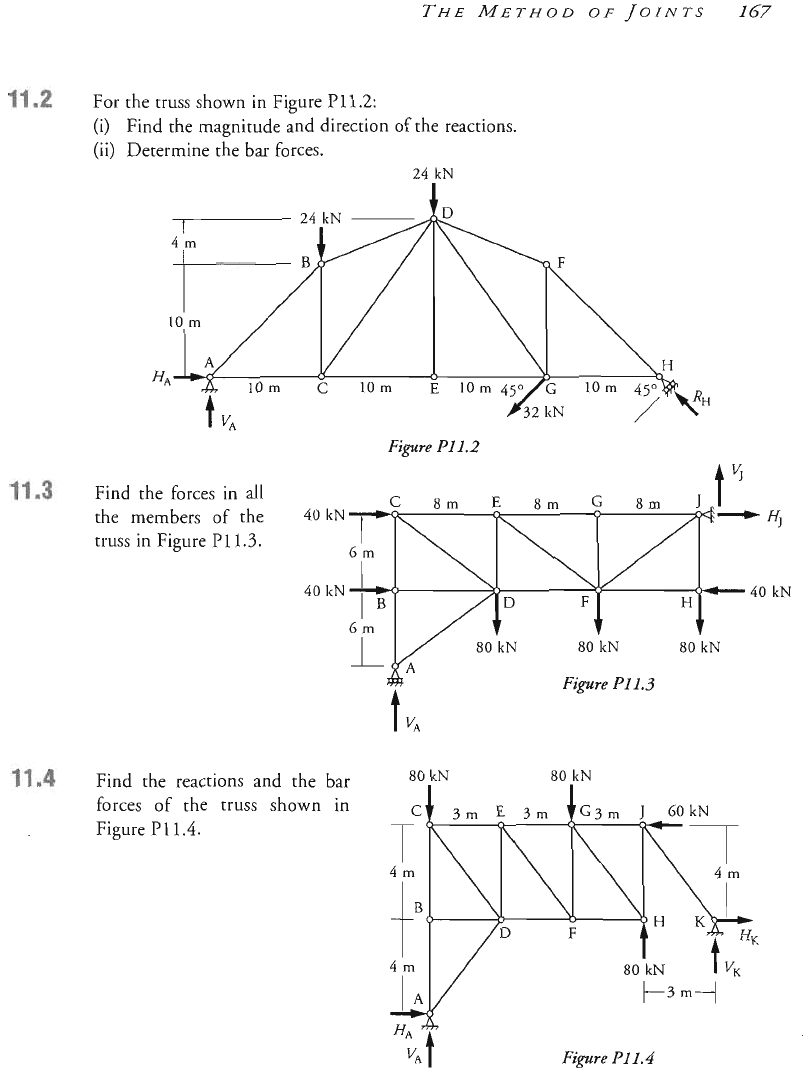
or the truss shown in Figure
P1
l.
irection
of
the reactions.
24
kN
7
24
4m
the forces in
all
members of the
40
IcN
truss in Figure
P
l
l.
40
IrN
Find the reactions and the
bar
forces of the truss shown in
Figure
PI
l
.4.
80
kN
80
kN
80
kN
80
kN
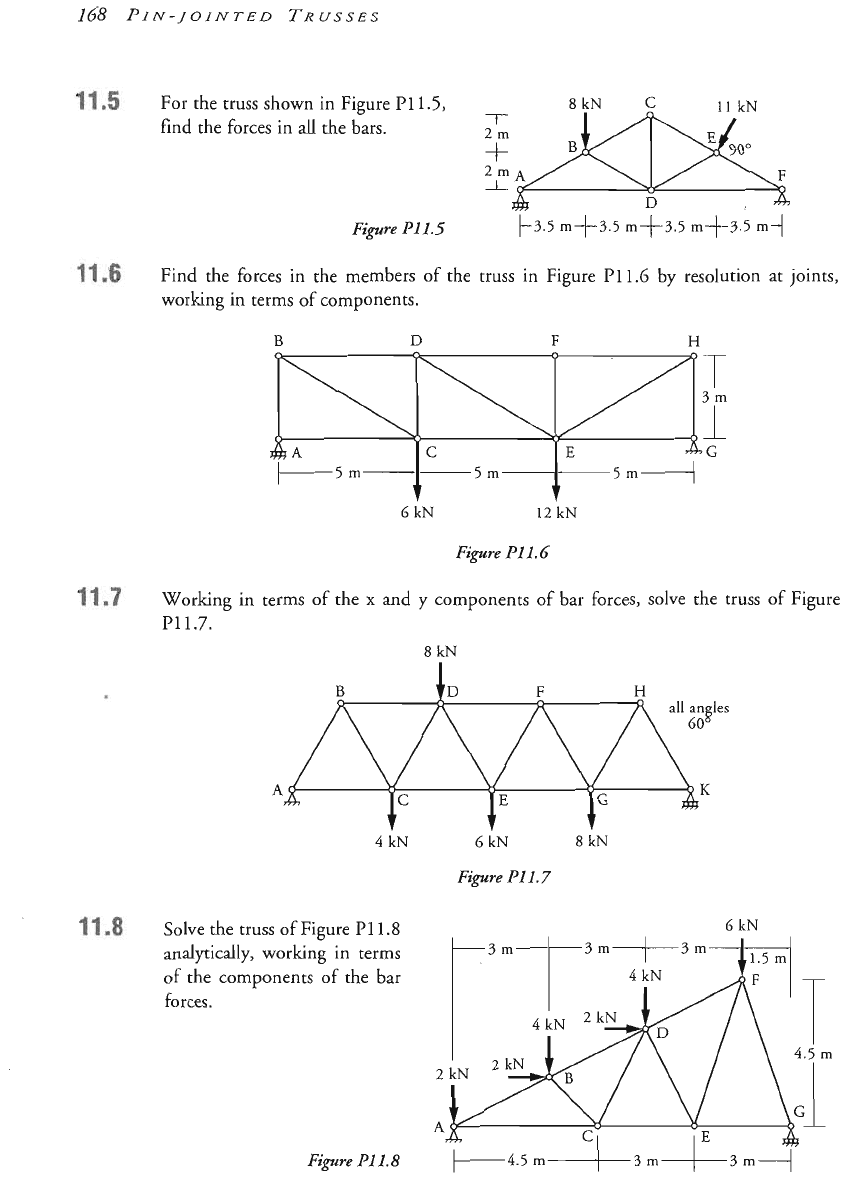
For the truss shown in Figure P1
1.5,
find the forces in all the bars.
2m
"t
2m
Fipre
Pl
l.
5
Find the forces in the members of the truss in Figure P1
1
.G
by resolution at joints,
working in terms of components.
B
D
F
H
6 kN
12
kN
Working
in terms of the
x
and y components of bar forces, solve the truss of Fi
P1
1.7.
8
kN
4
kN
Solve the truss of Figure
P1
1
.8
analytically, working in terms
of the components of the bar
forces.
6
kN
Fipre
Pl
l.
8
/------4.5
m,~3
m~-3
m
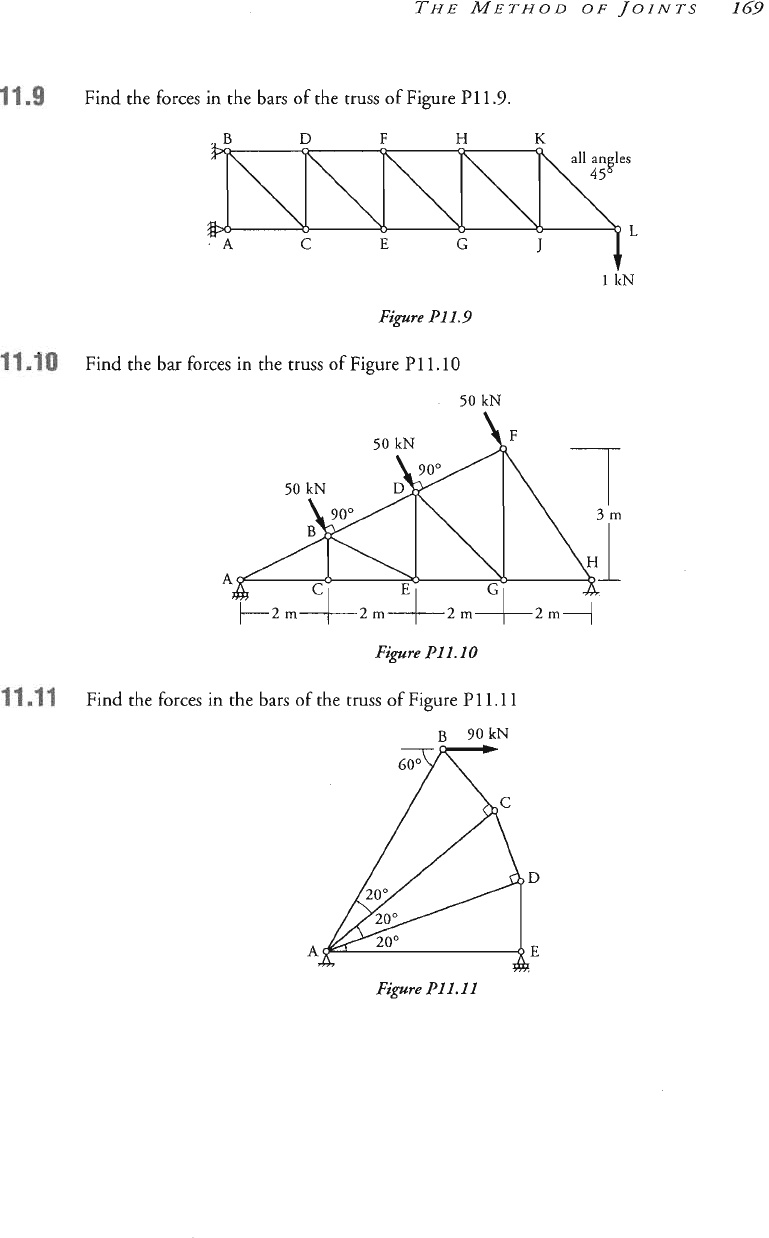
Find the forces in the bars of the truss of Fi
l
kN
Find the bar forces
in
the truss
of
Figure
P1
1.10
50
kN
A
Find the forces in the
bars
of
the
truss of Figure
P
1
1.1
1
B
90kN
