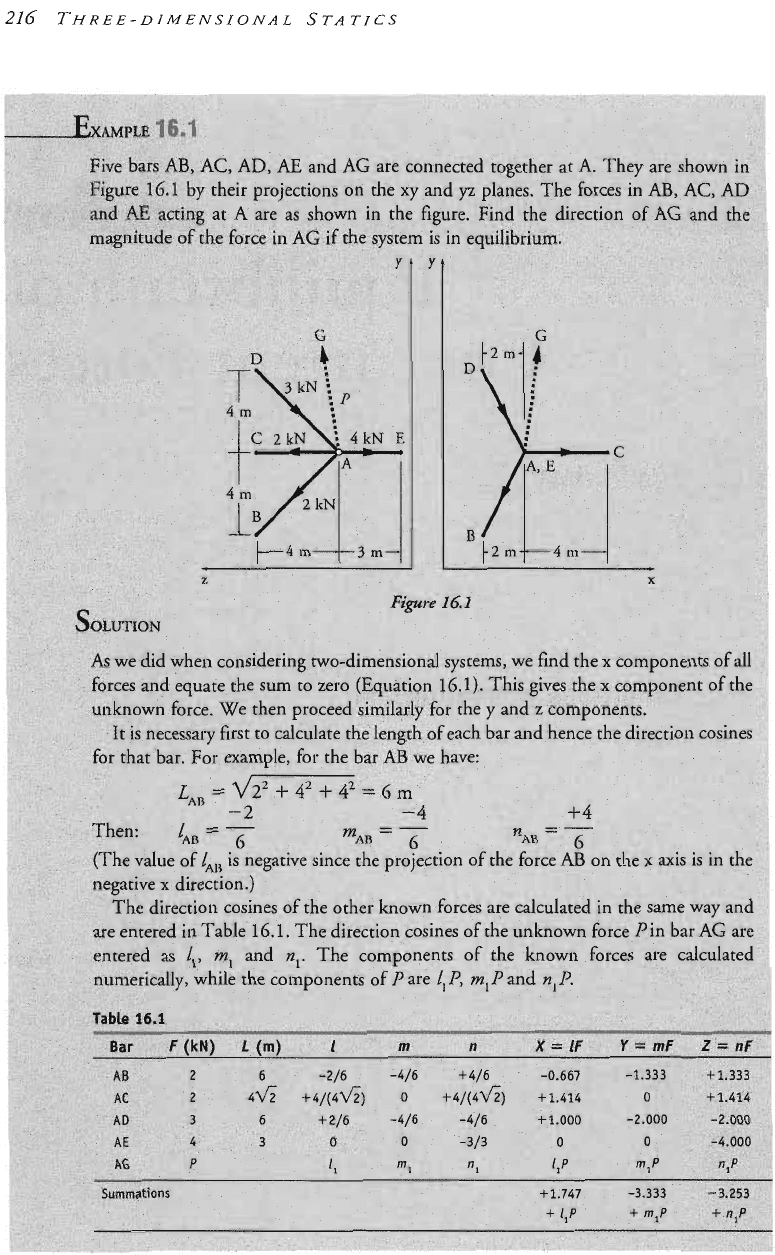
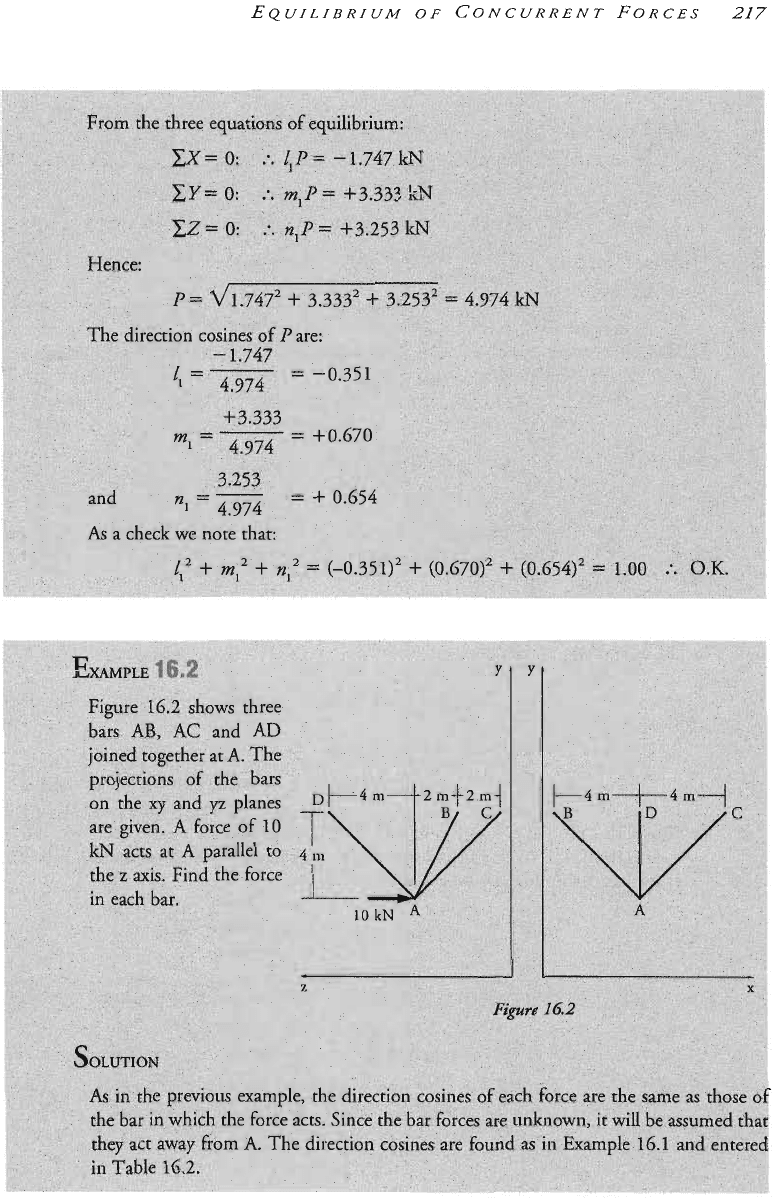
Hall A.S., Archer F.E., Gilbert R.I. Engineering Statics
Подождите немного. Документ загружается.


The methods used for the co~position ofcoIlcurrent coplanar forces can be extended to
deal with the composition of co~c~rrent forces
in
three di~ensions (i.e. forces which are
not nec~s~aril~ coplanar).
A
X
C

The sum
ofthe
co~ponenrs
in
the direction
Y=
q
+
y2
+
y3
+...+
y,
=
YK
the
sum of
the
~o~po~~nts
in the direct
e
the
~o~~onents
of
R,
the resu~t~nt
of
Fl, F,
. .
previous section
then, the
ma~nitu~e
of
the resultant
is:
4,
'F,,
+
2""F2
cos
a!
ilar ~~nne~, the student
may
prove
by
expan
use
of
the relationshi~s:
2+
$2,
=
l
and
cos

A
force of
90
N
acts along a line passing through the origin of co-ordinates
(0, 0,
0)
towards the point whose co-ordinates are
(4,
-4,
7).
Resolve this force into three
components along the x,
y
and
z
axes.
A
force Facts along a line passing through the origin
of
co-ordinates
(0,
0, 0)
towards a
point
A,
having co-ordinates
xl,
yI
and
zI,
Find the components along the
x,
y
and
z
axes
for each
of
the sets of values of
rl;
xl,
y1
and
zI
shown in Table
PI
5.2.
Table
P15.2
F
X,
V.
E.
0)
250
N
(ii)
180
N
(iii)
300
N
(iv)
520
N
(v)
280
N
3
6
-5
8
-2
4
l0
6 -6
9
12
3
-6
-5
4v%
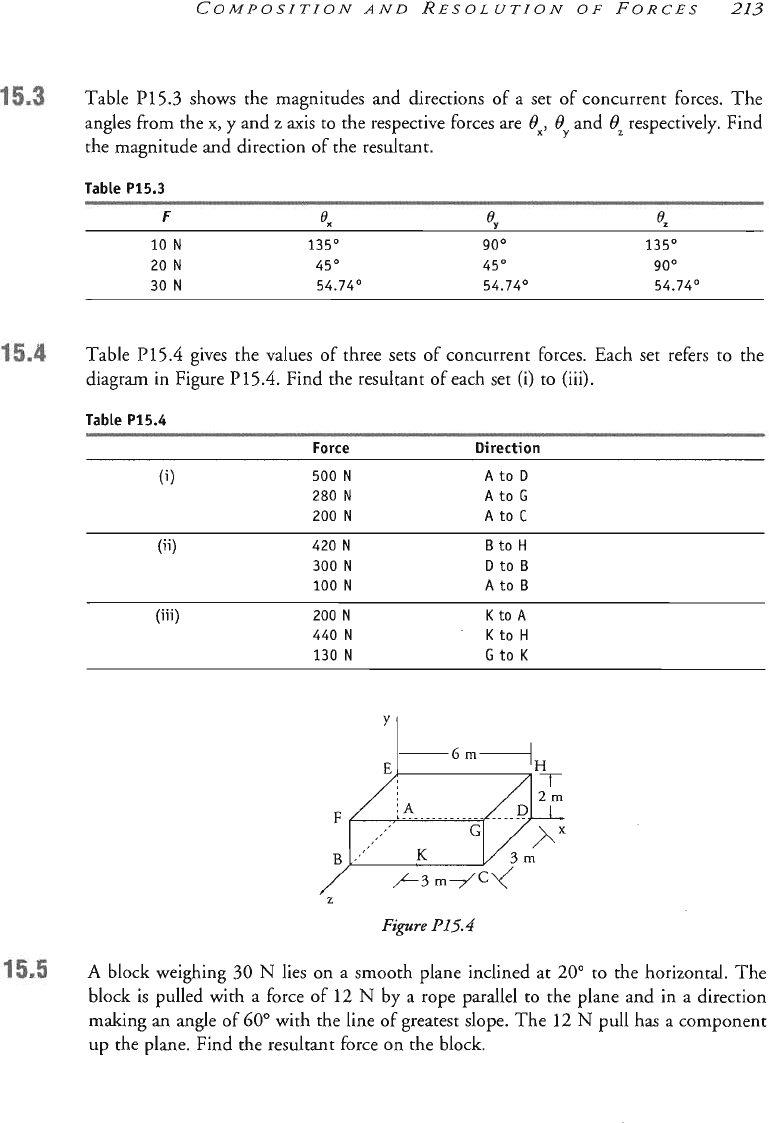
Table
PlS.3
shows the magnitudes and directions of
a
set of concurrent forces. The
om the
x,
y and z axis to the respective forces are
Ox,
By
and
Oz
respectively. Find
itude and direction of the resultant.
r?
%
c?
10
N
135'
goo
135'
20
N
45O 45O
goo
30
N
54.74O 54.74.O 54.74O
Table
PlS.4
gives the values of three sets of concurrent forces. Each set refers to the
diagram in Figure
P1
5.4.
Find the resultant of each set (i) to (iii).
arc irectio~
0)
500
N
280
N
200
N
A
to
D
A
to
G
A
to
C
(ii)
420
N
300
N
100
N
B
to
H
D
to
B
A
to
B
(iii)
200
N
440
N
130
N
K
to
A
K
to
H
G
to
K
A
block weighing
30
N
lies on
a
smooth plane inclined
at
20"
to the horizont~. The
block is pulled with a force of
12
N
by
a
rope parallel to the plane and in a direction
making an angle
of
60"
with the line of greatest slope. The
12
N
pull
has
a
component
up the plane. Find the resultant force on the block.


In Section
3.1,
it was shown that
as
a consequence of Newton’s Second Law, any body
at rest must be acted upon by a system of forces with a zero resultant. This
of
course
applies equally to three dimensional systems.
If
the resultant of a three di~ensional
system of concurrent forces
is
zero, the forces when added vectorially must form
a
closed
polygon in space (i.e. the last point of the force polygon must coincide with the
initial point).
The resultant of a system of concurrent forces has been shown to have three components
given by Equations
15.4.
That is:
If the resultant is zero, each
of
the components ust be zero. Hence,
the conditions of equilibrium are:
x=
0
I/=
0
z=
0
If a concurrent system of forces is known to be in equilibrium and
all
forces except
one are known in magnitude and direction, the above three equations may be used to
determine the un~own force in magnitude and direction. This problem is simply the
reverse of finding the resultant of the known forces.