Hall A.S., Archer F.E., Gilbert R.I. Engineering Statics
Подождите немного. Документ загружается.


In Section
4.3,
a
cu~~Ze
was
defined
as
a pair of parallel forces of equal magnitude but
opposite sense. The same applies to couples in a three dimensional system.
In
a
two-dimensional system, the only quantity which needed to be specified
was
the
~o~e~t
ufthe
cu~~Ze.
This
was
defined
as
the product of one of the forces and the
distance between them. In
a
thr~e-dimensional system it is necessa~ also to define the
ctzbn
ofthe
&xis
of rotation. This axis may be r&en
as
any line normal
to
the plane
h
contains the forces. The direction of such
a
normal is taken such that the couple
has
a
positive moment about the asis.
D
rotating the couple in its plane
I
transferring it to another position in its plane
The statical effect of a couple on
a
rigid body is unchanged by:
transferring the couple to
a
plane parallel to the original plane
product of the force and the distance remains constant.
ing the magnitude
of
the forces and distance between them, provided the
These properties are illustrated in Figure
17.4,
where
A
and
A'
are parallel planes and
LM
is
a
line normal to them. Each
of
the five couples shown has
a
magnitude
F&
and
each has an axis in the direction of
LM.

NON-CONCURRENT FORCES
232
A
couple, having magnitude and direction, is
a
vector quantity.
A
force, which requires
ma~nitude, direction and its line of action for its complete specification, is sometimes
called a
~uc~Zjse~
uecm+.
It is not necessary to specify the line of action in the case of
a
couple. It is ofien convenient to denote a couple by means of
a
double-headed arrow, the
length of which corresponds to the magnitude. In Figure
17.4,
any of the five couples
could be represented by the arrow at
L
or alternatively by the arrow at
N
as
shown.
Two couples may be replaced by
a
single couple which has the same statical effect
as
the
two
couples combined.
If the
two
couples lie in the same plane, or in parallel planes, then their ~agnitu~es
may simply be added algebraically, their directions being the same. This was the situation
dealt with in ~o-dimensional systems (Chapter
4).
If they do not lie in parallel planes
(i.e. if they do not have the same direction) an expression for their resultant may be
obtained from the work of earlier chapters,
as
follows.
Figure
17.5a
shows
a
couple consisting of
two
forces
P
lying
in
a
plane A. The
moment of this couple is
M'
=
Pe.
Another couple consists of
two
forces
plane
B
which is at an angle
a
to plane
A.
The moment of this couple is
MB
=
Qf
In
order to combine them, the couple of moment
MA
is replaced by
a
pair of forces
R
at
distance
LZ
apart in the plane
A,
such that one of the forces
R
acts along the line of
intersection
of
the
two
planes (line
IJ
in Figure
17.5a).
The couple of moment
M,
is
similarly replaced by an equivalent couple
Rb
in plane
B,
arranged
so
that one of the
forces
R
acts along IJ and opposes the force
R
from the couple
MA.
""""_
plane
A
"""
""""_
Pipre
IZ.5
Of
the four forces
R,
two
cancel out and the remaining
two
constitute
a
couple lying in
a plane oblique to
A
and
B.
To find the magnitude of this couple we need the distance
c
between the forces. Figure
17.5b
is
a
view looking directly along the line of intersection
of planes
A
and
B
(i.e. line IJ). It can be seen that:
c"
=
L?
+
b2
+
2abcos
cx
or
PC2
PL?
+
R2b2
+
2(&)
(Rb)
cos
a
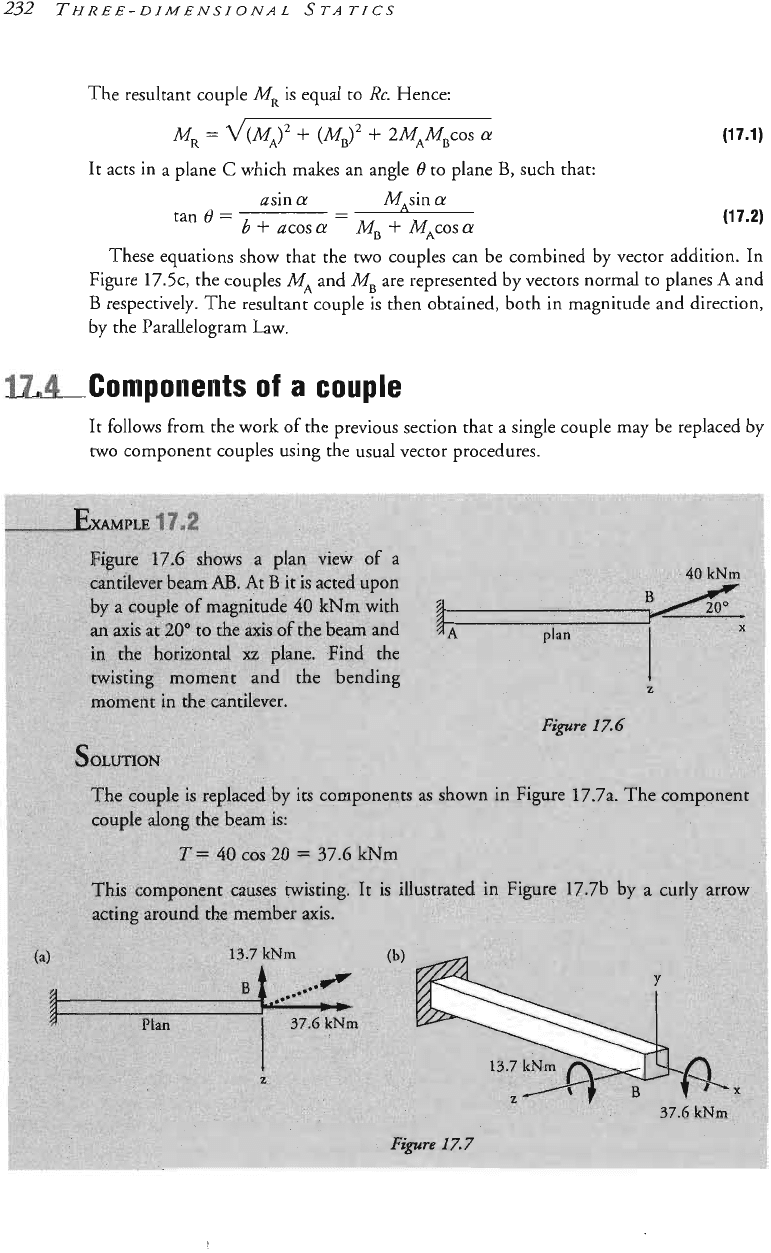
232
THREE-DIMENSIONAL
STATICS
The resultant couple
MR
is
equal to
RC.
Hence:
LWR
=
~("~)z
+
(~~)2
+
2"~M~COS
a
It acts in a plane
C
which makes an angle
6
to plane
asin
a
"'sin
a
b
+
COS
a
AdB
+
cos
a
tan
0
=
-
_I
3,
such that:
These equations show that the
two
couples can be combined by vector addition. In
Figure 17.5c, the couples
M,
and
MB
are represented by vectors normal to planes
A
and
€3
respectively. The resultant couple is then obtained, both in magnitude and direction,
by the Parallelogram Law.
It follows from the work of the previous section that a single couple may be replaced
by
two component couples using the
usual
vector procedures.

More generally, if a couple has a magnitude
IM
and its axis has direction cosines
I,
m
and n then it may be replaced by couples of magnitude
IM,
mIMand nMacti~
the axes
Ox,
Oy
and
Oz
respectively.
The resultant of a number of couples may be determined by first resolvin
into
its
components around the axes
x,
y
and
z.
If
the resultant couple
MR,
has
components,
Mk,
M&
and
M&
then:
and finally:
=
(yJ2
+
+
(MR~)2
For a two-dimensional system of forces, lying in the
xy
plane and concurrent at the point
A,
the resultant is the single force which has the same x component as the combined
forces and the same y component as the combined forces. The resultant also passes
through the point
A.
In Chapter
15,
we saw that this concept could readily be extended
to the three-dimensional situation merely by requiring that the resultant also has the
same z component as the combined forces. Again it passes through
A.
In Section
4.2,
the determination of the resultant of a two-dimensional system of
non-concurrent forces, such as that shown in Figure 17.9, was discussed. The
magnitude and direction of the resultant are found as for a concurrent system, but the
position also needs to be established. Provided the resultant force is non-zero, it can be
located so that its moment about any arbitrarily chosen point (say
B
in Figure
17.9)
is
the same
as
the combined moments of the force system. Fortunately, if
R
has the same
moment about an axis through
B
as do the original forces, then its moment about an
axis through any other point
C
will also be equal to that of the original forces.
Of
course, the various axes considered are
all
normal to the plane of the force system.
However, if the resultant force is zero, it is necessary to express the resultant as a couple,
unless the system is in equilibrium.

NON-CONCURRENT
FORCES
2.35
This concept of a single resultant force cannot be
extended to the case of a three-dimensional system of non-
conc~~rrent forces except in special cases. In three
dimensions it is possible to imagine the moment of a force
about axes in various directions. We may find the
magnitude and direction of
R
by the methods of Chapter
15.
By
moving
R
(but retaining the same direction) we
may cause
R
to have the same moment
as
the original forces
about any
two
axes (say
Ox
and
Oy).
But
R
is then
completely defined, and if its moment about
Oz
is not equal to that of the original forces,
then we cannot express the resultant as a single force. It must be accompanied by a
suitable couple.
In other words, we can replace a given system of forces by a statically equivalent
system, but this system cannot be a single force except in special cases.
In Section
4.5
we saw that a given system of forces in two-dimensions can be replaced
by another system provided that the new system contains three undeter~ined quantities.
These three quantities can be evaluated
so
that the new system
is
statically equivalent to
a three-dimensional system can be replaced by a statically equivalent
system provided the new system contains
six
undetermined quantities.
As
in the
two-
di~ension~ case there are certain restrictions on the choice of the undetermined quantities.
We consider first the problem of replaci any given force by three component forces
specified axes
Ox,
Oy
and together with three component couples
ote that in the new syste~ the directions and positions of six vectors
(three forces and three couples) are specified, but six ma~nitudes are undetermined.
These may then be determined to ensure equivalence.
2
iven force
F
act through the point
A
(x,?
yI,
zs)
in a direction such that the
sines are
(,ll,
m,,
n,)
as
shown in Figure
17.
loa. The force is first replaced by
its three orthogonal components at
A.
These are
ZIF,
m,Fand
n,F
(Fi
now
have to find a new system consisting of three forces
.X
Yand Zand three couples
Mx,
My
and
Mz
at the origin, which is statically equivalent to the system of Figure 17.10b.
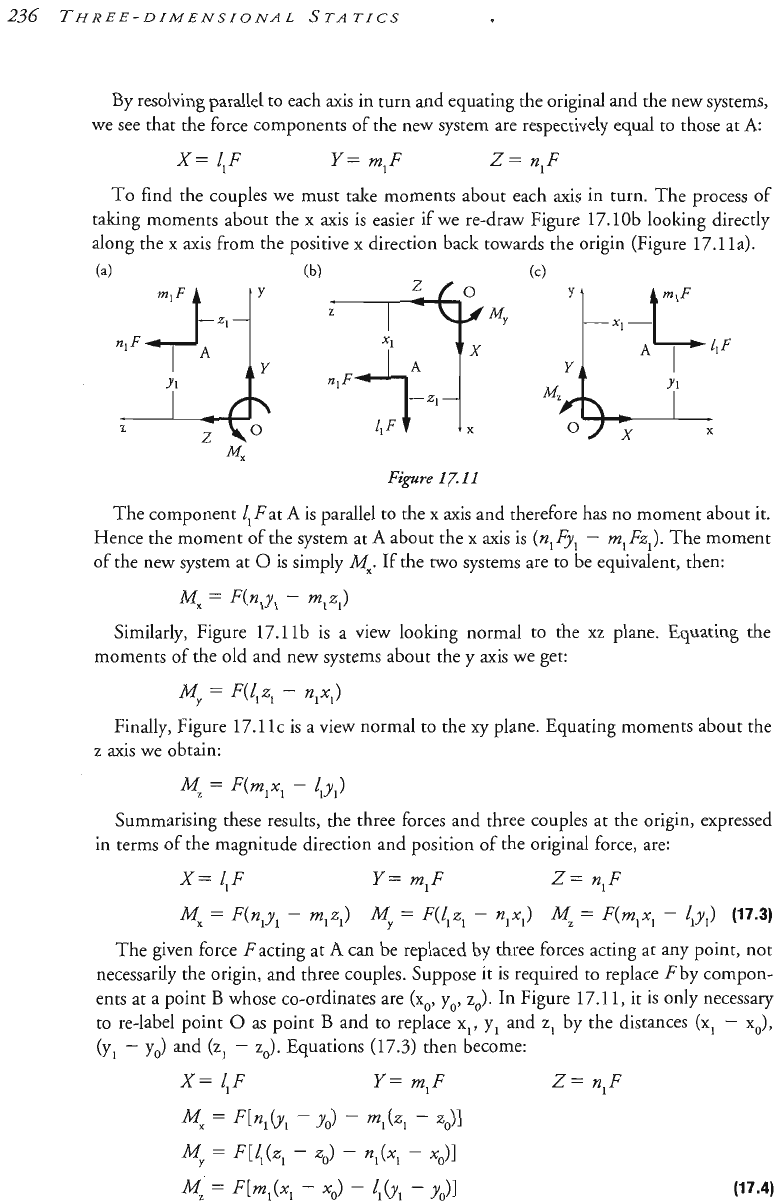
By resolving parallel to each axis in turn and equating the original
and
the new systel~s,
we see that the force components of the new system are respectively equal to those at
A:
To find the couples we must take moments about each axis in turn, The process of
taking ~oments about the
x
axis is easier if we re-draw Figure 17. lob looking directly
along the
x
axis from the positive
x
direction back towards the origin (Figure 17.
l
la),
The component 2,Fat
A
is parallel to the
x
axis and therefore has no moment about it.
Hence the moment of the system at
A
about the
x
axis is
(n,Fyl
-
m,Fz~).
The moment
of the new system at
Q
is simply
Mx.
If the
two
systems are to be equivalent, then:
Similarly, Figure 17.
l l
b is a view looking
normal
to the
xz
plane. Equatin
~o~ents of the
old
and new systems about the y axis we get:
My
=
F(Zlz,
-
n,x,)
Finally, Figure 17.
l
IC is a view normal to the
xy
plane. Equating moments about the
z
axis we obtain:
Summarising these results, the three forces and three couples at the ori
in terms of the magnitude direction and position
of
the original force, are:
X=
ZIF
Y=
m,F
Z=
n,F
The given force
F
acting at
A
can be replaced by three forces actin
necessarily the origin, and three couples. Suppose it is required to re
whose co-ordinates are
(x,,
yo,
2,).
En Figure
1’7.
l l,
it
is
only
le cess^^
to re-label point
Q
as
point
B
and
to
replace
xI,
y1 and
z1
by the distances
(x1
-
x,),
(y,
-
yo) and
(zl
-
2,).
Equations (17.3) then become:
X=
ZIF
Y=
mlF
=
n,
F

NON-CONCURRENT FORCES
237
The three component forces
x
Yand Zat
El
can be re-co
E
which will obviously be equal to
I;.
The three couples
Mx
combined into
a
single couple, the
axis
of which will not,
i
line of action of
E
It
has
therefore been shown that
a
force can be replaced by a parallel
force at any other point together with
a
couple. We note that this system again contains
six
quantities to be determined, namely a ma~nitude and
two
direction cosin
the force, and a magnitude and
two
direction cosines to define the couple,
It
is not necessary for the replacement system to comprise three concurren~
Component forces
and
three component couples, To be valid, the replacement system
must contain
six
inde~endent ulldetermined quantities. It must be capable of providing
a
force component in every direction and must have
a
moment about every
axis.
It
follows that at least three of the unknown quantities must be forces. Indeed, all
six
may
t
in such a case care must be taken to see that the system does have
a
t
every
axis
in space.
e
can say that any
two
systems are statically equivalent if both:
a
in each of three directions (not
all
in the same plane), the
sum
of the com~onents of
a
about any three
on-parallel
axes (not all in the same plane) the sum of the moments
one system
is
equal to the sum of the components of the other; and
of"
one system
is
equal to the sum of the moments of the other.

In
the foregoing problems, mo~ents have always been taken about axes parallel eirher
x,
Oy or
Oz.
In problems of this sort, even
if
the forces are oblique, it
is
a~~ro~riate
to resolve them into their
x,
y,
z
components before taking ~oments.
ccasionally it is necessary to take ~o~ents about an oblique axis.
To
deal with this
problem a more general approach to mo~ents
is
required.
An
expression
for
the ~omenr
of
a
force about
any
axis can be obtained
from
the results
of
Section 17.7.
In
Figure 17.13,
rhe force
F
acts through the point
A
(xi,
yl,
zi)
and has direction cosines
I,,
m,
an
while the
axis
S
passes through
B
(xo,
yo,
zo)
and
has
direction cosines
I,,
m.
and no.
The
force and the
axis
do
not intersect and are not parallel,
so
that Fhas a ~oment about
S.

We first replace
F
by a parallel force through
B
together with three component
couples. The new force has no ~oment about
S,
and the moment of the cou
readily obtained, From Equations
17.4,
the couple about the
x
axis is:
Mx
=
F[n,(y,
-
yo>
-
m,
(g1
n/ls
=
Mx~
=
F[n,(y,
-
yo>
-
ml(zl
-
41
l*
The component of this couple along axis the
mom en^
of this cou
The com~onen~s of the other couples
My
and
M'
are obtained
in
a similar way, and upon
This expression is convenientl~ iven in the form of a determinant:
