Haddad W.M. Nonlinear Dynamical Systems and Control: A Lyapunov-Based Approach

Подождите немного. Документ загружается.

NonlinearBook10pt November 20, 2007

ROBUST NONLINEAR CONTROL 695

LQR

Speyer

Robust LQR

Robust Nonlinear

0 1 2 3 4 5 6 7 8 9 10

-0.6

-0.4

-0.2

0.2

0.4

0.6

0.8

time (sec)

position of mass 1

Figure 11.6 Comparison of LQR, Speyer, robu st LQR, and robust nonlinear controllers

for the uncertain system: Position of mass 1.

Theorem 11.6. Consider the linear uncertain controlled system

˙x(t) = (A + ∆A)x(t) + Bu, x(0) = x

, t ≥ 0, (11.200)

where u(·) ∈ U is admissible and ∆A ∈ ∆

. Assume there exist Ω : N

→

, P ∈ P

Ω

: N

(2ν,n)

→ N

(2ν,n)

, and

∈ N

(2ν,n)

, ν = 2, . . . , r, such

that

∆A

P + P ∆A ≤ Ω(P ), ∆A ∈ ∆

, (11.201)

Ω

(

) −

(

2ν

⊕ ∆A) ∈ N

(2ν,n)

, ∆A ∈ ∆

, ν = 2, . . . , r, (11.202)

0 = A

P + P A + R

− P SP + Ω(P ), (11.203)

and

0 =

[

2ν

⊕ (A −SP )] +

2ν

Ω

(

), ν = 2, . . . , r. (11.204)

Then, with the feedback control u = φ(x) = −R

−1

(P x +

′

(x)), where

g(x)

△

ν=2

[2ν]

, th e zero solution x(t) ≡ 0 of the uncertain system

(11.200) is globally asymptotically stable for all x

∈ R

and ∆A ∈ ∆

and the performan ce functional (11.127) satisﬁes

sup

∆A∈∆

∆A

, φ(x(·))) ≤ J(x

, φ(x(·))) = x

P x

ν=2

[2ν]

, (11.205)

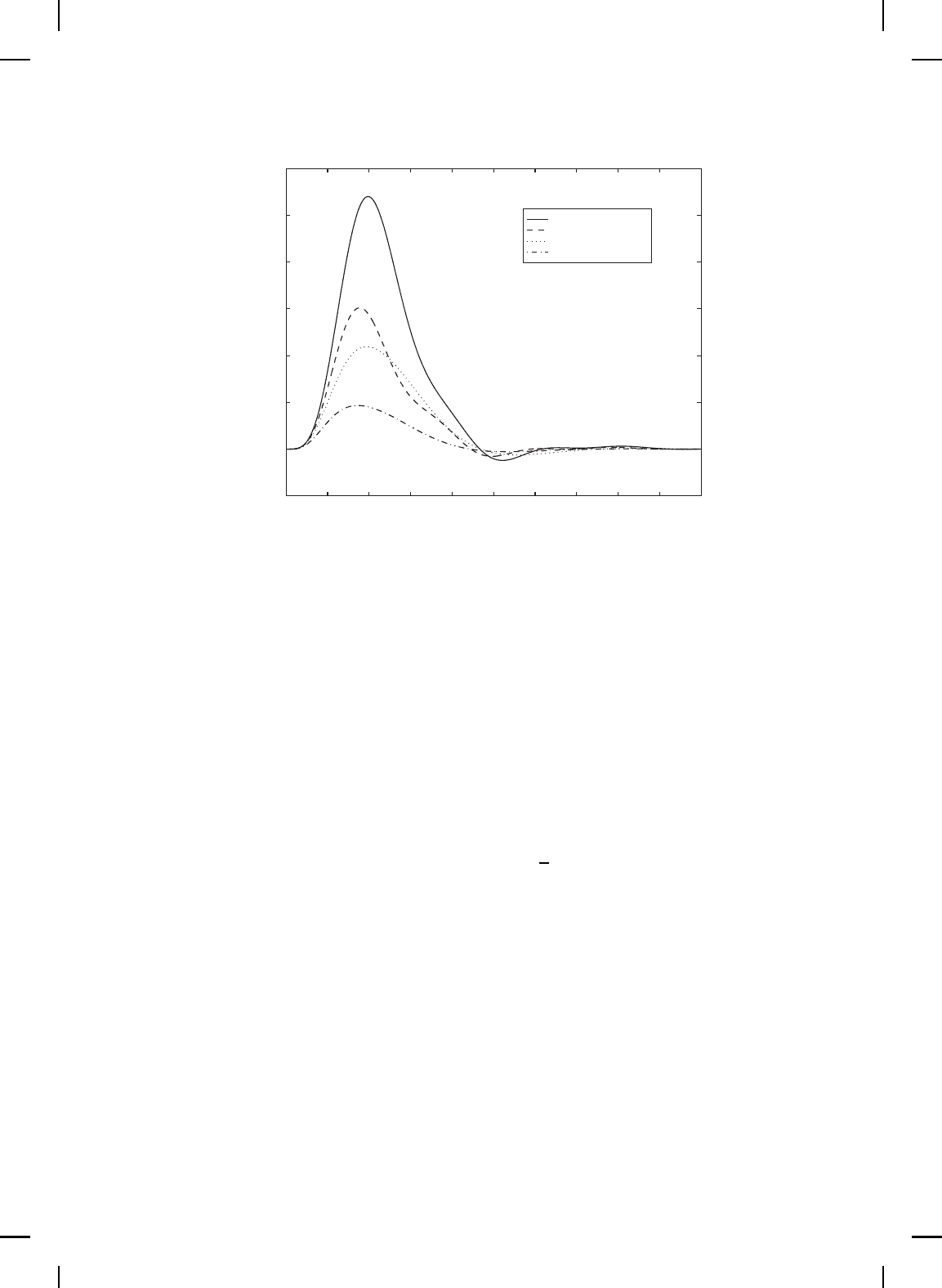
NonlinearBook10pt November 20, 2007

696 CHAPTER 11

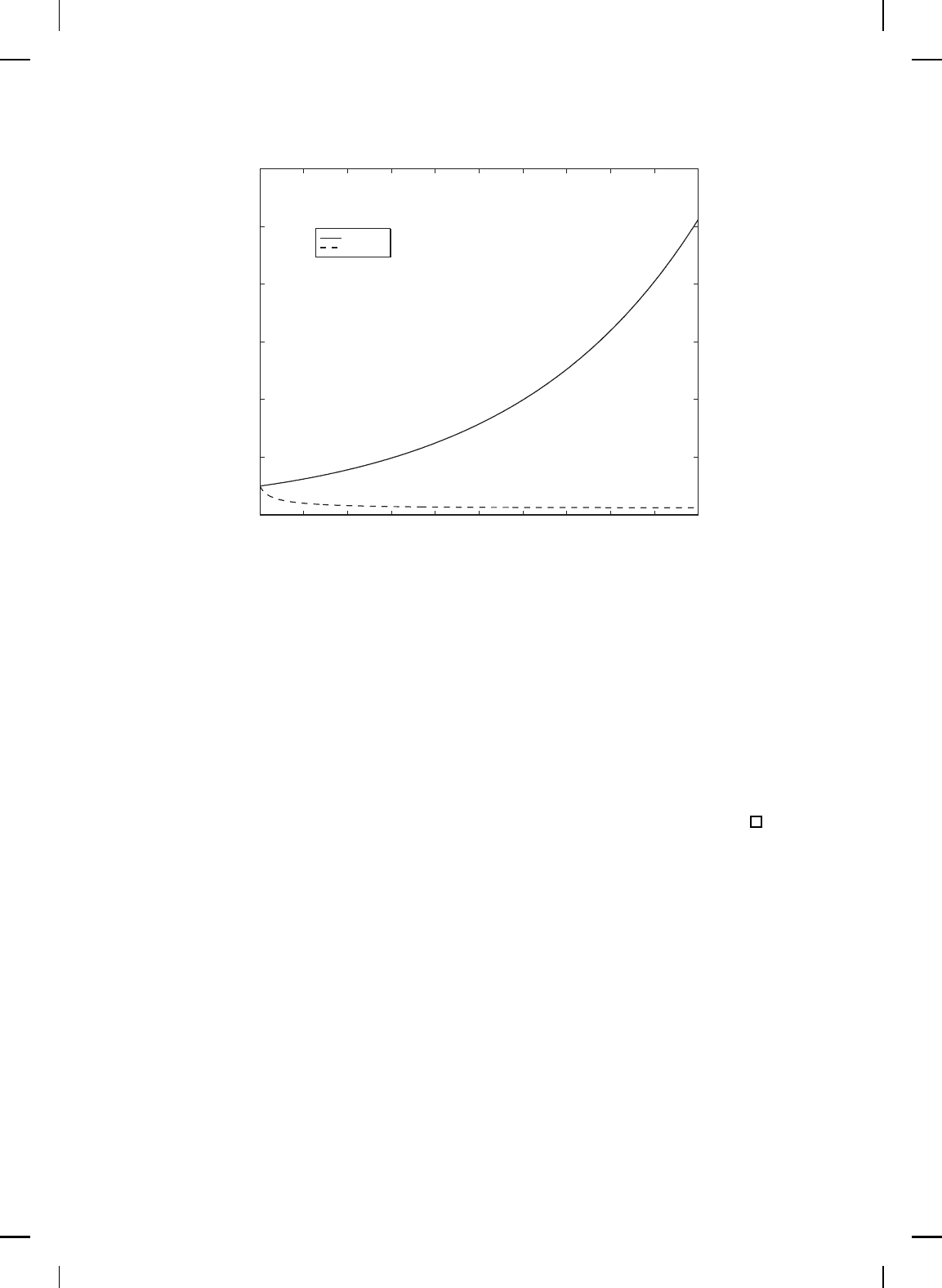
LQR

Speyer

Robust LQR

Robust Nonlinear

0 1 2 3 4 5 6 7 8 9 10

-0.02

0.02

0.04

0.06

0.08

0.1

0.12

time (sec)

position of mass 3

Figure 11.7 Comparison of LQR, Speyer, robu st LQR, and robust nonlinear controllers

for the uncertain system: Position of mass 3.

where

J(x

, u(·))

△

∞

[L(x, u) + Γ(x, u)]dt, (11.206)

and where u(·) is admissible, and x(t), t ≥ 0, solves (11.200) with ∆A = 0

and

Γ(x, u) = x

Ω(P )x +

ν=2

Ω

(

[2ν]

where u(·) is admissible and ∆A ∈ ∆

. In addition, the performance

functional (11.127), with R

(x) = R

, L

(x) = 0, and

(x) = x

x +

ν=2

2ν

[2ν]

′

(x)Sg

′

(x)

is minimized in the sense that

J(x

, φ(x(·))) = min

u(·)∈S(x

)

J(x

, u(·)), (11.207)

where S(x

) is the set of regulation controllers for the nominal system and

∈ R

Proof. The result is a direct consequence of Corollary 11.4 with

(x) = Ax, G

(x) = B, ∆f(x) = ∆Ax, ∆G(x) = 0, ∆

= ∆

, and

V (x) = x

P x +

ν=2

[2ν]

. Speciﬁcally, conditions (11.128)–(11.162) are

NonlinearBook10pt November 20, 2007

ROBUST NONLINEAR CONTROL 697

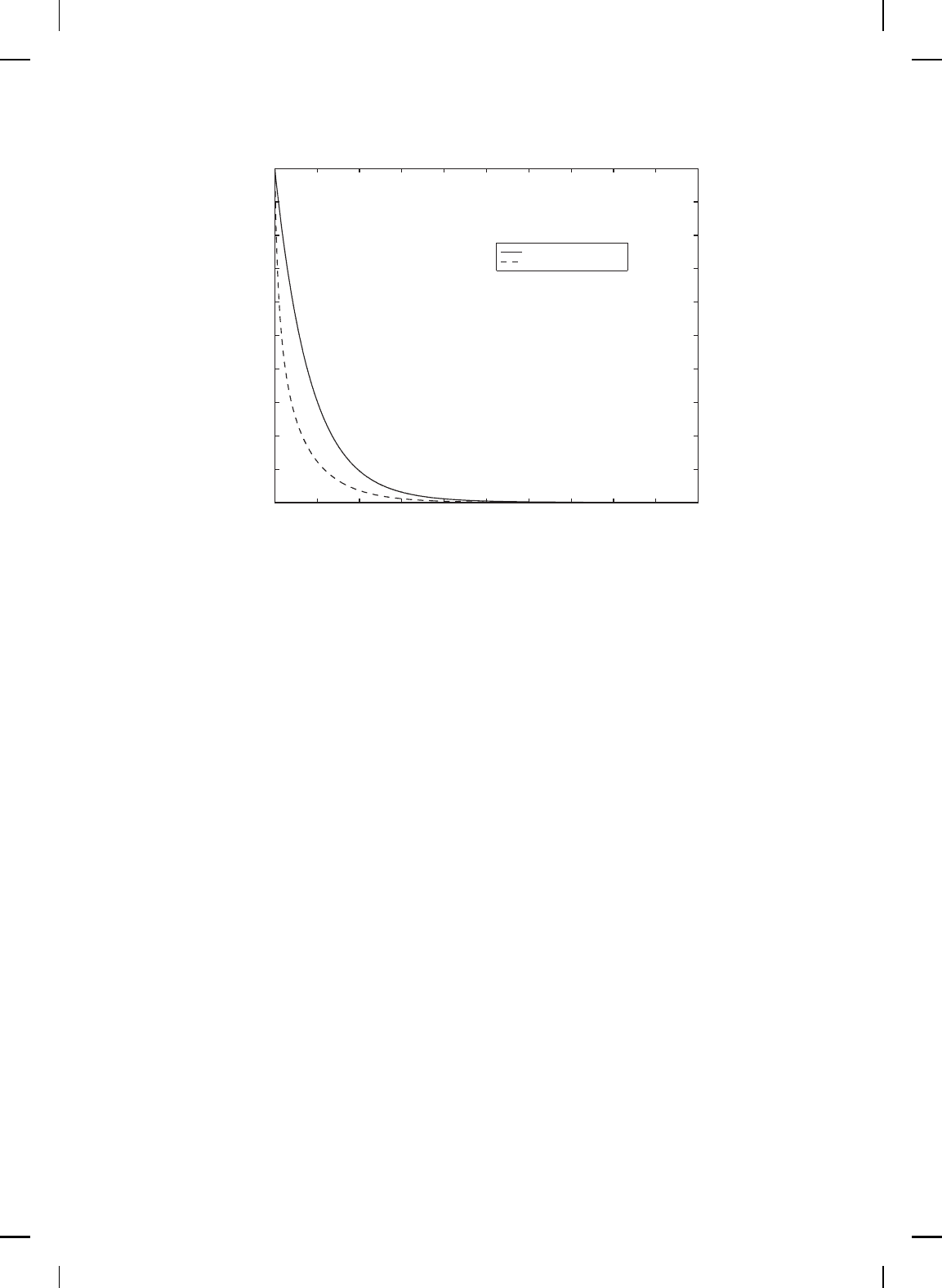
LQR

Speyer

0 0.5 1 1.5 2 2.5 3 3.5 4 4.5 5

time (sec)

angle of attack (rad)

Figure 11.8 Comparison of LQR and Speyer controllers for the uncertain system: Angle

of attack.

trivially satisﬁed. Now, it follows from (11.201) and (11.202) that

(∆A

P + P ∆A − Ω (P ))x +

ν=2

[

(

2ν

⊕ ∆A) −

Ω

(

)]x

[2ν]

≤ 0, x ∈ R

which implies (11.133) for all ∆A ∈ ∆

so that all the conditions of

Corollary 11.4 are satisﬁed.

Note that since g

′

(x)(A−SP )x =

ν=2

[

2ν

⊕ (A −SP )]x

[2ν]

it follows

that (11.204) can be equivalently written as

0 = g

′

(x)(A − SP )x +

ν=2

[

2ν

Ω

(

)]x

[2ν]

for all x ∈ R

, and hence, it follows from Lemma 8.1 that there exists a

unique

∈ N

(2ν,n)

such that (11.204) is satisﬁed. Theorem 11.6 generalizes

the classical resu lts of Bass and Webber [33] to robust nonlinear optimal

control.

NonlinearBook10pt November 20, 2007

698 CHAPTER 11

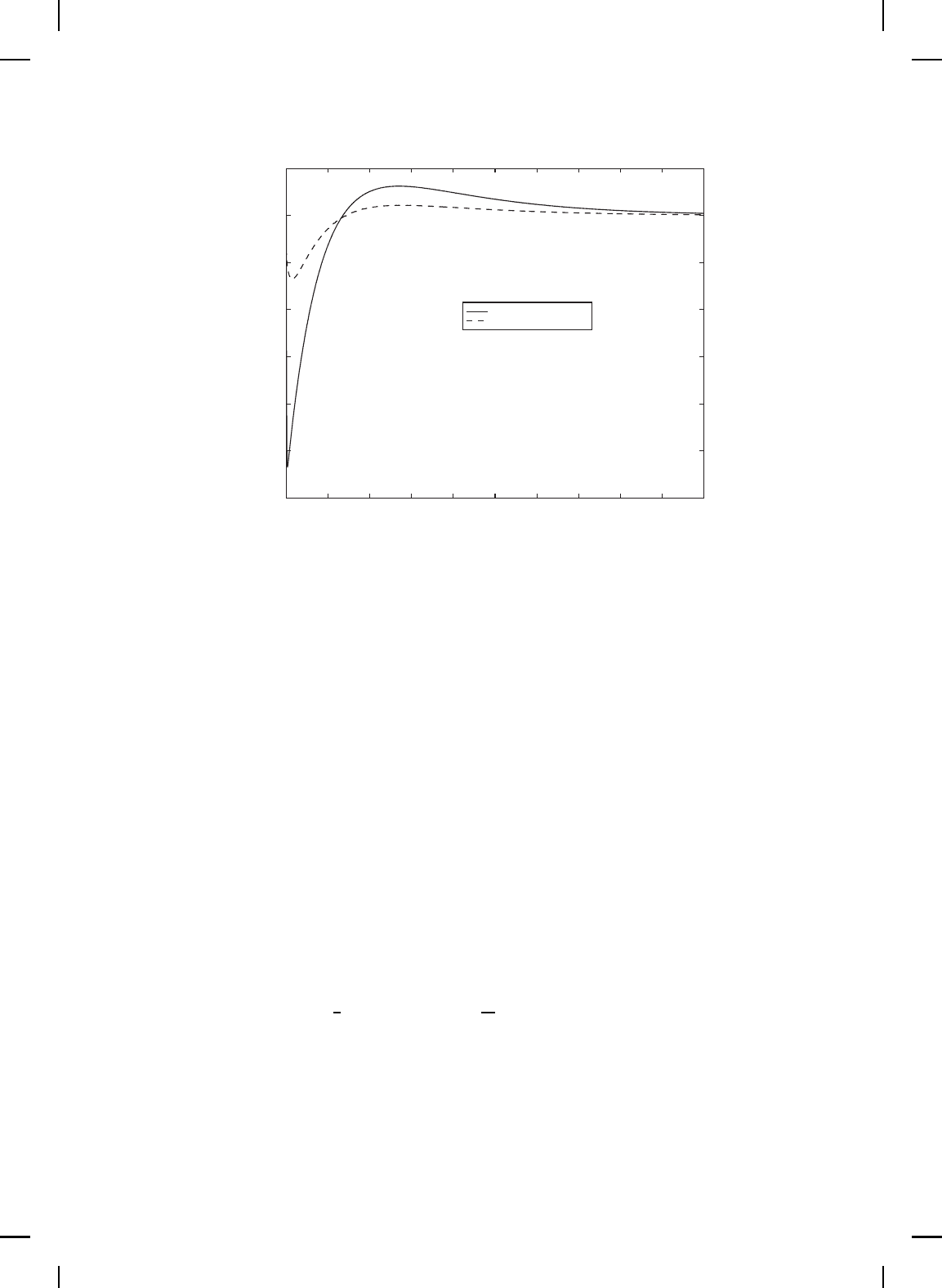
LQR

Speyer

0 0.5 1 1.5 2 2.5 3 3.5 4 4.5 5

-0.25

-0.2

-0.15

-0.1

-0.05

0.05

time (sec)

pitch rate

Figure 11.9 Comparison of LQR and Speyer controllers for the uncertain system: Pitch

rate.

11.10 Problems

Problem 11.1. Consider the linear oscillator

¨q(t) + 2ζω

˙q(t) + ω

q(t) = 0, q(0) = q

, ˙q(0) = ˙q

, t ≥ 0, (11.208)

where q, ˙q, ¨q ∈ R, and ζ ∈ [ζ

, ζ

] and ω

denote the damping ratio and

natural frequency, respectively, with ζ

and ζ

denoting the lower and upper

bounds on ζ. Using x(t) = [q(t), ˙q(t)]

, represent (11.208) as (11.50) with

∆

given by (11.56).

Problem 11.2. Consider the linear matrix second-order uncertain

dynamical system given by

M ¨q(t) + (C

+ ∆C) ˙q(t) + (K

+ ∆K)q(t) = 0, q(0) = q

, ˙q(0) = ˙q

, t ≥ 0,

(11.209)

where q, ˙q, ¨q ∈ R

, M

, C

, and K

denote generalized inertia, damping,

and stiﬀness matrices, respectively, and ∆C and ∆K denote damping and

stiﬀness uncertainty such that σ

max

(∆C) ≤ γ

−1

and σ

max

(∆K) ≤ γ

−1

Using x(t) = [q(t), ˙q(t)]

, represent (11.209) as (11.50) with ∆

given by

(11.27).

NonlinearBook10pt November 20, 2007

ROBUST NONLINEAR CONTROL 699

Robust LQR

Robust Nonlinear

0 0.5 1 1.5 2 2.5 3 3.5 4 4.5 5

0.05

0.1

0.15

0.2

0.25

0.3

0.35

0.4

0.45

0.5

time (sec)

angle of attack (rad)

Figure 11.10 Comparison of robust LQR and robust nonlinear controllers for the

uncertain system: Angle of attack.

Problem 11.3. Consider the uncertainty characterizations

∆

△

= {∆A ∈ R

n×n

: ∆A =

i=1

, |δ

| ≤ γ, i = 1, . . . , p}, (11.210)

∆

△

= {∆A ∈ R

n×n

: ∆A = B

F C

, σ

max

(F ) ≤ γ}, (11.211)

where for i = 1, . . . , p, A

∈ R

n×n

, B

∈ R

n×s

, and C

∈ R

s×n

are given, and

γ > 0. Show that ∆

is equivalent to ∆

in the sense that an uncertainty

set ∆

can always be written in the f orm of ∆

and vice versa.

Problem 11.4. Consider the linear uncertain system (11.50) where

∆A ∈ ∆

and ∆

is given by

∆

△

= {∆A ∈ R

n×n

: ∆ A =

i=1

, |δ

| ≤ γ

, i = 1, . . . , p}. (11.212)

Show that th e function

Ω(P ) =

i=1

P + P A

|, (11.213)

where |S| denotes (S

)

1/2

for S ∈ S

and (·)

1/2

denotes the (unique)

nonnegative-deﬁnite square root, satisﬁes (11.52) with ∆

given by (11.212).

NonlinearBook10pt November 20, 2007

700 CHAPTER 11

Robust LQR

Robust Nonlinear

0 0.5 1 1.5 2 2.5 3 3.5 4 4.5 5

-0.12

-0.1

-0.08

-0.06

-0.04

-0.02

0.02

time (sec)

pitch rate

Figure 11.11 Comparison of robust LQR and robust nonlinear controllers for the

uncertain system: Pitch rate.

Problem 11.5. Let f : R → R and deﬁne (with a minor abuse of

notation) f : S

→ S

by f (S)

△

= Uf(D)U

, where S = UDU

, U is

orthogonal, D is real diagonal, and f (D) is the diagonal matrix obtained

by applying f to each diagonal entry of D . Consider the linear uncertain

system (11.50) where ∆ A ∈ ∆

and ∆

is given by (11.212). L et f

: R →

R, i = 1, . . . , p, be such that f

(x) ≥ |x|, x ∈ R. Show that the function

Ω(P ) =

i=1

P + P A

) (11.214)

is an overbound for Ω(·) given by (11.213) and, hen ce, satisﬁes (11.52) with

∆

given by (11.212). (Hint: Note if f (x) = |x|, then f (S) = (S

)

1/2

where (·)

1/2

denotes the (unique) nonnegative-deﬁnite square root.)

Problem 11.6. Consider the linear uncertain system (11.50) where

∆A ∈ ∆

and ∆

is given by (11.212). Let β

, . . . , β

be arbitrary positive

constants. Show that the function

Ω(P ) =

i=1

(

)(A

P + P A

)

(11.215)

is an overbound for Ω(·) given by (11.213) and, hen ce, satisﬁes (11.52) with

∆

given by (11.212).

NonlinearBook10pt November 20, 2007

ROBUST NONLINEAR CONTROL 701

Problem 11.7. Let ∆

given by (11.212) be deﬁned by the positive

constants γ

, . . . , γ

and let ∆

given by (11.56) be characterized by α



αγ



1/2

, i = 1, . . . , p, where α

△

i=1

and β

, . . . , β

are arbitrary

positive constants. Sh ow that the ellipse E

△

= {(δ

, . . . , δ

) :

i=1

≤ 1}

circumscribes the rectangle R

△

= {(δ

, . . . , δ

) : |δ

| ≤ γ

, i = 1, . . . , p}, and

hence, ∆

given by (11.56) contains ∆

given by (11.212).

Problem 11.8. Consider the linear uncertain system (11.50) where

∆A ∈ ∆

and ∆

is given by (11.56). Let α be an arbitrary positive

constant. Show that the function

Ω(P ) =

+ α

−1

i=1

P + P A

)

(11.216)

satisﬁes (11.52) with ∆

given by (11.56).

Problem 11.9. Consider the linear uncertain system (11.50) where

∆A ∈ ∆

and ∆

is given by (11.56). Let α be an arbitrary positive

constant. Show that for P > 0 th e function

Ω(P ) =

P +

−1

i=1

P + A

P A

+ P A

−1

P + P A

] (11.217)

satisﬁes (11.52) with ∆

given by (11.56).

Problem 11.10. Consider the linear uncertain system (11.50) where

∆A ∈ ∆

and ∆

is given by

∆

△

= {∆A ∈ R

n×n

: ∆A =

i=1

, |δ

| ≤ γ

−1

, i = 1, . . . , p}, (11.218)

where γ > 0. For i = 1, . . . , p, let α

∈ R, β

> 0, S

∈ R

n×n

and deﬁne

△

= [(S

+ S

)

]

1/2

and

△

= [S

][S

]

†

. Show that th e function

Ω(P ) =

i=1

[γ

−2

(α

+ β

P )

(α

+ β

P ) + γ

−1

|α

+ β

(11.219)

satisﬁes (11.52) with ∆

given by (11.218). (Hint: First show that

= S

, and A

= A

Problem 11.11. Consider the linear uncertain system (11.50) where

∆A ∈ ∆

and ∆

is given by (11.56). Let α be an arbitrary positive

constant and for each P ∈ P

, let P

∈ R

n×m

and P

∈ R

m×n

satisfy

NonlinearBook10pt November 20, 2007

702 CHAPTER 11

P = P

. Show that the function

Ω(P )

△

= αP

+ α

−1

i=1

(11.220)

satisﬁes (11.52) with ∆

given by (11.56). Using (11.220) show that the

functions

Ω(P )

△

= αI

+ α

−1

i=1

(11.221)

and

Ω(P )

△

= αP

+ α

−1

i=1

, (11.222)

also satisfy (11.52) with ∆

given by (11.56).

Problem 11.12. Consider the linear uncertain system (11.50) where

∆A ∈ ∆

and ∆

is given by (11.210). Let α > 0, N

∈ S

, i = 1, . . . , p,

and deﬁne N

△

= {P ∈ P

: P − N

≥ 0, i = 1, . . . , p}. Show that the

function

Ω(P ) =

i=1

[α(P − N

) +

(P − N

+ γ|A

+ N

|], (11.223)

where |S| denotes (S

)

1/2

, satisﬁes (11.52) with ∆ given by (11.210).

Problem 11.13. Consider the linear uncertain system (11.50) where

∆A ∈ ∆

and ∆

is given by (11.210). Let α > 0, V

, V

∈ R

n×n

, N

∈ S

i = 1, . . . , p, and deﬁne N

△

= {P ∈ P

: (P − N

) > 0}, i = 1, . . . , p. Show

that the function

Ω(P ) =

i=1

[α(P − N

) +

+ V

) + (V

+ V

4α

(P − V

) + (P − V

](P − N

)

−1

·[A

(P − V

) + (P − V

]

, (11.224)

where |S| denotes (S

)

1/2

, satisﬁes (11.52) with ∆

given by (11.210).

Problem 11.14. Consider the linear uncertain system (11.50) where

∆A ∈ ∆

and ∆

is given by (11.59). Show that if there exists P ∈ P

satisfying

0 = A

P + P A + γ

−2

P B

P + C

+ R, (11.225)

where γ > 0 and R > 0, then A + ∆A is asymptotically stable for all

∆A ∈ ∆

. Furthermore, show that there exists P ∈ P

satisfying (11.225)

if and only if |||C

(sI − A)

−1

|||

∞

< γ.

NonlinearBook10pt November 20, 2007

ROBUST NONLINEAR CONTROL 703

Problem 11.15. Consider the linear uncertain controlled system

(11.109) with ∆ B = 0, ∆A ∈ ∆

, where ∆

is given by (11.218), and

performance fun ctional (11.110). For i = 1, . . . , p, let α

∈ R, β

> 0,

∈ R

n×n

and deﬁ ne Z

△

= [(S

+ S

)

]

1/2

and

△

= [S

][S

]

†

. Show

that the zero solution x(t) ≡ 0 to (11.109) is globally asymptotically stable

for all ∆A ∈ ∆

with the feedback control φ(x) = −R

−1

P x, where

P > 0 satisﬁes

0 = A

sγ

P + P A

sγ

+ R

i=1

[γ

−2

(α

+ β

P A

P ) + γ

−1

|α

+β

] −P BR

−1

P, (11.226)

and A

sγ

△

= A + γ

i=1

Problem 11.16. Show that if R ∈ P

and

△

= A

⊕ A

i=1

⊗ A

is Hurwitz, then there exists a unique P ∈ R

n×n

satisfying (11.64) and

P > 0. Conversely, show that if for all R ∈ P

there exists P > 0 satisfying

(11.64), then A, A

, and A are Hur witz. (Hint: Use the exponential product

formula e

= lim

k→∞

{exp[

⊕ A

)t]exp[

i=1

⊗ A

)]}.)

Problem 11.17. Let ∆

be given by (11.56) and let

∆

⊆ ∆

, where

∆

is deﬁned as in (11.56) with α

replaced by ˆα

∈ [0, α

], i = 1, . . . , p.

Furth ermore, let R ∈ P

, assume A

△

= A

⊕A

i=1

⊗A

is Hurwitz,

and let P ∈ P

satisfy (11.64). Show that there exists

P ∈ P

satisfying

0 = A

P +

P A

+ α

−1

i=1

ˆα

P A

+ R, (11.227)

and

P ≤ P .

Problem 11.18. Show that if



(A ⊕A)

−1

αI

+ α

−1

i=1

⊗ A



< 1, (11.228)

where k·k den otes an arbitrary submultiplicative norm on R

, then for all

R ∈ P

there exists P ∈ P

satisfying (11.64).

Problem 11.19. Let κ, β > 0 satisfy ke

k ≤ κe

−βt

, t ≥ 0, where

A is Hurwitz and k · k denotes an arb itrary submultiplicative norm that is

monotonic on N

. Show that if R ∈ P

and 4αkB

k kα

−1

+Rk <

NonlinearBook10pt November 20, 2007

704 CHAPTER 11

, where ρ

△

= 2β/κ, then there exists P ∈ P

satisfying (11.68).

Problem 11.20. Consider the linear uncertain system (11.50) where

∆A ∈ ∆

and ∆

is given by

∆

△

= {∆A ∈ R

n×n

: ∆A = B

F C

, F ∈ ∆

}, (11.229)

where ∆

denotes the set of block-diagonal matrices with possibly repeated

blocks deﬁned by

∆

△

= {F ∈ R

s×s

: F = block−diag[I

⊗ F

, I

⊗ F

, . . . , I

⊗F

∈ R

×s

, i = 1, . . . , p}, (11.230)

and the dimen sion s

of each block and the number of repetitions l

of each

block are given such that

i=1

= s. Furthermore, deﬁne the s et of

constant scaling matrices D by

△

= {D ∈ R

s×s

: D > 0, DF = F D, F ∈ ∆

}. (11.231)

Show that if there exists P ∈ P

satisfying

0 = A

P + P A + γ

−2

P B

−2

P + C

+ R, (11.232)

where γ > 0 and R > 0, then A + ∆A is asymptotically stable for all

∆A ∈ ∆

△

= {F ∈ ∆

: σ

max

(F ) ≤ γ

−1

}. Furthermore, show that there

exists P ∈ P

satisfying (11.232) if and only if |||DG(s)D

−1

|||

∞

< γ, where

G(s) = C

(sI − A)

−1

Problem 11.21. Consider the linear uncertain system (11.50) and

(11.51) with n = 2,

A =



−ν ω

−ω −ν



, ν > 0, ω ≥ 0, (11.233)

V = E[x

] = I

, R = I

, and ∆A = {∆A : ∆A = δ

, |δ

| ≤ α

where



0 1

−1 0



. (11.234)

Show that (11.53) with Ω(P ) given by (11.213) or (11.219) is nonconservative

with respect to robust stability and performan ce. Alternatively, show that

(11.213) and (11.217) give extremely conservative predictions, especially

when ν is small.

Problem 11.22. Consider the linear dynamical system with state

delay given by

˙x(t) = Ax(t) + A

x(t −τ

), x(θ) = φ(θ), −τ

≤ θ ≤ 0, (11.235)

where x(t) ∈ R

, A, A

∈ R

n×n

, and φ : [−τ

, 0] → R

is a continuous

vector-valued fun ction specifying the initial state of the system. Show that