Haddad W.M. Nonlinear Dynamical Systems and Control: A Lyapunov-Based Approach
Подождите немного. Документ загружается.


NonlinearBook10pt November 20, 2007
ROBUST NONLINEAR CONTROL 665
= sup
∆A∈∆
A
E
Z
T
0
x
T
0
e
(A+∆A)
T
t
Re
(A+∆A)t
x
0
dt
= sup
∆A∈∆
A
E[x
T
0
P
∆A
x
0
]
= sup
∆A∈∆
A
tr P
∆A
V, (11.70)
where
0 = (A + ∆A)
T
P
∆A
+ P
∆A
(A + ∆A) + R (11.71)
and V = E[x
0
x
T
0
]. Now, since A is asymptotically stable,
E[J(x
0
)] = E
Z
∞
0
x
T
(t)(Ω(P ) + R)x(t)dt
= E
Z
∞
0
x
T
0
e
A
T
t
(Ω(P ) + R)e
At
x
0
dt
= E[x
T
0
P x
0
]
= tr P V, (11.72)
where P satisfies (11.53). Hence, it follows from (11.54) that J(x
0
), x
0
∈ R
n
,
provides an upper bound to the worst case, over the uncertainty s et ∆
A
, of
the H
2
norm of
G
∆A
(s) ∼
A + ∆A x
0
E 0
,
where E is such that R = E
T
E.
Example 11.5. Consider the linear uncertain dynamical system given
by (11.50) and (11.51) with n = 1, A < 0, R > 0, V = E[x
2
0
] > 0, A
1
= 1,
and ∆
A
= {∆A : |∆A| ≤ α
1
}. Note that for α
1
< − A, P
∆A
= R/2(|A| −
∆A) and J
∆A
(x
0
) = Rx
2
0
/2(|A|−α
1
), where this worst-case performance is
achieved for ∆ A = α
1
. Solving (11.64) with α = α
1
yields P = R/2(|A| −
α
1
), which is a nonconservative result for both robust stability and robust
performance. To apply (11.66), set α
1
=
√
N and B
0
= C
0
= 1. Choosing
α = 2α
1
(|A|−α)NR again yields the nonconservative result P = R/2(|A|−
α
1
). △
Example 11.6. Consider the linear uncertain dynamical system given
by (11.50) and (11.51) with n = 2, A = −I
2
, R = I
2
, V = E[x
0
x
T
0
] = I
2
,
and ∆
A
= {∆A : ∆A = δ
1
A
1
, |δ
1
| ≤ α
1
}, where
A
1
=
0 1
0 0
. (11.73)
Clearly, this perturbation is a nondestabilizing perturbation since A + ∆A
remains asymptotically stable for all values of δ
1
since ∆A does not affect

NonlinearBook10pt November 20, 2007
666 CHAPTER 11
the nominal poles. Furth ermore, note that
P
∆A
=
"
1
2
δ
1
4
δ
1
4
δ
2
1
4
+
1
2
#
(11.74)
and E[J
∆A
(x
0
)] =
1
4
α
2
1
+ 1, where this worst case is achieved for δ
1
= α
1
. In
this case, (11.64) has the solution
P =
(2 − αα
1
)
−1
0
0 (2 −αα
1
)
−1
+ α
−1
α
1
(2 − αα
1
)
−2
, (11.75)
which is positive defin ite for all α
1
so long as α < 2/α
1
. Hence, (11.64) is
nonconservative with respect to robust stability. For robust performance,
E[J(x
0
)] = tr P V = 2(2 −αα
1
)
−1
+ α
−1
α
1
(2 − αα
1
)
−2
, (11.76)
can be shown to be an upper bound for
1
4
δ
2
1
+ 1. Choosing, for example,
α = α
−1
1
yields tr P V = α
2
1
+ 2. △
11.3 A Dissipative Systems Perspective on Robust Stability
Although th e Lyapunov-function-based robust analysis fr amework discussed
in Section 11.2 applies to p roblems in which the nominal nonlinear system
dynamics f
0
(·) are perturbed by an uncertain function ∆f(·) ∈ ∆, a
reinterpretation of these results yield standard nonlinear s ys tem theoretic
criteria when viewed from the terminals of the uncertain parts of the system.
For example, the boundin g function
Γ(x) =
1
4
V
′
(x)G
δ
(x)G
T
δ
(x)V
′T
(x) + m
T
(h
δ
(x))m(h
δ
(x))
in Proposition 11.1 forms the basis of nonlinear H
∞
theory while the
bounding fu nction
Γ(x) =
1
4
[m(h
δ
(x)) + G
T
δ
(x)V
′T
(x)]
T
[m(h
δ
(x)) + G
T
δ
(x)V
′T
(x)]
+V
′
(x)G
δ
(x)m
1
(h
δ
(x))
in Proposition 11.2 forms the basis for nonlinear passivity and dissip ativity
theory. In particular, every operator δ(·) ∈ ∆, where ∆ is given by (11.25),
is dissipative with respect to the supply rate r(y, u
0
) = y
T
y −γ
2
u
T
0
u
0
, where
u
0
= δ(y).
Now, it follows from the results in Section 6.2 that the zero solution
x(t) ≡ 0 of th e nonlinear uncertain system (11.16) is globally asymptotically
stable for all δ(·) ∈ ∆ if the nonlinear system G given by
˙x(t) = f
0
(x) + G
δ
(x)u
0
(t), x(0) = x
0
, t ≥ 0, (11.77)
y(t) = h
δ
(x(t)), (11.78)
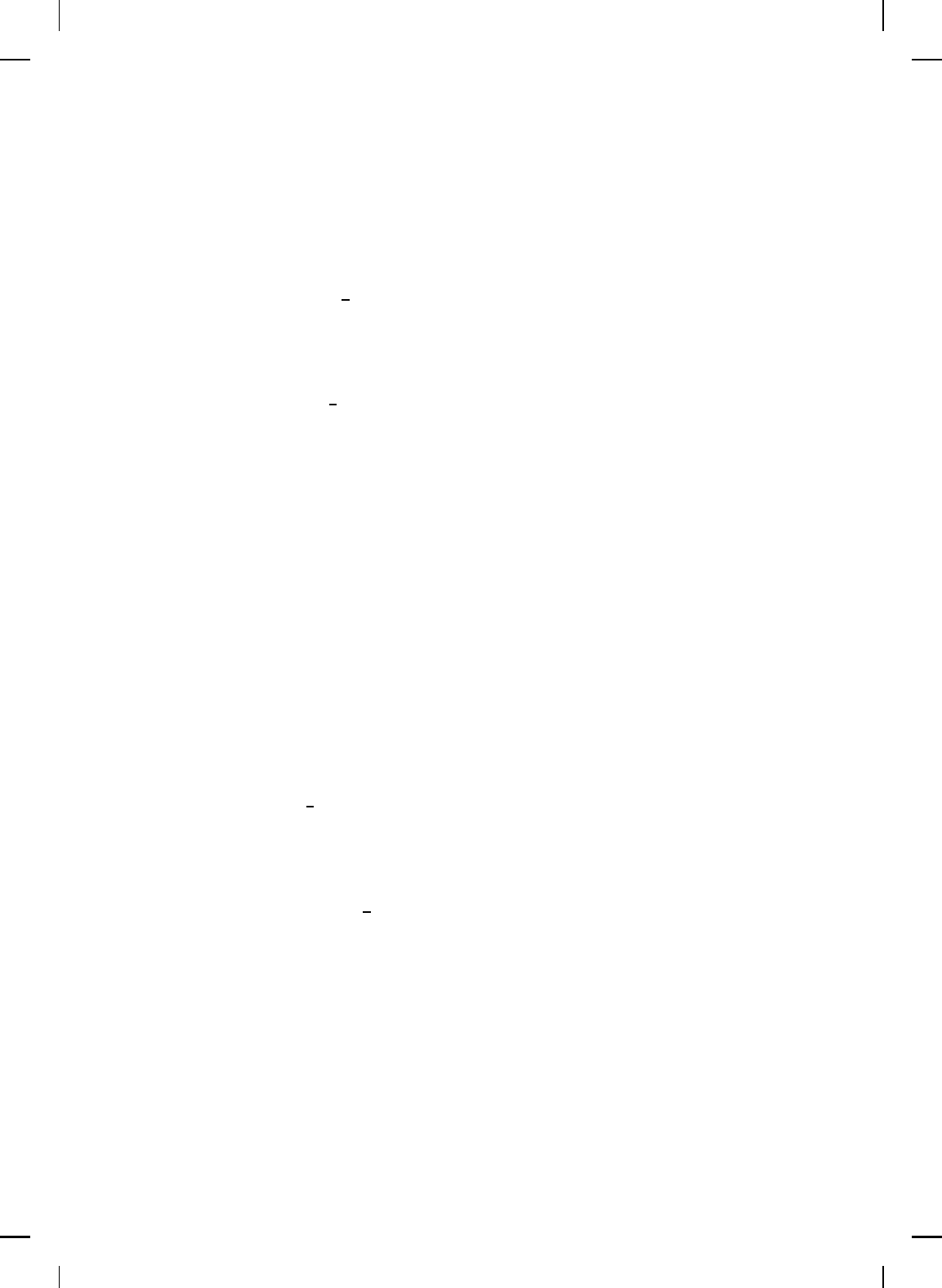
NonlinearBook10pt November 20, 2007
ROBUST NONLINEAR CONTROL 667
is dissipative with respect to the supply rate r(u
0
, y) = γ
2
u
T
0
u
0
− y
T
y.
Hence, it follows from Corollary 5.3 that a sufficient condition for robust
stability of (11.16) is the existence of functions ℓ(·), W(·), and a continuously
differentiable radially unbounded storage function V (·) su ch that
0 = V
′
(x)f
0
(x) + h
T
δ
(x)h
δ
(x) + ℓ
T
(x)ℓ(x), (11.79)
0 =
1
2
V
′
(x)G
δ
(x) + ℓ
T
(x)W(x), (11.80)
0 = γ
2
I − W
T
(x)W(x), (11.81)
or, equivalently,
0 ≥ V
′
(x)f
0
(x) +
1
4
γ
−2
V
′
(x)G
δ
(x)G
T
δ
(x)V
′T
(x) + h
T
δ
(x)h
δ
(x), x ∈ R
n
,
(11.82)
which is identical to (11.36) with m(y) = γ
−1
y an d L
1
(x) ≥ 0, x ∈ R
n
, for
the uncertainty structure ∆ given by (11.24).
Similarly, every operator δ(·) ∈ ∆, where ∆ is given by (11.27) with
m
1
(y) = M
1
y, m
2
(y) = M
2
y, and M
1
, M
2
∈ S
m
such that M
1
M
2
+M
2
M
1
≤
0, is dissipative w ith respect to the supply rate r(y, u
0
) = −(u
0
−M
1
y)
T
(u
0
−
M
2
y), where u
0
= δ(y). Now, it follows from the results in Section 6.2
that th e zero solution x(t) ≡ 0 of the nonlinear uncertain s ystem (11.16)
is globally asymptotically stable for all δ(·) ∈ ∆ if the nonlinear s y s tem G
given by (11.77) and (11.78) is dissipative with respect to the supply rate
r(u
0
, y) = (u
0
− M
1
y)
T
(u
0
− M
2
y). Hence, it follows from Theorem 5.6
that a sufficient condition for robust stability of (11.16) is the existence of
functions ℓ(·), W(x) and a continuously differentiable r ad ially unbounded
storage function V (·) such that
0 = V
′
(x)f
0
(x) − h
T
δ
(x)M
1
M
2
h
δ
(x) + ℓ
T
(x)ℓ(x), (11.83)
0 =
1
2
V
′
(x)G
δ
(x) − h
T
δ
(x)(M
1
+ M
2
) + ℓ
T
(x)W(x), (11.84)
0 = I − W
T
(x)W(x), (11.85)
or, equivalently,
0 ≥ V
′
(x)f
0
(x) +
1
4
[Mh
δ
(x) + G
T
δ
(x)V
′T
(x)]
T
·[Mh
δ
(x) + G
T
δ
(x)V
′T
(x)] + V
′
(x)G
δ
(x)M
1
h
δ
(x), x ∈ R
n
,
(11.86)
where M
△
= M
2
− M
1
, which is identical to (11.39) with m
1
(y) = M
1
y,
m
2
(y) = M
2
y, and L
1
(x) ≥ 0, x ∈ R
n
, f or the uncertainty structure ∆ given
by (11.27). The above exposition demonstrates that dissipativity theory and
nonlinear robustness theory are derivable from the same principles an d are
part of the same mathematical framework.

NonlinearBook10pt November 20, 2007
668 CHAPTER 11
To see this f or linear Ω-bound theory, rewrite (11.50) as
˙x(t) = Ax(t) + ∆Ax(t), x(0) = x
0
, t ≥ 0. (11.87)
Next, rewrite (11.87) as a negative feedback interconnection of a nominal
system and an u ncertain operator given by
˙x(t) = Ax(t) −u(t), x(0) = x
0
, t ≥ 0, (11.88)
y(t) = x(t), u
c
(t) = y(t), (11.89)
y
c
(t) = ∆Au
c
(t), u(t) = −y
c
(t), (11.90)
or, equivalently, as a negative feedback interconnection given in Figure 11.1
where
G = G(s) ∼
A −I
n
I
n
0
and G
c
= ∆A.
G(s)
∆A
6
-
+
–
Figure 11.1 Feedback interconnection of G(s) and ∆A.
The following two propositions show that Ω-bound theory f or robus t
stability analysis is indeed a special case of dissipativity theory.
Proposition 11.13. Let ∆A ∈ ∆
A
denote a linear operator ∆A :
R
n
→ R
n
with in put u
c
and output y
c
. Let Ω : S
n
→ S
n
be such that for
every P ∈ S
n
,
∆A
T
P + P ∆A ≤ Ω(P ). (11.91)
Then the linear operator ∆A(·) is dissipative with respect to the supply rate
r
c
(u
c
, y
c
) = u
T
c
Ω(P )u
c
−2y
T
c
P u
c
.
Proof. The proof is a direct consequence of (11.91) by noting that y
c
=
∆Au
c
, and hence, for every u
c
∈ R
n
, r
c
(u
c
, y
c
) = u
T
c
Ω(P )u
c
− 2y
T
c
P u
c
≥ 0.

NonlinearBook10pt November 20, 2007
ROBUST NONLINEAR CONTROL 669
Proposition 11.14. Let
G(s) ∼
A − I
n
I
n
0
and assume that there exists P = P
T
> 0 such that
0 > A
T
P + P A + Ω(P ). (11.92)
Then the linear dynamical system given by the transfer fun ction G(s) with
input u and output y is exponentially dissipative with respect to the supply
rate r(u, y) = −y
T
Ω(P )y − 2y
T
P u.
Proof. It follows from (11.92) that there exists a scalar ε > 0 such
that 0 ≥ A
T
P + P A + εP + Ω(P ). The result now follows immediately f rom
Theorem 6.2 with B = −I
n
, C = I
n
, D = 0, Q = −Ω(P ), R = 0, S = − P ,
W = 0, and L = (−A
T
P − P A − εP − Ω(P ))
1/2
.
In light of Propositions 11.13 an d 11.14, it follows fr om Theorem 6.2,
with G = G(s), G
c
= ∆A(·), Q = −R
c
= −Ω(P ), R = Q
c
= 0, S =
S
c
= −P , and σ = 1, that if (11.91) and (11.92) hold, then A + ∆A is
asymptotically stable for all ∆A ∈ ∆
A
. This of course establishes that Ω-
bound theory for robust stability analysis is a special case of dissipativity
theory. This exposition thus demonstrates that all (parameter-independent)
guaranteed cost bounds developed in the literature including the boun ded
real bound [11, 147, 337, 356], the positive r eal bound [8, 147], the shifted
bounded real bound [435], the shifted positive real bound [435], the implicit
small gain bound [161], the absolute value bound [83], the linear bound
[41,50,221,243], the inverse bound [50], the d ouble commutator bound [436],
the shifted linear bound [53], and the shifted inverse bound [53] are a special
case of dissipativity theory.
11.4 Robust Optimal Control for Nonlinear Uncertain Systems
In this section, we consider a control problem for nonlinear uncertain
dynamical s ystems involving a notion of optimality with respect to an
auxiliary cost which guarantees a bound on the worst-case value of a
nonlinear-nonquadratic cost criterion over a prescribed uncertainty set. The
optimal robust feedback controllers are derived as a direct consequence of
Theorem 11.1 and provide a generalization of the Hamilton-Jacobi-Bellman
conditions for time-invariant, infinite-horizon problems for addressing robust
feedback controllers of nonlinear uncertain systems. To address the robust
optimal control problem let D ⊂ R
n
be an open set and let U ⊂ R
m
, where
0 ∈ D and 0 ∈ U. Furthermore, let F ⊂ {F : D × U → R
n
: F (0, 0) = 0}.

NonlinearBook10pt November 20, 2007
670 CHAPTER 11
Next, consider the controlled uncertain dyn amical system
˙x(t) = F (x(t), u(t)), x(0) = x
0
, t ≥ 0, (11.93)
where F (·, ·) ∈ F and the control u(·) is restricted to the class of admissible
controls consisting of measurab le functions u(·) such that u(t) ∈ U for all
t ≥ 0, where the control constraint set U is given. We assume 0 ∈ U. Given
a control law φ(·) and a feedback control law u(t) = φ(x(t)), the closed-loop
system has the form
˙x(t) = F (x(t), φ(x(t))), x(0) = x
0
, t ≥ 0, (11.94)
for all F (·, ·) ∈ F.
Next, we present a generalization of Theorem 8.2 for characterizing
robust feedback controllers that guarantee robust stability over a class
of nonlinear uncertain systems and min imize an auxiliary performance
functional. For the statement of this result let L : D × U → R and define
the set of r egulation controllers for the nominal nonlinear system F
0
(·, ·) by
S(x
0
)
△
= {u(·) : u(·) is admissible and x(·) given by (11.93)
satisfies x(t) → 0 as t → ∞ with F (·, ·) = F
0
(·, ·)}.
Theorem 11.2. Consider the nonlinear uncertain controlled system
(11.93) with performance functional
J
F
(x
0
, u(·))
△
=
Z
∞
0
L(x(t), u(t))dt, (11.95)
where F (·, ·) ∈ F and u(·) is an admissible control. Assume that there exist
functions V : D → R, Γ : D × U → R, and control law φ : D → U, where
V (·) is a continuously differentiable function, such th at
V (0) = 0, (11.96)
V (x) > 0, x ∈ D, x 6= 0, (11.97)
φ(0) = 0, (11.98)
V
′
(x)F (x, φ(x)) ≤ V
′
(x)F
0
(x, φ(x)) + Γ(x, φ(x)), x ∈ D, F (·, ·) ∈ F,
(11.99)
V
′
(x)F
0
(x, φ(x)) + Γ(x, φ(x)) < 0, x ∈ D, x 6= 0, (11.100)
H(x, φ(x)) = 0, x ∈ D, (11.101)
H(x, u) ≥ 0, x ∈ D, u ∈ U, (11.102)
where F
0
(·, ·) ∈ F defines the n omin al system and
H(x, u)
△
= L(x, u) + V
′
(x)F
0
(x, u) + Γ(x, u). (11.103)
Then, with the feedback control u(·) = φ(x(·)), the zero solution x(t) ≡
0 of the closed-loop system (11.94) is locally asymptotically stable for all
NonlinearBook10pt November 20, 2007
ROBUST NONLINEAR CONTROL 671
F (·,
.
) ∈ F and there exists a neighborhood of the origin D
0
⊆ D such that
sup
F (·,·)∈F
J
F
(x
0
, φ(x(·))) ≤ J(x
0
, φ(x(·))) = V (x
0
), x
0
∈ D
0
, (11.104)
where
J(x
0
, u(·))
△
=
Z
∞
0
[L(x(t), u(t)) + Γ(x(t), u(t))]dt, (11.105)
and w here u(·) is admissible and x(t), t ≥ 0, solves (11.93) with F (x(t), u(t))
= F
0
(x(t), u(t)). In addition, if x
0
∈ D
0
then the feedback control u(·) =
φ(x(·)) minimizes J(x
0
, u(·)) in the sense th at
J(x
0
, φ(x(·))) = min
u(·)∈S(x
0
)
J(x
0
, u(·)). (11.106)
Finally, if D = R
n
and
V (x) → ∞ as kxk → ∞, (11.107)
then the zero solution x(t) ≡ 0 of the closed-loop system (11.94) is globally
asymptotically stable for all F (·) ∈ F.
Proof. Local and global asymptotic stability are a direct consequence
of (11.96)–(11.100) by applying Theorem 11.1 to the closed-loop system
(11.94). Furthermore, using (11.101), condition (11.104) is a restatement of
(11.11) as applied to the closed-loop system (11.94). Next, let u(·) ∈ S(x
0
)
and let x(·) be the solution of (11.93) with F (·, ·) = F
0
(·, ·). Then (11.106)
follows from Theorem 8.2 with L(x, u) replaced by L(x, u) + Γ(x, u) and
J(x
0
, u(·)) replaced by J(x
0
, u(·)).
Note that conditions (11.101) and (11.102) correspond to the steady-
state Hamilton-Jacobi-Bellman conditions for th e nominal nonlinear s ys tem
F
0
(·, ·) with th e auxiliary cost of J(x
0
, u(·)). If F consists of only th e
nominal nonlinear closed-loop sys tem F
0
(·, ·), then Γ(x, u) = 0 for all x ∈ D
and u ∈ U satisfies (11.99), and hence, J
F
(x
0
, u(·)) = J(x
0
, u(·)). In this
case, T heorem 11.2 specializes to Theorem 8.2.
Next, we specialize T heorem 11.2 to linear uncertain systems and pro-
vide conn ections to th e quadratic Lyapunov bounding synthesis framework
developed in [48, 51]. Specifically, we consider F to be the set of uncertain
linear systems given by
F = {(A + ∆A)x + (B + ∆B)u : x ∈ R
n
, A ∈ R
n×n
, B ∈ R
n×m
,
(∆A, ∆B) ∈ ∆
A
× ∆
B
}, (11.108)
where ∆
A
⊂ R
n×n
and ∆
B
⊂ R
n×m
are given bounded uncertainty sets of
the uncertain perturbations (∆A, ∆B) of the nominal system (A, B) such
that (0, 0) ∈ ∆
A
× ∆
B
. For the f ollowing result let R
1
∈ P
n
and R
2
∈ P
m

NonlinearBook10pt November 20, 2007
672 CHAPTER 11
be given.
Corollary 11.3. Consider the linear uncertain controlled system
˙x(t) = (A + ∆A)x(t) + (B + ∆B)u(t), x(0) = x
0
, t ≥ 0, (11.109)
with performance functional
J
∆
˜
A
(x
0
, u(·))
△
=
Z
∞
0
[x
T
(t)R
1
x(t) + u
T
(t)R
2
u(t)]dt, (11.110)
where u(·) is admissible and (∆A, ∆B) ∈ ∆
A
× ∆
B
. Furthermore, assume
there exist P ∈ P
n
, Ω
xx
: P
n
→ N
n
, Ω
xu
: P
n
→ R
n×m
, and Ω
uu
: P
n
→ N
m
such that
∆A
T
P + P ∆A − P ∆B(R
2
+ Ω
uu
(P ))
−1
(B
T
P + Ω
T
xu
(P ))
−(B
T
P + Ω
T
xu
(P ))
T
(R
2
+ Ω
uu
(P ))
−1
∆B
T
P ≤ Ω
xx
(P )
−Ω
xu
(P )(R
2
+ Ω
uu
(P ))
−1
(B
T
P + Ω
T
xu
(P ))
−(B
T
P + Ω
T
xu
(P ))
T
(R
2
+ Ω
uu
(P ))
−1
Ω
T
xu
(P )
+(B
T
P + Ω
T
xu
(P ))
T
(R
2
+ Ω
uu
(P ))
−1
Ω
uu
(P )(R
2
+ Ω
uu
(P ))
−1
·(B
T
P + Ω
T
xu
(P )), (∆A, ∆B) ∈ ∆
A
× ∆
B
, (11.111)
and
0 = A
T
P + P A + R
1
+ Ω
xx
(P )
−(B
T
P + Ω
T
xu
(P ))
T
(R
2
+ Ω
uu
(P ))
−1
(B
T
P + Ω
T
xu
(P )). (11.112)
Then, with the feedback control u = φ(x) = −(R
2
+ Ω
uu
(P ))
−1
(B
T
P +
Ω
T
xu
(P ))x, the zero s olution x(t) ≡ 0 to (11.109) is globally asymptotically
stable for all x
0
∈ R
n
and (∆A, ∆B) ∈ ∆
A
× ∆
B
, and
sup
(∆A,∆B)∈∆
A
×∆
B
J
∆
˜
A
(x
0
, φ(x(·))) ≤ J(x
0
, φ(x(·))) = x
T
0
P x
0
, (11.113)
where
J(x
0
, u(·))
△
=
Z
∞
0
[x
T
(t)R
1
x(t) + u
T
(t)R
2
u(t) + x
T
(t)Ω
xx
(P )x(t)
+2x
T
(t)Ω
xu
(P )u(t) + u
T
(t)Ω
uu
(P )u(t)]dt, (11.114)
and where u(·) is admissible and x(t), t ≥ 0, solves (11.109) w ith
(∆A, ∆B) = (0, 0). Fu rthermore,
J(x
0
, φ(x(·))) = min
u(·)∈S(x
0
)
J(x
0
, u(·)), (11.115)
where S(x
0
) is the set of regulation controllers for the nominal system and
x
0
∈ R
n
.
Proof. The result is a direct consequ en ce of Theorem 11.2 with
F (x, u) = (A + ∆A)x+ (B +∆B)u, F
0
(x, u) = Ax+ Bu, L(x, u) = x
T
R
1
x+

NonlinearBook10pt November 20, 2007
ROBUST NONLINEAR CONTROL 673
u
T
R
2
u, V (x) = x
T
P x, Γ(x, u) = x
T
Ω
xx
(P )x + 2x
T
Ω
xu
(P )u + u
T
Ω
uu
(P )u,
D = R
n
, and U = R
m
. Specifically, cond itions (11.96) and (11.97) are
trivially satisfied. Now, forming x
T
(11.111)x it follows that, after some
algebraic manipulation, V
′
(x)F (x, φ(x)) ≤ V
′
(x)F
0
(x, φ(x)) + Γ(x, φ(x)),
for all (∆A, ∆B) ∈ ∆
A
× ∆
B
. Furthermore, it follows from (11.112)
that H(x, φ(x)) = 0, and hence, V
′
(x)F
0
(x, φ(x)) + Γ(x, φ(x)) < 0 for
all x 6= 0. Thus, H(x, u) = H(x, u) − H(x, φ(x)) = [u − φ(x)]
T
(R
2
+
Ω
uu
(P ))[u−φ(x)] ≥ 0 so that all the conditions of Theorem 11.2 are satisfied.
Finally, since V (·) is radially unbounded, (11.109), with u(t) = φ(x(t)) =
−(R
2
+Ω
uu
(P ))
−1
(B
T
P + Ω
T
xu
(P ))x(t), is globally asymptotically stable for
all (∆A, ∆B) ∈ ∆
A
× ∆
B
.
Note that in the case where U = R
m
the robust feedback control
u = φ(x) is globally optimal since it minimizes H(x, u) and satisfies (11.101).
Specifically, setting
∂
∂u
H(x, u) = 0, (11.116)
yields the robust feedback control
φ(x) = −(R
2
+ Ω
uu
(P ))
−1
(B
T
P + Ω
T
xu
(P ))x. (11.117)
Now, since
∂
2
∂u
2
H(x, u) = R
2
+ Ω
uu
(P ) > 0, (11.118)
it follows that for all x ∈ R
n
the robust feedback control given by (11.117)
minimizes H(x, u). In p articular, the optimal feedback control law φ(x)
in Corollary 11.3 is derived using the properties of H(x, u) as defined in
Theorem 11.2. Specifically, since H(x, u) = x
T
(A
T
P +P A+R
1
+Ω
xx
(P ))x+
u
T
(R
2
+ Ω
uu
)u + 2x
T
(B
T
P + Ω
T
xu
(P ))
T
u it follows that ∂
2
H/∂u
2
> 0. Now,
∂H/∂u = 2(R
2
+Ω
uu
(P ))u+2(B
T
P +Ω
T
xu
(P ))x = 0 gives the unique global
minimum of H(x, u). Hence, since φ(x) minimizes H(x, u) it follows that
φ(x) satisfies ∂H/∂u = 0 or, equivalently, (R
2
+ Ω
uu
(P ))φ(x) + (B
T
P +
Ω
T
xu
(P ))x = 0 so that φ(x) is given by (11.117). Similar remarks hold for
the nonlinear robust controllers developed in Sections 11.4 and 11.5.
In order to make explicit connections with linear robust control, we
now assign explicit structure to the sets ∆
A
and ∆
B
and the bounding
functions Ω
xx
(·), Ω
xu
(·), and Ω
uu
(·). First, the uncertainty set ∆
A
×∆
B
is
assumed to be of the form
∆
A
× ∆
B
△
=
(
(∆A, ∆B) : ∆A =
p
X
i=1
δ
i
A
i
, ∆B =
p
X
i=1
δ
i
B
i
,
p
X
i=1
δ
2
i
α
2
i
≤ 1
)
,
(11.119)
where for i = 1, . . . , p : A
i
∈ R
n×n
and B
i
∈ R
n×m
are fixed matrices
denoting the structure of the parametric uncertainty, α
i
is a given positive
NonlinearBook10pt November 20, 2007
674 CHAPTER 11
number, and δ
i
is an uncertain real parameter. As discuss ed in Section
11.2 the uncertain parameters δ
i
are assumed to lie in a specified ellipsoidal
region in R
p
[50,51]. In this case, let
Ω
xx
(P ) =
p
X
i=1
α
2
i
α
A
T
i
P A
i
+ αP,
Ω
xu
(P ) =
p
X
i=1
α
2
i
α
A
T
i
P B
i
,
Ω
uu
(P ) =
p
X
i=1
α
2
i
α
B
T
i
P B
i
,
where α is an arbitrary positive scalar. Next, for notational convenience
define R
2s
△
= R
2
+
P
p
i=1
α
2
i
α
B
T
i
P B
i
and P
s
△
= B
T
P +
P
p
i=1
α
2
i
α
B
T
i
P A
i
. Now,
note that
0 ≤
p
X
i=1
α
i
α
1
2
P
1
2
(A
i
− B
i
R
−1
2s
P
s
) −
δ
i
α
1
2
α
i
P
1
2
T
·
α
i
α
1
2
P
1
2
(A
i
−B
i
R
−1
2s
P
s
) −
δ
i
α
1
2
α
i
P
1
2
,
or, equivalently,
p
X
i=1
δ
i
[(A
i
− B
i
R
−1
2s
P
s
)
T
P + P (A
i
− B
i
R
−1
2s
P
s
)]
≤
p
X
i=1
α
2
i
α
(A
i
− B
i
R
−1
2s
P
s
)
T
P (A
i
− B
i
R
−1
2s
P
s
) +
δ
2
i
α
α
2
i
P,
which, since
P
p
i=1
δ
2
i
α
2
i
≤ 1, implies
p
X
i=1
δ
i
[(A
i
− B
i
R
−1
2s
P
s
)
T
P + P (A
i
− B
i
R
−1
2s
P
s
)]
≤
p
X
i=1
α
2
i
α
(A
i
− B
i
R
−1
2s
P
s
)
T
P (A
i
− B
i
R
−1
2s
P
s
) + αP,
and h en ce, (11.111) holds. Fu rthermore, (11.112) specializes to
0 = A
T
α
P + P A
α
+ R
1
+
p
X
i=1
α
2
i
α
A
T
i
P A
i
− P
T
s
R
−1
2s
P
s
, (11.120)
where A
α
△
= A +
α
2
I
n
, and the optimal robust feedback law is given by
φ(x) = −R
−1
2s
P
s
x. This corresponds to the resu lts obtained in [41,243].
