Haddad W.M. Nonlinear Dynamical Systems and Control: A Lyapunov-Based Approach

Подождите немного. Документ загружается.

NonlinearBook10pt November 20, 2007

ROBUST NONLINEAR CONTROL 685

−L

(x) − Γ

(x)

≤ φ

(x)R

−1

(x)φ(x) + V

′

(x)G(x)σ(φ(x))

≤

i=1

(x)y

+ 2σ

(−y

)),

which implies the result.

The following result specializes Theorem 11.3 to linear uncertain

systems.

Corollary 11.6. Consider the uncertain linear dynamical system G

given by (11.109) and (11.169) with ∆B ≡ 0, where φ(x) = −(R

Ω

(P ))

−1

P + Ω

(P ))x and where P ∈ P

, satisﬁes (11.111) and

(11.112). Furthermore, assu me R

= diag[r

, . . . , r

], where r

> 0,

i = 1, . . . , m. Then the linear system G has a sector (and, hence, gain)

margin (

, ∞).

Next, we introduce the notion of robust control Lyapunov functions

for the nonlinear dynamical system (11.125).

Deﬁnition 11.1. Consider the controlled n on linear dynamical system

given by (11.125). A continuously diﬀerentiable positive-deﬁnite function

V : R

→ R satisfying

′

(x)f

(x) + Γ

(x) < 0, x ∈ R, (11.171)

where R

△

= {x ∈ R

: x 6= 0 : V

′

(x)G(x) = 0}, is called a robust control

Lyapunov func tion.

Finally, we show that for every nonlinear dynamical system for w hich a

robust control Lyapunov function can be constructed there exists an inverse

optimal robust feedback control law with sector and gain margin (

, ∞).

Theorem 11.4. Consider th e nonlinear dynamical system G given by

(11.125) and let the continuously diﬀerentiable positive-deﬁnite, radially

unbounded function V : R

→ R be a robust control Lyapunov function

of (11.125), that is,

′

(x)f

(x) + Γ

(x) < 0, x ∈ R, (11.172)

where R

△

= {x ∈ R

: x 6= 0 : V

′

(x)G(x) = 0}. Then, with the feedback

control law given by

φ(x) =







−



α(x)+

√

(x)+(β

(x)β(x))

(x)β(x)



β(x), β(x) 6= 0,

0, β(x) = 0,

(11.173)

NonlinearBook10pt November 20, 2007

686 CHAPTER 11

where α(x)

△

= V

′

(x)f

(x) + Γ

(x), β(x)

△

= G

(x)V

′T

(x), and c

> 0, the

nonlinear system G given by (11.125) has a sector (and, hence, gain) margin

(

, ∞).

Proof. The result is a direct consequence of Corollary 11.5 and

Theorem 11.3 with R

(x) =

2η(x)

and L

(x) = −α(x) +

η(x)

(x)β(x),

where

η(x) =







−



α(x)+

√

(x)+(β

(x)β(x))

(x)β(x)



, β(x) 6= 0,

0, β(x) = 0.

(11.174)

Speciﬁcally, note that R

(x) > 0, x ∈ R

, and

(x) = −α(x) +

η(x)

(x)β(x)











−



(x)β(x) − α(x)

(x) + (β

(x)β(x))



, β(x) 6= 0,

−α(x), β(x) = 0.

(11.175)

Now, it follows from (11.175) that L

(x) ≥ 0, β(x) 6= 0, and s ince V (·)

is a robust control Lyapunov function of (11.125), it follows that L

(x) =

−α(x) ≥ 0, for all x ∈ R. Hence, (11.175) yields L

(x) ≥ 0, x ∈ R

, so that

all the conditions of Corollary 11.5 are satisﬁed.

11.8 Rob u st Nonlinear Controllers with Polynomial

Performance Criteria

In this section, we specialize the results of Section 11.5 to linear s ys tems con-

trolled by n onlinear controllers that minimize a polynomial cost functional.

Speciﬁcally, assume F to be the set of uncertain systems given by

F = {(A + ∆A)x + Bu : x ∈ R

, u ∈ R

, A ∈ R

n×n

, B ∈ R

n×m

, ∆A ∈ ∆

(11.176)

where ∆

⊂ R

n×n

is a given bounded uncertainty set of the uncertain

perturbation ∆A of the nominal system A such that 0 ∈ ∆

. For simplicity

of exposition here and in the remainder of the chapter we assume ∆B = 0.

For the following result recall the deﬁnition of S and let R

∈ P

, R

∈ P

and

∈ N

, k = 2, . . . , r, be given where r is a positive integer.

Theorem 11.5. Consider the linear uncertain controlled system

˙x(t) = (A + ∆A)x(t) + Bu(t), x(0) = x

, t ≥ 0, (11.177)

where u(·) ∈ U is admissible and ∆A ∈ ∆

. Ass ume there exists Ω : P

→

such that

∆A

P + P ∆A ≤ Ω(P ), ∆A ∈ ∆

, P ∈ P

, (11.178)

NonlinearBook10pt November 20, 2007

ROBUST NONLINEAR CONTROL 687

and there exist P ∈ P

and M

∈ N

, k = 2, . . . , r, such that

0 = A

P + P A + R

+ Ω(P ) −P SP, (11.179)

and

0 = (A − SP )

+ M

(A −SP ) +

+ Ω(M

), k = 2, . . . , r. (11.180)

Then, w ith the feedback control law

u = φ(x) = −R

−1

P +

k=2

k−1

the zero solution x(t) ≡ 0 of the uncertain system (11.177) is globally

asymptotically stable for all x

∈ R

and ∆A ∈ ∆

, and the performance

functional (11.127) satisﬁes

sup

∆A∈∆

∆A

, φ(x(·))) ≤ J(x

, φ(x(·))) = x

P x

k=2

)

(11.181)

where

J(x

, u(·))

△

∞

[L(x, u) + Γ(x, u)]dt, (11.182)

and where u(·) is admissible, and x(t), t ≥ 0, solves (11.177) with ∆A = 0,

and

Γ(x, u) = x

(Ω(P ) +

k=2

k−1

Ω(M

))x,

where u(·) is admissible and ∆A ∈ ∆

. In addition, the performance

functional (11.127), with R

(x) = R

, L

(x) = 0, and

(x) = x

k=2

k−1

k=2

k−1

·S

k=2

k−1

is minimized in the sense that

J(x

, φ(x(·))) = min

u(·)∈S(x

)

J(x

, u(·)), (11.183)

where S(x

) is the set of regulation controllers for the nominal system and

∈ R

Proof. The result is a direct consequence of Corollary 11.4 with

(x) = Ax, G

(x) = B, ∆f(x) = ∆Ax, ∆G(x) = 0, ∆ = ∆

NonlinearBook10pt November 20, 2007

688 CHAPTER 11

and V (x) = x

P x+

k=2

. Speciﬁcally, conditions (11.128)–

(11.162) are trivially satisﬁed. Now, it follows from (11.178) that

0 ≥ x

(∆A

P + P ∆A −Ω(P ))x

k=2

k−1

(∆A

+ M

∆A − Ω(M

))x,

x ∈ R

, w hich implies (11.133) for all ∆A ∈ ∆

so that all the conditions

of Corollary 11.4 are satisﬁed.

Theorem 11.5 generalizes the deterministic version of the stochastic

nonlinear-nonquadratic optimal control problem considered in [411] to the

robustness setting. Furthermore, unlike the results of [411], Theorem 11.5

is not limited to sixth order cost functionals and cubic nonlinear controllers

since it addresses a polynomial nonlinear performance criterion. Theorem

11.5 requires the solutions of r − 1 modiﬁ ed Riccati equations in (11.180)

to obtain the optimal robust controller. However, if

, k = 3, . . . , r,

then M

= M

, k = 3, . . . , r, satisﬁes (11.180). In this case, we r equ ir e the

solution of one modiﬁed Riccati equation in (11.180). This special case is

considered in Propositions 11.17 and 11.18 below.

As d iscussed in C hapter 9, the performance functional (11.182) is a

derived performance functional in the sense that it cannot be arb itrarily

speciﬁed. However, this performance functional does weight the state

variables by arbitrary even powers. Furthermore, (11.182) has the form

∆A

, u(·)) =

∞

k=2

k−1

)x + u

+φ

(x)R

(x)

dt,

where φ

(x) is the nonlinear part of the optimal feedback control

φ(x) = φ

(x) + φ

(x),

where φ

(x)

△

= −R

−1

P x and φ

(x)

△

= −R

−1

k=2

k−1

Next, we consider the special case in which r = 2. In this case, note

that if there exist P ∈ P

and M

∈ N

such that

0 = A

P + P A + R

+ Ω(P ) − P SP

and

0 = (A −SP )

+ M

(A −SP ) +

+ Ω(M

then (11.177), with the performance functional

∆A

, u(·)) =

∞

x + u

u + (x

x)(x

NonlinearBook10pt November 20, 2007

ROBUST NONLINEAR CONTROL 689

+(x

x)]dt,

is globally asymptotically stable for all x

∈ R

and ∆A ∈ ∆

with the

feedback control law u = φ(x) = −R

−1



P + (x

x)M



Finally, using the explicit uncertainty characterizations given by

(11.121) and (11.122) (with ∆B = 0) we present two specializations of

Theorem 11.5.

Proposition 11.17. Consider the linear uncertain controlled system

˙x(t) = (A + ∆A)x(t) + Bu(t), x(0) = x

, t ≥ 0, (11.184)

where u(·) ∈ U is admissible and ∆A ∈ ∆

, where ∆

is given by (11.121).

Assume that there exist P ∈ P

and M

∈ N

such that

0 = A

P + P A

+ R

i=1

P A

− P SP, (11.185)

0 = (A

− SP )

+ M

− SP ) +

i=1

. (11.186)

Then, w ith the feedback control

u = φ(x) = −R

−1

P +

k=2

k−1

the zero solution x(t) ≡ 0 to the un certain system (11.184) is globally

asymptotically stable for all x

∈ R

and ∆A ∈ ∆

, and the performance

functional (11.127) satisﬁes

sup

∆A∈∆

∆A

, φ(x(·))) ≤ J(x

, φ(x(·))) = x

P x

k=2

)

(11.187)

where

J(x

, u(·))

△

∞

[L(x, u) + Γ(x, u)]dt, (11.188)

and where u(·) is admissible, and x(t), t ≥ 0, solves (11.184) with ∆A = 0

and

Γ(x, u) = x

i=1

P A

+ αP

k=2

k−1

i=1

+ αM

In addition, the performance functional (11.127), w ith R

(x) = R

, L

(x) =

NonlinearBook10pt November 20, 2007

690 CHAPTER 11

0, and

(x) = x





k=2

k−1

k=2

k−1





(11.189)

is minimized in the sense that

J(x

, φ(x(·))) = min

u(·)∈S(x

)

J(x

, u(·)), (11.190)

where S(x

) is the set of regulation controllers for the nominal system and

∈ R

Proof. It need only be noted that ∆A

P + P ∆A ≤

i=1

P A

αP for all ∆A ∈ ∆

and P ∈ P

. The result now is a d irect consequence

of Theorem 11.5 with Ω(P ) =

i=1

P A

+ αP .

Proposition 11.18. Consider the linear u ncertain controlled sys tem

˙x(t) = (A + ∆A)x(t) + Bu(t), x(0) = x

, t ≥ 0, (11.191)

where u(·) ∈ U is admissible and ∆A ∈ ∆

, wh ere ∆

is given by (11.122).

Assume that there exist P ∈ P

and M

∈ N

such that

0 = A

P + P A + R

+ C

+ P B

P − P SP, (11.192)

0 = (A − SP )

+ M

(A −SP ) +

+ C

+ M

(11.193)

Then, with the f eedback control

u = φ(x) = −R

−1

P +

k=2

k−1

the zero solution x(t) ≡ 0 to the un certain system (11.191) is globally

asymptotically stable for all x

∈ R

and ∆A ∈ ∆

, and the performance

functional (11.127) satisﬁes

sup

∆A∈∆

∆A

, φ(x(·))) ≤ J(x

, φ(x(·))) = x

P x

k=2

)

(11.194)

where

J(x

, u(·))

△

∞

[L(x, u) + Γ(x, u)]dt, (11.195)

and where u(·) is admissible, and x(t), t ≥ 0, solves (11.191) with ∆A = 0

and

Γ(x, u) = x



+ P B

NonlinearBook10pt November 20, 2007

ROBUST NONLINEAR CONTROL 691

k=2

k−1

+ M

)

In addition, the performance functional (11.127), w ith R

(x) = R

, L

(x) =

0, and

(x) = x





k=2

k−1

k=2

k−1





(11.196)

is minimized in the sense that

J(x

, φ(x(·))) = min

u(·)∈S(x

)

J(x

, u(·)), (11.197)

where S(x

) is the set of regulation controllers for the nominal system and

∈ R

Proof. It need only be noted that ∆A

P +P ∆A ≤ C

+P B

for all ∆A ∈ ∆

and P ∈ P

. The result now is a direct consequence of

Theorem 11.5 with Ω(P ) = C

+ P B

P .

Propositions 11.17 and 11.18 are generalizations of results given in

[48,50] to nonlinear polynomial performance criteria.

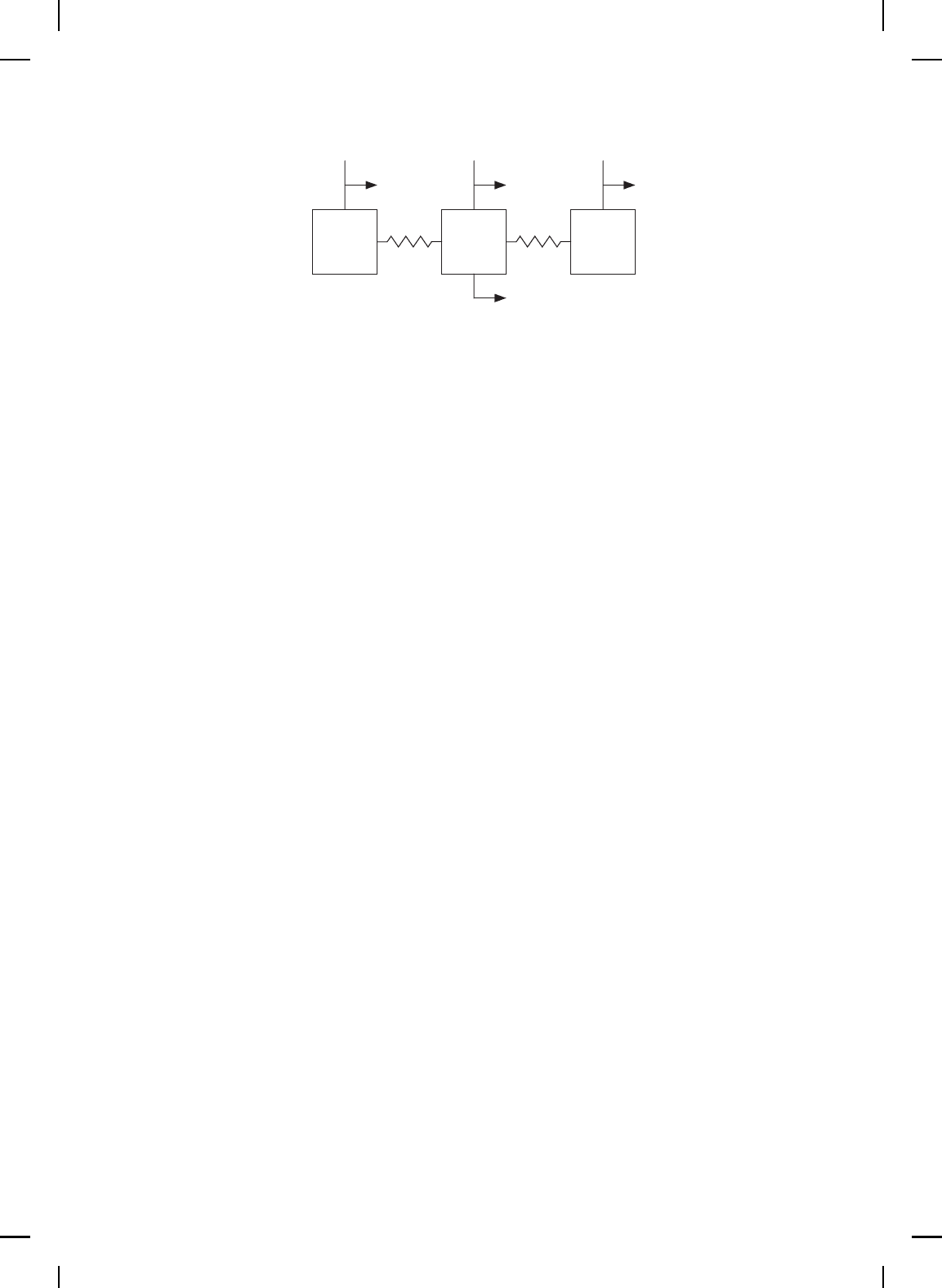
Example 11.7. Consider the three-mass, two-spring system shown in

Figure 11.3 with m

= m

= 1 and uncertain spring stiﬀnesses k

and k

. A control f orce acts on mass 2. T he nominal dynamics, with state

variables deﬁ ned in Figure 11.3, are given by

A =







0 0 0 1 0 0

0 0 0 0 1 0

0 0 0 0 0 1

−k

1nom

0 0 0 0

1nom

−(k

1nom

+ k

2nom

) k

2nom

0 0 0

0 k

2nom

−k

2nom

0 0 0







, B =













(11.198)

The actual spring stiﬀnesses can be written as k

= k

inom

+ ∆ k

, w here

inom

= 1, i = 1, 2, so that the actual dynamics of the system are given by

actual

= A +

i=1

∆k

, where







0 0 0 0 0 0

−1 1 0 0 0 0

1 −1 0 0 0 0

0 0 0 0 0 0







, A







0 0 0 0 0 0

0 −1 1 0 0 0

0 1 −1 0 0 0







NonlinearBook10pt November 20, 2007

692 CHAPTER 11

Figure 11.3 Three-mass oscillator.

Choosing the performance variables

△

= E

x + E

where



0 0 1 0 0 0

0 0 0 0 0 1



, E





expresses the desire to regulate the displacement and velocity of mass 3.

Furth ermore, let the design parameters R

= E

and R

= ρE

where ρ = 0.001. For the nonlinear control design, the add itional design

parameter

in (11.186) is taken as

= 10 · R

. The design goal of this

problem is to achieve good nominal perform an ce and demonstrate robust

stability and performance for pertu rbed spring stiﬀness values in the range

0.75 ≤ k

≤ 1.25, i = 1, 2.

Figures 11.4 and 11.5 compares the linear LQR controller to the

nonlinear Speyer [411] controller (Proposition 11.17 with ∆A = 0 and

r = 2) for the nominal plant subject to an initial displacement of mass

1. Note that the nonlinear controller achieves better performance in th e

sense of state trajectory regulation for each of the states. This is primarily

due to the relatively large in itial displacement of mass 1 which allowed the

nonlinear part of the control to initially have a signiﬁcant impact on the

response causing the position of mass 1 to approach zero faster than the

linear controller design. The action of the nonlinear part of the controller

also reduced the overshoot since the nonlinear control contribution becomes

greater as the position deviates farther from the equilibrium thus causing

the mass to recover qu icker.

Next, using Proposition 11.17 (with r = 2) a robustiﬁed nonlinear con-

troller was designed for the uncertain system with multivariable uncertainty

in the stiﬀness values. This controller is compared to the robustiﬁed linear

LQR controller given by (11.120), th e Speyer [411] nonlinear controller, and

the LQR controller. Figures 11.6 and 11.7 shows the state responses for these

designs for ∆k

= −0.25 and ∆k

= 0.25. Note th at the robust nonlinear

controller outperf orms all other controllers in the sense of worst-case state

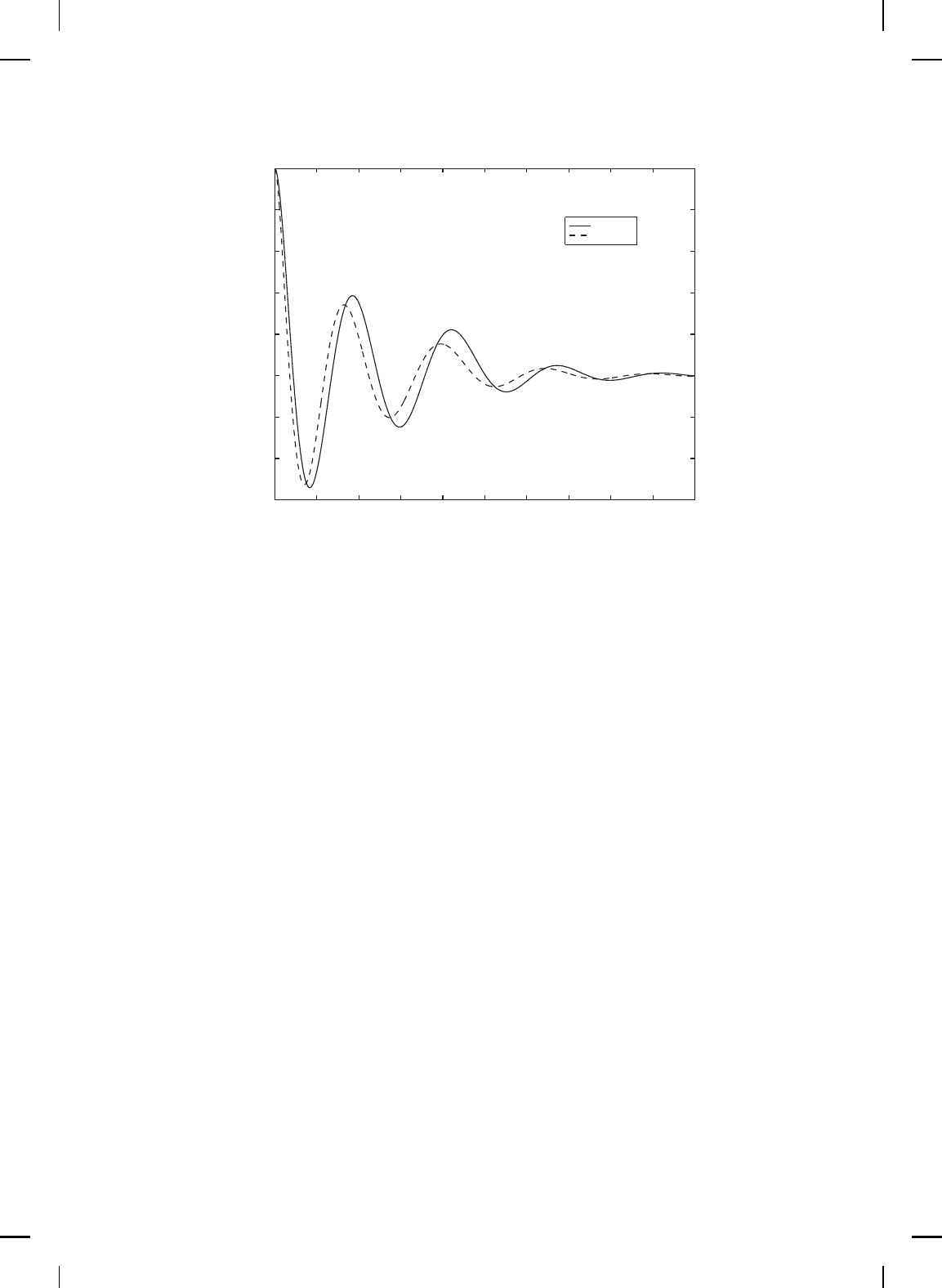
NonlinearBook10pt November 20, 2007

ROBUST NONLINEAR CONTROL 693

LQR

Speyer

0 1 2 3 4 5 6 7 8 9 10

-0.6

-0.4

-0.2

0.2

0.4

0.6

0.8

time (sec)

position of mass 1

Figure 11.4 Comparison of LQR and Speyer controllers for the nominal system: Position

of mass 1.

trajectory regulation. △

Example 11.8. Consider the pitch axis longitudinal dyn amics m odel

of th e F-16 ﬁghter aircraft system given in [394] for nomin al ﬂight conditions

at 3000 ft and Mach number of 0.6. The nominal model is given by





˙x

(t)

˙x

(t)

˙x

(t)









0 1.00 0

0 −0.87 43.22

0 0.99 − 1.34









(t)









0 0

−17.25 −1.58

−0.17 − 0.25







(t)



, (11.199)

where x

is the pitch angle, x

is the pitch rate, x

is the angle of attack, u

is the elevator deﬂection, and u

is the ﬂaperon deﬂection. Here, we consider

uncertainty in the (2,2) and (3,3) entries of the dynamics matrix. Using the

uncertainty structure given by (11.122), the actual dynamics are given by

actual

= A + B

F C

, where





0 0

1 0

0 1





, F =



0 f



, C



0 1 0

0 0 1



Using Proposition 11.18, with R

= 3·I

, R

= 0.001·I

= 10·R

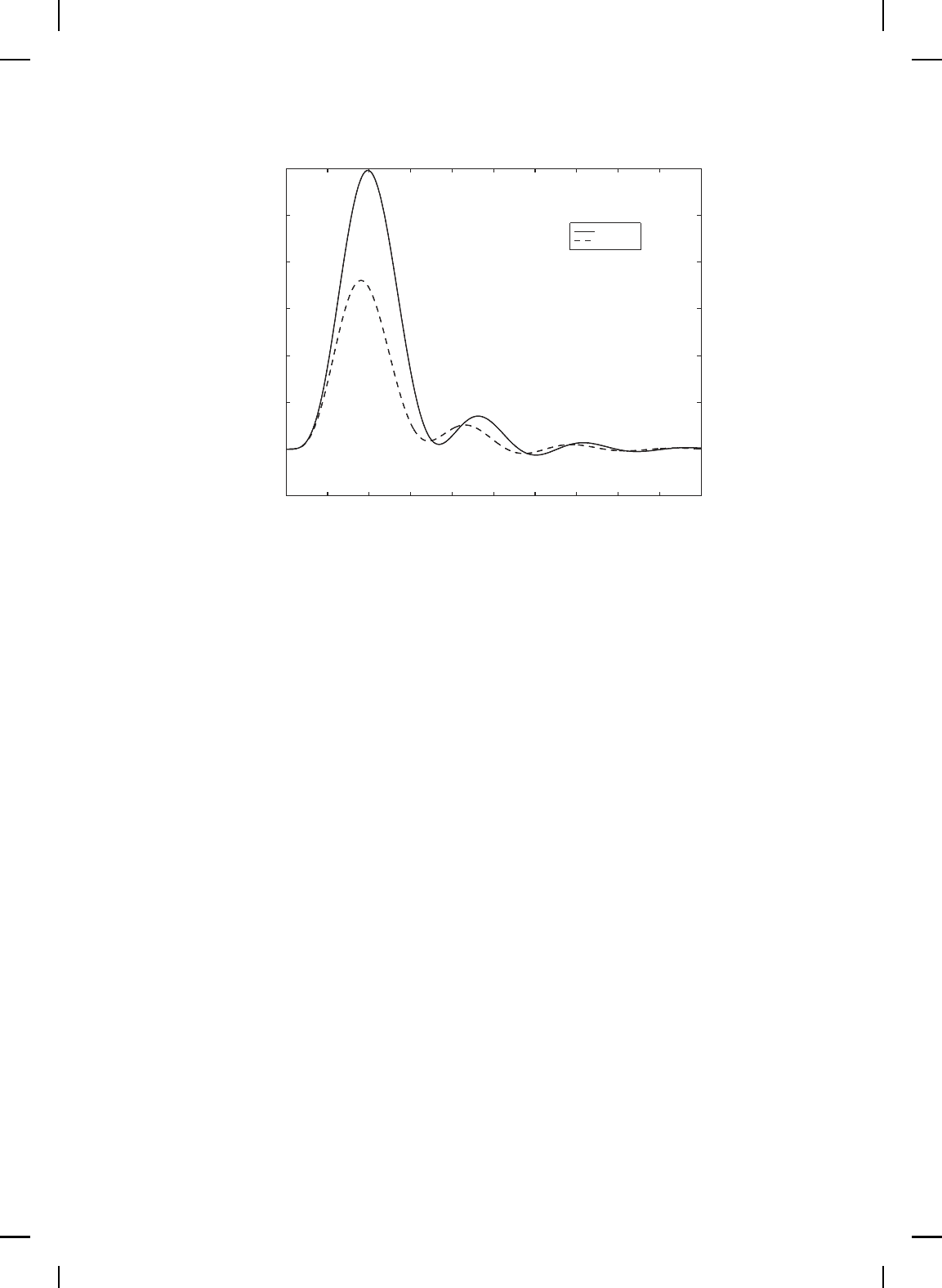
NonlinearBook10pt November 20, 2007

694 CHAPTER 11

LQR

Speyer

0 1 2 3 4 5 6 7 8 9 10

-0.02

0.02

0.04

0.06

0.08

0.1

0.12

time (sec)

position of mass 3

Figure 11.5 Comparison of LQR and Speyer controllers for the nominal system: Position

of mass 3.

| ≤ 1, |f

| ≤ 5, and r = 2, a robustiﬁed nonlinear controller was designed

for the un certain system. This controller is compared with the robustiﬁed

linear controller given by (11.123), the Speyer [411] n onlinear controller, and

the LQR controller. Figures 11.8 and 11.9 shows that for the case where f

−1 and f

= 5 the LQR controller destabilizes th e system while the nominal

Speyer [411] controller maintains Lyapunov stability. This demonstrates

the inherent robustness of the nominal (nonrobustiﬁed) nonlinear control

in comparison to the nomin al linear control. Furthermore, for the same

uncertainty range Figures 11.10 and 11.11 shows the state response for the

robustiﬁed nonlinear controller (Proposition 11.18) and the robustiﬁed linear

controller obtained via (11.123). △

11.9 Rob u st Nonlinear Controllers with Multilinear

Performance Criteria

In this section, we specialize the results of Section 11.5 to linear uncertain

systems controlled by nonlinear controllers that minimize a multilinear cost

functional. Speciﬁcally, we assum e F to be the set of uncertain linear

systems given by (11.176). For the following result recall the deﬁnition

of S and let R

∈ P

, R

∈ P

, and

2ν

∈ N

(2ν,n)

, ν = 2, . . . , r, be given

where r is a given integer.