Haddad W.M. Nonlinear Dynamical Systems and Control: A Lyapunov-Based Approach

Подождите немного. Документ загружается.

NonlinearBook10pt November 20, 2007

ROBUST NONLINEAR CONTROL 675

Alternatively, we can choose

Ω

(P ) =

i=1

− B

−1

P )

P (A

− B

−1

P ) + αP,

Ω

(P ) = 0,

Ω

(P ) = 0.

In this case, note that

0 ≤

i=1



− B

−1

P ) −





−B

−1

P ) −



or, equivalently,

i=1

[(A

− B

−1

P )

P + P (A

− B

−1

P )]

≤

i=1

−B

−1

P )

P (A

− B

−1

P ) +

which, since

i=1

≤ 1, implies

i=1

[(A

− B

−1

P )

P + P (A

− B

−1

P )]

≤

i=1

− B

−1

P )

P (A

− B

−1

P ) + αP,

and h en ce, (11.111) holds. Fu rthermore, (11.112) specializes to

0 = A

P + P A

+ R

i=1

− B

−1

P )

P (A

−B

−1

P ),

(11.121)

and the optimal robust feedback law is given by φ(x) = −R

−1

P x.

The robustiﬁed Riccati equation (11.121) does not appear to have been

considered in the literature for the uncertainty structure given by (11.119).

Next, we consider the uncertainty set ∆

× ∆

given by

∆

× ∆

△

= {(∆A, ∆B) : ∆A = B

F C

, ∆B = B

F D

, F

F ≤ N},

(11.122)

where B

∈ R

n×r

, C

∈ R

s×n

, and D

∈ R

r×m

are ﬁxed matrices denoting

the structure of the uncertainty, F ∈ R

r×s

is an uncertain matrix, and

NonlinearBook10pt November 20, 2007

676 CHAPTER 11

N ∈ N

is a given uncertainty bound [48]. I n this case, let

Ω

(P ) = C

+ P B

Ω

(P ) = C

Ω

(P ) = D

Next, for notational convenience deﬁne R

△

= R

+ D

and P

△

P + D

. Now, note that

0 ≤



F C

− F D

−1

− B





F C

− F D

−1

− B



or, equivalently,

[F C

− F D

−1

]

P + P B

[F C

− F D

−1

]

≤ [C

− D

−1

]

F [C

− D

−1

] + P B

which, since F

F ≤ N, implies

[F C

−F D

−1

]

P + P B

[F C

− F D

−1

]

≤ [C

− D

−1

]

N[C

− D

−1

] + P B

and h en ce, (11.111) holds. Fu rthermore, (11.112) specializes to

0 = A

P + P A + R

+ C

+ P B

P −P

−1

, (11.123)

and the optimal robust feedback law is given by φ(x) = − R

−1

x. This

corresponds to the results obtained in [41, 354, 356,480].

Alternatively, we can choose

Ω

(P ) = [C

− D

−1

P ]

N[C

− D

−1

P ] + P B

Ω

(P ) = 0,

Ω

(P ) = 0.

In this case, n ote that

0 ≤



F C

− F D

−1

P − B





F C

− F D

−1

P − B



or, equivalently,

[F C

− F D

−1

P ]B

P + P B

[F C

− F D

−1

P ]

≤ [C

− D

−1

P ]

F [C

− D

−1

P ] + P B

which, since F

F ≤ N, implies

[F C

− F D

−1

P ]B

P + P B

[F C

−F D

−1

P ]

≤ [C

− D

−1

P ]

N[C

−D

−1

P ] + P B

NonlinearBook10pt November 20, 2007

ROBUST NONLINEAR CONTROL 677

and h en ce, (11.111) holds. Fu rthermore, (11.112) becomes

0 = A

P + P A + R

− P SP + [C

− D

−1

P ]

N[C

− D

−1

P ]

+P B

P, (11.124)

where S

△

= BR

−1

, and the optimal robust feedback law is given by

φ(x) = −R

−1

P x.

The robustiﬁed Riccati equation (11.124) does not appear to have been

considered in the literature for the uncertainty structure given by (11.122).

11.5 Optimal and Inverse Optimal Robust Control for No n linear

Uncertain Aﬃne Systems

In this section, we specialize Theorem 11.2 to aﬃne (in the control) uncertain

systems having the form (see Figure 11.2)

˙x(t) = f

(x(t))+∆f(x(t))+[G

(x(t)) + ∆G(x(t))] u(t), x(0) = x

, t ≥ 0,

(11.125)

where f

: R

→ R

satisﬁes f

(0) = 0, G

: R

→ R

n×m

, D = R

, U = R

F = {f

(x) + ∆f(x) + [G

(x) + ∆G(x)]u : x ∈ R

, u ∈ R

, (∆f, ∆G) ∈

∆

× ∆

}, ∆f(·) ∈ ∆

⊂ {∆f : R

→ R

: ∆ f (0) = 0},

and

∆G ∈ ∆

⊂ {∆G : R

→ R

n×m

In this s ection, no explicit structure is assumed for the elements of ∆

and

∆

. In Section 11.6 the str ucture of variations in ∆

and ∆

will be

speciﬁed. Furthermore, we consider performance integrands L(x, u) of the

form

L(x, u) = L

(x) + L

(x)u + u

(x)u, (11.126)

where L

: R

→ R, L

: R

→ R

1×m

, and R

: R

→ P

so that (11.95)

becomes

J(x

, u(·)) =

∞

(x(t)) + L

(x(t))u(t) + u

(t)R

(x)u(t)]dt. (11.127)

Corollary 11.4. Consider the nonlinear uncertain controlled aﬃne

system (11.125) with performance functional (11.127). Assume that there

exist a continuously diﬀerentiable function V : R

→ R an d functions

: R

→ R

1×m

, Γ

: R

→ R, Γ

: R

→ R

1×m

, and Γ

: R

→ N

such that

V (0) = 0, (11.128)

(0) = 0, (11.129)

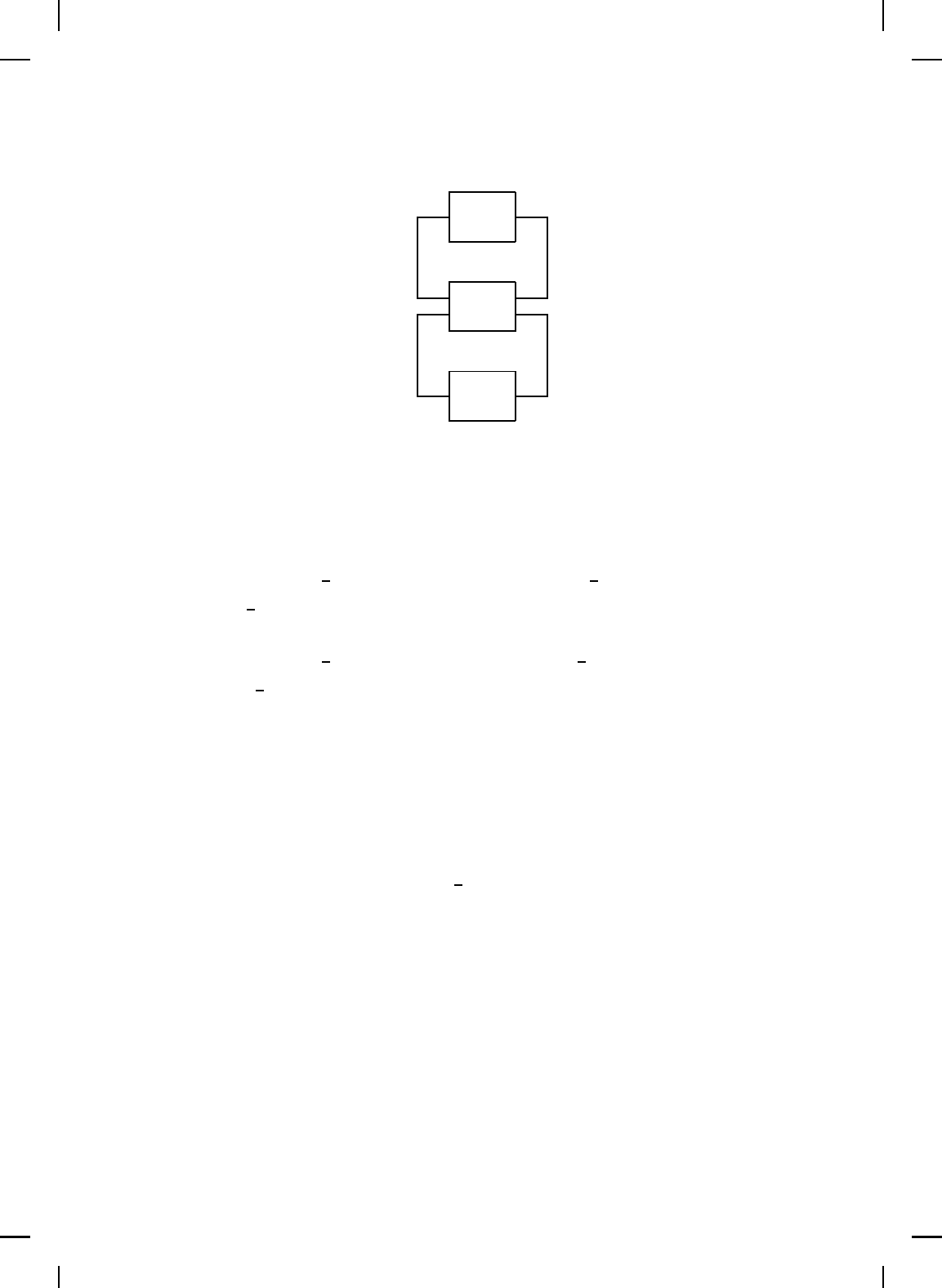
NonlinearBook10pt November 20, 2007

678 CHAPTER 11

φ(x)

∆G



Figure 11.2 Uncertain nonlinear feedback system.

(0) = 0, (11.130)

V (x) > 0, x ∈ R

, x 6= 0, (11.131)

′

(x)



∆f(x) −

∆G(x)R

−1

(x)V

(x)



≤ Γ

(x) −

(x)R

−1

(x)V

(x)

(x)R

−1

(x)Γ

(x)R

−1

(x)V

(x), (∆f, ∆ G) ∈ ∆

× ∆

(11.132)

′

(x)[f

(x) −

(x)R

−1

(x)V

(x)] + Γ

(x) −

(x)R

−1

(x)V

(x)

(x)R

−1

(x)Γ

(x)R

−1

(x)V

(x) < 0, x ∈ R

, x 6= 0,

(11.133)

and

V (x) → ∞ as kxk → ∞, (11.134)

where R

(x)

△

= R

(x)+Γ

(x) and V

(x)

△

= [L

(x)+Γ

(x)+V

′

(x)G

(x)]

Then the zero solution x(t) ≡ 0 of the nonlinear uncertain s ystem (11.125)

is globally asymptotically stable for all (∆f, ∆G) ∈ ∆

× ∆

with the

feedback control law

φ(x) = −

−1

(x)V

(x), (11.135)

and the performan ce functional (11.127) satisﬁes

sup

(∆f,∆G)∈∆

×∆

J(x

, φ(x(·))) ≤ J(x

, φ(x(·))) = V (x

), (11.136)

where

J(x

, u(·))

△

∞

[L(x(t), u(t)) + Γ(x(t), u(t))]dt, (11.137)

and

Γ(x, u) = Γ

(x) + Γ

(x)u + u

(x)u, (11.138)

NonlinearBook10pt November 20, 2007

ROBUST NONLINEAR CONTROL 679

where u(·) is admissible, and x(t), t ≥ 0, solves (11.125) with (∆f, ∆G) =

(0, 0). In addition, the perform ance fu nctional (11.137), with

(x) = φ

(x)R

(x)φ(x) −V

′

(x)f

(x) − Γ

(x), (11.139)

is minimized in the sense that

J(x

, φ(x(·))) = min

u(·)∈S(x

)

J(x

, u(·)). (11.140)

Proof. The result is a direct consequence of Theorem 11.2 with

D = R

, U = R

, F

(x, u) = f

(x) + G

(x)u, F (x, u) = f

(x) + ∆f(x) +

(x) + ∆G(x)]u, F = {f

(x) + ∆f(x) + [G

(x) + ∆G(x)]u : x ∈ R

, u ∈

, (∆f, ∆G) ∈ ∆

×∆

}, L(x, u) given by (11.126), and Γ(x, u) given by

(11.138). Speciﬁcally, with (11.125), (11.126), and (11.138), the Hamiltonian

has the form

H(x, u) = L

(x) + L

(x)u + u

(x)u + V

′

(x)(f

(x) + G

(x)u)

+Γ

(x) + Γ

(x)u + u

(x)u.

Now, the feedback control law (11.135) is obtained by setting

∂H

∂u

= 0. With

(11.135), it follows that (11.132) and (11.133) imply (11.99), and (11.100),

respectively. Next, since V (·) is continuously diﬀerentiable and x = 0 is

a local minimum of V (·), it follows that V

′

(0) = 0, and hence, since by

assumption L

(0) = 0 and Γ

(0) = 0, it follows that φ(0) = 0, which proves

(11.98). Next, with L

(x) given by (11.139) and φ(x) given by (11.135) it

follows that (11.101) holds. Finally, since H(x, u) = H(x, u) −H(x, φ(x)) =

[u − φ(x)]

(x)[u − φ(x)] and R

(x) is positive deﬁnite for all x ∈ R

condition (11.102) holds. The result now f ollows as a direct consequence of

Theorem 11.2.

Note that (11.133) implies

V (x)

△

= V

′

(x)[f

(x) + ∆f(x) + (G

(x) + ∆G(x))φ(x)] < 0,

x ∈ R

, x 6= 0, (∆f, ∆G) ∈ ∆

× ∆

, (11.141)

with φ(x) given by (11.135). Furthermore, (11.128), (11.131), and (11.141)

ensure that V (x) is a Lyapunov function guaranteeing robust stability of

the closed-loop system for all (∆f, ∆G) ∈ ∆

× ∆

. As n oted in Chapter

9, it is important to recognize that the function L

(x) which appears in th e

integrand of the performance functional (11.127) is an arbitrary function

of x subject to conditions (11.129), (11.132), and (11.133). Thus, L

(x)

provides ﬂexibility in choosing the control law.

With L

(x) given by (11.139) and φ(x) given by (11.135), L(x, u) +

Γ(x, u) can be expressed as

L(x, u) + Γ(x, u) = [u −φ(x)]

(x)[u − φ(x)] −V

′

(x)[f

(x) + G

(x)u]

NonlinearBook10pt November 20, 2007

680 CHAPTER 11



u +

−1

(x)(L

(x) + Γ

(x))



(x)



u +

−1

(x)(L

(x) + Γ

(x))



−V

′

(x)[f

(x) + G

(x)φ(x)]

−

′

(x)G

(x)R

−1

(x)G

(x)V

′T

(x). (11.142)

Since R

(x) ≥ R

(x) > 0 for all x ∈ R

the ﬁrst term of the right-hand

side of (11.142) is nonnegative, while (11.141) implies that the second term

is nonnegative. Thus, we have

L(x, u) + Γ(x, u) ≥ −

′

(x)G

(x)R

−1

(x)G

(x)V

′T

(x), (11.143)

which shows that L(x, u) + Γ(x, u) may be negative. As a result, there

may exist a control in put u for which the auxiliary performance functional

J(x

, u) is negative. Note, however, if the control is a stabilizing feedback

control, that is, u ∈ S(x

), then it follows from (11.136) and (11.140) that

J(x

, u(·)) ≥ V (x

) ≥ 0, x

∈ R

, u(·) ∈ S(x

Furth ermore, in this case, substituting u = φ(x) into (11.142) yields

L(x, φ(x)) + Γ(x, φ(x)) = −V

′

(x)[f

(x) + G

(x)φ(x)],

which, by (11.141), is positive.

11.6 Nonlinear Guaranteed Cost Control

Having established the theoretical basis for our approach, we now assign

explicit structure to the s et ∆

× ∆

and the bounding functions Γ

(x),

(x), and Γ

(x), x ∈ R

. Even th ou gh both ∆f (x) and ∆G(x), x ∈ R

uncertainties can be considered, for simplicity of exposition we assume that

∆G(x) = 0, x ∈ R

(see Problem 11.26 for the case w here ∆G(x) 6= 0,

x ∈ R

). The uncertainty set F is assumed to be of the form given by

(11.23) with ∆ given by (11.24).

Proposition 11.15. Consider the nonlinear uncertain controlled sys-

tem (11.125) with performance functional (11.127). Assume that there

exist a continuously diﬀerentiable function V : R

→ R and function

: R

→ R

1×m

such that (11.128)–(11.131) are satisﬁed,

′

(x)[f

(x) −

(x)R

−1

(x)V

(x)] +

′

(x)G

(x)V

′T

(x)

(x))m(h

(x)) < 0, x ∈ R

, x 6= 0, (11.144)

and

V (x) → ∞ as kxk → ∞, (11.145)

where V

(x)

△

= [L

(x) + V

′

(x)G

(x)]

. Then th e zero solution x(t) ≡ 0 of

the nonlinear uncertain system (11.125) is globally asymptotically stable for

NonlinearBook10pt November 20, 2007

ROBUST NONLINEAR CONTROL 681

all δ(·) ∈ ∆, w here ∆ is given by (11.24), with the feedback control law

φ(x) = −

−1

(x)V

(x). (11.146)

Furth ermore, the performance functional (11.127) satisﬁes

sup

δ(·)∈∆

J(x

, φ(x(·))) ≤ J(x

, φ(x(·))) = V (x

), (11.147)

where

J(x

, u(·))

△

∞

(x) + L

(x)u + u

(x)u +

′

(x)G

(x)V

′T

(x)

(x))m(h

(x))]dt, (11.148)

where u(·) is admissible and x(t), t ≥ 0, s olves (11.125) with δ(h

(x)) ≡ 0.

In addition, the performance functional (11.148), with

(x) = φ

(x)R

(x)φ(x) − V

′

(x)f

(x) −

′

(x)G

(x)V

′T

(x)

−m

(x))m(h

(x)), (11.149)

is minimized in the sense that

J(x

, φ(x(·))) = min

u(·)∈S(x

)

J(x

, u(·)). (11.150)

Proof. The result is direct consequence of Corollary 11.4 with ∆

∆, ∆ given by (11.24), ∆G = 0, Γ

(x) =

′

(x)G

(x)V

′T

(x) +

(x))m(h

(x)), Γ

(x) = 0, and Γ

(x) = 0. Speciﬁcally, (11.128)–

(11.131) are satisﬁed by assum ption and (11.144) implies (11.133). Next, if

δ(·) ∈ ∆ it f ollows that

′

(x)∆f(x) −Γ

(x) = V

′

(x)G

(x)δ(h

(x)) −

′

(x)G

(x)V

′T

(x)

−m

(x))m(h

(x))

≤ −[

(x)V

′T

(x) − δ(h

(x))]

·[

(x)V

′T

(x) − δ(h

(x))]

≤ 0,

which implies (11.132). The result now follows as a direct consequence of

Corollary 11.4.

We now assign a diﬀerent structure to the uncertainty set ∆ and the

bounding functions Γ

(x), Γ

(x), and Γ

(x). Speciﬁcally, the uncertainty

set ∆ is assumed to be of the form given by (11.27).

Proposition 11.16. Consider the nonlinear uncertain controlled sys-

tem (11.125) with perform ance functional (11.127). Assume that there

exist a continuously diﬀerentiable function V : R

→ R and function

NonlinearBook10pt November 20, 2007

682 CHAPTER 11

: R

→ R

1×m

such that (11.128)–(11.131) are satisﬁed,

′

(x)[f

(x) −

(x)R

−1

(x)V

(x)] +

[m(h

(x)) + G

(x)V

′T

(x)]

·[m(h

(x)) + G

(x)V

′T

(x)] + V

′

(x)G

(x)m

(x)) < 0, x ∈ R

, x 6= 0,

(11.151)

and

V (x) → ∞ as kxk → ∞, (11.152)

where V

(x)

△

= [L

(x) + V

′

(x)G

(x)]

. Then th e zero solution x(t) ≡ 0 of

the nonlinear uncertain system (11.125) is globally asymptotically stable for

all δ(·) ∈ ∆, w here ∆ is given by (11.27), with the feedback control law

φ(x) = −

−1

(x)V

(x). (11.153)

Furth ermore, the performance functional (11.127) satisﬁes

sup

δ(·)∈∆

J(x

, φ(x(·))) ≤ J(x

, φ(x(·))) = V (x

), (11.154)

where

J(x

, u(·))

△

∞



(x) + L

(x)u + u

(x)u

[m(h

(x)) + G

(x)V

′T

(x)]

[m(h

(x)) + G

(x)V

′T

(x)]

′

(x)G

(x)m

(x))



dt, (11.155)

where u(·) is admissible, and x(t), t ≥ 0, solves (11.125) with δ(h

(x)) ≡ 0.

In addition, the performance functional (11.155), with

(x) = φ

(x)R

(x)φ(x) −V

′

(x)f

(x) − V

′

(x)G

(x)m

(x))

−

[m(h

(x)) + G

(x)V

′T

(x)]

[m(h

(x)) + G

(x)V

′T

(x)],

(11.156)

is minimized in the sense that

J(x

, φ(x(·))) = min

u(·)∈S(x

)

J(x

, u(·)). (11.157)

Proof. The result is direct consequence of Corollary 11.4 w ith

∆

= ∆, ∆ given by (11.27), ∆G = 0, Γ

(x) =

[m(h

(x)) +

(x)V

′T

(x)]

[m(h

(x))+ G

(x)V

′T

(x)]+ V

′

(x)G

(x)m

(x)), Γ

(x) =

0, and Γ

(x) = 0. Speciﬁcally, (11.128)–(11.131) are satisﬁed by

assumption and (11.151) implies (11.133). Next, if δ(·) ∈ ∆ it follows that

′

(x)∆f(x) − Γ

(x)

≤ −[δ(h

(x)) −m

(x))]

[δ(h

(x)) −m

(x))]

′

(x)G

(x)δ(h

(x))

NonlinearBook10pt November 20, 2007

ROBUST NONLINEAR CONTROL 683

−

[m(h

(x)) + G

(x)V

′T

(x)]

[m(h

(x)) + G

(x)V

′T

(x)]

−V

′

(x)G

(x)m

(x))

= −[

m(h

(x)) +

(x)V

′T

(x) − (δ(h

(x) − m

(x)))]

·[

m(h

(x)) +

(x)V

′T

(x) − (δ(h

(x) − m

(x)))]

≤ 0,

which implies (11.132). The result now follows as a direct consequence of

Corollary 11.4.

11.7 Stability Margins, Meaningful Inverse Optimality, and

Robust Control Lyapunov Functions

In this section, we specialize the results of Section 11.5 to the case where

L(x, u) is nonnegative for all (x, u) ∈ R

× R

. Here, we assu me that

(x) ≡ 0 and L

(x) ≥ 0, x ∈ R

. We begin by specializing Corollary

11.4 to the case where L

(x) ≡ 0. In th is case, the performance functional

(11.127) becomes

J(x

, u(·)) =

∞

(x(t)) + u

(t)R

(x(t))u(t)]dt. (11.158)

For simplicity of exposition we assume ∆G(x) ≡ 0, Γ

(x) ≡ 0, and

(x) ≡ 0.

Corollary 11.5. Consid er the nonlinear controlled dynamical system

(11.125) with performance functional (11.158). Assume that there exist a

continuously diﬀerentiable function V : R

→ R and a function Γ

: R

→

R su ch that

V (0) = 0, (11.159)

V (x) > 0, x ∈ R

, x 6= 0, (11.160)

′

(x)∆f(x) ≤ Γ

(x), ∆f(·) ∈ ∆, (11.161)

0 = V

′

(x)f

(x) + L

(x) −

′

(x)G(x)R

−1

(x)G

(x)V

′T

(x) + Γ

(x),

x ∈ R

, (11.162)

and

V (x) → ∞ as kxk → ∞. (11.163)

Furth ermore, assume that the system (11.125), with output y = L

(x), is

zero-state observable. Then the zero solution x(t) ≡ 0 of the u ncertain

closed-loop system

˙x(t) = f

(x(t)) + ∆f(x) + G(x(t))φ(x(t)), x(0) = x

, t ≥ 0,

(11.164)

NonlinearBook10pt November 20, 2007

684 CHAPTER 11

is globally asymptotically stable for all ∆f(·) ∈ ∆ with feedback control law

φ(x) = −

−1

(x)G

(x)V

′T

(x). (11.165)

Furth ermore, the performance functional (11.158) satisﬁes

J(x

, φ(x(·))) ≤ J(x

, φ(x(·))) = V (x

), (11.166)

where

J(x

, u(·))

△

∞

[L(x(t), u(t)) + Γ

(x(t))]dt. (11.167)

In addition, the performance functional (11.167) is minimized in the sense

that

J(x

, φ(x(·))) = min

u(·)∈S(x

)

J(x

, u(·)). (11.168)

Proof. The resu lt follows as a direct consequence of Corollary 11.4.

Next, we provide sector and gain margins for the nonlinear dynamical

system G given by (11.125). To consider relative stability margins for

nonlinear robust regulators consider the nonlinear dynamical system given

by (11.125) along with the output

y(t) = −φ(x(t)), (11.169)

where φ(·) is such that G is robus tly stable for all ∆f(·) ∈ ∆ with u = φ(x).

Furth ermore, assume that (11.125) and (11.169) is zero-state observable.

Theorem 11.3. Consider th e nonlinear dynamical system G given by

(11.125) and (11.169), where φ(x) is a feedback control law given by (11.165)

and where V (x), x ∈ R

, satisﬁes (11.159)–(11.162). Furthermore, assume

(x) = d iag[r

(x), . . . , r

(x)], where r

: R

→ R, r

(x) > 0, i = 1, . . . , m.

Then the nonlinear system G has a sector (and, hence, gain) margin (

, ∞).

Proof. Let ∆(u

) = σ(u

), where σ : R

→ R

is a static nonlinearity

such that σ(0) = 0, σ(u

) = [σ

), . . . , σ

)]

, and

< σ

for all u

6= 0, i = 1, . . . , m. In this case, the closed-loop system (11.125)

and (11.169) with u = −σ(y) is given by

˙x(t) = f

(x(t)) + ∆f(x(t)) + G(x(t))σ(φ(x(t))),

x(0) = x

, ∆f(·) ∈ ∆, t ≥ 0. (11.170)

Next, consider the Lyapunov function candidate V (x), x ∈ R

, satisfying

(11.162) and let

V (x) denote the Lyapunov derivative along with the

trajectories of the closed-loop system (11.170). Now, it follows from (11.161)

and (11.162) that f or all ∆f(·) ∈ ∆,

V (x) = V

′

(x)f

(x) + V

′

(x)∆f(x) + V

′

(x)G(x)σ(φ(x))

≤ φ

(x)R

−1

(x)φ(x) + V

′

(x)G(x)σ(φ(x)) + V

′

(x)∆f(x)