Haddad W.M. Nonlinear Dynamical Systems and Control: A Lyapunov-Based Approach
Подождите немного. Документ загружается.

NonlinearBook10pt November 20, 2007
ADVANCED STABILITY THEORY 235
Next, we provide two converse theorems for stability of time-varying
systems.
Theorem 4.8. Assume that the nonlinear time-varying dynamical
system (4.57) is u niformly asymptotically s table and f : [0, ∞) ×D → R
n
is
continuously differentiable. Let δ > 0 be such that B
δ
(0) ⊂ D is contained
in the domain of attraction of (4.57) and assume
∂f
∂x
is bounded on B
δ
(0)
uniformly in t. Then there exist a continuously differentiable function
V : [0, ∞) × B
δ
(0) → R and class K functions α(·), β(·), and γ(·) such
that
α(kxk) ≤ V (t, x) ≤ β(kxk), (t, x) ∈ [0, ∞) × B
δ
(0), (4.98)
˙
V (t, x) ≤ −γ(kxk), (t, x) ∈ [0, ∞) ×B
δ
(0). (4.99)
Proof. The proof is a direct consequence of T heorem 4.3 with n
1
= n,
n
2
= 1, x
1
(t − t
0
) = x(t), x
2
(t − t
0
) = t, f
1
(x
1
, x
2
) = f(t, x), f
2
(x
1
, x
2
) = 1,
and V (x
1
, x
2
) = V (t, x).
Theorem 4.9. Assume that the nonlinear time-varying dynamical
system (4.57) is (uniformly) exponentially stable and f : [0, ∞) × D → R
n
is continuously differentiable. Let δ > 0 be such that B
δ
(0) ⊂ D is
contained in the domain of attraction of (4.57) and assume
∂f
∂x
is bounded
on B
δ
(0) uniformly in t. Th en , for every p > 1, there exist a continuously
differentiable function V : [0, ∞) × B
δ
(0) → R and positive constants α, β,
and γ such that
αkxk
p
≤ V (t, x) ≤ βkxk
p
, (t, x) ∈ [0, ∞) ×B
δ
(0), (4.100)
˙
V (t, x) ≤ −γkxk
p
, (t, x) ∈ [0, ∞) × B
δ
(0). (4.101)
Proof. The proof is a direct consequence of T heorem 4.4 with n
1
= n,
n
2
= 1, x
1
(t − t
0
) = x(t), x
2
(t − t
0
) = t, f
1
(x
1
, x
2
) = f(t, x), f
2
(x
1
, x
2
) = 1,
and V (x
1
, x
2
) = V (t, x).
Finally, we state Lyapunov’s and Chetaev’s instability theorems for
time-varying systems. The proofs of these results are virtually identical
to the proofs of their time-invariant counterparts given in Section 3.6, and
hence, are left as an exercise for the reader.
Theorem 4.10. Consider the nonlinear dynamical system (4.57).
Assume that there exist a continuously differentiable fu nction V : [0, ∞) ×
D → R and class K functions β(·) and γ(·) such that
V (t, 0) = 0, t ∈ [0, ∞), (4.102)
V (t, x) ≤ β(kxk), (t, x) ∈ [0, ∞) × D, (4.103)

NonlinearBook10pt November 20, 2007
236 CHAPTER 4
˙
V (t, x) ≥ γ(kxk), (t, x) ∈ [0, ∞) × D. (4.104)
Furth ermore, assu me that for every sufficiently small δ > 0 there exist a
time t
0
≥ 0 an d x
0
∈ D such that kx
0
k < δ and V (t
0
, x
0
) > 0. Then the
zero solution x(t) ≡ 0 to (4.57) is u nstable.
Theorem 4.11. Consider the nonlinear dynamical system (4.57).
Assume that there exist a continuously differentiable fu nction V : [0, ∞) ×
D → R, a class K function β(·), a function W : [0, ∞) × D → R, a time
t
0
≥ 0, and scalars ε, λ > 0 such that
V (t
0
, 0) = 0, (4.105)
V (t, x) ≤ β(kxk), (t, x) ∈ [0, ∞) × D, (4.106)
W (t, x) ≥ 0, (t, x) ∈ [0, ∞) ×B
ε
(0), (4.107)
˙
V (t, x) ≥ λV (t, x) + W (t, x). (4.108)
Furth ermore, assume that for every sufficiently small δ > 0 there exists
x
0
∈ D such that kx
0
k < δ and V (t
0
, x
0
) > 0. Then the zero solution
x(t) ≡ 0 to (4.57) is unstable.
Theorem 4.12. Consider the nonlinear dynamical system (4.57).
Assume that there exist a continuously differentiable fu nction V : [0, ∞) ×
D → R, a class K function γ(·), a scalar ε > 0, and an open set Q ⊆ B
ε
(0)
such that
V (t, x) > 0, (t, x) ∈ [0, ∞) × Q (4.109)
sup
t≥0
sup
x∈Q
V (t, x) < ∞, (4.110)
0 ∈ ∂Q, (4.111)
V (t, x) = 0, (t, x) ∈ [0, ∞) × (∂Q ∩ B
ε
(0)), (4.112)
˙
V (t, x) ≥ γ(kxk), (t, x) ∈ [0, ∞) ×Q. (4.113)
Then the zero solution x(t) ≡ 0 to (4.57) is unstable.
4.4 Lagrange Stability, Bounde d ne ss, and Ultimate Boundedne ss
In the previous sections we introduced the concepts of stability and
partial stability for nonlinear dynamical systems. In certain engineering
applications, however, it is more natural to ascertain whether for every
system initial condition in a ball of radiu s δ the solution of the nonlinear
dynamical system is boun ded. T his leads to the notions of Lagrange stability,
boundedness, and ultimate boundedness. These notions are closely related
to what is known in the literature as practical stability. In this section, we
present Lyapunov-like th eorems for boundedness and ultimate boundedness
of nonlinear dynamical systems.

NonlinearBook10pt November 20, 2007
ADVANCED STABILITY THEORY 237
Definition 4.3. i) The nonlinear dynamical system (4.6) and (4.7) is
Lagrange stable with respect to x
1
if, for every x
10
∈ D and x
20
∈ R
n
2
, there
exists ε = ε(x
10
, x
20
) > 0 such that kx
1
(t)k < ε, t ≥ 0.
ii) The nonlinear dynamical system (4.6) and (4.7) is bounded with
re spect to x
1
uniformly in x
2
if there exists γ > 0 such that, for every
δ ∈ (0, γ), there exists ε = ε(δ) > 0 such that kx
10
k < δ implies kx
1
(t)k < ε,
t ≥ 0. The nonlinear dynamical system (4.6) and (4.7) is g lobally bounded
with respect to x
1
uniformly in x
2
if, for every δ ∈ (0, ∞), there exists
ε = ε(δ) > 0 such that kx
10
k < δ implies kx
1
(t)k < ε, t ≥ 0.
iii) T he nonlinear dynamical system (4.6) and (4.7) is ultimately boun-
ded with respect to x
1
uniformly in x
2
with bound ε if there exists γ > 0 such
that, for every δ ∈ (0, γ), there exists T = T (δ, ε) > 0 such that kx
10
k < δ
implies kx
1
(t)k < ε, t ≥ T . The nonlinear dynamical system (4.6) and (4.7)
is globally ultimately bounded with respect to x
1
uniformly in x
2
with bound
ε if, for every δ ∈ (0, ∞), there exists T = T (δ, ε) > 0 such that kx
10
k < δ
implies kx
1
(t)k < ε, t ≥ T .
Note that if a nonlinear dynamical system is globally bounded with
respect to x
1
uniformly in x
2
, th en it is Lagrange stable with respect to
x
1
. Alternatively, if a nonlinear dynamical system is (globally) bounded
with respect to x
1
uniformly in x
2
, then there exists ε > 0 such that it
is (globally) ultimately bounded with respect to x
1
uniformly in x
2
with a
bound ε. Conversely, if a nonlinear dynamical system is (globally) ultimately
bounded with respect to x
1
uniformly in x
2
with a bound ε, then it is
(globally) bou nded with respect to x
1
uniformly in x
2
. The following results
present Lyapunov-like theorems for boundedn ess and ultimate boundedness.
For these results define
˙
V (x
1
, x
2
)
△
= V
′
(x
1
, x
2
)f(x
1
, x
2
), where f (x
1
, x
2
)
△
=
[f
T
1
(x
1
, x
2
), f
T
2
(x
1
, x
2
)]
T
and V : D × R
n
2
→ R is a given continuously
differentiable function.
Theorem 4.13. C onsider the nonlinear dyn amical system (4.6) and
(4.7). Assume that there exist a continuously differentiable function V :
D × R
n
2
→ R and class K functions α(·), β(·) such that
α(kx
1
k) ≤ V (x
1
, x
2
) ≤ β(kx
1
k), x
1
∈ D, x
2
∈ R
n
2
, (4.114)
˙
V (x
1
, x
2
) ≤ 0, x
1
∈ D, kx
1
k ≥ µ, x
2
∈ R
n
2
, (4.115)
where µ > 0 is such that B
α
−1
(η)
(0) ⊂ D for some η ≥ β(µ). Then the
nonlinear dynamical system (4.6) and (4.7) is boun ded with respect to x
1
uniformly in x
2
. Furth ermore, for every δ ∈ (0, γ), x
10
∈ B
δ
(0) implies that
kx
1
(t)k ≤ ε, t ≥ 0, where
ε = ε(δ)
△
=
α
−1
(β(δ)), δ ∈ (µ, γ),
α
−1
(η), δ ∈ (0, µ],
(4.116)
NonlinearBook10pt November 20, 2007
238 CHAPTER 4
and γ
△
= sup{r > 0 : B
α
−1
(β(r))
(0) ⊂ D}. If, in addition, D = R
n
1
and
α(·) is a class K
∞
function, then the nonlinear dynamical system (4.6) and
(4.7) is globally bounded with respect to x
1
uniformly in x
2
and for every
x
10
∈ R
n
1
, kx
1
(t)k ≤ ε, t ≥ 0, where ε is given by (4.116) with δ = kx
10
k.
Proof. First, let δ ∈ (0, µ] and assu me kx
10
k ≤ δ. If kx
1
(t)k ≤ µ,
t ≥ 0, then it follows from (4.114) that kx
1
(t)k ≤ µ ≤ α
−1
(β(µ)) ≤ α
−1
(η),
t ≥ 0. Alternatively, if there exists T > 0 such that kx
1
(T )k > µ, then
it follows from the continuity of x
1
(·) that there exists τ < T such that
kx
1
(τ)k = µ and kx
1
(t)k ≥ µ, t ∈ [τ, T ]. Hence, it follows from (4.114) and
(4.115) that
α(kx
1
(T )k) ≤ V (x
1
(T ), x
2
(T )) ≤ V (x
1
(τ), x
2
(τ)) ≤ β(µ) ≤ η,
which implies that kx
1
(T )k ≤ α
−1
(η). Next, let δ ∈ (µ, γ) and assume
x
10
∈ B
δ
(0) and kx
10
k > µ. Now, for every
ˆ
t > 0 such that kx
1
(t)k ≥ µ,
t ∈ [0,
ˆ
t], it follows from (4.114) and (4.115) that
α(kx
1
(t)k) ≤ V (x
1
(t), x
2
(t)) ≤ V (x
10
, x
20
) ≤ β(δ), t ≥ 0,
which implies that kx
1
(t)k ≤ α
−1
(β(δ)), t ∈ [0,
ˆ
t]. Next, if there exists
T > 0 such that kx
1
(T )k ≤ µ, then it follows as in the proof of the first
case that kx
1
(t)k ≤ α
−1
(η), t ≥ T . Hence, if x
10
∈ B
δ
(0) \ B
µ
(0), then
kx
1
(t)k ≤ α
−1
(β(δ)), t ≥ 0. Finally, if D = R
n
1
and α(·) is a class K
∞
function it follows that β(·) is a class K
∞
function, an d hence, γ = ∞.
Hence, the n onlinear dynamical system (4.6) and (4.7) is globally bounded
with respect to x
1
uniformly in x
2
.
Theorem 4.14. C onsider the nonlinear dyn amical system (4.6) and
(4.7). Assume that there exist a continuously differentiable function V :
D × R
n
2
→ R and class K functions α(·), β(·) such that (4.114) holds.
Furth ermore, assume that there exists a continuous function W : D → R
such that W (x
1
) > 0, kx
1
k > µ, and
˙
V (x
1
, x
2
) ≤ −W (x
1
), x
1
∈ D, kx
1
k > µ, x
2
∈ R
n
2
, (4.117)
where µ > 0 is such that B
α
−1
(η)
(0) ⊂ D for some η > β(µ). Then the
nonlinear dynamical system (4.6) and (4.7) is ultimately bounded with
respect to x
1
uniformly in x
2
with bound ε
△
= α
−1
(η). Furthermore,
lim sup
t→∞
kx
1
(t)k ≤ α
−1
(β(µ)). If, in addition, D = R
n
1
and α(·) is a
class K
∞
function, then the nonlinear dynamical system (4.6) and (4.7) is
globally ultimately bounded with respect to x
1
uniformly in x
2
with bound
ε.
Proof. First, let δ ∈ (0, µ] an d assume kx
10
k ≤ δ. As in the proof of
Theorem 4.13, it follows that kx
1
(t)k ≤ α
−1
(η) = ε, t ≥ 0. Next, let δ ∈
(µ, γ), where γ
△
= sup{r > 0 : B
α
−1
(β(r))
(0) ⊂ D} and assume x
10
∈ B
δ
(0)
NonlinearBook10pt November 20, 2007
ADVANCED STABILITY THEORY 239
and kx
10
k > µ. In this case, it follows from Theorem 4.13 that kx
1
(t)k ≤
α
−1
(β(δ)), t ≥ 0. Suppose, ad absurdum, that kx
1
(t)k ≥ β
−1
(η), t ≥ 0,
or, equivalently, x
1
(t) ∈ O
△
= B
α
−1
(β(δ))
(0) \ B
β
−1
(η)
(0), t ≥ 0. Since O is
compact and W (·) is continuous and W (x
1
) > 0, kx
1
k ≥ β
−1
(η) > µ, it
follows from Theorem 2.13 that k
△
= min
x
1
∈O
W (x
1
) > 0 exists. Hence, it
follows from (4.117) that
V (x
1
(t), x
2
(t)) ≤ V (x
10
, x
20
) −kt, t ≥ 0, (4.118)
which implies that
α(kx
1
(t)k) ≤ β(kx
10
k) − kt ≤ β(δ) − kt, t ≥ 0. (4.119)
Now, letting t > β(δ)/k it follows that α(kx
1
(t)k) < 0, which is a contradic-
tion. Hence, th ere exists T = T (δ, η) > 0 such that kx
1
(T )k < β
−1
(η). Thus,
it follows from Theorem 4.13 that kx
1
(t)k ≤ α
−1
(β(β
−1
(η))) = α
−1
(η),
t ≥ T , wh ich proves that the nonlinear dynamical system (4.6) an d (4.7)
is ultimately bounded with respect to x
1
uniformly in x
2
with bound
ε = α
−1
(η). Furtherm ore, lim sup
t→∞
kx
1
(t)k ≤ α
−1
(β(µ)). Finally, if
D = R
n
1
and α(·) is a class K
∞
function it follows that β(·) is a class K
∞
function, and hence, γ = ∞. Hence, the nonlinear dynamical system (4.6)
and (4.7) is globally ultimately bounded with respect to x
1
uniformly in x
2
with bound ε.
Next, we specialize Theorems 4.13 and 4.14 to nonlinear time-varying
dynamical systems. The following definition is needed for these results.
Definition 4.4. i) The nonlinear time-varying dynamical system (4.57)
is Lagrange stable if, for every x
0
∈ R
n
and t
0
∈ R, there exists ε =
ε(t
0
, x
0
) > 0 such that kx(t)k < ε, t ≥ t
0
.
ii) The n on linear time-varying dynamical system (4.57) is uniformly
bounded if there exists γ > 0 such that, for every δ ∈ (0, γ), th ere exists
ε = ε(δ) > 0 such that kx
0
k < δ implies kx(t)k < ε, t ≥ t
0
. The nonlinear
time-varying dynamical system (4.57) is g lobally uniformly bounded if, for
every δ ∈ (0, ∞), there exists ε = ε(δ) > 0 such that kx
0
k < δ imp lies
kx(t)k < ε, t ≥ t
0
.
iii) The nonlinear time-varying dynamical system (4.57) is uniformly
ultimately bounded with bound ε if there exists γ > 0 s uch that, for every δ ∈
(0, γ), th ere exists T = T (δ, ε) > 0 such that kx
0
k < δ implies kx(t)k < ε,
t ≥ t
0
+ T . The nonlinear time-varying dynamical system (4.57) is globally
uniformly ultimately bounded with bound ε if, for every δ ∈ (0, ∞), there
exists T = T (δ, ε) > 0 such that kx
0
k < δ implies kx(t)k < ε, t ≥ t
0
+ T .

NonlinearBook10pt November 20, 2007
240 CHAPTER 4
For the following result define
˙
V (t, x)
△
=
∂V
∂t
+
∂V
∂x
(t, x)f(t, x),
where V : R × D → R is a given continuously differentiable function.
Corollary 4.1. Consider the nonlinear time-varying dynamical system
(4.57). Assume that there exist a continuously differentiable function V :
R ×D → R and class K functions α(·), β(·) such that
α(kxk) ≤ V (t, x) ≤ β(kxk), x ∈ D, t ∈ R, (4.120)
˙
V (t, x) ≤ 0, x ∈ D, kxk ≥ µ, t ∈ R, (4.121)
where µ > 0 is such that B
α
−1
(η)
(0) ⊂ D for some η ≥ β(µ). Then the
nonlinear time-varying dynamical system (4.57) is un iformly boun ded. If,
in addition, D = R
n
and α(·) is a class K
∞
function, then the nonlinear
time-varying dynamical system (4.57) is globally uniformly bounded.
Proof. The result is a direct consequence of Theorem 4.13. Specifi-
cally, let n
1
= n, n
2
= 1, x
1
(t−t
0
) = x(t), x
2
(t−t
0
) = t, f
1
(x
1
, x
2
) = f(t, x),
and f
2
(x
1
, x
2
) = 1. Now, note that with τ = t − t
0
, the solution x(t),
t ≥ t
0
, to the nonlinear time-varying dynamical system (4.57) is equivalently
characterized by the solution x
1
(τ), τ ≥ 0, to the nonlinear autonomous
dynamical system
˙x
1
(τ) = f
1
(x
1
(τ), x
2
(τ)), x
1
(0) = x
0
, τ ≥ 0,
˙x
2
(τ) = 1, x
2
(0) = t
0
,
where ˙x
1
(·) and ˙x
2
(·) denote differentiation with respect to τ . Now, the
result is a direct consequence of Theorem 4.13.
Corollary 4.2. Consider the nonlinear time-varying dynamical system
(4.57). Assu me that there exist a continuously differentiable fun ction V : R×
D → R and class K functions α(·), β(·) such that (4.120) holds. Furthermore,
assume th at there exists a continuous function W : D → R such that W (x) >
0, kxk > µ, and
˙
V (t, x) ≤ −W (x), x ∈ D, kxk > µ, t ∈ R, (4.122)
where µ > 0 is such that B
α
−1
(η)
(0) ⊂ D for some η > β(µ). Then
the nonlinear time-varying dynamical system (4.57) is uniformly ultimately
bounded with bound ε
△
= α
−1
(η). Furthermore, lim su p
t→∞
kx(t)k ≤
α
−1
(β(µ)). If , in addition, D = R
n
and α(·) is a class K
∞
function, then
the nonlinear time-varying dynamical system (4.57) is globally uniformly
ultimately bounded with bound ε.
Proof. The proof is a direct consequence of Theorem 4.14 using similar

NonlinearBook10pt November 20, 2007
ADVANCED STABILITY THEORY 241
arguments as in the proof of Corollary 4.1 and, hence, is omitted.
Finally, we specialize Corollaries 4.1 and 4.2 to nonlinear time-
invariant dynamical systems. For these resu lts we need the f ollowing
specialization of Definition 4.4.
Definition 4.5. i) The nonlinear dynamical system (3.1) is Lagrange
stable if, for every x
0
∈ R
n
, there exists ε = ε(x
0
) > 0 such that kx(t)k < ε,
t ≥ 0.
ii) The nonlinear dynamical system (3.1) is bounded if there exists
γ > 0 such that, for every δ ∈ (0, γ), there exists ε = ε(δ) > 0 such that
kx
0
k < δ implies kx(t)k < ε, t ≥ 0. The nonlinear dynamical system (3.1)
is globally bounded if, for every δ ∈ (0, ∞), there exists ε = ε(δ) > 0 such
that kx
0
k < δ implies kx(t)k < ε, t ≥ 0.
iii) The nonlinear dynamical system (3.1) is ultimately bounded with
bound ε if there exists γ > 0 such that, for every δ ∈ (0, γ), there exists
T = T (δ, ε) > 0 such that kx
0
k < δ implies kx(t)k < ε, t ≥ T . The
nonlinear dynamical system (3.1) is globally ultimately bounded with bound
ε if, for every δ ∈ (0, ∞), there exists T = T (δ, ε) > 0 s uch that kx
0
k < δ
implies kx(t)k < ε, t ≥ T .
Corollary 4.3. Consider th e nonlinear dynamical system (3.1). As-
sume that there exist a continuously differentiable function V : D → R and
class K functions α(·) and β(·) such that
α(kxk) ≤ V (x) ≤ β(kxk), x ∈ D, (4.123)
V
′
(x)f(x) ≤ 0, x ∈ D, kxk ≥ µ, (4.124)
where µ > 0 is such that B
α
−1
(η)
(0) ⊂ D for some η ≥ β(µ). Then the
nonlinear dynamical system (3.1) is bounded. If, in addition, D = R
n
and
V (x) → ∞ as kxk → ∞, then the nonlinear dynamical system (3.1) is
globally bounded.
Proof. The resu lt is a direct consequence of Corollary 4.1.
Corollary 4.4. Consider th e nonlinear dynamical system (3.1). As-
sume that there exist a continuously differentiable function V : D → R and
class K functions α(·) and β(·) such that (4.123) holds and
V
′
(x)f(x) < 0, x ∈ D, kxk > µ, (4.125)
where µ > 0 is such that B
α
−1
(η)
(0) ⊂ D for some η > β(µ). Then the
nonlinear dynamical system (3.1) is ultimately bounded with bound ε
△
=
α
−1
(η). Furthermore, lim sup
t→∞
kx(t)k ≤ α
−1
(β(µ)). If, in addition, D =

NonlinearBook10pt November 20, 2007
242 CHAPTER 4
R
n
and V (x) → ∞ as kxk → ∞, then the nonlinear dynamical system (3.1)
is globally ultimately bounded with boun d ε.
Proof. The proof is a direct consequence of Corollary 4.2.
Corollaries 4.3 and 4.4 present Lyapunov-like theorems for bounded-
ness and u ltimate boundedness of a nonlinear dynamical system. To further
elucidate these results, consider the nonlinear dynamical system (3.1) and
assume that th ere exist a positive-definite, radially unbounded, continuously
differentiable function V : R
n
→ R and scalar µ > 0 s uch that
˙
V (x) ≤ 0, x ∈ R
n
, kxk ≥ µ, t ≥ 0. (4.126)
Furth ermore, let α(·) and β(·) be class K
∞
functions su ch that
α(kxk) ≤ V (x) ≤ β(kxk), x ∈ R
n
. (4.127)
In this case, it can be shown that the set D
µ
△
= {x ∈ R
n
: V (x) ≤ β(µ)}
is positively invariant. To see this, su ppose, ad absurdum, that there exists
a trajectory x(t), t ≥ 0, such that x(0) ∈ D
µ
and x(T ) 6∈ D
µ
for some
T > 0. Now, note that if x ∈ B
µ
(0), then V (x) ≤ β(kxk) ≤ β(µ). Next,
since x(t), t ≥ 0, is continuous it follows that there exists
ˆ
t > 0 such that
V (x(
ˆ
t)) = β(µ) and x(t) 6∈ D
µ
, t ∈ (
ˆ
t, T ], and hence, kx(t)k > µ, t ∈ (
ˆ
t, T ].
Now, it follows from (4.126) that
β(µ) < V (x(T )) = V (x(
ˆ
t)) +
Z
T
ˆ
t
˙
V (x(t))dt ≤ V (x(
ˆ
t) = β(µ),
which is a contradiction. Hence, if x(0) ∈ D
µ
, then x(t) ∈ D
µ
, t ≥ 0.
Similarly, for δ > µ, if x(0) ∈ B
δ
(0), then it can be s hown that x(t) ∈ D
δ
△
=
{x ∈ R
n
: V (x) ≤ β(δ)}. Next, if x ∈ D
δ
, then α(kxk) ≤ V (x) ≤ β(δ),
which implies that x ∈ B
ε
(0), where ε
△
= α
−1
(β(δ)). Hence, if x(0) ∈ B
δ
(0),
then x(t) ∈ B
ε
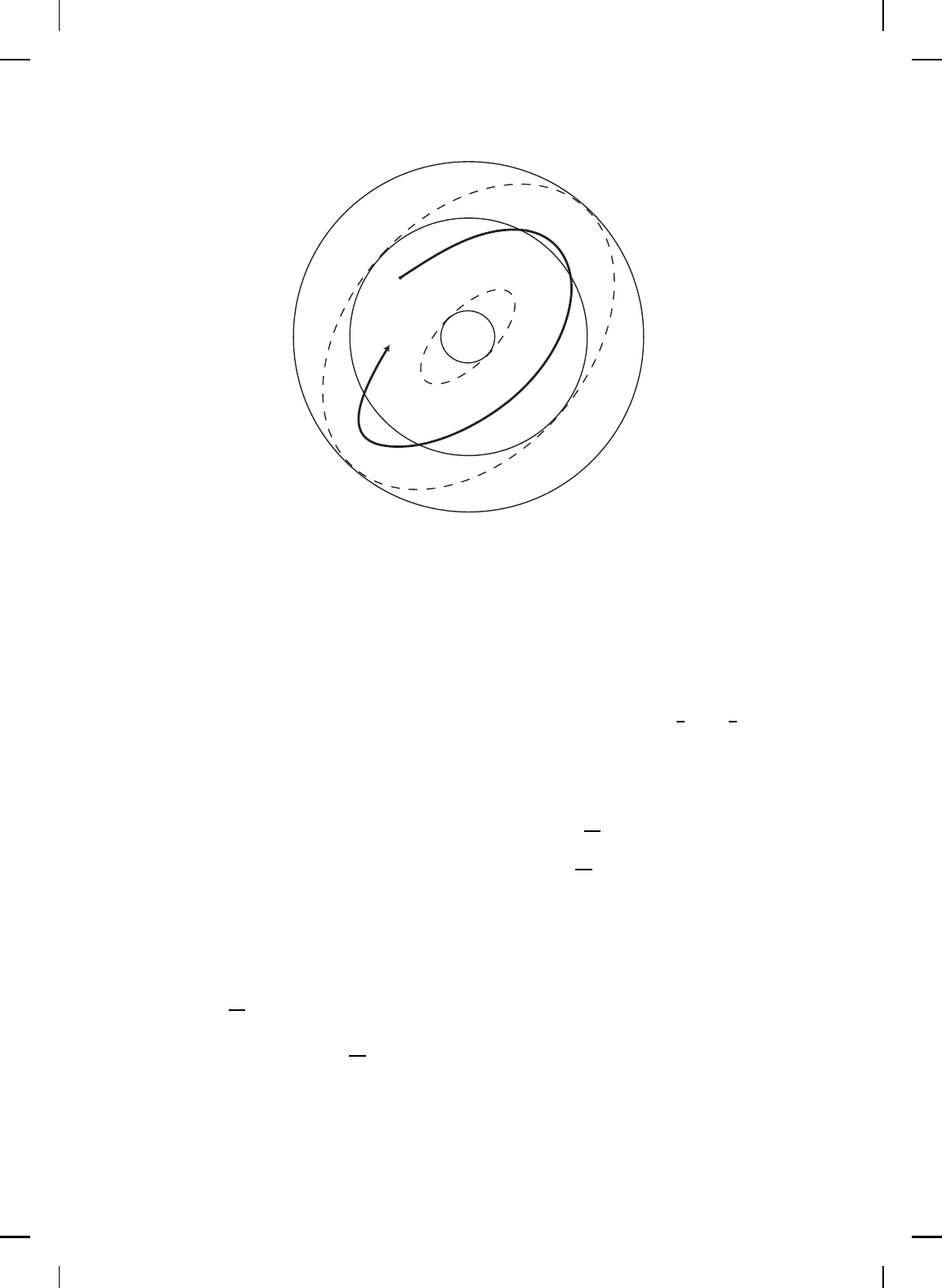
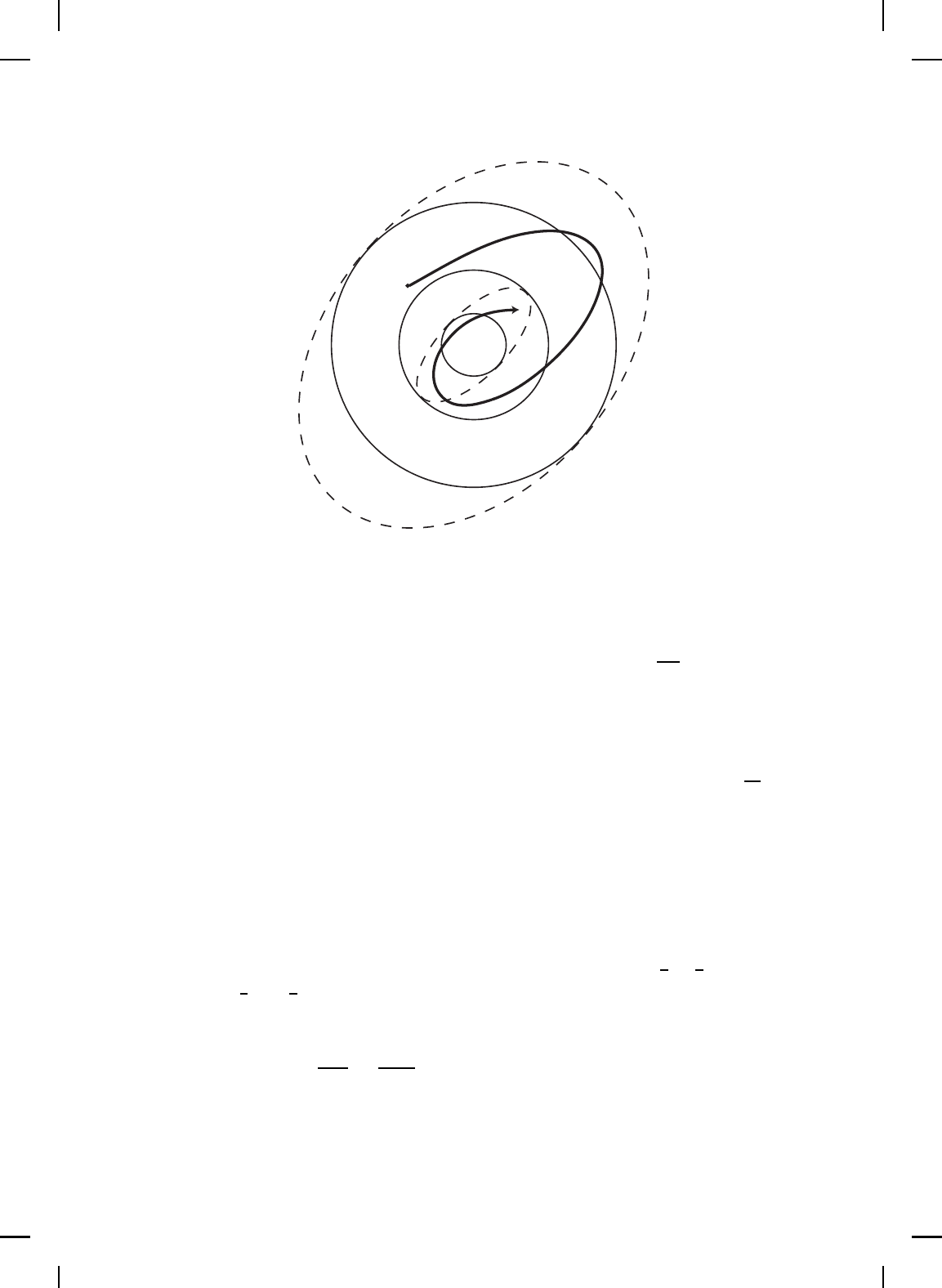
(0), t ≥ 0 (see Figure 4.6).
If (4.126) is replaced by
˙
V (x) < 0, x ∈ R
n
, kxk > µ, t ≥ 0, (4.128)
then, using identical arguments as above, it can be shown that if x(0) ∈
B
δ
(0), then x(t) ∈ D
δ
(0), t ≥ 0. Furthermore, it can be shown that for
every η > µ, the trajectory starting in B
δ
(0) enters D
η
△
= {x ∈ R
n
: V (x) ≤
β(η)} in finite time. Hence, the trajectory either enters D
µ
in finite time
or approaches D
µ
as t → ∞, which, sin ce D
µ
is positively invariant, implies
that the trajectory ultimately enters B
ε
(0), where ε
△
= α
−1
(β(µ)) (see Figure
4.7).
NonlinearBook10pt November 20, 2007
ADVANCED STABILITY THEORY 243
B
ε
(0)
D
δ
B
δ
(0)
x
0
D
µ
B
µ
(0)
Figure 4.6 Visualizations of the sets B
µ
(0) ⊂ D
µ
⊂ B
δ
(0) ⊂ D
δ
⊂ D
ε
and a bounded
trajectory.
Example 4.9. Consider the nonlinear d ynamical system
˙x
1
(t) = −x
1
(t) + x
2
2
(t), x
1
(0) = x
10
, t ≥ 0, (4.129)
˙x
2
(t) = −x
2
(t) + u, x
2
(0) = x
20
, (4.130)
where u ∈ R. To show that (4.129) and (4.130) is globally bounded consider
the radially unbounded, positive definite function V (x
1
, x
2
) =
1
2
x
2
1
+
k
4
x
4
2
,
k > 0, and note that
˙
V (x
1
, x
2
) = −x
1
(−x
1
+ x
2
2
) + kx
3
2
(−x
2
+ u)
= −x
2
1
+ x
1
x
2
2
− k(1 − ε)x
4
2
− kεx
4
2
+ kx
3
2
u, ε ∈ (0, 1),
≤ −x
2
1
+ x
1
x
2
2
− k(1 − ε)x
4
2
, |x
2
| ≥
|u|
ε
,
≤ −
x
1
x
2
2
R
1
x
1
x
2
2
, |x
2
| ≥
|u|
ε
, (4.131)
where
R
1
=
1 −1/2
−1/2 k(1 − ε)
.
Now, choosing k ≥ 1/4(1−ε) ensures that R
1
≥ 0, and hen ce,
˙
V (x
1
, x
2
) ≤ 0,
|x
2
| ≥
|u|
ε
.
Next, for |x
2
| ≤
|u|
ε
, it follows that
˙
V (x
1
, x
2
) ≤ −x
2
1
+ x
1
x
2
2
− kx
4
2
+ k|u|
4
/ε
3
NonlinearBook10pt November 20, 2007
244 CHAPTER 4
B
ε
(0)
D
δ
B
δ
(0)
x
0
D
µ
B
µ
(0)
Figure 4.7 Visualizations of the sets B
µ
(0) ⊂ D
µ
⊂ B
ε
(0) ⊂ B
δ
(0) ⊂ D
δ
and an ultimate
bounded t rajectory.
= −(1 −ε)x
2
1
+ x
1
x
2
2
−kx
4
2
− εx
2
1
+ k|u|
4
/ε
3
≤ −
x
1
x
2
2
R
2
x
1
x
2
2
, |x
1
| ≥ k
1/2
|u|
2
ε
2
, (4.132)
where
R
2
=
1 −ε −1/2
−1/2 k
.
Note that with k ≥ 1/4(1 −ε), R
2
≥ 0, and hence,
˙
V (x
1
, x
2
) ≤ 0, |x
2
| ≤
|u|
ε
.
Next, let δ = min{λ
min
(R
1
), λ
min
(R
2
)} and note that (4.131) and (4.132)
imply
˙
V (x
1
, x
2
) ≤ −δ(x
2
1
+ x
4
2
), kxk
∞
≥ k
1/2
|u|
2
/ε
2
, and h en ce, it follows
from Corollary 4.3 that (4.129) and (4.130) is globally bounded.
Next, to show that (4.129) and (4.130) is globally ultimately bounded,
choose k > 1/4(1 − ε) so that δ > 0. Now, with W (x) = δ(x
2
1
+ x
4
2
),
α(θ) = min
kxk
∞
= θ
V (x), β(θ) = max
kxk
∞
= θ
V (x), and η > β(k
1/2
|u|
2
/ε
2
),
it follows from Corollary 4.4 that (4.129) and (4.130) is globally ultimately
bounded with bound α
−1
(η). Next, n ote that α(θ) = min{
1
2
θ
2
,
k
2
θ
4
} and
β(θ) =
1
2
θ
2
+
k
2
θ
4
, which implies that
α
−1
(β(k
1/2
|u|
2
/ε
2
)) = max{γ
1/2
(|u|), (γ(|u|)/k)
1/4
},
where γ(|u|)
△
=
k|u|
4
ε
4
+
k
3
|u|
8
ε
8
. Now, it f ollows from Corollary 4.4 that
lim sup
t→∞
kx(t)k
∞
≤ max{γ
1/2
(|u|), (γ(|u|)/k)
1/4
}, which implies that,
