Haddad W.M. Nonlinear Dynamical Systems and Control: A Lyapunov-Based Approach

Подождите немного. Документ загружается.

NonlinearBook10pt November 20, 2007

ADVANCED STABILITY THEORY 255

Note that by construction, x(·) is continuously diﬀerentiable on R

\{T (x

)}

and satisﬁes (4.177) on R

\{T (x

)}. Furthermore, since f (·) is continuous,

lim

t→T (x

)

−

˙x(t) = lim

t→T (x

)

−

f(x(t)) = 0 = lim

t→T (x

)

˙x(t), (4.183)

and hence, x(·) is continuously diﬀerentiable at T (x

) and x(·) satisﬁes

(4.177). Hence, x(·) is a solution of (4.177) on R

To show uniqueness, assume y(·) is a solution of (4.177) on R

satisfying y(0) = x

. I n this case, x(·) and y(·) agree on [0, T (x

)),

and by continuity, x(·) and y(·) must also agree on [0, T (x

)], and hence,

y(T (x

)) = 0. Now, Lyapunov stability implies that y(t) = 0 for t > T (x),

which proves uniqueness. Finally, by deﬁnition, s

(t) = x(t), and hence,

(·) is deﬁned on R

and satisﬁes s

(t) = 0 on [T (x

), ∞) for every

∈ N. This proves the result.

It follows f rom Proposition 4.5 that if the zero solution x(t) ≡ 0 to

(4.177) is ﬁnite-time stable, then the solutions of (4.177) deﬁne a continuous

global semiﬂow on N; that is, s : R

× N → N is jointly continuous and

satisﬁes s(0, x) = x and s(t, s(τ, x)) = s(t + τ, x) for every x ∈ N and

t, τ ∈ R

. Furthermore, s(·, ·) satisﬁes s(T (x) + t, x) = 0 for all x ∈ N and

t ∈ R

. Finally, it also follows f rom Proposition 4.5 that we can extend T (·)

to all of N by d eﬁ ning T (0) , 0. It is easy to see from Deﬁnition 4.7 that

T (x) = inf{t ∈ R

: s(t, x) = 0}, x ∈ N. (4.184)

The following example adopted from [55] presents a ﬁnite-time stable

system with a continuous but non-Lips chitzian vector ﬁeld.

Example 4.12. Consider the scalar nonlinear dynamical system given

˙x(t) = −k sign(x(t))|x(t)|

, x(0) = x

, t ≥ 0, (4.185)

where x

∈ R, s ign(x)

△

|x|

, x 6= 0, sign(0)

△

= 0, k > 0, and α ∈ (0, 1). The

right-hand side of (4.185) is continuous everywhere and locally Lipschitz

everywhere except the origin. Hence, every initial condition in R\{0} has

a unique solution in forward time on a suﬃciently small time interval. The

solution to (4.185) is obtained by d ir ect integration and is given by

s(t, x

)











sign(x

)



1−α

− k(1 −α)t



1−α

, t <

k(1−α)

1−α

, x

6= 0,

0, t ≥

k(1−α)

1−α

, x

6= 0,

0, t ≥ 0, x

= 0.

(4.186)

NonlinearBook10pt November 20, 2007

256 CHAPTER 4

It is clear from (4.186) that i) in Deﬁnition 4.7 is satisﬁed with N = D = R

and with the settling-time function T : R → R

given by

T (x

) =

k(1 −α)

1−α

, x

∈ R. (4.187)

Lyapunov stability follows by considering th e Lyapunov function V (x) = x

x ∈ R. Thus, the zero solution x(t) ≡ 0 to (4.185) is globally ﬁn ite-time

stable. △

The next proposition shows that the settling-time function of a ﬁnite-

time stable system is continuous on N if and only if it is continuous at the

origin.

Proposition 4.6. Consider the nonlinear dynamical s ystem (4.177).

Assume that the zero solution x(t) ≡ 0 to (4.177) is ﬁ nite-time stable, let

N ⊆ D be as in Deﬁnition 4.7, and let T : N → R

be the settling-time

function. Then T (·) is continuous on N if and only if T (·) is continuous at

x = 0.

Proof. Necessity is immediate. To show suﬃciency, suppose T (·) is

continuous at x = 0, let y ∈ N, and consider the sequence {y

}

∞

n=0

in N

converging to y. Let τ

−

= lim inf

n→∞

T (y

) and τ

= lim sup

n→∞

T (y

Note that τ

−

, τ

∈ R

and

−

≤ τ

. (4.188)

Next, let {y

}

∞

m=0

be a subsequ en ce of {y

}

∞

n=0

such that T (y

) → τ

as m → ∞. The sequ en ce {T (y), y

}

∞

m=0

converges in R

×N to (T (y), y).

Now, it follows from continuity and s(T (x) + t, x) = 0 for all x ∈ N and

t ∈ R

that s(T (y), y

) → s(T (y), y) = 0 as m → ∞. Since, by assumption,

T (·) is continuous at x = 0, T (s(T (y), y

)) → T (0) = 0 as m → ∞. Next,

using (4.184), the semigroup property s(t, s(τ, x)) = s(t + τ, x), x ∈ N and

t, τ ∈ R

, and s(T (x) + t, x) = 0, x ∈ N and t, τ ∈ R

, it follows that

T (s(t, x)) = max{T (x) − t, 0}. (4.189)

Now, with t = T (y) and x = y

, it follows from (4.189) th at max{T (y

) −

T (y), 0} → 0 as m → ∞. Hence, max{τ

− T (y), 0} = 0, that is,

≤ T (y). (4.190)

Finally, let {y

−

}

∞

m=0

be a subsequence of {y

}

∞

n=0

such that T (y

−

) →

−

as m → ∞. Now, it follows from (4.188) and (4.190) that τ

−

∈ R

and hence, the sequence {T (y

−

), y

−

}

∞

m=0

converges in R

× N to (τ

−

, y).

Since s(·, ·) is jointly continuous, it follows that s(T (y

−

), y

−

) → s(τ

−

, y) as

m → ∞. Now, s(T (x) + t, x) = 0 for all x ∈ N and t ∈ R

implies that

NonlinearBook10pt November 20, 2007

ADVANCED STABILITY THEORY 257

s(T (y

−

), y

−

) = 0 for each m. Hence, s(τ

−

, y) = 0 and, by (4.184),

T (y) ≤ τ

−

. (4.191)

Now, it follows from (4.188), (4.190), and (4.191) that τ

−

= τ

= T (y), and

hence, T (y

) → T (y) as n → ∞, which proves that T (·) is continuous on

Next, we present suﬃcient conditions for ﬁ nite-time stability using a

Lyapunov function involving a scalar diﬀerential inequality.

Theorem 4.17. Consider the nonlinear dynamical system (4.177).

Assume there exist a continuously diﬀerentiable f unction V : D → R

real numbers c > 0 and α ∈ (0, 1), and a neighborhood M ⊆ D of the origin

such that

V (0) = 0, (4.192)

V (x) > 0, x ∈ M\{0}, (4.193)

′

(x)f(x) ≤ −c(V (x))

, x ∈ M\{0}. (4.194)

Then the zero solution x(t) ≡ 0 to (4.177) is ﬁnite-time stable. Moreover,

there exist an open neighborhood N of the origin and a settling-time function

T : N → [0, ∞) such that

T (x

) ≤

c(1 −α)

(V (x

))

1−α

, x

∈ N, (4.195)

and T (·) is continuous on N. If, in addition, D = R

, V (·) is radially

unbounded, and (4.194) holds on R

, th en the zero s olution x(t) ≡ 0 to

(4.177) is globally ﬁnite-time stable.

Proof. Since V (·) is positive deﬁnite and

V (·) takes negative values

on M\{0}, it follows that x(t) ≡ 0 is the unique solution of (4.177) for t ≥ 0

satisfying x(0) = 0 [4, Section 3.15], [474, Theorem 1.2, p. 5]. Thus, for

every initial condition in D, (4.177) has a unique solution in forward time.

Let V ⊆ M be a bounded open set such that 0 ∈ V and V ⊂ D.

Then ∂V is compact and 0 6∈ ∂V. Now, it follows from Weierstrass’ theorem

(Theorem 2.13) that the continuous function V (·) attains a minimum on

∂V and since V (·) is positive deﬁnite, min

x∈∂V

V (x) > 0. Let 0 < β <

min

x∈∂V

V (x) and D

△

= {x ∈ V : V (x) ≤ β}. It follows from (4.194)

that D

⊂ M is positively invariant with respect to (4.177). Furthermore,

it follows from (4.194), the positive deﬁniteness of V (·), and standard

Lyapunov arguments that, for every ε > 0, there exists δ > 0 such that

(0) ⊂ D

⊂ M and

kx(t)k ≤ ε, kx

k < δ, t ∈ I

. (4.196)

NonlinearBook10pt November 20, 2007

258 CHAPTER 4

Moreover, since the solution x(t) to (4.177) is bounded for all t ∈ I

, it can

be extended on the semi-inﬁnite interval [0, ∞), and hence, x(t) is deﬁned

for all t ≥ 0. Furthermore, it follows from Theorem 4.16, with w(y) = −cy

and z(t) = s(t, V (x

)), where α ∈ (0, 1), that

V (x(t)) ≤ s(t, V (x

)), x

∈ B

(0), t ∈ [0, ∞), (4.197)

where s(·, ·) is given by (4.186) with k = c. Now, it follows from (4.186),

(4.197), and the positive deﬁniteness of V (·) that

x(t) = 0, t ≥

c(1 − α)

(V (x

))

1−α

, x

∈ B

(0), (4.198)

which implies ﬁnite-time convergence of the trajectories of (4.177) for all

∈ B

(0). This along with (4.196) imp lies ﬁnite-time stability of the zero

solution x(t) ≡ 0 to (4.177) with N

△

= B

(0).

Since s(0, x) = x and s(·, ·) is continuous, inf{t ∈ R

: s(t, x) = 0} > 0,

x ∈ N\{0}. Furthermore, it follows from (4.198) that inf{t ∈ R

: s(t, x) =

0} < ∞, x ∈ N. Now, deﬁning T : N → R

by using (4.184), (4.195) is

immediate from (4.198). Finally, the right-hand side of (4.195) is continuous

at the origin, and hence, by Pr oposition 4.6, continuous on N.

Finally, if D = R

and V (·) is radially unbounded, then global ﬁnite-

time stability follows using standard arguments.

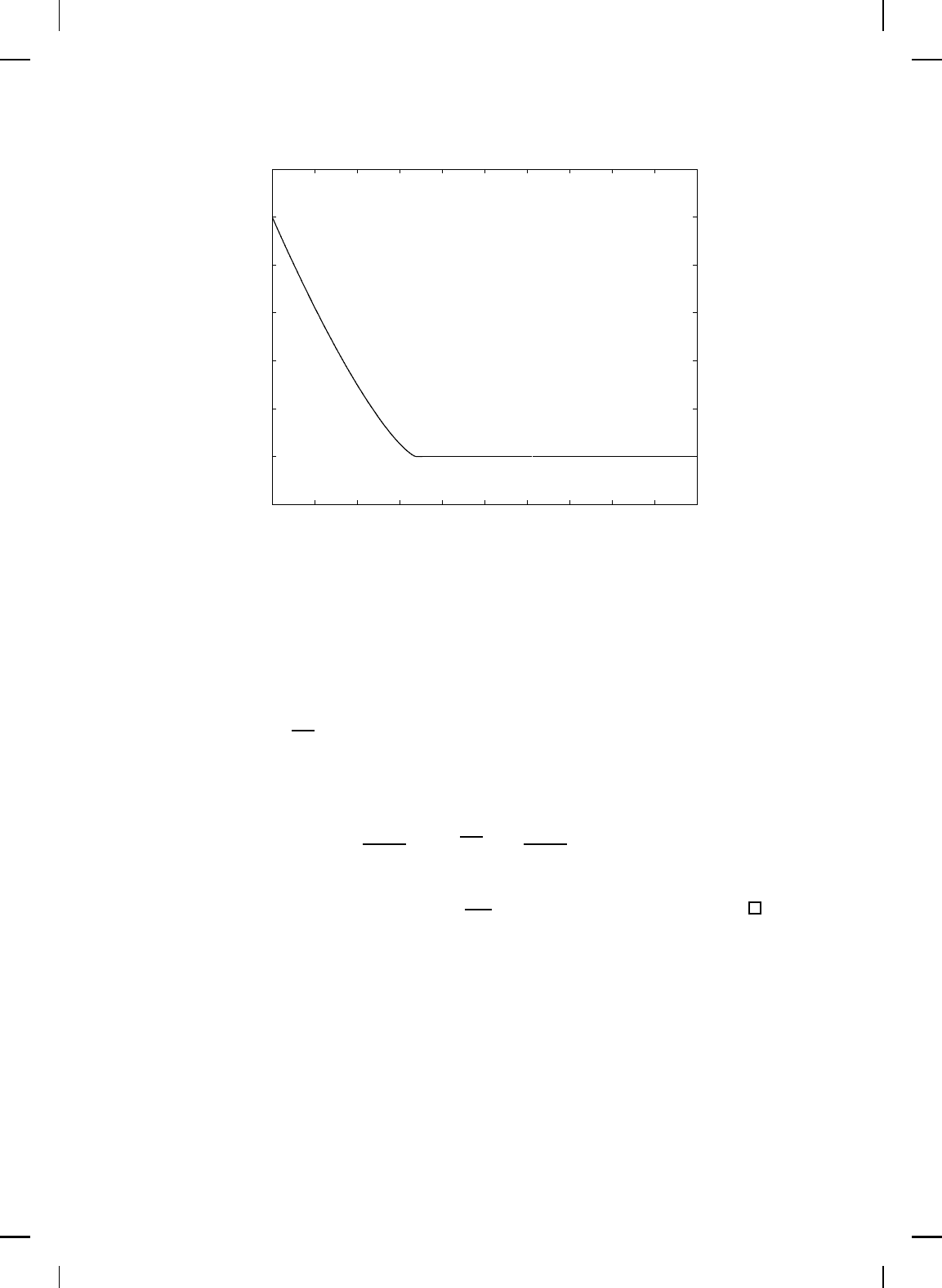
Example 4.13. Consider the nonlinear d y namical system G given by

˙x(t) = −(x(t))

− (x(t))

, x(0) = x

, t ≥ 0, (4.199)

where x ∈ R. For this system, we show that the zero solution x(t) ≡ 0 to

(4.199) is globally ﬁnite-time stable. To see this, consider V (x) = x

and

let D = R. Then,

V (x) = −

+ x

) ≤ −

= −

(V (x))

for all

x ∈ R. Hence, it follows from Theorem 4.17 that the zero solution x(t) ≡ 0

to (4.199) is globally ﬁnite-time stable. Figure 4.8 shows the state trajectory

versus time of G with x

= 1. △

Finally, we present a converse theorem for ﬁnite-time stability in the

case where the settling-time function is continuous. For the statement of

this result, deﬁne

V (x) , lim

h→0

[V (s(h, x)) − V (x)], x ∈ D, (4.200)

for a given continuous function V : D → R and for every x ∈ D such th at

the limit in (4.200) exists.

Theorem 4.18. Let α ∈ (0, 1) and let N be as in Deﬁnition 4.7. If the

zero solution x(t) ≡ 0 to (4.177) is ﬁnite-time stable and the settling-time

NonlinearBook10pt November 20, 2007

ADVANCED STABILITY THEORY 259

0 0.2 0.4 0.6 0.8 1 1.2 1.4 1.6 1.8 2

−0.2

0.2

0.4

0.6

0.8

1.2

Time

State

Figure 4.8 State trajectory versus time for Example 4.13.

function T (·) is continuous at x = 0, then there exist a continuous function

V : N → R and a scalar c > 0 such that V (0) = 0, V (x) > 0, x ∈ N, x 6= 0,

and

V (x) ≤ −c(V (x))

, x ∈ N.

Proof. First, it follows from Proposition 4.6 that the s ettling-time

function T : N → R

is continuous. Next, deﬁne V : N → R

V (x) = (T (x))

1−α

. Note that V (·) is continuous and positive deﬁnite and,

by s(T (x) + t, x) = 0 for all x ∈ N and t ∈ R

V (0) = 0. Now, (4.189)

implies that V (s

(t)) is continuously diﬀerentiable on [0, T (x)), and hence,

(4.200) yields

V (x) = −

1 −α

(T (x))

1−α

= −

1 −α

(V (x))

. (4.201)

Hence,

V (·) is continuous and negative deﬁnite on N and satisﬁes

V (x) +

c(V (x))

= 0 for all x ∈ N w ith c =

1−α

4.7 Semistability of Nonlinear Dynamical Systems

In this section, we develop a stability analysis framework for systems having

a continuum of equilibria. Since every neighborhood of a nonisolated

equilibrium contains another equilibrium, a nonisolated equilibrium cannot

be asymptotically stable. Hence, asymptotic stability is not the appropriate

notion of stability for systems having a continuum of equilibria. Two

NonlinearBook10pt November 20, 2007

260 CHAPTER 4

notions that are of particular r elevance to such systems are convergence and

semistability. Convergence is the property wh ereby every system solution

converges to a limit point that may depend on the system initial cond ition.

Semistability is the additional r equ irement that all solutions converge to

limit points that are Lyapun ov stable. Semistability for an equilibriu m thus

implies Lyapunov stability, and is implied by asymptotic stability.

It is important to note that semistability is not merely equivalent to

asymptotic stability of the set of equilibria. Indeed, it is possible for a

trajectory to converge to the set of equilibria without converging to any

one equilibrium point (see Problem 4.32). Conversely, semistability does

not imply th at the equilibrium set is asymptotically stable in any accepted

sense. This is because stability of sets (see Section 4.9) is deﬁned in terms

of distance (especially in case of noncompact sets), and it is possible to

construct examples in which the dynamical system is s emistable, but the

domain of semistability (see Deﬁnition 4.9) contains no ε-neighborhood

(deﬁned in terms of the distance) of the (noncompact) equilibrium set, thus

ruling out asymptotic stability of the equilibrium set. Hence, semistability

and set stability of the equilibrium set are in dependent notions.

The dependen ce of the limiting state on the initial state is seen

in numerous dynamical systems including compartmental systems [220]

which arise in chemical kinetics [47], biomedical [219], environmental [338],

economic [40], power [400], and thermodynamic sys tems [167]. For these

systems, every trajectory that starts in a n eighborhood of a Lyapunov stable

equilibrium converges to a (possibly diﬀerent) Lyapun ov stable equilibrium,

and hence these systems are semistable. Semistability is es pecially pertinent

to networks of dyn amic agents which exhibit convergence to a state of

consensus in which the agents agree on certain quantities of interest [208].

Semistability was ﬁrst introduced in [81] for linear systems, and applied

to matrix second-order systems in [46]. References [57] and [56] consider

semistability of nonlinear systems, and give several stability results for

systems having a continuum of equilibria based on nontangency and arc

length of trajectories, respectively.

In this section, we develop necessary and suﬃcient conditions for

semistability. Speciﬁcally, we consider nonlinear dynamical systems G of

the form

˙x(t) = f (x(t)), x(0) = x

, t ∈ I

, (4.202)

where x(t) ∈ D ⊆ R

, t ∈ I

, is the system state vector, D is an open set,

f : D → R

is Lipschitz continuous on D, f

−1

(0) , {x ∈ D : f (x) = 0}

is nonempty, and I

= [0, τ

), 0 ≤ τ

≤ ∞, is the maximal interval of

existence for th e solution x(·) of (4.202). Here, we assume that for every

NonlinearBook10pt November 20, 2007

ADVANCED STABILITY THEORY 261

initial condition x

∈ D, (4.202) has a unique solution deﬁned on [0, ∞),

and hence, the solutions of (4.202) deﬁne a continuous global semiﬂow on

D. We say that the dynamical system (4.202) is convergent with respect to

the closed set D

⊆ D if lim

t→∞

s(t, x) exists for every x ∈ D

The following proposition gives a suﬃcient cond ition f or a trajectory

of (4.202) to converge to a limit. For this result, D

⊆ D denotes a positively

invariant set with respect to (4.202) so that the orbit O

of (4.202) is

contained in D

for all x ∈ D

Proposition 4.7. Consider the nonlinear d ynamical system (4.202)

and let x ∈ D

. If the positive orbit O

of (4.202) contains a Lyapunov

stable equilibrium point y, then y = lim

t→∞

s(t, x), that is, O

= {y}.

Proof. Suppose y ∈ O

is Lyapunov stable and let N

⊆ D

an open neighborhood of y. Since y is Lyapunov stable, there exists an

open neighborhood N

⊂ D

of y such that s

) ⊆ N

for every t ≥ 0.

Now, since y ∈ O

, it follows that there exists τ ≥ 0 such that s(τ, x) ∈ N

Hence, s(t+τ, x) = s

(s(τ, x)) ∈ s

) ⊆ N

for every t > 0. Since N

⊆ D

is arbitrary, it follows that y = lim

t→∞

s(t, x). Thus, lim

n→∞

s(t

, x) = y

for every sequence {t

}

∞

n=1

, and hence, O

= {y}.

The following deﬁnitions and key proposition are necessary for the

main results of this section.

Deﬁnition 4.8. An equilibrium point x ∈ D of (4.202) is Lyapunov

stable if for every open subset N

of D containing x, there exists an open

subset N

of D containing x such that s

) ⊂ N

for all t ≥ 0. An

equilibrium point x ∈ D of (4.202) is semistable if it is Lyapunov stable

and there exists an open subset Q of D containin g x such that for all

initial conditions in Q, the trajectory of (4.202) converges to a Lyapunov

stable equilibrium point, that is, lim

t→∞

s(t, x) = y, where y ∈ D is a

Lyapunov stable equ ilibr ium point of (4.202) and x ∈ Q. I f, in addition,

Q = D = R

, then an equilibrium point x ∈ D of (4.202) is a globally

semistable equilibrium. T he system (4.202) is said to be Lyapunov stable if

every equilibrium point of (4.202) is Lyapunov stable. The system (4.202)

is said to be semistable if every equilibrium point of (4.202) is semistable.

Finally, (4.202) is said to be globally semistable if (4.202) is s emistable and

Q = D = R

Deﬁnition 4. 9. The domain of semistability is the set of points x

∈ D

such that if x(t) is a solution to (4.202) with x(0) = x

, t ≥ 0, then x(t)

converges to a Lyapunov stable equilibr ium point in D.

Note that if (4.202) is semistable, then its domain of semistability

NonlinearBook10pt November 20, 2007

262 CHAPTER 4

contains the set of equilibria in its interior. Next, we present alternative

equivalent characterizations of semistability of (4.202).

Proposition 4.8. Consider the nonlinear dy namical system G given by

(4.202). Then the following statements are equivalent:

i) G is semistable.

ii) For each x

∈ f

−1

(0), there exist class K and L functions α(·) and

β(·), respectively, and δ = δ(x

) > 0, such that if kx

− x

k < δ, then

kx(t) −x

k ≤ α(kx

−x

k), t ≥ 0, and dist(x(t), f

−1

(0)) ≤ β(t), t ≥ 0.

iii) For each x

∈ f

−1

(0), there exist class K functions α

(·) and α

(·), a

class L function β(·), and δ = δ(x

) > 0, such that if kx

− x

k < δ,

then dist(x(t), f

−1

(0)) ≤ α

(kx(t) − x

k)β(t) ≤ α

(kx

− x

k)β(t),

t ≥ 0.

Proof. To show that i) implies ii), suppose (4.202) is semistable and

let x

∈ f

−1

(0). It follows from Problem 3.75 that there exists δ = δ(x

) > 0

and a class K fun ction α(·) such that if kx

− x

k ≤ δ, then kx(t) − x

k ≤

α(kx

− x

k), t ≥ 0. Without loss of generality, we may assum e that δ

is such that B

) is contained in the domain of semistability of (4.202).

Hence, for every x

∈ B

), lim

t→∞

x(t) = x

∗

∈ f

−1

(0) and, consequently,

lim

t→∞

dist(x(t), f

−1

(0)) = 0.

For each ε > 0 and x

∈ B

), deﬁne T

(ε) to be the inﬁmum

of T with the property that dist(x(t), f

−1

(0)) < ε for all t ≥ T , that is,

(ε) , inf{T : dist(x(t), f

−1

(0)) < ε, t ≥ T }. For each x

∈ B

), th e

function T

(ε) is nonnegative and nonincreasing in ε, and T

(ε) = 0 for

suﬃciently large ε.

Next, let T (ε) , sup{T

(ε) : x

∈ B

)}. We claim that T

is well deﬁned. To show this, consider ε > 0 and x

∈ B

). Since

dist(s(t, x

), f

−1

(0)) < ε for every t > T

(ε), it follows from the continuity

of s that, for every η > 0, there exists an open neighborhood U of x

such

that dist(s(t, z), f

−1

(0)) < ε for every z ∈ U. Hence, lim sup

z→x

(ε) ≤

(ε) implying that the function x

7→ T

(ε) is upper semicontinuous

at the arbitrarily chosen point x

, and hence on B

). Since an u pper

semicontinuous function d eﬁ ned on a compact set achieves its supremum,

it follows that T (ε) is well deﬁned. The function T (·) is th e pointwise

supremum of a collection of nonnegative and nonincreasing functions, and

is hence nonnegative and nonincreasing. Moreover, T (ε) = 0 for every

ε > max{α(kx

− x

k) : x

∈ B

)}.

NonlinearBook10pt November 20, 2007

ADVANCED STABILITY THEORY 263

Let ψ(ε) ,

ε/2

T (σ)d σ +

≥ T (ε) +

. The function ψ(ε) is

positive, continuous, strictly decreasing, and ψ(ε) → 0 as ε → ∞. Choose

β(·) = ψ

−1

(·). Then β(·) is positive, continuous, strictly decreasing, and

β(σ) → 0 as σ → ∞. Furthermore, T (β(σ)) < ψ(β(σ)) = σ. Hence,

dist(x(t), f

−1

(0)) ≤ β(t), t ≥ 0.

Next, to show that ii) implies iii), suppose ii) holds and let x

∈

−1

(0). Then it follows from Problem 3.75 that x

is Lyapunov stable.

Choosing x

suﬃciently close to x

, it follows from th e inequality kx(t) −

k ≤ α(kx

− x

k), t ≥ 0, that trajectories of (4.202) starting suﬃciently

close to x

are bounded, and hence, the positive limit set of (4.202) is

nonempty. Since lim

t→∞

dist(x(t), f

−1

(0)) = 0, it f ollows that the positive

limit set is contained in f

−1

(0). Now, since every point in f

−1

(0) is

Lyapunov stable, it follows from Proposition 4.7 that lim

t→∞

x(t) = x

∗

where x

∗

∈ f

−1

(0) is Lyapunov stable. If x

∗

= x

, then it follows using

similar arguments as above that there exists a class L f unction

β(·) such that

dist(x(t), f

−1

(0)) ≤ kx(t) −x

k ≤

β(t) f or every x

satisfying kx

−x

k < δ

and t ≥ 0. Hence, dist(x(t), f

−1

(0)) ≤

kx(t) − x

β(t), t ≥ 0. Next,

consider the case where x

∗

6= x

and let α

(·) be a class K function. In this

case, note that lim

t→∞

dist(x(t), f

−1

(0))/α

(kx(t) −x

k) = 0, and hence, it

follows us ing similar arguments as above that there exists a class L function

β(·) such that dist(x(t), f

−1

(0)) ≤ α

(kx(t) − x

k)β(t), t ≥ 0. Finally,

note that α

◦ α is of class K (by Problem 3.71), and hence, iii) follows

immediately.

Finally, to show that iii) implies i), suppose iii) holds and let x

∈

−1

(0). Then it follows that α

(kx(t) − x

k) ≤ α

(kx(0) − x

k), t ≥ 0, that

is, kx(t) −x

k ≤ α(kx(0) −x

k), where t ≥ 0 and α = α

−1

◦α

is of class K

(by Problem 3.71). It now f ollows from Problem 3.75 that x

is Lyapunov

stable. Since x

was chosen arbitrarily, it follows that every equilibrium point

is Lyapunov stable. Furthermore, lim

t→∞

dist(x(t), f

−1

(0)) = 0. Choosing

suﬃciently close to x

, it follows from the inequality kx(t)−x

k ≤ α(kx

−

k), t ≥ 0, that trajectories of (4.202) starting suﬃciently close to x

are

bounded, and hence, the positive limit set of (4.202) is nonempty. Since

every point in f

−1

(0) is Lyapunov stable, it follows from Proposition 4.7

that lim

t→∞

x(t) = x

∗

, where x

∗

∈ f

−1

(0) is Lyapunov stable. Hence, by

deﬁnition, (4.202) is semistable.

Next, we present a su ﬃcient condition for semistability.

Theorem 4.19. Consider the nonlinear dynamical system (4.202). Let

Q be an open neighborhood of f

−1

(0) and assume that there exists a

NonlinearBook10pt November 20, 2007

264 CHAPTER 4

continuously diﬀerentiable function V : Q → R such that

′

(x)f(x) < 0, x ∈ Q\f

−1

(0). (4.203)

If (4.202) is Lyapunov stable, then (4.202) is semistable.

Proof. Since (4.202) is Lyapunov stable by assumption, for every

z ∈ f

−1

(0), there exists an open neighborhood V

of z such that s([0, ∞) ×

) is bounded an d contained in Q. The set V ,

z∈f

−1

(0)

is an open

neighborhood of f

−1

(0) contained in Q. Consider x ∈ V so that there

exists z ∈ f

−1

(0) such that x ∈ V

and s(t, x) ∈ V

, t ≥ 0. Since V

bounded it follows that the positive limit set of x is nonempty and invariant.

Furth ermore, it follows f rom (4.203) that

V (s(t, x)) ≤ 0, t ≥ 0, and hence,

it follows from Theorem 3.3 that s(t, x) → M as t → ∞, where M is the

largest invariant set contained in the set R = {y ∈ V

: V

′

(y)f(y) = 0}.

Note that R = f

−1

(0) is invariant, and hence, M = R, which implies

that lim

t→∞

dist(s(t, x), f

−1

(0)) = 0. Finally, since every point in f

−1

(0) is

Lyapunov stable, it follows from Proposition 4.7 that lim

t→∞

s(t, x) = x

∗

where x

∗

∈ f

−1

(0) is Lyapunov stable. Hence, by deﬁnition, (4.202) is

semistable.

Next, we present a slightly more general theorem for s emistability

wherein we do not assume that all points in

−1

(0) are Lyapunov stable but

rather we assume that all points in the largest invariant su bset of

−1

(0)

are Lyapunov stable.

Theorem 4.20. Consider the nonlinear d ynamical system (4.202) and

let Q be an open neighborh ood of f

−1

(0). Sup pose the orbit O

of (4.202)

is bounded for all x ∈ Q and assume that there exists a continuously

diﬀerentiable function V : Q → R such that

′

(x)f(x) ≤ 0, x ∈ Q. (4.204)

If every point in the largest invariant subset M of {x ∈ Q : V

′

(x)f(x) = 0}

is Lyapunov stable, then (4.202) is semistable.

Proof. Since every solution of (4.202) is bounded, it follows from

the hypotheses on V (·) that, for every x ∈ Q, the positive limit set ω(x)

of (4.202) is nonempty and contained in the largest invariant subset M

of {x ∈ Q : V

′

(x)f(x) = 0}. Sin ce every point in M is a Lyapunov s table

equilibrium, it follows from P roposition 4.7 th at ω(x) contains a single point

for every x ∈ Q and lim

t→∞

s(t, x) exists for every x ∈ Q. Now, since

lim

t→∞

s(t, x) ∈ M is Lyapunov stable for every x ∈ Q, semistability is

immediate.