Haddad W.M. Nonlinear Dynamical Systems and Control: A Lyapunov-Based Approach

Подождите немного. Документ загружается.

NonlinearBook10pt November 20, 2007

ADVANCED STABILITY THEORY 225

then the nonlinear dynamical system given by (4.6) and (4.7) is

asymptotically stable with respect to x

uniformly in x

v) If D = R

and there exist continuously diﬀerentiable functions V :

× R

→ R and W : R

× R

→ R, class K functions β(·), γ(·),

and a class K

∞

function α(·) such that

W (x

(·), x

(·)) is bounded from

below or above, and (4.49), (4.52), and (4.53) hold, then the nonlinear

dynamical system given by (4.6) and (4.7) is globally asymptotically

stable with respect to x

vi) If D = R

and there exist a continuously diﬀerentiable function

V : R

× R

→ R, a class K function γ(·), and class K

∞

functions

α(·), β(·) satisfying (4.49), (4.51), and (4.54), then the nonlinear

dynamical system given by (4.6) and (4.7) is globally asymptotically

stable with respect to x

uniformly in x

vii) If there exist a continuously diﬀerentiable function V : D × R

→ R

and positive constants α, β, γ, p ≥ 1 satisfying

αkx

≤ V (x

, x

) ≤ βkxk

, (x

, x

) ∈ D × R

, (4.55)

V (x

, x

) ≤ −γkxk

, (x

, x

) ∈ D × R

, (4.56)

then the nonlinear dynamical system given by (4.6) and (4.7) is

exponentially stable with respect to x

uniformly in x

viii) If D = R

and there exist a continuously diﬀerentiable function V :

× R

→ R and positive constants α, β, γ, p ≥ 1 satisfying (4.55)

and (4.56), then the nonlinear dynamical system given by (4.6) and

(4.7) is globally exponentially stable with respect to x

uniformly in

Proof. The proof is virtually identical to the proof of Theorem 4.1

and is left as an exercise for the reader.

4.3 Stability Theory for Nonlinear Time-Varying Systems

In this section, we use the results of Section 4.2 to extend Lyapunov’s direct

method to nonlinear time-varying systems, thereby providing a uniﬁcation

between partial stability theory for au tonomous systems and stability th eory

for time-varying systems. Speciﬁcally, we consider the nonlinear time-

varying dynamical system

˙x(t) = f(t, x(t)), x(t

) = x

, t ≥ t

, (4.57)

where x(t) ∈ D, t ≥ t

, D ⊆ R

such th at 0 ∈ D, f : [t

, t

) × D → R

such that f (·, ·) is jointly continuous in t and x, and for every t ∈ [t

, t

f(t, 0) = 0 and f(t, ·) is locally Lipschitz in x uniformly in t for all t in

NonlinearBook10pt November 20, 2007

226 CHAPTER 4

compact subsets of [0, ∞). Note that under the above assumptions the

solution x(t), t ≥ t

, to (4.57) exists and is unique over the interval [t

, t

The following deﬁnition provides eight types of stability for the nonlinear

time-varying dynamical system (4.57).

Deﬁnition 4.2. i) The nonlinear time-varying dynamical system (4.57)

is Lyapunov stable if, for every ε > 0 and t

∈ [0, ∞), there exists δ =

δ(ε, t

) > 0 such that kx

k < δ implies that kx(t)k < ε for all t ≥ t

ii) The n on linear time-varying dynamical system (4.57) is u niformly

Lyapunov stable if, for every ε > 0, there exists δ = δ(ε) > 0 such that

k < δ implies that kx(t)k < ε for all t ≥ t

and for all t

∈ [0, ∞).

iii) The nonlinear time-varying dynamical system (4.57) is asymptot-

ically stable if it is Lyapunov stable and for every t

∈ [0, ∞), there exists

δ = δ(t

) > 0 such that kx

k < δ implies that lim

t→∞

x(t) = 0.

iv) The nonlinear time-varying dynamical system (4.57) is uniformly

asymptotically stable if it is uniformly Lyapunov stable and there exists δ > 0

such that kx

k < δ implies that lim

t→∞

x(t) = 0 uniformly in t

and x

for

all t

∈ [0, ∞).

v) The nonlinear time-varying dynamical system (4.57) is globally

asymptotically stable if it is Lyapunov stable and lim

t→∞

x(t) = 0 for all

∈ R

and t

∈ [0, ∞).

vi) The nonlinear time-varying dynamical system (4.57) is globally

uniformly asymptotically stable if it is uniformly Lyapunov stable and

lim

t→∞

x(t) = 0 uniformly in t

and x

for all x

∈ R

and t

∈ [0, ∞).

vii) The nonlinear time-varying dynamical system (4.57) is (uniformly)

exponentially stable if there exist scalars α, β, δ > 0 such that kx

k < δ

implies that kx(t)k ≤ αkx

−βt

, t ≥ t

and t

∈ [0, ∞).

viii) The nonlinear time-varying dynamical system (4.57) is globally

(uniformly) exponentially stable if there exist scalars α, β > 0 such that

kx(t)k ≤ αkx

−βt

, t ≥ t

, for all x

∈ R

and t

∈ [0, ∞).

Note that uniform asymptotic stability is equivalent to uniform

Lyapunov stability and the existence of δ > 0 such that, for every ε > 0,

there exists T = T (ε) > 0 such that kx

k < δ and t

≥ 0 implies that

kx(t)k < ε for all t ≥ t

+ T (ε). That is, for every initial condition in a ball

of radius δ at time t = t

, the graph of the solution of (4.57) is guaranteed

to be inside a given cylinder for all t > t

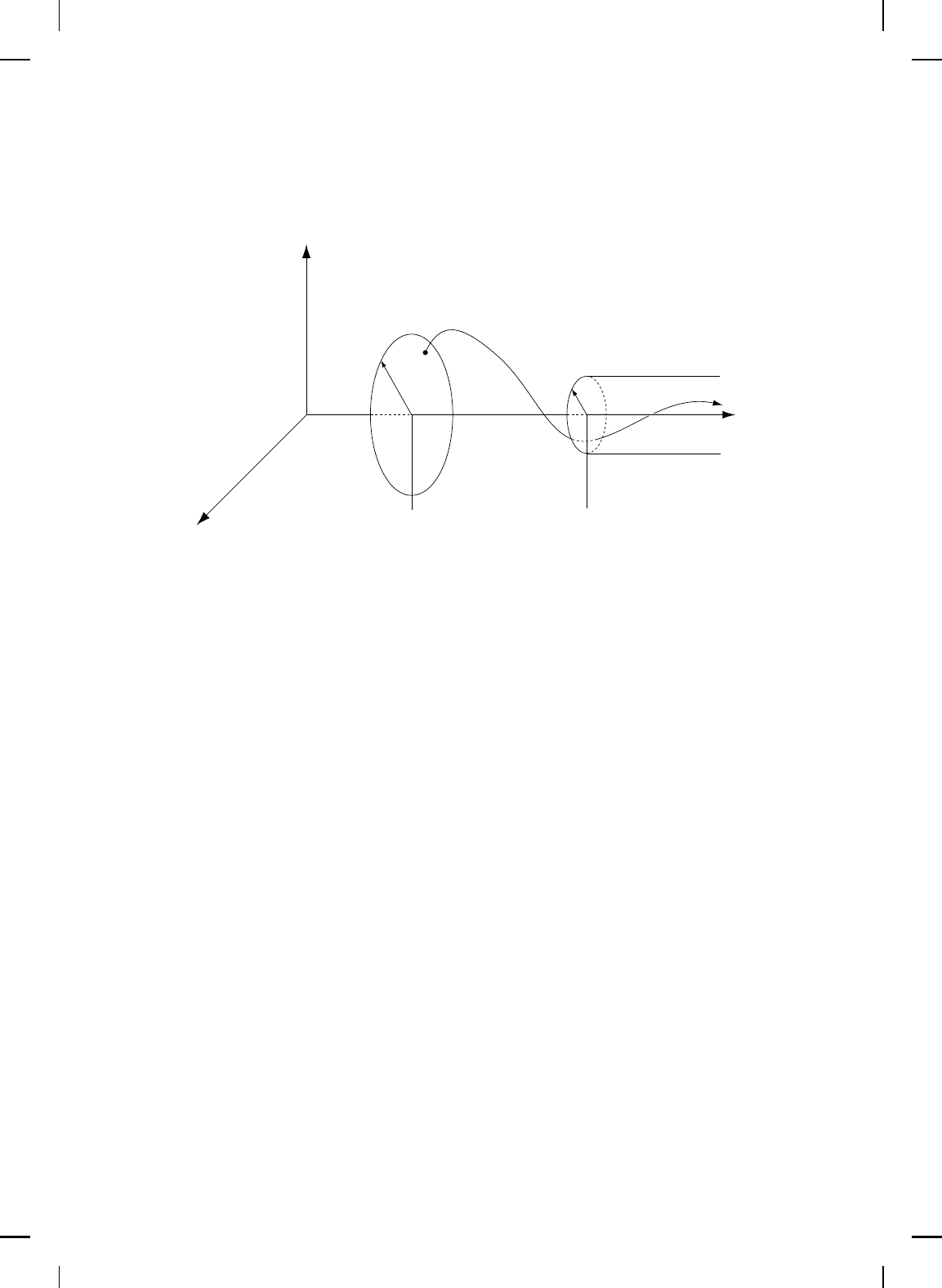
+ T (ε) (see Figure 4.5). Uniform

Lyapunov stability and uniform asymptotic stability can be additionally

NonlinearBook10pt November 20, 2007

ADVANCED STABILITY THEORY 227

characterized by class K and class KL functions. For details, see Problems

4.5 and 4.6.

+ T (ε)

Figure 4.5 Uniform asympt otic stability.

Example 4.4. To elucidate the diﬀerence between Lyapunov stability

and uniform Lyapunov stability consider the scalar linear dynamical system

adopted from [307] given by

˙x(t) = (6t sin t − 2t)x(t), x(t

) = x

, t ≥ t

. (4.58)

The solution of (4.58) is given by

x(t) = x(t

(6s sin s−2s)ds

= x(t

[6 sin t−6t cos t−t

−6 sin t

+6t

cos t

]

. (4.59)

Clearly, for every ﬁxed t

, the term −t

in (4.59) will eventually dominate,

which shows that the exponential term in (4.59) is bounded by a constant

σ(t

) dependent on t

for all t ≥ t

. Hence, |x(t)| < |x(t

)|σ(t

), t ≥ t

Now, given ε > 0, we can choose δ = δ(ε, t

) = ε/σ(t

), which shows that

|x(t

)| < δ implies |x(t)| < ε, t ≥ t

, and hence, the zero solution x(t) ≡ 0

to (4.58) is Lyapunov stable.

Next, suppose t

takes the successive values t

= 2nπ, n = 0, 1, 2, . . .,

and x(t) is evaluated π seconds later for each n. In this case,

x(t

+ π) = x(t

[(4n+1)(6−π)π]

, (4.60)

NonlinearBook10pt November 20, 2007

228 CHAPTER 4

which implies that, for x(t

) 6= 0,

x(t

+ π)

x(t

)

= e

[(4n+1)(6−π)π]

→ ∞ as n → ∞. (4.61)

Since σ(t

) ≥ e

[(4n+1)(6−π)π]

it follows that σ(t

) → ∞ as n → ∞. Thus,

given ε > 0, for stability we need δ = ε/σ(t

) → 0 as t

→ ∞, which shows

that we cannot choose δ independent of t

to satisfy the requirement for

uniform Lyapunov stability. △

Next, using Theorem 4.1 we present suﬃcient conditions for stability

of the n on linear time-varying dynamical system (4.57). For the following

result deﬁne

V (t, x)

△

∂V

∂t

(t, x) +

∂V

∂x

(t, x)f(t, x),

for a given continuously diﬀerentiable fu nction V : [0, ∞) × D → R.

Theorem 4.6. Consider the time-varying dynamical system given by

(4.57). Then the following statements hold:

i) I f there exist a continuously diﬀerentiable function V : [0, ∞)×D → R

and a class K function α(·) such that

V (t, 0) = 0, t ∈ [0, ∞), (4.62)

α(kxk) ≤ V (t, x), (t, x) ∈ [0, ∞) ×D, (4.63)

V (t, x) ≤ 0, (t, x) ∈ [0, ∞) × D, (4.64)

then the nonlinear time-varying dynamical system given by (4.57) is

Lyapunov s table.

ii) If there exist a continuously diﬀerentiable function V : [0, ∞)×D → R

and class K functions α(·), β(·) satisfying (4.63), (4.64), and

V (t, x) ≤ β(kxk), (t, x) ∈ [0, ∞) × D, (4.65)

then the nonlinear time-varying dynamical system given by (4.57) is

uniformly Lyapunov stable.

iii) If there exist continuously diﬀerentiable functions V : [0, ∞) ×D → R

and W : [0, ∞) × D → R, and class K functions α(·), β(·), and γ(·)

such that

W (·, x(·)) is bounded from below or above, (4.62) and (4.63)

hold, and

W (t, 0) = 0, t ∈ [0, ∞), (4.66)

β(kxk) ≤ W (t, x), (t, x) ∈ [0, ∞) × D, (4.67)

V (t, x) ≤ −γ(W (t, x)), (t, x) ∈ [0, ∞) × D, (4.68)

then the zero solution x(t) ≡ 0 to (4.57) is asymptotically stable.

NonlinearBook10pt November 20, 2007

ADVANCED STABILITY THEORY 229

iv) If there exist a continuously diﬀerentiable function V : [0, ∞)×D → R

and class K functions α(·), β(·), γ(·) s atisfying (4.63), (4.65), and

V (t, x) ≤ −γ(kxk), (t, x) ∈ [0, ∞) × D, (4.69)

then the nonlinear time-varying dynamical system given by (4.57) is

uniformly asymptotically stable.

v) If D = R

and there exist continuously diﬀerentiable functions V :

[0, ∞) ×D → R and W : [0, ∞) ×D → R, class K functions β(·), γ(·),

and a class K

∞

function α(·) such that

W (·, x(·)) is bounded from

below or above, and (4.62), (4.63), and (4.66)–(4.68) hold, then the

zero solution x(t) ≡ 0 to (4.57) is globally asymptotically stable.

vi) If D = R

and there exist a continuously diﬀerentiable function V :

[0, ∞) ×R

→ R, a class K function γ(·), class K

∞

functions α(·), β(·)

satisfying (4.63), (4.65), and (4.69), then the nonlinear time-varying

dynamical system given by (4.57) is globally un iformly asymptotically

stable.

vii) If there exist a continuously diﬀerentiable function V : [0, ∞)×D → R

and positive constants α, β, γ, p such th at p ≥ 1 and

αkxk

≤ V (t, x) ≤ βkxk

, (t, x) ∈ [0, ∞) ×D, (4.70)

V (t, x) ≤ −γkxk

, (t, x) ∈ [0, ∞) × D, (4.71)

then the nonlinear time-varying dynamical system given by (4.57) is

(uniformly) exponentially stable.

viii) If D = R

and there exist a continuously diﬀerentiable function V :

[0, ∞) ×R

→ R and positive constants α, β, γ, p ≥ 1 satisfying (4.70)

and (4.71), then the nonlinear time-varying dynamical system given

by (4.57) is globally (uniformly) exponentially stable.

Proof. First note that, requiring the existence of a Lyapunov function

V : [0, ∞) ×D → R satisfyin g the conditions above, it follows from Theorem

2.39 that there exists a unique solution to (4.57) for all t ≥ t

. Next, let

= n, n

= 1, x

(t − t

) = x(t), x

(t − t

) = t, f

, x

) = f(x

, x

), and

, x

) = 1. Now, note that with τ = t−t

, the solution x(t), t ≥ t

, to th e

nonlinear time-varying dynamical system (4.57) is equivalently characterized

by the solution x

(τ), τ ≥ 0, to the nonlinear autonomous dynamical system

˙x

(τ) = f

(τ), x

(τ)), x

(0) = x

, τ ≥ 0,

˙x

(τ) = 1, x

(0) = t

where ˙x

(·) and ˙x

(·) denote diﬀerentiation with respect to τ . Furthermore,

note th at since f (t, 0) = 0, t ≥ 0, it follows that f

(0, x

) = 0, for every

∈ R

. Now, the result is a dir ect consequence of Theorem 4.1.

NonlinearBook10pt November 20, 2007

230 CHAPTER 4

It is important to note that (4.63) along with (4.69) are not suﬃcient

to guarantee asymptotic stability of a nonlinear time-varying dynamical

system. This is shown by the following counterexample adopted from [306].

Example 4.5. Consider th e scalar nonlinear dynamical sys tem given

˙x(t) =

˙g(t)

g(t)

x(t), x(0) = x

, t ≥ 0, (4.72)

where

g(t) =

∞

n=1

1 + n

(t − n)

, t ≥ 0. (4.73)

Note that it can be shown that for every t ≥ 0, g(t) is well deﬁned and

g(t) > 0, t ≥ 0, and hence, the right-hand sid e of (4.72) is well deﬁned.

Furth ermore, note that the solution to (4.72) is given by x(t) =

g(t)

g(0)

Next, note that for all m ∈ Z

g(m) =

∞

n=1

1 + n

(m − n)

> 1.

Now, let t ∈ [0, ∞) and let n

, n

∈ Z

be su ch that n

≤ t ≤ n

. In this

case, for all n ∈ Z

\ {n

, n

1 + n

(t − n)

≤

and

1 + n

(t −n

)

≤ 1, i = 1, 2.

Hence, it follows that

g(t) < 2 +

∞

n=1

, t ≥ 0, (4.74)

which implies that |||g|||

∞

< 10/3.

Next, note that

∞

g(t)dt =

∞

n=1

1 + n

(t − n)

∞

n=1

∞

1 + n

(t − n)

∞

n=1

∞

−n

(1 + t

)

NonlinearBook10pt November 20, 2007

ADVANCED STABILITY THEORY 231

∞

n=1

∞

−∞

(1 + t

)

∞

n=1

< 2π,

which implies that |||g|||

< ∞. Fu rthermore, note that

∞

(t)dt ≤ |||g|||

∞

g(t)dt = |||g|||

∞

|||g|||

20π

Now, consider the Lyapunov function candidate

V (t, x) =

(t)



∞

(s)ds



, (4.75)

and n ote that V (t, 0) = 0, t ≥ 0. Sin ce g(t) ≤ γ, t ≥ 0,

V (t, x) ≥ γ

(t)

≥ x

, t ∈ [0, ∞) x ∈ R,

and since

∞

(t)dt < 20π/3, V (t, x) is a well-deﬁned function. Now, it

is easy to verify that

V (t, x) = −x

. Hence, V (t, x) satisﬁes (4.62), (4.63),

and (4.69), which implies that the zero solution x(t) ≡ 0 is Lyapunov stable.

However, since lim

t→∞

g(t) 6= 0 (since g(m) > 1, m ∈ Z

) it follows that

the zero solution x(t) ≡ 0 to (4.72) is not asymptotically stable. △

In light of Theorem 4.6 it follows that Theorem 4.1 can be trivially

extended to address partial stability for time-varying dynamical systems.

Speciﬁcally, consider the nonlinear time-varying dynamical system

˙x

(t) = f

(t, x

(t), x

(t)), x

) = x

, t ≥ t

, (4.76)

˙x

(t) = f

(t, x

(t), x

(t)), x

) = x

, (4.77)

where x

∈ D, x

∈ R

, f

: [t

, t

) ×D×R

→ R

is such that, for every

t ∈ [t

, t

) and x

∈ R

, f

(t, 0, x

) = 0 and f

(t, ·, x

) is locally Lipschitz in

, and f

: [t

, t

)×D×R

→ R

is such that, for every x

∈ D, f

(·, x

, ·)

is locally Lipschitz in x

. Next, let ˆx

(t−t

) = x

(t), ˆx

(t−t

) = [x

(t) t]

(ˆx

, ˆx

) = f

(t, x

, x

), and

(ˆx

, ˆx

) = [f

(t, x

, x

) 1]

. Now, note that

with τ = t − t

, the solution (x

(t), x

(t)), t ≥ t

, to the nonlinear time-

varying dynamical sy s tem (4.76) and (4.77) is equivalently characterized by

the solution (ˆx

(τ), ˆx

(τ)), τ ≥ 0, to the nonlinear autonomous dynamical

system

ˆx

(τ) =

(ˆx

(τ), ˆx

(τ)), ˆx

(0) = x

, τ ≥ 0, (4.78)

ˆx

(τ) =

(ˆx

(τ), ˆx

(τ)), ˆx

(0) = [x

]

, (4.79)

NonlinearBook10pt November 20, 2007

232 CHAPTER 4

where

ˆx

(·) and

ˆx

(·) denote diﬀerentiation with r espect to τ. Hence,

Theorem 4.1 can be used to derive suﬃcient conditions for partial stability

results for the nonlinear time-varying dynamical systems of the form (4.76)

and (4.77). Of course, in this case it is important to note that partial

stability may be uniform with respect to either or both of x

and t

Using Theorems 4.1 and 4.6 we present some insight on the complexity

of analyzing stability of linear, time-varying systems. Speciﬁcally, let

f(t, x) = A(t)x, where A : [0, ∞) → R

n×n

is continuous, so that (4.57)

becomes

˙x(t) = A(t)x(t), x(t

) = x

, t ≥ t

. (4.80)

Now, in order to analyze the stability of (4.80), let n

= n, n

= 1, x

(t −

) = x(t), x

(t − t

) = t, f

, x

) = A(t)x, and f

, x

) = 1. Hence,

the solution x(t), t ≥ t

, to (4.80) can be equivalently characterized by the

solution x

(τ), τ ≥ 0, to the nonlinear autonomous dynamical system

˙x

(τ) = A(x

(τ))x

(τ), x

(0) = x

, τ ≥ 0, (4.81)

˙x

(τ) = 1, x

(0) = t

, (4.82)

where ˙x

(·) and ˙x

(·) denote diﬀerentiation with respect to τ. It is clear

from (4.81) and (4.82) that in spite of the fact that (4.80) is a linear system,

its solutions are in herently characterized by a nonlinear system of the form

(4.81) and (4.82).

Example 4.6. Consider the linear time-varying dynamical system

˙x

(t) = −x

(t) −e

−t

(t), x

(0) = x

, t ≥ 0, (4.83)

˙x

(t) = x

(t) − x

(t), x

(0) = x

. (4.84)

To examine stability of this system, consider the Lyapunov function

candidate V (t, x) = x

+ (1 + e

−t

. Note that since

+ x

≤ V (t, x) ≤ x

+ 2x

, (x

, x

) ∈ R × R, t ≥ 0, (4.85)

it follows that V (t, x) is positive deﬁnite, radially u nbounded and satisﬁes

(4.63) and (4.65). Next, s ince

V (t, x) = −2x

+ 2x

− 2x

− 3e

−t

≤ −2x

+ 2x

− 2x

= −x

≤ −λ

min

(R)kxk

, (4.86)

where

R =



2 −1

−1 2



> 0

and x = [x

]

, it follows from vi) and vii) of Theorem 4.6 with p = 2

that the zero solution (x

(t), x

(t)) ≡ (0, 0) to (4.83) and (4.84) is globally

NonlinearBook10pt November 20, 2007

ADVANCED STABILITY THEORY 233

exponentially stable. △

Example 4.7. It is important to note that it is not always necessary to

construct a time-varying Lyapunov function to show stability for a nonlinear

time-varying dynamical system. I n particular, consider the nonlinear time-

varying dynamical system

˙x

(t) = −x

(t) + (sin ωt)x

(t), x

(0) = x

, t ≥ 0, (4.87)

˙x

(t) = −(sin ωt)x

(t) −x

(t), x

(0) = x

. (4.88)

To show that the origin is globally uniformly asymptotically stable, consider

the time-invariant Lyapunov function candidate V (x) =

). Clearly,

V (x), x ∈ R

, is positive deﬁnite and r ad ially unbounded. Furthermore,

V (x) = x

[−x

+ (sin ωt)x

] + x

[−(sin ωt)x

− x

]

= −x

− x

< 0, (x

, x

) ∈ R ×R, (x

, x

) 6= (0, 0), (4.89)

which sh ows that the zero solution (x

(t), x

(t)) ≡ (0, 0) to (4.87) and (4.88)

is globally uniformly asymptotically stable. △

Example 4.8. Consider the linear time-varying dy namical system

˙x(t) = A(t)x(t), x(t

) = x

, t ≥ t

, (4.90)

where A : [0, ∞) → R

n×n

is continuous. To examine the stability of

this system, consider the quadratic Lyapunov function candidate V (t, x) =

P (t)x, where P : [0, ∞) → R

n×n

is a continuously diﬀerentiable,

uniformly bounded, and positive-deﬁnite matrix fu nction (that is, P (t) is

positive deﬁnite for every t ≥ t

) satisfying

−

P (t) = A

(t)P (t) + P (t)A(t) + R(t), (4.91)

where R(·) is continuous s uch that R(t) ≥ γI

> 0, γ > 0, for all t ≥

. Now, since P (·) is continuously diﬀerentiable, uniformly bounded, and

positive deﬁnite it follows that there exist α, β > 0 such that

0 < αI

≤ P (t) ≤ βI

, t ≥ t

, (4.92)

and h en ce,

αkxk

≤ V (t, x) ≤ βkxk

. (4.93)

Thus , V (t, x) is positive deﬁnite and radially unb ou nded. Next, since

V (t, x) = x

P (t)x + 2x

P (t)A(t)x

= x

[

P (t) + A

(t)P (t) + P (t)A(t)]x

= −x

R(t)x

≤ −γkxk

, (4.94)

NonlinearBook10pt November 20, 2007

234 CHAPTER 4

it follows from vi) and vii) of Theorem 4.6 with p = 2 that the zero solution

x(t) ≡ 0 to (4.90) is globally exponentially stable. Hence, a suﬃcient

condition f or global exponential stability for a linear time-varying system is

the existence of a continuously d iﬀerentiable, bounded, and positive-deﬁnite

matrix function P : [0, ∞) → R

n×n

satisfying (4.91). △

In C hapter 3 it was shown that for time-invariant dynamical systems

the invariance principle can be used to relax the strict negative-deﬁniteness

condition on the Lyapunov derivative while still ensuring asymptotic

stability of the origin by showing that the set R where the Lyapunov

derivative vanishes contains no invariant set other than the origin. For time-

varying systems, there does not exist an analogous result for establishing

uniform asymptotic stability since, in general, positive limit sets for time-

varying systems are not invariant. However, the following theorem provides

a similar, albeit weaker, result for time-varying systems.

Theorem 4.7 (LaSa lle-Yoshizawa Theorem). Consider the time-

varying dynamical system (4.57) and assume [0, ∞) × D is a positively

invariant set with respect to (4.57) where f (t, ·) is Lipschitz in x, uniformly

in t. Furthermore, assume there exist functions V : [0, ∞) × D → R and

W, W

, W

: D → R such that V (·, ·) is continuously diﬀerentiable, W

(·)

and W

(·) are continuous and positive deﬁnite, W (·) is continuous and

nonnegative deﬁnite, and, for all (t, x) ∈ [0, ∞) × D,

(x) ≤ V (t, x) ≤ W

(x), (4.95)

V (t, x) ≤ −W (x). (4.96)

Then there exists D

⊆ D su ch that for all (t

, x

) ∈ [0, ∞) × D

, x(t) →

△

= {x ∈ D : W (x) = 0} as t → ∞ . If, in addition, D = R

and W

(·) is

radially unbounded, then for all (t

, x

) ∈ [0, ∞) × R

, x(t) → R

△

= {x ∈

: W (x) = 0} as t → ∞.

Proof. The proof is a direct consequence of Theorem 4.2 with n

= n,

= 1, x

(t −t

) = x(t), x

(t − t

) = t, f

, x

) = f(t, x), f

, x

) = 1,

and V (x

, x

) = V (t, x).

If W is a homeomorphism and W

−1

(0) = {0}, then Theorem 4.7

establishes attraction to the origin. Alternatively, if, in place of (4.96),

V (t, x) ≤ 0, (t, x) ∈ [0, ∞) × D, and the integral of

V (t, x) satisﬁes the

inequality

t+ε

V (τ, s(τ, t, x))dτ ≤ − αV (t, x), (4.97)

where α ∈ (0, 1), for all t ≥ 0 and x ∈ D, and some ε > 0, then uniform

asymptotic stability of the zero solution x(t) ≡ 0 to (4.57) can be established.

This result is left as an exercise for the r eader.