Haddad W.M. Nonlinear Dynamical Systems and Control: A Lyapunov-Based Approach
Подождите немного. Документ загружается.


NonlinearBook10pt November 20, 2007
ADVANCED STABILITY THEORY 215
case, W (x
1
(t), x
2
(t)) → 0 as t → ∞, and hence, it f ollows from (4.13) that
x
1
(t) → 0 as t → ∞, proving asymptotic stability of (4.6) and (4.7) with
respect to x
1
.
iv) Lyapunov stability uniformly in x
20
follows from ii). Next, let
ε > 0 and δ = δ(ε) > 0 be such that for every x
10
∈ B
δ
(0), x
1
(t) ∈ B
ε
(0),
t ≥ 0, (the existence of such a (δ, ε) pair follows f rom uniform Lyapunov
stability), and assume that (4.15) holds. Since (4.15) implies (4.10) it f ollows
that for every x
10
∈ B
δ
(0), V (x
1
(t), x
2
(t)) is a nonincreasing function of
time and, since V (·, ·) is bounded from below, it follows from the monotone
convergence theorem (Theorem 2.10) that there exists L ≥ 0 such that
lim
t→∞
V (x
1
(t), x
2
(t)) = L. Now, suppose that for some x
10
∈ B
δ
(0), ad
absurdum, L > 0 so that D
L
△
= {x
1
∈ B
ε
(0) : V (x
1
, x
2
) ≤ L for all x
2
∈ R
n
2
}
is nonempty and x
1
(t) 6∈ D
L
, t ≥ 0. Thus, as in the proof of i), there exists
ˆ
δ > 0 such that B
ˆ
δ
(0) ⊂ D
L
. Hence, it follows from (4.15) that for the given
x
10
∈ B
δ
(0) \D
L
and t ≥ 0,
V (x
1
(t), x
2
(t)) = V (x
10
, x
20
) +
Z
t
0
˙
V (x
1
(s), x
2
(s))ds
≤ V (x
10
, x
20
) −
Z
t
0
γ(kx
1
(s)k)ds
≤ V (x
10
, x
20
) −γ(
ˆ
δ)t.
Letting t >
V (x
10
,x
20
)−L
γ(
ˆ
δ)
, it follows that V (x
1
(t), x
2
(t)) < L, which is a
contradiction. Hence, L = 0, and, since x
10
∈ B
δ
(0) was chosen arbitrarily,
it follows that V (x
1
(t), x
2
(t)) → 0 as t → ∞ for all x
10
∈ B
δ
(0). Now,
since V (x
1
(t), x
2
(t)) ≥ α(kx
1
(t)k) ≥ 0, it follows that α(kx
1
(t)k) → 0
or, equivalently, x
1
(t) → 0 t → ∞, establishing asymp totic stability with
respect to x
1
uniformly in x
20
.
v) Let δ > 0 be such that kx
10
k < δ. Since α(·) is a class K
∞
function,
it follows that there exists ε > 0 s uch that V (x
10
, x
20
) < α(ε). Now, (4.14)
implies that V (x
1
(t), x
2
(t)) is a nonincreasing function of time, and hence,
it follows from (4.9) that α(kx
1
(t)k) ≤ V (x
1
(t), x
2
(t)) ≤ V (x
10
, x
20
) < α(ε),
t ≥ 0. Hence, x
1
(t) ∈ B
ε
(0), t ≥ 0. Now, the proof follows as in the proof of
iii).
vi) Let δ > 0 be such that kx
10
k < δ. Since α(·) is a class K
∞
function,
it follows that there exists ε > 0 such that β(δ) ≤ α(ε). Now, (4.15) implies
that V (x
1
(t), x
2
(t)) is a nonincreasing function of time, and hence, it follows
from (4.11) that α(kx
1
(t)k) ≤ V (x
1
(t), x
2
(t)) ≤ V (x
10
, x
20
) < β(δ) ≤ α(ε),
t ≥ 0. Hence, x
1
(t) ∈ B
ε
(0), t ≥ 0. Now, the proof follows as in the proof of
iv).

NonlinearBook10pt November 20, 2007
216 CHAPTER 4
vii) Let ε > 0 and B
ε
(0) be given as in the proof of i) and let η
△
= αε
p
and δ =
η
β
1/p
. Now, (4.17) implies that
˙
V (x
1
, x
2
) ≤ 0, and hence, as in
the proof of ii), it follows that for all (x
10
, x
20
) ∈ B
δ
(0)×R
n
2
, x
1
(t) ∈ B
ε
(0),
t ≥ 0. Furtherm ore, it follows from (4.16) and (4.17) that for all t ≥ 0 and
(x
10
, x
20
) ∈ B
δ
(0) × R
n
2
,
˙
V (x
1
(t), x
2
(t)) ≤ −γkx
1
(t)k
p
≤ −
γ
β
V (x
1
(t), x
2
(t)),
which implies that
V (x
1
(t), x
2
(t)) ≤ V (x
10
, x
20
)e
−
γ
β
t
.
It now follows from (4.16) that
αkx
1
(t)k
p
≤ V (x
1
(t), x
2
(t)) ≤ V (x
10
, x
20
)e
−
γ
β
t
≤ βkx
10
k
p
e
−
γ
β
t
, t ≥ 0,
and h en ce,
kx
1
(t)k ≤
β
α
1/p
kx
10
ke
−
γ
βp
t
, t ≥ 0,
establishing exponential stability with respect to x
1
uniformly in x
20
.
viii) The proof follows as in vi) and vii).
By setting n
1
= n and n
2
= 0, Theorem 4.1 specializes to the case
of nonlinear autonomous systems of the f orm ˙x
1
(t) = f
1
(x
1
(t)). In this
case, Lyapunov (respectively, asymptotic) stability with respect to x
1
and
Lyapunov (respectively, asymptotic) stability with respect to x
1
uniformly
in x
20
are equivalent to the classical Lyapunov (respectively, asymptotic)
stability of nonlinear autonomous systems presented in Section 3.2. In
particular, note that it follows from Problems 3.75 and 3.76 that there exists
a continuously differentiable fu nction V : D → R such that (4.9), (4.11), and
(4.15) hold if and only if V (0) = 0, V (x
1
) > 0, x
1
6= 0, V
′
(x
1
)f
1
(x
1
) < 0,
x
1
6= 0. In addition, if D = R
n
1
and there exist class K
∞
functions α(·), β(·)
and a continuously differentiable function V (·) such that (4.9), (4.11), and
(4.15) hold if and only if V (0) = 0, V (x
1
) > 0, x
1
6= 0, V
′
(x
1
)f
1
(x
1
) < 0,
x
1
6= 0, and V (x
1
) → ∞ as kx
1
k → ∞. Hence, in this case, Theorem
4.1 collapses to the classical Lyapunov stability theorem for autonomous
systems given in Section 3.2.
It is important to note th at there is a key difference between the
partial stability definitions given in Definition 4.1 and the definitions of
partial stability given in [374, 448]. In particular, the partial stability
definitions given in [374, 448] require that both the initial conditions x
10
and x
20
lie in a neighborhood of the origin, whereas in Definition 4.1 x
20
can be arbitrary. As will be seen in the next section, this difference allows

NonlinearBook10pt November 20, 2007
ADVANCED STABILITY THEORY 217
us to unify autonomous partial stability theory with time-varying stability
theory. Lyapunov (respectively, asymptotic) stability with respect to x
1
given in Definition 4.1 is referred to in [448] as x
1
-stability (respectively, x
1
-
asymptotic stability) for large x
2
while Lyapunov (respectively, asymptotic)
stability with respect to x
1
uniformly in x
20
given in Definition 4.1 is referred
to in [448] as x
1
-stability (respectively, x
1
-asymptotic stability) with respect
to the whole of x
2
. Note that if a nonlinear dynamical system is Lyapunov
(respectively, asymptotically) stable with respect to x
1
in the sense of
Definition 4.1, then the system is x
1
-stable (respectively, x
1
-asymptotically
stable) in the sense of the definition given in [374, 448]. Furthermore, if
there exist a continuously differentiable function V : D × R
n
2
→ R and a
class K function α(·) (respectively, class K functions β(·) and γ(·)) such
that V (0, 0) = 0 and (4.9) and (4.10) (respectively, (4.9), (4.11), and
(4.15)) hold, then the nonlinear dynamical system (4.6) and (4.7) is x
1
-
stable (respectively, uniformly asymptotically x
1
-stable with respect to x
20
)
in the sense of the definition given in [448]. It is important to note that
the condition V (0, x
2
) = 0, x
2
∈ R
n
2
, allows us to prove partial stability
in the sense of Definition 4.1. Finally, an additional difference between our
formulation of the partial stability problem and the partial stability problem
considered in [374, 448] is in the treatment of the equilibrium of (4.6) and
(4.7). Specifically, in our formulation, we require the partial equilibrium
condition f
1
(0, x
2
) = 0 for every x
2
∈ R
n
2
, whereas in [374,448], th e authors
require the equilibrium cond ition f
1
(0, 0) = 0 and f
2
(0, 0) = 0.
Example 4.1. In this example, we use Theorem 4.1 to show that
the rotational/translational proof-mass model (4.4) and (4.5) is partially
Lyapunov stable with respect to q, ˙q, and
˙
θ. To show this, let x
1
= q,
x
2
= ˙q, x
3
= θ, x
4
=
˙
θ and consider the Lyapunov function candidate
V (x
1
, x
2
, x
3
, x
4
) =
1
2
[kx
2
1
+ (M + m)x
2
2
+ (I + me
2
)x
2
4
+ 2mex
2
x
4
cos x
3
].
(4.20)
Note that V (x
1
, x
2
, x
3
, x
4
) =
1
2
kx
2
1
+
1
2
˜x
T
P (x
3
)˜x, where ˜x = [x
2
x
4
]
T
and
P (x
3
) =
M + m me cos x
3
me cos x
3
I + me
2
. (4.21)
Since
2λ
min
(P (x
3
)) = M + m + I + me
2
−
p
(M + m − I − me
2
)
2
+ 4m
2
e
2
cos
2
x
3
, (4.22)
2λ
max
(P (x
3
)) = M + m + I + me
2
+
p
(M + m − I − me
2
)
2
+ 4m
2
e
2
cos
2
x
3
, (4.23)
it follows that α
min
I
2
≤ 2P (x
3
) ≤ α
max
I
2
, x
3
∈ R, where
α
min
△
= M + m + I + me
2
−
p
(M + m − I − me
2
)
2
+ 4m
2
e
2
, (4.24)
NonlinearBook10pt November 20, 2007
218 CHAPTER 4
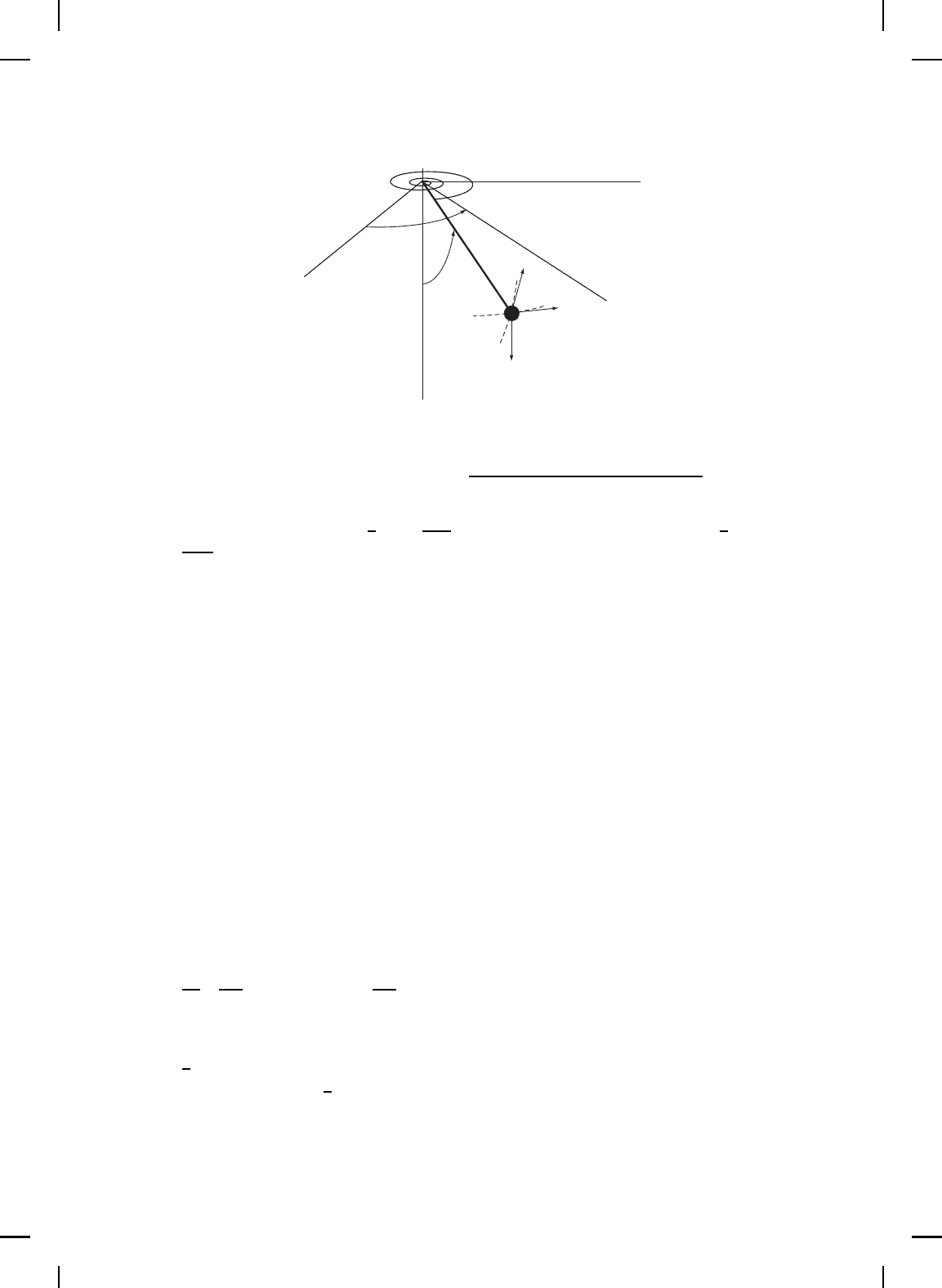
θ
φ
L
k
L
˙
θ
mg
L
˙
φ sin θ
z
y
x
Figure 4.4 Spherical pendulum.
α
max
△
= M + m + I + me
2
+
p
(M + m − I − me
2
)
2
+ 4m
2
e
2
. (4.25)
Hence, it f ollows that
1
2
x
2
1
+
α
min
4
(x
2
2
+ x
2
4
) ≤ V (x
1
, x
2
, x
3
, x
4
) ≤
1
2
x
2
1
+
α
max
4
(x
2
2
+ x
2
4
), which implies that V (·) satisfies (4.9) and (4.11). Now,
since
˙
V (x
1
, x
2
, x
3
, x
4
) = 0, it follows from ii) of Theorem 4.1 that (4.4) and
(4.5) is Lyapunov stable with respect to x
1
, x
2
, and x
4
uniformly in x
30
.
Furth ermore, since the system involves a nonlinear coupling of an u ndamped
oscillator with a rotational rigid body m ode it follows that x
3
(t) does not
converge as t → ∞. △
Example 4.2. In this example, we apply Theorem 4.1 to a Lagrange-
Dirichlet problem involving a conservative Euler-Lagrange system with
a nonnegative-definite kinetic energy function T and a positive-definite
potential function U. Specifically, we consider the motion of the spherical
pendulum shown in Figure 4.4, where θ denotes the angular position of the
pendulum with respect to vertical z-axis, φ denotes the angular position of
the pendulum in the x-y plane, m d en otes the mass of the pendulum, L
denotes the length of the pendulum, k d en otes the torsional spring stiffness,
and g denotes the gravitational acceleration. Defining q
△
= [θ φ]
T
to be the
generalized system positions and ˙q
△
= [
˙
θ
˙
φ]
T
to be the generalized system
velocities, it follows that the governing equations of motion are given by the
Euler-Lagrange equation
d
dt
∂L
∂ ˙q
(q(t), ˙q(t))
−
∂L
∂q
(q(t), ˙q(t))
= 0, q(0) = q
0
, ˙q(0) = ˙q
0
, t ≥ 0,
(4.26)
where L(q, ˙q) = T (q, ˙q) − U (q) denotes the system Lagrangian, T (q, ˙q)
△
=
1
2
m[(L
˙
θ)
2
+ (
˙
φL sin θ)
2
] d en otes the system kinetic energy, and U(q)
△
=
mgL(1 − cos θ) +
1
2
kφ
2
denotes the system potential energy. Equivalently,

NonlinearBook10pt November 20, 2007
ADVANCED STABILITY THEORY 219
(4.26) can be rewritten as
¨
θ(t) − sin θ(t) cos θ(t)
˙
φ
2
(t) + (g/L) sin θ(t) = 0,
θ(0) = θ
0
,
˙
θ(0) =
˙
θ
0
, t ≥ 0, (4.27)
sin
2
θ(t)
¨
φ(t) + 2 sin θ(t) cos θ(t)
˙
φ(t)
˙
θ(t) + (k/mL
2
)φ(t) = 0,
φ(0) = φ
0
,
˙
φ(0) =
˙
φ
0
. (4.28)
Next, consider the Lagrange-Dirichlet energy function V (q, ˙q) = T (q,
˙q) + U(q) and note that since the system kinetic energy function T (q, ˙q)
is not positive definite in ˙q at θ such that sin θ = 0, the function V (q, ˙q)
cannot be used as a Lyapunov function candidate to analyze the stability
of the system using standard Lyapunov th eory. However, the Lagrange-
Dirichlet energy function V (q, ˙q) can be used as a valid Lyapun ov function
within p artial stability theory to gu arantee partial Lyapunov stability with
respect to [θ φ
˙
θ]
T
. Specifically, let x
1
= [θ φ
˙
θ]
T
, let x
2
=
˙
φ, and let
α(s) = max{mgL(1 − cos(s),
1
2
ks
2
,
1
2
mL
2
s
2
} and kx
1
k = max{|θ|, |φ|, |
˙
θ|}.
Now, note that α(·) is a class K function and V (x
1
, x
2
) = V (q, ˙q) ≥ α(kx
1
k).
Furth ermore, note that V (0, x
2
) = 0, x
2
∈ R, and
˙
V (x
1
, x
2
) = 0. Now, it
follows from i) of Th eorem 4.1 that the Euler-Lagrange system given by
(4.27) and (4.28) is partially Lyapunov stable with respect to x
1
. Finally, it
can be easily shown via simulations that the E uler-Lagrange system given
by (4.27) and (4.28) is not Lyapunov stable in the standard s ense. △
Another important app lication of partial stability th eory is the
unification it pr ovides between time-invariant stability theory and stability
theory for time-varying systems. To see this, consider the time-varying
nonlinear dynamical system given by
˙x(t) = f (t, x(t)), x(t
0
) = x
0
, t ≥ t
0
, (4.29)
where x(t) ∈ R
n
, t ≥ t
0
, and f : [t
0
, t
1
)×R
n
→ R
n
. Now, define x
1
(τ)
△
= x(t)
and x
2
(τ)
△
= t, where τ
△
= t − t
0
, and note that the solution x(t), t ≥ t
0
,
to the non linear time-varying dynamical system (4.29) can be equivalently
characterized by the solution x
1
(τ), τ ≥ 0, to the nonlinear autonomous
dynamical system
˙x
1
(τ) = f(x
2
(τ), x
1
(τ)), x
1
(0) = x
0
, τ ≥ 0, (4.30)
˙x
2
(τ) = 1, x
2
(0) = t
0
, (4.31)
where ˙x
1
(·) and ˙x
2
(·) denote differentiation with respect to τ. However,
in this case, stability results for time-invariant systems do not apply to
the augmented system (4.30) and (4.31) since one of the states, namely, the
state x
2
representing time, is unb ou nded. However, w riting the time-varying
nonlinear system (4.29) as (4.30) and (4.31), it is clear that partial stability
theory provides a natural formulation for addressing stability theory for

NonlinearBook10pt November 20, 2007
220 CHAPTER 4
autonomous and nonautonomous systems within a unified framework. The
following example demonstrates the utility of Theorem 4.1 to the stability
of time-varying systems.
Example 4.3. Consider the spring-mass-damper s ystem with time-
varying damping coefficient given by
¨q(t) + c(t) ˙q(t) + kq(t) = 0, q(0) = q
0
, ˙q(0) = ˙q
0
, t ≥ 0. (4.32)
This is an interesting system to analyze since physical intuition would lead
one to surmise that if c(t) ≥ α > 0, t ≥ 0, then the zero solution (q(t), ˙q(t)) ≡
(0, 0) to (4.32) is asymptotically stable since we have constant dissipation of
energy. However, this is not the case. A simple counterexample (see [424]) is
c(t) = 2+e
t
, k = 1, with q(0) = 2 and ˙q(0) = −1, which gives q(t) = 1+e
−t
,
t ≥ 0, and hen ce, q(t) → 1 as t → ∞. This is due to the fact that dampin g
increases so fast that the system halts at q = 1.
To analyze (4.32) using Theorem 4.1, we consider c(t) = 3 + sin t and
k > 1. Now, (4.32) can be equivalently written as
˙z
1
(t) = z
2
(t), z
1
(0) = q
0
, t ≥ 0, (4.33)
˙z
2
(t) = −kz
1
(t) −c(t)z
2
(t), z
2
(0) = ˙q
0
, (4.34)
where z
1
△
= q and z
2
△
= ˙q. Next, let n
1
= 2, n
2
= 1, x
1
= [z
1
, z
2
]
T
,
x
2
= t, f
1
(x
1
, x
2
) = [x
T
1
v, −x
T
1
h(x
2
)]
T
, and f
2
(x
1
, x
2
) = 1, where h(x
2
) =
[k, c(x
2
)]
T
and v = [0, 1]
T
. Now, the solution (z
1
(t), z
2
(t)), t ≥ 0, to the
nonlinear time-varying dynamical s ystem (4.33) and (4.34) is equivalently
characterized by the solution x
1
(t), t ≥ 0, to the nonlinear autonomous
dynamical system
˙x
1
(t) = f
1
(x
1
(t), x
2
(t)), x
1
(0) = [q
0
, ˙q
0
]
T
, t ≥ 0, (4.35)
˙x
2
(t) = 1, x
2
(0) = 0. (4.36)
To examine the stability of this system, consider the Lyapunov
function candidate V (x
1
, x
2
) = x
T
1
P (x
2
)x
1
, where
P (x
2
) =
k + 3 + sin(x
2
) 1
1 1
.
Note that since
x
T
1
P
1
x
1
≤ V (x
1
, x
2
) ≤ x
T
1
P
2
x
1
, (x
1
, x
2
) ∈ R
2
× R, (4.37)
where
P
1
=
k + 2 1
1 1
, P
2
=
k + 4 1
1 1
,

NonlinearBook10pt November 20, 2007
ADVANCED STABILITY THEORY 221
it f ollows that V (x
1
, x
2
) satisfies (4.16) with D = R
2
and p = 2. Next, since
˙
V (x
1
, x
2
) = −2x
T
1
[R + R
1
(x
2
)]x
1
≤ −2x
T
1
Rx
1
≤ −min{k − 1, 1}kx
1
k
2
2
, (4.38)
where R = diag[k − 1, 1] > 0 and R
1
(x
2
) = diag[1 −
1
2
cos(x
2
), 1 + sin(x
2
)],
it follows from v) and vi) of Theorem 4.1 that the dynamical system (4.35)
and (4.36) is globally exponentially stable with respect to x
1
uniformly in
x
20
. △
In the case of time-invariant systems the Barbashin-Krasovskii-LaSalle
invariance theorem (Theorem 3.3) shows that bounded system tr aj ectories
of a nonlinear dynamical system approach the largest invariant set M
characterized by the set of all points in a compact set D of the state
space where the Lyapunov derivative identically vanishes. In the case of
partially stable systems, however, it is not generally clear how to define
the set M since
˙
V (x
1
, x
2
) is a function of both x
1
and x
2
. However, if
˙
V (x
1
, x
2
) ≤ −W (x
1
) ≤ 0, where W : D → R is continuous and nonnegative
definite, then a set R ⊃ M can be defined as the set of points where W (x
1
)
identically vanishes, that is, R = {x
1
∈ D : W (x
1
) = 0}. In this case, as
shown in the next theorem, the partial system trajectories x
1
(t) approach
R as t tends to infinity. For this r esult, the following lemma, known as
Barbalat’s lemma, is necessary.
Lemma 4.1 (Barbalat’s Lemma ) . Let σ : [0, ∞) → R be a uniformly
continuous function and s uppose that lim
t→∞
R
t
0
σ(s)ds exists and is finite.
Then, lim
t→∞
σ(t) = 0.
Proof. Suppose, ad absurdum, that lim sup
t→∞
|σ(t)| > 0 and let α
1
∈
R be such th at 0 < α
1
< lim sup
t→∞
|σ(t)|. In this case, for every T
1
> 0,
there exists t
′
1
≥ T
1
such that |σ(t
′
1
)| ≥ α
1
. Next, since σ : [0, ∞) → R is
uniformly continuous, it follows that there exists α
2
= α
2
(α
1
) > 0 such that
|σ(t + τ ) − σ(t)| < α
1
/2 for all t ≥ 0 and τ ∈ [0, α
2
]. Hence,
|σ(t)| = |σ(t) − σ(t
′
1
) + σ(t
′
1
)|
≥ |σ(t
′
1
)| −|σ(t) − σ(t
′
1
)|
> α
1
/2, t ∈ [t
′
1
, t
′
1
+ α
2
]. (4.39)
Now, since σ : [0, ∞) → R is continuous and |σ(t)| > α
1
/2 > 0, t ∈ [t
′
1
, t
′
1
+
α
2
], it follows that the sign of σ(t) is constant over t ∈ [t
′
1
, t
′
1
+ α
2
]. Hence,
Z
t
′
1
+α
2
t
′
1
σ(t)dt
=
Z
t
′
1
+α
2
t
′
1
|σ(t)|dt >
1
2
α
1
α
2
. (4.40)
Now, repeating the above argument it can be shown that there exists a

NonlinearBook10pt November 20, 2007
222 CHAPTER 4
sequence {t
′
i
}
∞
i=1
such that t
′
i
+ α
2
≤ t
′
i+1
, i = 1, 2, . . ., and
R
t
′
i
+α
2
t
′
i
|σ(t)dt >
1
2
α
1
α
2
, i = 1, 2, . . .. Hence,
Z
∞
0
|σ(t)|dt ≥
∞
X
i=1
Z
t
′
i
+α
2
t
′
i
|σ(t)|dt > α
1
∞
X
i=1
α
2
= ∞, (4.41)
which is a contradiction.
Theorem 4.2. Consider the nonlinear dynamical system (4.6) and
(4.7), and assume D × R
n
2
is a positively invariant set with respect to
(4.6) and (4.7) where f
1
(·, x
2
) is Lipschitz continuous in x
1
, uniformly
in x
2
. Furthermore, assume there exist functions V : D × R
n
2
→ R,
W, W
1
, W
2
: D → R such that V (·, ·) is continuously differentiable, W
1
(·)
and W
2
(·) are continuous and positive definite, W (·) is continuous and
nonnegative definite, and, for all (x
1
, x
2
) ∈ D × R
n
2
,
W
1
(x
1
) ≤ V (x
1
, x
2
) ≤ W
2
(x
1
), (4.42)
˙
V (x
1
, x
2
) ≤ −W (x
1
). (4.43)
Then there exists D
0
⊆ D such that for all (x
10
, x
20
) ∈ D
0
× R
n
2
, x
1
(t) →
R
△
= {x
1
∈ D : W (x
1
) = 0} as t → ∞. If, in addition, D = R
n
1
and W
1
(·) is
radially unbounded, then for all (x
10
, x
20
) ∈ R
n
1
× R
n
2
, x
1
(t) → R
△
= {x
1
∈
R
n
1
: W (x
1
) = 0} as t → ∞.
Proof. Assume (4.42) and (4.43) hold. Then it follows from Theorem
4.1 that the nonlinear dynamical system given by (4.6) and (4.7) is Lyapunov
stable with respect to x
1
uniformly in x
20
. Let ε > 0 be such that B
ε
(0) ⊂ D
and let δ = δ(ε) > 0 be such that if x
10
∈ B
δ
(0), then x
1
(t) ∈ B
ε
(0),
t ≥ 0. Now, since V (x
1
(t), x
2
(t)) is nonincreasing and bounded from below
by zero, it follows from the monotone convergence theorem (Theorem 2.10)
that lim
t→∞
V (x
1
(t), x
2
(t)) exists and is finite. Hence, since for every t ≥ 0,
Z
t
0
W (x
1
(τ))dτ ≤ −
Z
t
0
˙
V (x
1
(τ), x
2
(τ))dτ = V (x
10
, x
20
) − V (x
1
(t), x
2
(t)),
it follows that lim
t→∞
R
t
0
W (x
1
(τ))dτ exists and is finite.
Next, since by (4.42) kx
1
(t)k ≤ ε, t ≥ 0, and, for every x
2
∈ R
n
2
,
f
1
(·, x
2
) is Lipschitz continuous on D uniformly in x
2
, it follows that
kx
1
(t
2
) −x
1
(t
1
)k =
Z
t
2
t
1
f
1
(x
1
(τ), x
2
(τ))dτ
≤ L
1
Z
t
2
t
1
kx
1
(τ)kdτ
≤ L
1
ε(t
2
− t
1
), t
2
≥ t
1
, (4.44)
NonlinearBook10pt November 20, 2007
ADVANCED STABILITY THEORY 223
where L
1
is th e Lipschitz constant of f
1
(·, ·) on {x
1
∈ D : kx
1
k ≤ ε}. Now,
for every ˆε > 0, letting δ = δ(ˆε) =
ˆε
L
1
ε
yields
kx
1
(t
2
) −x
1
(t
1
)k < ˆε, t
2
− t
1
≤ δ,
which shows that x
1
(·) is uniformly continuous. Next, since x
1
(·) is
uniformly continuous and W (·) is continuous on a compact set B
ε
(0), it
follows that W (x
1
(t)) is uniform ly continuous at every t ≥ 0. Now, it
follows f rom Barbalat’s lemma (Lemma 4.1) that W (x
1
(t)) → 0 as t → ∞.
Finally, if, in addition, D = R
n
1
and W
1
(·) is radially unbounded, then, as
in the proof of iv) of Theorem 4.1, f or every x
10
∈ R
n
1
there exists ε, δ > 0
such that x
10
∈ B
δ
(0) and x
1
(t) ∈ B
ε
(0), t ≥ 0. Now, the proof follows by
repeating th e above arguments.
Theorem 4.2 shows that the partial system traj ectories x
1
(t) app roach
R as t tends to infinity. However, since the positive limit s et of the partial
trajectory x
1
(t) is a subset of R, Theorem 4.2 is a weaker result than the
standard invariance principle wherein one would conclude that the partial
trajectory x
1
(t) approaches the largest invariant set M contained in R. This
is not tru e in general for partially stable systems since the positive limit set of
a partial traj ectory x
1
(t), t ≥ 0, is not an invariant set. However, in the case
where f
1
(·, x
2
) is periodic, almost periodic, or asymptotically independent of
x
2
, then an invariance principle for partially stable systems can be derived.
This result is left as an exercise for the reader.
Next, we state two converse theorems for partial stability. The proofs
of these theorems are virtually identical to the proofs of the converse
theorems given in Section 3.5 and are left as exercises for the reader.
Theorem 4.3. Assume that the n onlinear dyn amical system (4.6) and
(4.7) is asymptotically stable with respect to x
1
uniformly in x
20
and f
1
:
D×R
n
2
→ R
n
1
and f
2
: D×R
n
2
→ R
n
2
are continuously differentiable. Let
δ > 0 be such th at B
δ
(0) ⊂ D and x
10
∈ B
δ
(0) implies that lim
t→∞
x
1
(t) = 0
uniformly in x
10
and x
20
for all x
20
∈ R
n
2
, and assume
∂f
∂x
1
is bounded on
B
δ
(0) u niformly in x
2
. Then there exist a continuously differentiable function
V : B
δ
(0) × R
n
2
→ R and class K functions α(·), β(·), and γ(·) such that
α(kx
1
k) ≤ V (x
1
, x
2
) ≤ β(kx
1
k), (x
1
, x
2
) ∈ B
δ
(0) × R
n
2
, (4.45)
˙
V (x
1
, x
2
) ≤ −γ(kx
1
k), (x
1
, x
2
) ∈ B
δ
(0) × R
n
2
. (4.46)
Theorem 4.4. Assume that the n onlinear dyn amical system (4.6) and
(4.7) is exponentially stable with respect to x
1
uniformly in x
20
and f
1
: D×
R
n
2
→ R
n
1
and f
2
: D×R
n
2
→ R
n
2
are continuously differentiable. Let δ > 0
be s uch that B
δ
(0) ⊂ D and x
10
∈ B
δ
(0) implies that kx
1
(t)k ≤ αkx
10
ke
−βt
for some α, β > 0 and for all t ≥ 0 and x
20
∈ R
n
2
, and assume
∂f
∂x
1
is bounded

NonlinearBook10pt November 20, 2007
224 CHAPTER 4
on B
δ
(0) uniformly in x
2
. Then, for every p > 1, there exist a continuously
differentiable function V : B
δ
(0)×R
n
2
→ R and positive constants α, β, and
γ su ch that
αkx
1
k
p
≤ V (x
1
, x
2
) ≤ βkx
1
k
p
, (x
1
, x
2
) ∈ B
δ
(0) ×R
n
2
, (4.47)
˙
V (x
1
, x
2
) ≤ −γkx
1
k
p
, (x
1
, x
2
) ∈ B
δ
(0) × R
n
2
. (4.48)
Finally, we close this section by addressing a partial stability notion
wherein both initial conditions x
10
and x
20
lie in a neighborhood of the
origin. For this result we modify Definition 4.1 to reflect the fact that the
entire initial state x
0
= [x
T
10
, x
T
20
]
T
lies in the neighborhood of the origin so
that kx
10
k < δ is replaced by kx
0
k < δ in the definition. Furthermore, for
this result we assume f
1
: D × R
n
2
→ R
n
1
and f
2
: D × R
n
2
→ R
n
2
are such
that f
1
(0, 0) = 0 and f
2
(0, 0) = 0.
Theorem 4.5. Consider the nonlinear dynamical system (4.6) and
(4.7). Then the following statements hold:
i) I f there exist a continuous ly differentiable function V : D × R
n
2
→ R
and a class K function α(·) such that V (0, 0) = 0,
α(kx
1
k) ≤ V (x
1
, x
2
), (x
1
, x
2
) ∈ D × R
n
2
, (4.49)
˙
V (x
1
, x
2
) ≤ 0, (x
1
, x
2
) ∈ D × R
n
2
, (4.50)
then the nonlinear dynamical system given by (4.6) and (4.7) is
Lyapunov s table with respect to x
1
.
ii) If there exist a continuously differentiable fun ction V : D × R
n
2
→ R
and class K functions α(·), β(·) satisfying (4.49), (4.50), and
V (x
1
, x
2
) ≤ β(kxk), (x
1
, x
2
) ∈ D × R
n
2
, (4.51)
where x
△
= [x
T
1
, x
T
2
]
T
, then the n onlinear dynamical system given by
(4.6) and (4.7) is Lyapunov stable with respect to x
1
uniformly in x
20
.
iii) If there exist continuously differentiable functions V : D × R
n
2
→ R
and W : D ×R
n
2
→ R, and class K functions α(·), β(·), and γ(·) such
that
˙
W (x
1
(·), x
2
(·)) is bounded from below or above, (4.49) holds, and
β(kxk) ≤ W (x
1
, x
2
), (x
1
, x
2
) ∈ D × R
n
2
, (4.52)
˙
V (x
1
, x
2
) ≤ −γ(W (x
1
, x
2
)), (x
1
, x
2
) ∈ D × R
n
2
, (4.53)
then the nonlinear dynamical system given by (4.6) and (4.7) is
asymptotically stable with respect to x
1
.
iv) If there exist a continuously differentiable function V : D × R
n
2
→ R
and class K functions α(·), β(·), γ(·) s atisfying (4.49), (4.51), and
˙
V (x
1
, x
2
) ≤ −γ(kxk), (x
1
, x
2
) ∈ D × R
n
2
, (4.54)
