Haddad W.M. Nonlinear Dynamical Systems and Control: A Lyapunov-Based Approach

Подождите немного. Документ загружается.

NonlinearBook10pt November 20, 2007

STABILITY THEORY FOR NONLINEAR SYSTEMS 205

Finally, the concept of s emistability introduced in Problem 3.44 is due

to Bhat and Bernstein [54] for nonlinear systems and Campbell and Rose [81]

for linear systems. See also Bernstein and Bhat [46]. Finite-time stability

as introduced in Problem 3.43 is due to Bhat and Bernstein [55]. Stability

theory for functional retarded systems as introduced in Problem 3.65 is due

to Krasovskii [245] with an excellent textbook treatment given by Hale and

Lunel [181].

NonlinearBook10pt November 20, 2007

Chapter Four

Advanced Stability Theory

4.1 Introduction

In Chapter 3, we developed the basic concepts and mathematical tools for

Lyapunov stability theory. In this chapter, we present several generalizations

and extensions of Lyapunov stability theory. In particular, partial stability

theorems are presented and derived, wherein stability with respect to

part of the system state is addressed. In addition, we present stability

theorems for time-varying nonlinear dynamical systems as a special case of

partial stability. Lagrange stability, boundedness, ultimate boun dedness,

input-to-state stability, ﬁnite-time stability, and semistability notions are

also p resented. Finally, advanced stability theorems involving generalized

Lyapunov functions, stability of sets, stability of periodic orbits, and

stability theorems via vector L yapunov fu nctions are also established.

4.2 Partial Stability o f Nonlinear Dynamical Systems

In m any engineering applications, partial stability, that is, stability with

respect to part of the system’s states, is often necessary. I n particular,

partial stability arises in the study of electromagnetics [482], inertial

navigation systems [403], spacecraft stabilization via gimballed gyroscopes

and/or ﬂywheels [448], combustion s y s tems [16], vibrations in rotating

machinery [289], and biocenology [368], to cite but a few examples. For

example, in the ﬁeld of biocenology involving Lotka-Volterra predator-prey

models of population dynamics with age structure, if some of the species

preyed upon are left alone, then the corresponding population increases

without b ound while a subset of the prey species remains stable [368,

pp. 260–269]. The need to consider partial stability in the aforementioned

systems arises from the fact that stability notions involve equilibrium

co ordinates as well as a hyperplane of coordinates that is closed but not

compact. Hence, partial stability involves motion lying in a subspace instead

of an equilibrium point.

NonlinearBook10pt November 20, 2007

208 CHAPTER 4

Motor

Figure 4.1 Slider-crank mechanism.

Additionally, partial stabilization, that is, closed-loop stability with

respect to part of the closed-lo op system’s state, also arises in many

engineering applications [289, 448]. S peciﬁcally, in spacecraft stabilization

via gimballed gyroscop es asymp totic stability of an equilibrium position

of the spacecraft is sought wh ile requiring Lyapunov stability of the axis

of the gyroscope relative to the spacecraft [448]. Alternatively, in th e

control of rotating machinery with mass imbalance, spin stabilization about

a nonprincipal axis of inertia requires motion stabilization with respect

to a s ubspace instead of the origin [289]. Perhaps the most common

application wh ere partial stabilization is necessary is adaptive control,

wherein asymptotic stability of the closed-loop p lant states is guaranteed

without necessarily achieving parameter error convergence.

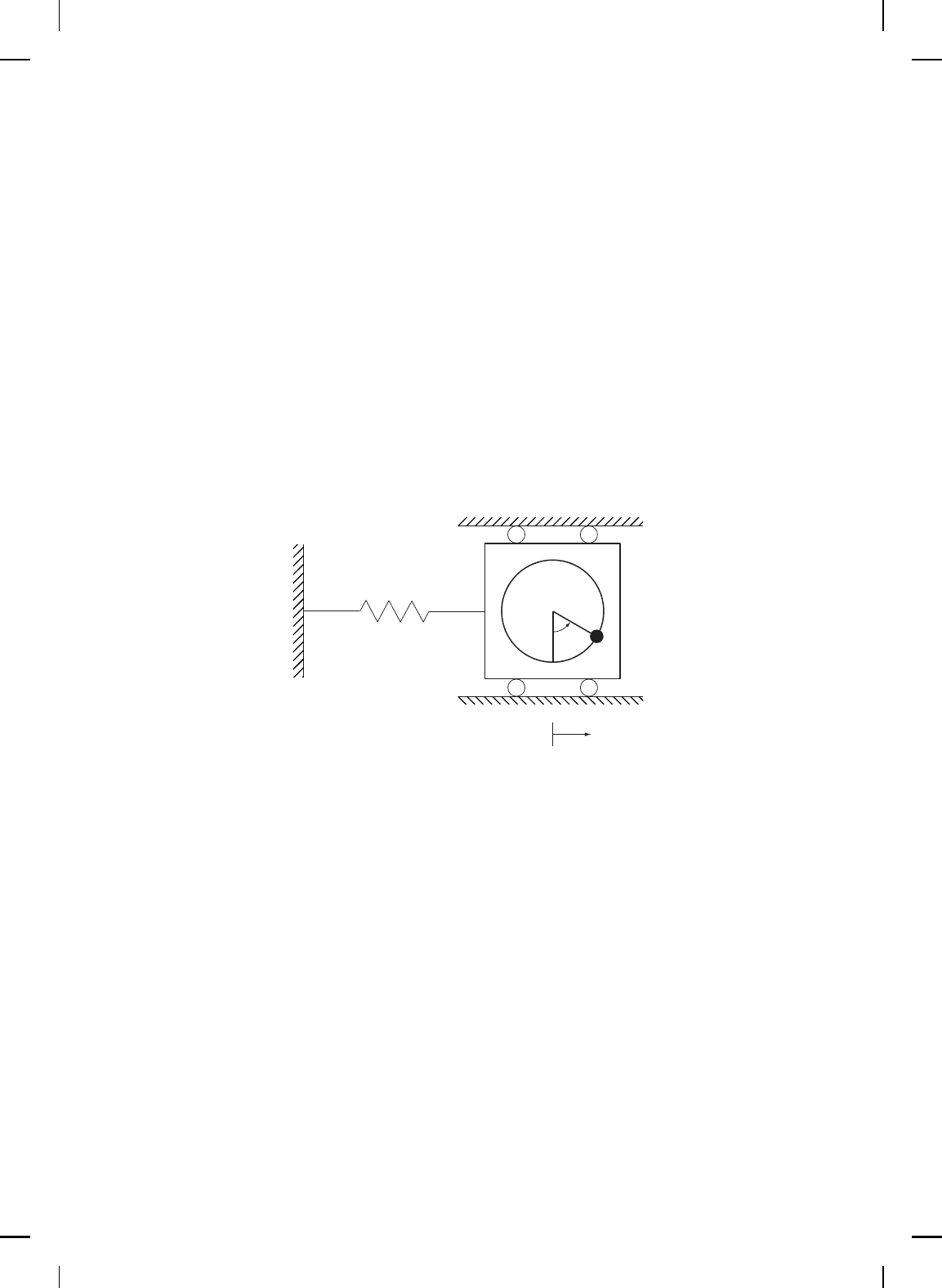
To further demonstrate the utility and need for partial stability theory,

we consider two simple examples. Speciﬁcally, consider the equation of

motion for the slider-crank mechanism shown in Figure 4.1 given by [44,199]

m(θ(t))

θ(t) + c(θ(t))

(t) = u(t), θ(0) = θ

θ(0) =

, t ≥ 0, (4.1)

where

m(θ) = m

+ m

sin θ +

r cos θ sin θ

− r

sin

, (4.2)

c(θ) = m

sin θ +

r cos θ sin θ

− r

sin



cos θ + r

(1 − 2 sin

θ) + r

sin

− r

sin

θ)

3/2



, (4.3)

and m

are point masses, r and l are the lengths of the rods, and

u(·) is the control torque applied by the motor. Now, suppose we choose

the feedback control law u = φ(θ,

θ) s o that the an gular velocity of the

crank is constant, that is,

θ(t) → Ω as t → ∞, where Ω > 0. This implies

that θ(t) ≈ Ωt → ∞ as t → ∞. Furthermore, since m(θ) and c(θ) are

functions of θ we cannot ignore the angular position θ. Hence, sin ce θ does

not converge, it is clear that (4.1) is unstable in the standard sense but

NonlinearBook10pt November 20, 2007

ADVANCED STABILITY THEORY 209

partially asymptotically stable with respect to

θ (see Deﬁnition 4.1).

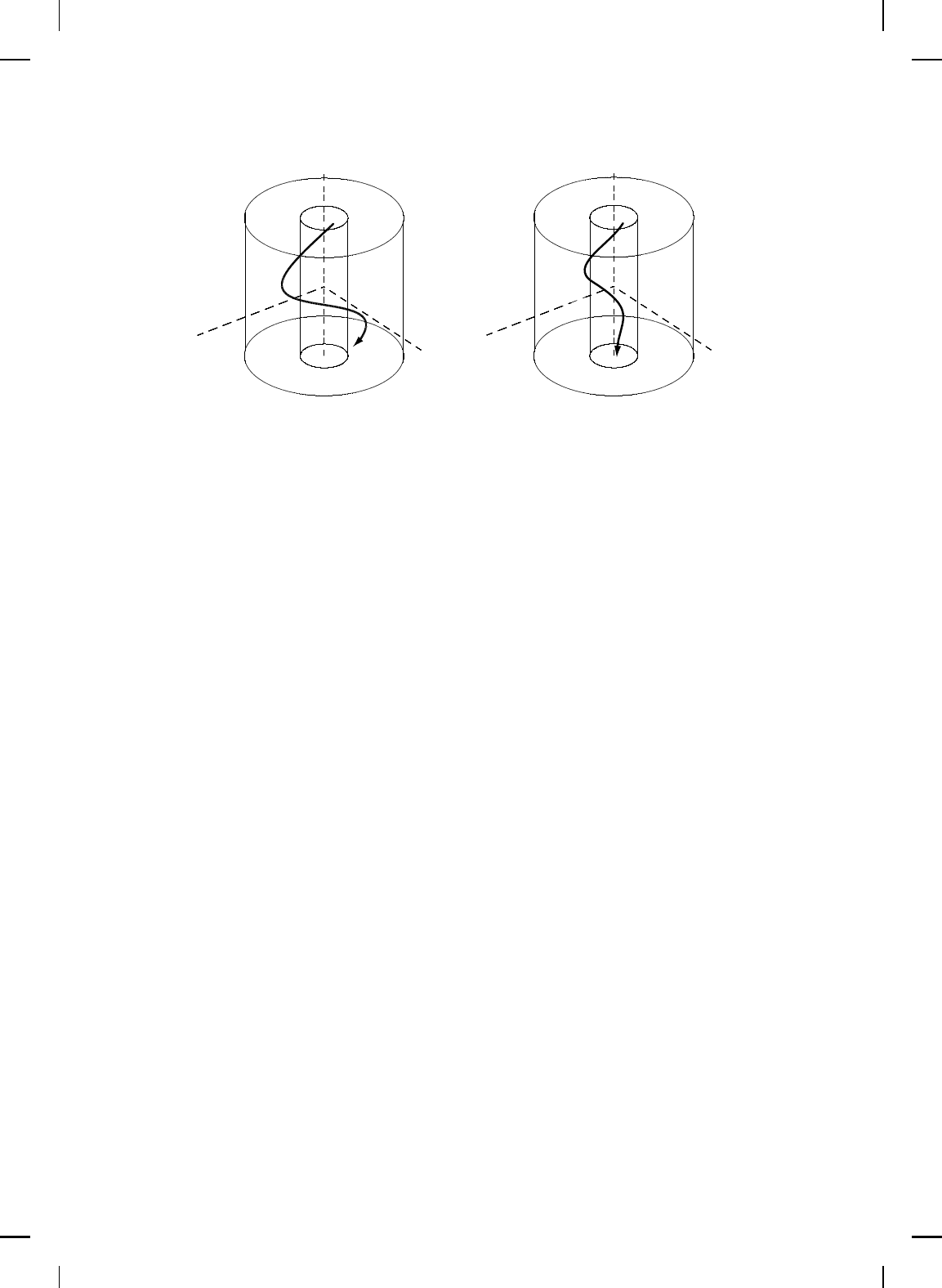
Our next example involves a nonlinear system originally studied as

a simpliﬁed model of a dual-spin spacecraft to investigate the resonance

capture phenomenon [365] and more recently was studied to investigate

the utility of a rotational/translational pr oof-mass actuator for stabilizing

translational motion [73]. The system (see Figure 4.2) involves an eccentric

rotational inertia on a translational oscillator giving rise to nonlinear

coupling between the undamped oscillator and the rotational rigid body

mode. The oscillator cart of mass M is connected to a ﬁ x ed support via

a linear spring of stiﬀness k. The cart is constrained to one-dimensional

motion and the rotational proof-mass actuator consists of a m ass m and

mass moment of inertia I located at a distance e from the cart’s center of

mass. Letting q, ˙q, θ, and

θ denote the translational position and velocity of

the cart and the angular position and velocity of the rotational pr oof mass,

respectively, the dynamic equations of m otion are given by

Figure 4.2 Rotational/translational proof-mass actuator.

(M + m)¨q(t) + me[

θ(t) cos θ(t) −

(t) sin θ(t)] + kq(t) = 0, (4.4)

(I + me

)

θ(t) + me¨q(t) cos θ(t) = 0, (4.5)

where t ≥ 0, q(0) = q

, ˙q(0) = ˙q

, θ(0) = θ

, and

θ(0) =

Note that since the motion is constrained to the horizontal plane, the

gravitational forces are not considered in the dynamic analysis. Analyzing

(4.4) and (4.5) (see Example 4.1 for details), it follows that the zero

solution (q(t), ˙q(t), θ(t),

θ(t)) ≡ (0, 0, 0, 0) to (4.4) and (4.5) is unstable in

the standard sense but partially Lyapu nov stable with respect to q, ˙q, and

(see Deﬁnition 4.1). Once again, s tandard Lyapunov stability theory cannot

be used to arrive at th is result since the angular position θ of the rotational

proof mass cannot be ignored from (4.4) and (4.5) and θ(t) → ∞ as t → ∞.

Another application of partial stability theory is the extra ﬂexibility

NonlinearBook10pt November 20, 2007

210 CHAPTER 4

it provides in constructing Lyapunov functions for nonlinear dynamical

systems. Speciﬁcally, generalizing Lyapunov’s stability theorem to include

partial s tability weakens the hypotheses on the Lyapunov function (see

Theorem 4.1) thus enlarging the class of allowable functions that can be

used in analyzing s ystem stability. Perhaps the clearest example of this is the

Lagrange-Dirichlet stability problem [368] involving the conservative E uler-

Lagrange system with a nonnegative-deﬁnite kinetic energy function T and

a positive-deﬁnite potential function U. In this case, the Lagrange-Dirichlet

energy function V = T + U is only nonnegative deﬁnite and, hence, cannot

be used as a Lyapunov fun ction candidate to analyze the stability of the

system using standard Lyapunov theory. However, the Lagrange-Dirichlet

energy function can be used as a valid L yapunov function within partial

stability theory to guarantee Lyapunov stability of the Lagrange-Dirichlet

problem (see Example 4.2).

In this section, we present partial stability theorems for nonlinear dy-

namical systems. Speciﬁcally, consider the nonlinear autonomous d ynamical

system

˙x

(t) = f

(t), x

(t)), x

(0) = x

, t ∈ I

, (4.6)

˙x

(t) = f

(t), x

(t)), x

(0) = x

, (4.7)

where x

∈ D, D ⊆ R

is an open set such that 0 ∈ D, x

∈ R

, f

D × R

→ R

is such that, for every x

∈ R

, f

(0, x

) = 0 and f

(·, x

)

is locally Lipschitz in x

, f

: D×R

→ R

is such that, for every x

∈ D,

, ·) is locally Lipschitz in x

, and I

△

= [0, τ

), 0 < τ

≤ ∞, is the

maximal interval of existence for the solution (x

(t), x

(t)), t ∈ I

, to (4.6)

and (4.7). Note that u nder the above assumptions the solution (x

(t), x

(t))

to (4.6) and (4.7) exists and is unique over I

. The following deﬁnition

introduces eight types of partial stability, that is, stability with respect to

, f or the nonlinear dynamical system (4.6) and (4.7).

Deﬁnition 4.1. i) The nonlinear dynamical system (4.6) and (4.7) is

Lyapunov stable with respect to x

if, for every ε > 0 and x

∈ R

, there

exists δ = δ(ε, x

) > 0 such that kx

k < δ implies that kx

(t)k < ε for all

t ≥ 0 (see Figure 4.3(a)).

ii) The nonlinear dynamical system (4.6) and (4.7) is Lyapunov stable

with respect to x

uniformly in x

if, for every ε > 0, there exists δ =

δ(ε) > 0 such that kx

k < δ implies that kx

(t)k < ε for all t ≥ 0 and for

all x

∈ R

iii) The nonlinear dynamical system (4.6) and (4.7) is asymptotically

stable with re spect to x

if it is Lyapunov stable with respect to x

and, for

every x

∈ R

, there exists δ = δ(x

) > 0 such that kx

k < δ implies

NonlinearBook10pt November 20, 2007

ADVANCED STABILITY THEORY 211



k = δ

k = ε

x(t)



k = δ

k = ε

x(t)

(a) (b)

Figure 4.3 (a) Partial Lyapunov stability with respect to x

. ( b) Partial asymptotic

stability with respect to x

. x

= [y

]

, x

= z, and x = [x

]

that lim

t→∞

(t) = 0 (see Figure 4.3(b)).

iv) The nonlinear d ynamical system (4.6) and (4.7) is asymptotically

stable with respect to x

uniformly in x

if it is Lyapunov stable with respect

to x

uniformly in x

and there exists δ > 0 such that kx

k < δ implies

that lim

t→∞

(t) = 0 uniformly in x

and x

for all x

∈ R

v) The nonlinear dynamical system (4.6) and (4.7) is globally asymp-

totically stable with respect to x

if it is Lyapunov stable with respect to x

and lim

t→∞

(t) = 0 for all x

∈ R

and x

∈ R

vi) The n on linear dynamical system (4.6) and (4.7) is globally asymp-

totically stable with re spect to x

uniformly in x

if it is Lyapun ov stable

with respect to x

uniformly in x

and lim

t→∞

(t) = 0 uniformly in x

and x

for all x

∈ R

and x

∈ R

vii) The nonlinear dynamical system (4.6) and (4.7) is exponentially

stable with respect to x

uniformly in x

if there exist scalars α, β, δ > 0 such

that kx

k < δ implies that kx

(t)k ≤ αkx

−βt

, t ≥ 0, for all x

∈ R

viii) The nonlinear dynamical system (4.6) and (4.7) is globally

exponentially stable with respect to x

uniformly i n x

if there exist scalars

α, β > 0 such that kx

(t)k ≤ αkx

−βt

, t ≥ 0, for all x

∈ R

and

∈ R

Next, we present suﬃcient conditions for partial stability of the

nonlinear dynamical system (4.6) and (4.7). For the following result deﬁne

V (x

, x

)

△

= V

′

, x

)f(x

, x

), where f (x

, x

)

△

= [f

, x

) f

, x

)]

NonlinearBook10pt November 20, 2007

212 CHAPTER 4

for a given continuously diﬀerentiable f unction V : D × R

→ R.

Furth ermore, we assume that the solution (x

(t), x

(t)) to (4.6) and (4.7)

exists and is unique for all t ≥ 0. It is important to note that unlike standard

theory (see Corollary 2.5) th e existence of a Lyapunov function V (x

, x

)

satisfying the conditions in Theorem 4.1 below is not suﬃcient to ensure

that all solutions of (4.6) and (4.7) starting in D × R

can be extended to

inﬁnity, since none of the states of (4.6) and (4.7) serve as an independent

variable. We do note, however, that Lipschitz continuity of f

(·, ·) and f

(·, ·)

provides a suﬃcient condition for the existence and uniqueness of solutions

to (4.6) and (4.7) over a forward time interval.

Theorem 4.1. Consider the nonlinear dynamical system (4.6) and

(4.7). Then the following statements hold:

i) I f there exist a continuous ly diﬀerentiable function V : D × R

→ R

and a class K function α(·) such that

V (0, x

) = 0, x

∈ R

, (4.8)

α(kx

k) ≤ V (x

, x

), (x

, x

) ∈ D × R

, (4.9)

V (x

, x

) ≤ 0, (x

, x

) ∈ D × R

, (4.10)

then the nonlinear dynamical system given by (4.6) and (4.7) is

Lyapunov s table with respect to x

ii) If there exist a continuously diﬀerentiable fun ction V : D × R

→ R

and class K functions α(·), β(·) satisfying (4.9), (4.10), and

V (x

, x

) ≤ β(kx

k), (x

, x

) ∈ D × R

, (4.11)

then the nonlinear dynamical system given by (4.6) and (4.7) is

Lyapunov s table with respect to x

uniformly in x

iii) If there exist continuously diﬀerentiable functions V : D × R

→ R

and W : D ×R

→ R, and class K functions α(·), β(·), and γ(·) such

that

W (x

(·), x

(·)) is bounded from below or above, (4.8) and (4.9)

hold, and

W (0, x

) = 0, x

∈ R

, (4.12)

β(kx

k) ≤ W (x

, x

), (x

, x

) ∈ D × R

, (4.13)

V (x

, x

) ≤ −γ(W (x

, x

)), (x

, x

) ∈ D × R

, (4.14)

then the nonlinear dynamical system given by (4.6) and (4.7) is

asymptotically stable with respect to x

iv) If there exist a continuously diﬀerentiable function V : D × R

→ R

and class K functions α(·), β(·), γ(·) s atisfying (4.9), (4.11), and

V (x

, x

) ≤ −γ(kx

k), (x

, x

) ∈ D × R

, (4.15)

NonlinearBook10pt November 20, 2007

ADVANCED STABILITY THEORY 213

then the nonlinear dynamical system given by (4.6) and (4.7) is

asymptotically stable with respect to x

uniformly in x

v) If D = R

and there exist continuously diﬀerentiable functions V :

× R

→ R and W : R

× R

→ R, class K functions β(·), γ(·),

and a class K

∞

function α(·) such that

W (x

(·), x

(·)) is bounded

from below or above, and (4.8), (4.9), and (4.12)–(4.14) hold, then

the nonlinear dynamical system given by (4.6) and (4.7) is globally

asymptotically stable with respect to x

vi) If D = R

and there exist a continuously diﬀerentiable function

V : R

× R

→ R, a class K function γ(·), and class K

∞

functions

α(·), β(·) satisfying (4.9), (4.11), and (4.15), then the nonlinear

dynamical system given by (4.6) and (4.7) is globally asymptotically

stable with respect to x

uniformly in x

vii) If there exist a continuously diﬀerentiable function V : D × R

→ R

and positive constants α, β, γ, p ≥ 1 satisfying

αkx

≤ V (x

, x

) ≤ βkx

, (x

, x

) ∈ D × R

, (4.16)

V (x

, x

) ≤ −γkx

, (x

, x

) ∈ D × R

, (4.17)

then the nonlinear dynamical system given by (4.6) and (4.7) is

exponentially stable with respect to x

uniformly in x

viii) If D = R

and there exist a continuously diﬀerentiable function V :

× R

→ R and positive constants α, β, γ, p ≥ 1 satisfying (4.16)

and (4.17), then the nonlinear dynamical system given by (4.6) and

(4.7) is globally exponentially stable with respect to x

uniformly in

Proof. i) Let x

∈ R

, let ε > 0 be such that B

(0)

△

= {x

∈

: kx

k < ε} ⊂ D, deﬁne η

△

= α(ε), and deﬁne D

△

= {x

∈ B

(0) :

V (x

, x

) < η}. Since V (·, ·) is continuous and V (0, x

) = 0 it follows that

is nonempty and there exists δ = δ(ε, x

) > 0 such that V (x

, x

) < η,

∈ B

(0). Hence, B

(0) ⊆ D

. Next, since

V (x

, x

) ≤ 0 it follows

that V (x

(t), x

(t)) is a nonincreasing function of time, and h en ce, for every

∈ B

(0) ⊆ D

it follows that

α(kx

(t)k) ≤ V (x

(t), x

(t)) ≤ V (x

, x

) < η = α(ε).

Thus , for every x

∈ B

(0) ⊆ D

, x

(t) ∈ B

(0), t ≥ 0, establishing

Lyapunov s tability with respect to x

ii) Let ε > 0 and let B

(0) and η be given as in the proof of i). Now,

let δ = δ(ε) > 0 be such that β(δ) = α(ε). Then it follows from (4.11) that

NonlinearBook10pt November 20, 2007

214 CHAPTER 4

for all (x

, x

) ∈ B

(0) ×R

α(kx

(t)k) ≤ V (x

(t), x

(t)) ≤ V (x

, x

) < β(δ) = α(ε),

and h en ce, x

(t) ∈ B

(0), t ≥ 0.

iii) Lyapunov stability follows from i). To show asymptotic stability

suppose, ad absurdum, that W (x

(t), x

(t)) 9 0 as t → ∞ or, equivalently,

lim sup

t→∞

W (x

(t), x

(t)) > 0. In addition, suppose lim inf

t→∞

W (x

(t),

(t)) > 0, which implies that there exist constants T > 0 and k > 0

such that W (x

(t), x

(t)) ≥ k, t ≥ T . Then it follows from (4.14) that

V (x

(t), x

(t)) → −∞ as t → ∞, which contradicts (4.9), and hence,

lim inf

t→∞

W (x

(t), x

(t)) = 0. Now, since lim sup

t→∞

W (x

(t), x

(t)) > 0

and lim inf

t→∞

W (x

(t), x

(t)) = 0 it follows that there exist two increasing

sequences {t

}

∞

i=0

and {t

′

}

∞

i=0

, and a constant k > 0 such that t

< t

′

< t

i+1

i = 0, 1, . . ., t

→ ∞ as i → ∞, and

W (x

), x

)) =

< W (x

(t), x

(t)) < k = W (x

′

), x

′

)),

< t < t

′

, i = 0, 1, . . . . (4.18)

Furth ermore, since

W (x

(·), x

(·)) is upper (respectively, lower) bounded

there exists η > 0 (respectively, η < 0) such that

W (x

(t), x

(t)) ≤ η, t ≥ 0

(respectively,

W (x

(t), x

(t)) ≥ η, t ≥ 0). In the case where

W (x

(·), x

(·))

is upper bounded it follows from (4.18) that t

′

− t

≥

2η

, i = 1, 2, . . ., and

hence,

′

γ(W (x

(t), x

(t)))dt ≥ γ(

)

2η

. Now, using (4.14), it follows that

V (x

′

), x

′

)) = V (x

, x

) +

V (x

(t), x

(t))dt

i=1

′

V (x

(t), x

(t))dt

n−1

i=1

i+1

′

V (x

(t), x

(t))dt

≤ V (x

, x

) +

i=1

′

V (x

(t), x

(t))dt

≤ V (x

, x

) −

i=1

′

γ(W (x

(t), x

(t)))dt

≤ V (x

, x

) −nγ





2η

. (4.19)

Hence, for suﬃciently large n the right-hand side of (4.19) becomes negative,

which contradicts (4.9). The case where

W (x

(·), x

(·)) is lower bounded

leads to a similar contradiction using identical arguments. Thus, in either