Haddad W.M. Nonlinear Dynamical Systems and Control: A Lyapunov-Based Approach

Подождите немного. Документ загружается.

NonlinearBook10pt November 20, 2007

ADVANCED STABILITY THEORY 285

holds. Then it follows that x(t) ∈ O

, t ≥ 0, and hence, it follows from

Theorem 2.41 that the positive limit set ω(x

) of x(t), t ≥ 0, is a nonempty,

compact, invariant, and connected set. Furthermore, x(t) → ω(x

) as t →

∞. Now, since V (x(t)), t ≥ 0, is non increasing and bounded from below by

zero it follows that β

△

= lim

t→∞

V (x(t)) ≥ 0 is well deﬁned. Furthermore,

since V (·) is lower s emicontinuous it can be shown that V (y) ≤ β, y ∈ ω(x

and hence, since V (·) is nonnegative, β = 0 if and only if ω(x

) = D

or,

equivalently, x(t) → D

as t → ∞. Now, sup pose, ad absurdum, that

x(t), t ≥ 0, does not converge to D

or, equivalently, β > 0. Furthermore,

let y ∈ ω(x

) and let {τ

}

∞

n=0

be an increasing unbounded sequence such that

lim

n→∞

x(τ

) = y. Since {V (x(τ

))}

∞

n=0

is a lower bounded nonincreasing

sequence, lim

n→∞

V (x(τ

)) exists and is equal to β. Hence, y 6∈ D

and

since y ∈ ω(x

) is arbitrary, it follows that ω(x

) ∩ D

= Ø. Next, let

△

= min

x∈ω(x

)

V (x) > 0 and let x

∈ ω(x

) be such that V (x

) = γ.

Now, since ω(x

) is an invariant set it follows that for all x(0) ∈ ω(x

x(t) ∈ ω(x

), t ≥ 0, and hence, V (x(t)) ≥ γ, t ≥ 0. However, since for all

x(0) ∈ D, x(0) 6∈ D

, there exists an increasing unbounded sequence {t

}

∞

n=1

such that (4.256) holds, it follows that if x(0) = x

∈ ω(x

), there exists

t > 0 s uch that V (x(t)) < V (x(0)) = γ, which is a contradiction. Hence,

ω(x

) ⊆ D

and x(t) → D

as t → ∞, establishing asymptotic stability.

Note that in the case where the function V (·) is continuously

diﬀerentiable on D in Theorem 4.29, it follows that V (x(t)) ≤ V (x(τ)), for

all t ≥ τ ≥ 0, is equivalent to

V (x)

△

= V

′

(x)f(x) ≤ 0, x ∈ D. Furthermore,

V (x) = V

′

(x)f(x) < 0, x ∈ D, x 6∈ D

, then every increasing unbounded

sequence {t

}

∞

n=0

, with t

= 0, is su ch that V (x(t

n+1

)) < V (x(t

)), n =

0, 1, . . .. Hence, the following corollary to Theorem 4.29 is immediate.

Corollary 4.7. Consider the nonlinear dynamical system (4.251) and

let D

be a compact positively invariant set with respect to (4.251) such th at

⊂ D. Assume that there exists a continuously diﬀerentiable function

V : D → R such that

V (x) = 0, x ∈ D

, (4.257)

V (x) > 0, x ∈ D, x 6∈ D

, (4.258)

′

(x)f(x) ≤ 0, x ∈ D. (4.259)

Then D

is Lyapunov stable. I f, in addition,

′

(x)f(x) < 0, x ∈ D, x 6∈ D

, (4.260)

then D

is asymptotically stable.

The following theorem provides a converse to Theorem 4.29. For this

result deﬁn e the notation D

△

= {x ∈ D : dist(x, D

) < r}, r > 0, to denote

an r open neighborhood of D

NonlinearBook10pt November 20, 2007

286 CHAPTER 4

Theorem 4.30. Consider the nonlinear dynamical system (4.251). If

is Lyapunov stable, then there exist D

⊆ D and a lower semicontinuous,

positive-deﬁnite (on D

) function V : D

→ R such that D

⊂

◦

, V (·)

is continuous on D

, and

V (s(t, x)) ≤ V (s(τ, x)), 0 ≤ τ ≤ t, x ∈ D

. (4.261)

If D

is asymptotically stable, then there exists a continuous, positive-

deﬁnite function V : D

→ R such that inequality (4.261) is strictly satisﬁed.

Proof. Let ε > 0. Since D

is Lyapunov stable it follows that there

exists δ = δ(ε) > 0 such that if x

∈ D

, then s(t, x

) ∈ D

, t ≥ 0. Now,

let D

△

= {y ∈ D

: there exists t ≥ 0 and x

∈ D

such that y = s(t, x

)}.

Note that D

⊆ D

, D

is a positively invariant set, and D

⊆ D

. Hence,

⊂

◦

. Next, deﬁne V (x)

△

= sup

t≥0

dist(s(t, x), D

), x ∈ D

, and since D

is positively invariant and bounded it follows that V (·) is well deﬁned on D

Now, since D

is invariant, x ∈ D

implies V (x) = 0, x ∈ D

. Furth ermore,

V (x) ≥ dist(s(0, x), D

) > 0, x ∈ D

, x 6∈ D

Next, since f (·) in (4.251) is such that for every x ∈ D

, s(t, x), t ≥ 0,

is the unique solution to (4.251), it follows that s(t, x) = s(t−τ, s(τ, x)), 0 ≤

τ ≤ t. Hence, f or every t, τ ≥ 0, such th at t ≥ τ ,

V (s(τ, x)) = sup

θ≥0

dist(s(θ, s(τ, x)), D

)

= sup

θ≥0

dist(s(τ + θ, x), D

)

≥ sup

θ≥t−τ

dist(s(τ + θ, x), D

)

= sup

θ≥t−τ

dist(s(θ − (t − τ), s(t, x)), D

)

= sup

θ≥0

dist(s(θ, s(t, x)), D

)

= V (s(t, x)), (4.262)

which proves (4.261). Next, let p

∈ D

. Since D

is Lyapunov stable

it follows that for every ˆε > 0 there exists

δ =

δ(ε) > 0 such that if

∈ B

), then s(t, x

) ∈ D

ˆε/2

, t ≥ 0, which implies that V (x

) =

sup

t≥0

dist(s(t, x

), D

) ≤

ˆε

. Hence, for every point p

∈ D

and ˆε > 0

there exists

δ =

δ(ˆε) such that if x

∈ B

), th en V (x

) < ˆε, establishing

that V (·) is continuous on D

Finally, to show that V (·) is lower semicontinuous everywhere on D

let x ∈ D

, let ˆε > 0, and note that since V (x)

△

= sup

t≥0

dist(s(t, x), D

there exists T = T (x, ˆε) > 0 such that V (x) − dist(s(T, x), D

) < ˆε. Now,

consider a sequence {x

}

∞

i=1

∈ D

such that x

→ x as i → ∞. Next, since

NonlinearBook10pt November 20, 2007

ADVANCED STABILITY THEORY 287

s(t, ·) is continuous for every t ≥ 0 and dist(·, D

) : D

→ R is continuous,

it f ollows that dist(s(T, x), D

) = lim

i→∞

dist(s(T, x

), D

). Next, note that

dist(s(T, x

), D

) ≤ sup

t≥0

dist(s(t, x

), D

), i = 1, 2, . . ., and hence,

lim inf

i→∞

sup

t≥0

dist(s(t, x

), D

) ≥ lim inf

i→∞

dist(s(T, x

), D

)

= lim

i→∞

dist(s(T, x

), D

), i = 1, 2, . . . ,

which implies that

V (x) < dist(s(T, x), D

) + ˆε

= lim

i→∞

dist(s(T, x

), D

) + ˆε

≤ lim inf

i→∞

sup

t≥0

dist(s(t, x

), D

) + ˆε

= lim inf

i→∞

V (x

) + ˆε. (4.263)

Now, since ˆε > 0 is arbitrary, (4.263) implies that V (x) ≤ lim inf

i→∞

V (x

Thus , since {x

}

∞

i=1

is an arbitrary sequence converging to x, it follows that

V (·) is lower semicontinuous on D

To show the existence of a continuous, positive-deﬁnite, strictly

decreasing function along th e system trajectories of (4.251) in the case where

is asymptotically stable, consider the function V : D

→ R given by

V (x)

△

∞

sup

t≥0

dist(s(t, s(σ, x)), D

−σ

dσ, x ∈ D

, (4.264)

where D

⊆ D

is a domain of attraction of D

. Since D

is asymptotically

stable, it follows that

V (x)

△

= sup

t≥0

dist(s(t, x), D

), x ∈ D

, is continuous

on D

(see [58, p. 67]), which implies that V (·) is continuous on D

and

positive deﬁnite on D

\ D

. Next, sup pose, ad absurdum, that

V (s(t, x)) = V (s(τ, x)), (4.265)

for some 0 ≤ τ < t and x ∈ D

. Now, since

V (·) is positive deﬁnite (on

\ D

) and (4.261) holds for

V (·), (4.265) implies that

V (s(σ + t, x)) =

V (s(σ + τ, x)) for all σ ≥ 0. However, since D

is asymptotically stable

it follows that dist(s(t, x), D

) → 0 as t → ∞ for x ∈ D

, and h en ce, for

suﬃciently large σ

∗

> 0, dist(s(σ

∗

+t, x), D

) < dist(s(σ

∗

+τ, x), D

). Thus,

V (s(σ

∗

+ t, x)) <

V (s(σ

∗

+ τ, x)), which leads to a contradiction. Hence,

inequality (4.261) is strictly satisﬁed f or V (·) which completes the proof.

Next, we generalize the Barbashin-Krasovskii-LaSalle invariant set

theorems to the case in which the function V (·) is lower semicontinuous.

In particular, we show that the system trajectories converge to a union of

largest invariant sets contained on the bou ndary of the intersections over

ﬁnite intervals of the closure of generalized Lyapunov level surfaces. For the

NonlinearBook10pt November 20, 2007

288 CHAPTER 4

remainder of the results of this section deﬁne the n otation

△

c>γ

−1

([γ, c]), (4.266)

for arbitrary V : D ⊆ R

→ R and γ ∈ R, and let M

denote the largest

invariant set (with respect to (4.251)) contained in R

Theorem 4.31. Consider the nonlinear dynamical system (4.251), let

and D

be compact positively invariant sets with respect to (4.251) such

that D

⊂ D

⊂ D, and let x(t), t ≥ 0, denote the solution to (4.251)

corresponding to x

∈ D

. Assume that there exists a lower semicontinuous

function V : D

→ R such that

V (x) = 0, x ∈ D

, (4.267)

V (x) > 0, x ∈ D

, x 6∈ D

, (4.268)

V (x(t)) ≤ V (x(τ)), 0 ≤ τ ≤ t. (4.269)

Furth ermore, assum e that for all x

∈ D

, x

6∈ D

, th ere exists an increasing

unbounded sequence {t

}

∞

n=0

, with t

= 0, such th at

V (x(t

n+1

)) < V (x(t

)), n = 0, 1, . . . . (4.270)

Then, either M

⊂

△

= R

\ V

−1

(γ), or M

= Ø, γ > 0. Furthermore,

if x

∈ D

, then x(t) →

△

= ∪

γ∈G

as t → ∞, where G

△

= {γ ≥ 0 :

∩ D

6= Ø}. If, in addition, D

⊂

◦

and V (·) is continuous on D

then D

is locally asymptotically stable and D

is a subset of the domain of

attraction.

Proof. Sin ce D

is a compact positively invariant s et, it follows that for

all x

∈ D

, the forward solution x(t), t ≥ 0, to (4.251) is bounded. Hence,

it follows from Theorem 2.41 that, for all x

∈ D

, ω(x

) is a nonempty,

compact, connected invariant set. Next, it follows from Theorem 4.24 and

the fact that V (·) is positive deﬁnite (with respect to D

\ D

), that for

every x

∈ D

there exists γ

≥ 0 such that ω(x

) ⊆ M

⊆ R

. Now,

given x(0) ∈ V

−1

(γ

), γ

> 0, (4.270) implies that there exists t

> 0

such that V (x(t

)) < γ

and x(t

) 6∈ V

−1

(γ

). Hence, V

−1

(γ

) ⊂ R

does not contain any invariant set. Alternatively, if x(0) ∈

, then

V (x(0)) < γ

and (4.270) implies that x(t) 6∈ V

−1

(γ

), t ≥ 0. Hence,

any invariant set contained in R

is a subset of

, w hich implies that

⊂

, γ

> 0. If ˆγ > 0 is such that ˆγ 6= γ

for all x

∈ D

then there does not exist x

∈ D

such that ω(x

) ⊆ R

ˆγ

, and hence, M

ˆγ

Ø. Now, ad absurdum, suppose D

∩ ω(x

) = Ø. Since V (·) is lower

semicontinuous it follows from Theorem 2.11 that there exists ˆx ∈ ω(x

)

such that α = V (ˆx) ≤ V (x), x ∈ ω(x

). Now, with x(0) = ˆx 6∈ D

it follows

from (4.270) that there exists an increasing unbounded sequence {t

}

∞

n=0

NonlinearBook10pt November 20, 2007

ADVANCED STABILITY THEORY 289

with t

= 0, such that V (x(t

n+1

)) < V (x(t

)), n = 0, 1, . . ., which implies

that there exists t > 0 such that V (x(t)) < α, and hence, x(t) 6∈ ω(x

contradicting the fact that ω(x

) is an invariant set. Hence, there exists

q ∈ D

such that q ∈ ω(x

) ⊆ R

, which implies that R

∩ D

6= Ø.

Thus , γ

∈ G for all x

∈ D

, which further implies that ω(x

) ⊆

M. Now,

since x(t) → ω(x

) ⊆

M as t → ∞ it follows that x(t) →

M as t → ∞.

If V (·) is continuous on D

⊂

◦

, then Lyapunov stability of the com-

pact positively invariant set D

follows from Theorem 4.29. Furthermore,

from the continuity of V (·) on D

and the fact that V (x) = 0 for all x ∈ D

it follows th at G = {0} and

M ≡ M

. Hence, ω(x

) ⊆ D

for all x

∈ D

establishing local asymptotic stability of the compact positively invariant

set D

of (4.251) with a subset of the domain of attraction given by D

Finally, we present a generalized global invariant set theorem for

guaranteeing global attraction and global asymptotic stability of a compact

positively invariant set of a nonlinear dynamical system.

Theorem 4.32. Consider the nonlinear dynamical system (4.251) with

D = R

and let x(t), t ≥ 0, denote the solution to (4.251) corresponding

to x

∈ R

. Assume that there exists a compact positively invariant set D

with respect to (4.251) and a lower semicontinuous function V : R

→ R

such that

V (x) = 0, x ∈ D

, (4.271)

V (x) > 0, x ∈ R

, x 6∈ D

, (4.272)

V (x(t)) ≤ V (x(τ)), 0 ≤ τ ≤ t, (4.273)

V (x) → ∞ as kxk → ∞. (4.274)

Then for all x

∈ R

, x(t) → M

△

= ∪

γ≥0

, as t → ∞. If, in addition,

for all x

∈ R

, x

6∈ D

, there exists an increasing unbounded sequence

}

∞

n=0

, with t

= 0, such th at

V (x(t

n+1

)) < V (x(t

)), n = 0, 1, . . . , (4.275)

then, either M

⊂

△

= R

\ V

−1

(γ), or M

= Ø, γ > 0. Furthermore,

x(t) →

△

= ∪

γ∈G

as t → ∞, where G

△

= {γ ≥ 0 : R

∩ D

6= Ø}.

Finally, if V (·) is continuous on D

then the compact positively invariant

set D

of (4.251) is globally asymptotically stable.

Proof. Note that since V (x) → ∞ as kxk → ∞ it follows that for every

β > 0 there exists r > 0 such that V (x) > β for all kxk> r or, equivalently,

−1

([0, β]) ⊆ {x : kxk ≤ r}, which implies that V

−1

([0, β]) is bounded for

all β > 0. Hence, for all x

∈ R

, V

−1

([0, β

]) is bounded, where β

△

NonlinearBook10pt November 20, 2007

290 CHAPTER 4

V (x

). Furthermore, since V (·) is a positive-deﬁnite lower semicontinuous

function, it follows that V

−1

([0, β

]) is closed an d, s ince V (x(t)), t ≥ 0, is

nonincreasing, V

−1

([0, β

]) is positively invariant. Hence, for every x

∈

, V

−1

([0, β

]) is a compact positively invariant set. Now, with D

−1

([0, β

]) it f ollows from Theorem 4.24 that there exists γ

∈ [0, β

]

such that ω(x

) ⊆ M

⊂

, which implies that x(t) → M as t → ∞.

If, in addition, for all x

∈ R

, x

6∈ D

, there exists an increasing unbounded

sequence {t

}

∞

n=0

, with t

= 0, such that (4.275) holds, then it follows from

Theorem 4.31 that x(t) →

M as t → ∞.

Finally, if V (·) is continuous on D

then Lyapunov stability follows as

in the proof of Theorem 4.31. Fu rthermore, in this case, G = {0}, which

implies that

M = M

. Hence, ω(x

) ⊆ D

, establishing global asymptotic

stability of the compact positively invariant set D

of (4.251).

4.10 Poincar´e Maps and S tability of Periodic Orbits

Poincar´e’s theorem [358] provides a powerful tool in analyzing the stability

properties of periodic orbits and limit cycles of n-dimensional dynamical

systems in the case where the trajectory of the system can be relatively easily

integrated. Speciﬁcally, Poincar´e’s theorem provides necessary and suﬃcient

conditions for stability of periodic orbits based on the stability properties of a

ﬁxed point of a discrete-time dynamical system constructed from a Poincar´e

return map. In particular, for a given candidate periodic trajectory, an (n −

1)-dimensional hyperplane is constructed that is transversal to the periodic

trajectory and which deﬁnes th e Poincar´e return map. Trajectories starting

on the hyperplane which are suﬃciently close to a point on the periodic

orbit will intersect the hyp erplane after a time approximately equal to the

period of the periodic orbit. This mapping traces the system trajectory

from a point on the hyperplane to its next corresponding intersection with

the hyperplane. Hence, the Poincar´e retur n map can be used to establish

a relationship between the stability properties of a dynamical sys tem with

periodic solutions and the stability properties of an equilibrium point of

an (n − 1)-dimensional discrete-time system. In this section, using the

notions of Lyapunov and asymptotic stability of sets developed in S ection

4.9, we construct lower semicontinuous Lyapunov functions to provide a

Lyapunov f unction proof of Poincar´e’s th eorem. To begin, we introduce

the notions of Lyapunov and asymptotic stability of a periodic orbit of the

nonlinear dynamical system (4.251). For this deﬁnition recall the deﬁnitions

of periodic solutions and periodic orbits of (4.251) given in Deﬁnition 2.53.

Deﬁnition 4.12. A periodic orbit O of (4.251) is Lyapunov stable if,

for all ε > 0, there exists δ = δ(ε) > 0 such that if dist(x

, O) < δ, then

dist(s(t, x

), O) < ε, t ≥ 0. A periodic orbit O of (4.251) is asymptotically

NonlinearBook10pt November 20, 2007

ADVANCED STABILITY THEORY 291

stable if it is Lyapunov stable and there exists δ > 0 such that if dist(x

, O) <

δ, then dist(s(t, x

), O) → 0 as t → ∞.

To proceed, we assume that for the point p ∈ D, the dynamical system

(4.251) has a periodic solution s(t, p), t ≥ 0, with period T > 0 that generates

the periodic orbit O

△

= {x ∈ D : x = s(t, p), 0 ≤ t ≤ T }. Note th at

O is a compact invariant set. Fur th ermore, we assume that there exists

a continuously diﬀerentiable function X : D → R such that the (n − 1)-

dimensional hyperplane deﬁned by H

△

= {x ∈ D : X(x) = 0} contains the

point x = p and X

′

(p) 6= 0. In addition, we assume that the hyperplane

H is not tangent to the periodic orbit O at x = p, that is, X

′

(p)f(p) 6= 0.

Next, deﬁne the local section S ⊂ H such that p ∈ S, X

′

(x) 6= 0, x ∈ S, and

no trajectory of (4.251) starting in S is tangent to H, that is, X

′

(x)f(x) 6=

0, x ∈ S. Note that a trajectory s(t, p) will intersect S at p in T seconds.

Furth ermore, let

△

= {x ∈ S : there exists ˆτ > 0 such that s(ˆτ , x) ∈ S

and s(t, x) 6∈ S, 0 < t < ˆτ}, (4.276)

and let τ : U → R

be deﬁned by

τ(x)

△

= {ˆτ > 0 : s(ˆτ, x) ∈ S and s(t, x) 6∈ S, 0 < t < ˆτ}. (4.277)

Finally, deﬁne the Poincar´e return map P : U → S by

P (x)

△

= s(τ (x), x), x ∈ U. (4.278)

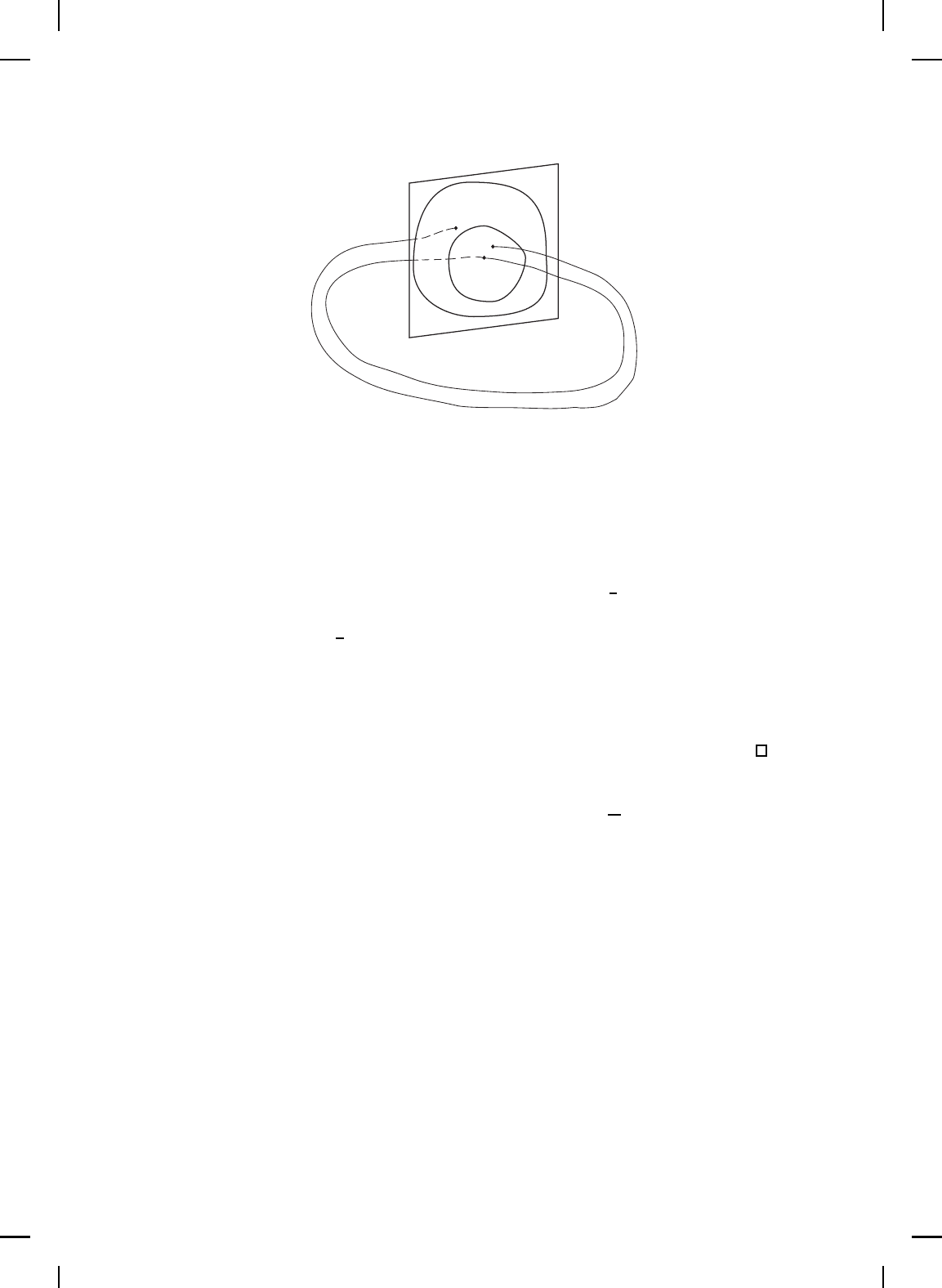
Figure 4.9 gives a visualization of the Poincar´e retur n map construction.

Next, deﬁne D

△

= {x ∈ D : there exists τ(x) > 0 such that s(τ(x),

x) ∈ S} and note that, for every x ∈ O, there exists δ = δ(x) > 0 such

that B

(x) ⊂ D

, and hence, O ⊂

◦

. S imilarly, deﬁne O

△

= {x ∈ D

s(τ(x), x) ∈ S

} and U

△

= {x ∈ S

: s(τ(x), x) ∈ S

}, where S

△

= B

(p)∩S,

α > 0, and O ⊂

◦

⊆ D

. T he function τ : D

→ R

deﬁnes the minimum

time required for the trajectory s(t, x), x ∈ D

, to return to the local section

S. Note that τ (x) > 0, x ∈ U. The following lemma shows that τ (·) is

continuous on

◦

\H.

Lemma 4.4. Consider the nonlinear dynamical system (4.251). As-

sume that the point p ∈ D

generates the periodic orbit O

△

= {x ∈ D

: x =

s(t, p), 0 ≤ t ≤ T }, where s(t, p), t ≥ 0, is the periodic solution with period

T ≡ τ(p). Then the function τ :

◦

→ R

is continuous on

◦

\H.

Proof. Let ε > 0 and x ∈

◦

\H. Note that x

∗

△

= s(τ(x), x) ∈ S, and

hence, X

′

∗

) 6= 0 and X

′

∗

)f(x

∗

) 6= 0. Now, since s(·, x) is continuous in

NonlinearBook10pt November 20, 2007

292 CHAPTER 4

P (x)

Figure 4.9 Visualization of the Poincar´e return map.

t, [0, t

] is a compact interval it follows from the d eﬁ nition of τ(·) that there

exists

t > 0 such that for every t

∈ (

t, τ(x)),

σ(t

)

△

= inf

0≤t≤t

dist(s(t, x), S) > 0. (4.279)

Next, for suﬃciently small ˆε > 0, deﬁne t

△

= τ(x) +

ˆε

and x

△

= s(t

, x).

Since X

′

∗

) 6= 0 and X

′

∗

)f(x

∗

) 6= 0, it follows that dist(x

, S) > 0. Now,

deﬁne t

△

= τ(x) −

ˆε

. Then it follows from the continuous dependence of

solutions to (4.251) in time and initial data that there exists δ > 0 such

that for all y ∈ B

(x), sup

≤t≤t

ks(t, y) − s(t, x)k < min{dist(x

, S), σ(t

)}.

Hence, for all y ∈ B

(x), it follows that t

< τ(y) < t

. Now, taking

ˆε < ε, it follows that |τ(y) −τ (x)| < ε, establishing the continuity of τ(·) at

x ∈

◦

\H.

Finally, deﬁne the discrete-time dynamical system given by

z(k + 1) = P (z(k)), z(0) ∈ U, k ∈ Z

. (4.280)

Clearly x = p is a ﬁxed point of (4.280) since T = τ(p), an d h en ce, p = P (p).

Since Poincar´e’s theorem provides necessary and suﬃcient conditions for

stability of periodic orbits based on the stability properties of a ﬁxed

point of the discrete-time dynamical sy s tem (4.280), stability notions of

discrete-time systems are required. Chapter 13 develops stability theory

for discrete-time s y s tems. Rather than embarking on a lengthy discussion

of discrete-time stability theory, here we give two key necessary results

for developing Poincar´e’s theorem. For th ese results, the deﬁnitions of

Lyapunov and asymptotic stability of a discrete-time system are analogous

to their continuous-time counterparts and are given in Chapter 13 (see

Deﬁnition 13.1). First, we note that if ρ(P

′

(z(p))) < 1, where ρ(·)

denotes the spectral radius, then the ﬁxed point x = p of th e nonlinear

NonlinearBook10pt November 20, 2007

ADVANCED STABILITY THEORY 293

discrete-time dynamical system (4.280) is asymptotically stable. This is

Lyapunov’s indirect method for nonlinear discrete-time systems. For d etails,

see Problem 13.10. Second, the following theorem is a direct application of

the standard discrete-time Lyapunov stability theorem (see Theorems 13.2

and 13.6) for general nonlinear dynamical systems to the dynamical system

(4.280).

Theorem 4.33. The equilibrium solution z(k) ≡ p to (4.280) is

Lyapunov (respectively, asymptotically) stable if and only if there exist

a scalar α > 0 and a lower semicontinuous (respectively, continuous)

function V : S

→ R such that V (·) is continuous at x = p, V (p) = 0,

V (x) > 0, x ∈ S

, x 6= p, and V (P (x)) − V (x) ≤ 0, x ∈ U

(respectively,

V (P (x)) −V (x) < 0, x ∈ U

, x 6= p).

Next, we present Poincar´e’s stability th eorem.

Theorem 4.34. Consider the nonlinear dynamical system (4.251) with

the Poincar´e map deﬁned by (4.278). Assume that the point p ∈ D generates

the periodic orbit O

△

= {x ∈ D : x = s(t, p), 0 ≤ t ≤ T }, where s(t, p), t ≥ 0,

is the perio dic solution with period T ≡ τ(p). Then the following statements

hold:

i) p ∈ D is a Lyapunov stable ﬁxed point of (4.280) if and only if the

periodic orbit O generated by p is Lyapunov stable.

ii) p ∈ D is an asymptotically stable ﬁxed point of (4.280) if and only if

the periodic orbit O generated by p is asymptotically stable.

Proof. i) To s how necessity, assume that x = p is a Lyapunov stable

ﬁxed point of (4.280). Then it follows from Theorem 4.33 that for suﬃciently

small α > 0 there exists a lower semicontinuous function V

: S

→ R such

that V

(·) is continuous at x = p, V

(p) = 0, V

(x) > 0, x ∈ S

, x 6= p, and

(P (x))−V

(x) ≤ 0, x ∈ U

. Next, deﬁne a function V : O

→ R such that

V (x) = V

(s(τ(x), x)), x ∈ O

. It follows from the deﬁnition of τ (·), Lemma

4.4, and the j oint continuity of solutions of (4.251) that V (·) is a lower

semicontinuous function on O

and V (x) = 0, x ∈ O, V (x) > 0, x ∈ O

\O,

where O ⊂

◦

. Alternatively, it f ollows from the Lyapunov stability of the

ﬁxed point x = p of (4.280) that for ε > 0 such th at B

(p) ∩ S ⊂ U

there exists δ = δ(ε) > 0 such that z(k) ∈ B

(p) ∩ S, k ∈ Z

, for all

z(0) ∈ B

(p) ∩ S, where z(k) ∈ N satisﬁes (4.280). Now, deﬁne O

△

= {x ∈

: s(τ(x), x) ∈ B

(p) ∩ S} and note that O ⊂

◦

. Hence, V (s(t, x)) ≤

V (s(τ, x)), 0 ≤ τ ≤ t, for every x ∈ O

⊆ O

. Now, to show that V (·) is

continuous on O let p

∈ O be such that p

6= p and consider any arbitrary

NonlinearBook10pt November 20, 2007

294 CHAPTER 4

sequence {x

}

∞

n=0

∈ O

such that lim

n→∞

= p

. Then, since τ(·) is

continuous on D

\ H, it follows that lim

n→∞

τ(x

) = τ(p

) and, by joint

continuity of solutions of (4.251), s(τ(x

), x

) → s(τ(p

), p

) = p as n →

∞. Now, since V

(·) is continuous at x = p, it follows that lim

n→∞

V (x

) =

lim

n→∞

(s(τ(x

), x

)) = V

(p) = 0, which, since {x

}

∞

n=0

is arbitrary,

implies continuity of V (·) at any point p

∈ O, p

6= p.

Next, we show the continuity of V (·) at x = p. Note, that V (·) is

not necessarily continuous at every point of S but x = p. Consider any

arbitrary sequence {x

}

∞

n=0

∈ O

such that lim

n→∞

= p. For this

sequence we have one of the following three cases: either lim

n→∞

τ(x

) = 0,

lim

n→∞

τ(x

) = T , or there exist su bsequences {x

}

∞

k=0

and {x

}

∞

m=0

such that {x

}

∞

k=0

∪ {x

}

∞

m=0

= {x

}

∞

n=0

, x

→ p, τ(x

) → 0, as

k → ∞, and x

→ p, τ(x

) → T , as m → ∞. We assume the latter

case, sin ce the analysis for the ﬁrst two cases follows immediately from the

arguments for p

∈ O, p

6= p, presented above. The characterization

of both subsequences and joint continuity of solutions of (4.251) yield

s(τ(x

), x

) → s(0, p) = p and s(τ(x

), x

) → s(T, p) = p, as k → ∞,

and m → ∞, respectively. Now, sin ce V

(·) is continuous at x = p, it

follows that lim

k→∞

V (x

) = lim

k→∞

(s(τ(x

), x

)) = V

(p) = 0 and

lim

m→∞

V (x

) = lim

m→∞

(s(τ(x

), x

)) = V

(p) = 0, and thus,

lim

n→∞

V (x

) = V (p) = 0, which implies that V (·) is continuous at x = p,

and hence, V (·) is continuous on O. Finally, since all th e assump tions of

Theorem 4.29 hold, the periodic orbit O is Lyapunov stable.

To show suﬃ ciency, assume that the periodic orbit O generated by the

point p ∈ D is Lyapunov s table. Th en it follows from the Theorem 4.30 that

there exists a lower semicontinuous, positive-deﬁnite (on D

\ O) function

V : D

→ R such that (4.261) is satisﬁed. Now, for suﬃciently small α > 0,

construct a function V

: S

→ R such that V

(x) = V (x), x ∈ S

. Thus,

in this case the suﬃcient conditions of Theorem 4.33 are satisﬁed for V

(·),

which implies that the point x = p is a Lyapunov stable ﬁxed point of

(4.280).

ii) To show necessity, assume that x = p is an asymptotically stable

ﬁxed point of (4.280). Then it follows from T heorem 4.33 that there exists

a continuous function V

: S

→ R such that V

(p) = 0, V

(x) > 0, x ∈

, x 6= p, and V

(P (x)) − V

(x) < 0, x ∈ U

, x 6= p. Next, as in i),

construct the lower semicontinuous function V : O

→ R such that V (x) =

(s(τ(x), x)), x ∈ O

, V (x) = 0, x ∈ O, V (x) > 0, x ∈ O

, x 6∈ O,

V (s(t, x)) ≤ V (s(τ, x)), 0 ≤ τ ≤ t, for every x ∈ O

⊆ O

, and V (·)

is continuous on O. Furthermore, for every x ∈ O

deﬁne an increasing

unbounded sequence {t

}

∞

n=0

such that t

= 0 and t

= τ(z(k − 1)), k =

1, 2, . . ., where z(·) satisﬁes (4.280) with z(0) = x. Th en it follows from