Haddad W.M. Nonlinear Dynamical Systems and Control: A Lyapunov-Based Approach

Подождите немного. Документ загружается.

NonlinearBook10pt November 20, 2007

ADVANCED STABILITY THEORY 295

the deﬁnition of the fu nction V (·) that V (s(t

n+1

, x)) < V (s(t

, x)), n ∈ Z

establishing that all the conditions of the Theorem 4.29 hold, and hen ce,

the periodic orbit O is asymptotically stable.

To show suﬃciency, assume that the periodic orbit O generated by

the point p ∈ D is asymptotically stable. Then it follows fr om the Theorem

4.30 that there exists a continuous, positive-deﬁnite (on D

\ O) function

V : D

→ R such that (4.261) is strictly satisﬁed. Now, for suﬃciently small

α > 0, construct a function V

: S

→ R such that V

(x) = V (x), x ∈ S

Thus , the suﬃcient conditions of T heorem 4.33 are satisﬁed for V

(·) which

implies that the point x = p is an asymptotically stable ﬁ x ed point of (4.280).

Theorem 4.34 is a restatement of the classical Poincar´e theorem.

However, in proving necessary and suﬃ cient conditions for Lyapunov

and asymptotic stability of the periodic orbit O, we constru cted explicit

Lyapunov fu nctions in the proof of Theorem 4.34. Speciﬁcally, in order to

show necessity of Poincar´e’s theorem via Lyapunov’s second method we

constructed the lower semicontinuous (respectively, continuous), positive

deﬁnite (on O

\O) Lyapunov f unction

V (x) = V

(s(τ(x), x)), x ∈ O

, (4.281)

where the existence of the lower semicontinuous (respectively, continuous),

positive deﬁ nite (on S

\ p) function V

: S

→ R is guaranteed by the

Lyapunov (respectively, asymptotic) stability of a ﬁxed point p ∈ D of

(4.280). Alternatively, in the proof of suﬃciency, Lyapunov (respectively,

asymptotic) stability of the periodic orbit O implies the existence of the

lower semicontinuous (respectively, continuous), positive deﬁnite (on D

\O)

Lyapunov function given by

V (x) = sup

t≥0

dist(s(t, x), O), x ∈ D

, (4.282)

and

V (x) =

∞

sup

t≥0

dist(s(t, s(τ, x)), O)e

−τ

dτ, x ∈ D

, (4.283)

respectively. Using the Lyapunov function V

(x) = V (x), x ∈ S

, we showed

the stability of a ﬁxed point p ∈ D of (4.280).

Theorem 4.34 presents necessary and suﬃcient conditions for Lya-

punov and asymptotic stability of a periodic orbit of the nonlinear dynamical

system (4.251) based on the stability properties of a ﬁxed point of the n-

dimensional discrete-time dynamical system (4.280) involving th e Poincar´e

map (4.278). Next, we present a classical corollary to Poincar´e’s theorem

that allows us to analyze the stability of periodic orbits by replacing the

NonlinearBook10pt November 20, 2007

296 CHAPTER 4

nth-order nonlinear dyn amical system by an (n − 1)th-order discrete-time

system. To present this result assume, without loss of generality, that

∂X(x)

∂x

6= 0, x ∈ S

, where x = [x

, . . . , x

]

and α > 0 is s uﬃciently small.

Then it follows from the implicit function theorem (see Theorem 2.18) that

= g(x

, . . . , x

n−1

), where g(·) is a continuously d iﬀerentiable function at

△

= [x

, . . . , x

n−1

]

such that [x

, g(x

)]

∈ S

. Note that in this case

P : U

→ S

in (4.280) is given by P (x)

△

= [P

(x), · ··, P

(x)]

, where

, g(x

)) = g(P

, g(x

)), . . . , P

n−1

, g(x

))). (4.284)

Hence, we can reduce the n-dimensional discrete-time system (4.280) to the

(n − 1)-dimensional discrete-time system given by

(k + 1) = P

(k)), k ∈ Z

, (4.285)

where z

∈ R

n−1

, [z

(·), g(z

(·))]

∈ S

, and

)

△

, g(x

))

n−1

, g(x

))

. (4.286)

Note that it follows from (4.284) and (4.286) that p

△

= [p

, g(p

)]

∈ S

is a ﬁxed point of (4.280) if and only if p

is a ﬁxed point of (4.285). To

present the following result deﬁne S

rα

△

= {x

∈ R

n−1

: [x

, g(x

)]

∈ S

}

and U

rα

△

= {x

∈ S

rα

: [x

, g(x

)]

∈ U

Corollary 4.8. Consider the nonlinear dynamical system (4.251) with

the Poincar´e return map deﬁned by (4.278). Assume that

∂X(x)

∂x

6= 0, x ∈ S

and the point p ∈ S

generates the periodic orbit O

△

= {x ∈ D : x =

s(t, p), 0 ≤ t ≤ T }, where s(t, p), t ≥ 0, is the periodic solution with the

period T = τ(p) such that s(τ (p), p) = p. Then the following statements

hold:

i) For p = [p

, g(p

)]

∈ S

, p

is a Lyapunov s table ﬁxed point of (4.285)

if and only if the periodic orbit O is Lyapunov stable.

ii) For p = [p

, g(p

)]

∈ S

, p

is an asymptotically stable ﬁxed point of

(4.285) if and only if the periodic orbit O is asymptotically stable.

Proof. i) To s how necessity, assume that p

∈ S

rα

is a Lyapu nov

stable ﬁxed point of (4.285). Then it follows from Theorem 4.33 that

there exists a lower semicontinuous fun ction V

: S

rα

→ R such that

(·) is continuous at p

, V

) = 0, V

) > 0, x

6= p

, x

∈ S

rα

and V

)) − V

) ≤ 0, x

∈ U

rα

. Deﬁne V : S

→ R such that

V (x) = V

), x

∈ S

rα

. To show that V (·) is continuous at p ∈ S

consider an arbitrary sequence {x

}

∞

k=1

such that x

∈ S

and x

→ p

NonlinearBook10pt November 20, 2007

ADVANCED STABILITY THEORY 297

as k → ∞. Then, x

→ p

as k → ∞ and, since V

(·) is continuous

at p

, lim

k→∞

V (x

) = lim

k→∞

) = V

) = V (p). Hence, V (·) is

continuous at p ∈ S

. Similarly, for the sequence deﬁned above V (x) =

) ≤ lim inf

k→∞

) = lim inf

k→∞

V (x

), x ∈ S

, w hich implies

that V (·) is lower semicontinuous. Next, note that V (p) = V

) = 0

and suppose, ad absurdum, that there exists x 6= p such that x ∈ S

and

V (x) = 0. Then, V

) = 0 and x

= p

, which implies that x

= g(p

) and

x = p, leading to a contradiction. Hence, V (x) > 0, x 6= p, x ∈ S

. Next,

note that

V (P (x)) −V (x) = V

(x), . . . , P

n−1

(x)) −V

)

= V

, g(x

)), . . . , P

n−1

, g(x

))) −V

)

= V

)) − V

)

≤ 0, x ∈ U

, (4.287)

and hence, by Theorem 4.33 the point p ∈ S

is a Lyapunov stable ﬁxed

point of (4.280). Finally, Lyapunov stability of the periodic orbit O follows

from Theorem 4.34.

To show suﬃciency, assume that the periodic orbit O is Lyapunov

stable. Then, it follows from Theorem 4.34 that the point p ∈ S

is a

Lyapunov stable ﬁxed point of (4.280). Hence, it follows from Theorem

4.33 that there exists a lower semicontinuous function V : S

→ R such

that V (·) is continuous at p ∈ S

, V (p) = 0, V (x) > 0, x 6= p, x ∈ S

and V (P (x)) − V (x) ≤ 0, x ∈ U

. Next, deﬁ ne V

: S

rα

→ R such that

) = V (x

, g(x

)). The proofs of continuity of V

(·) at p

∈ S

rα

and lower

semicontinuity of V

(·) follow similarly as in the proof of necessity. Next, note

that V

) = V (p

, g(p

)) = V (p) = 0 and suppose, ad absurdum, that there

exists x

6= p

such that x

∈ S

rα

and V

) = 0. Then, V (x

, g(x

)) = 0 and

x = [x

, g(x

)]

= p, which implies that x

= p

, leading to a contradiction.

Hence, V

) > 0, x

6= p

, x

∈ S

rα

. Finally, using (4.284), it follows that

)) − V

) = V (P

), g(P

))) − V (x

, g(x

))

= V (P

), P

, g(x

))) − V (x)

= V (P (x)) −V (x)

≤ 0, x

∈ U

rα

, (4.288)

and hence, by Theorem 4.33 the point p

∈ S

rα

is a Lyapunov stable ﬁxed

point of (4.285).

ii) The proof is analogous to that of i) and, hence, is omitted.

Example 4.18. Once again consider the nonlinear dynamical system

(2.220) and (2.221) given in Example 2.38 or, equ ivalently, in polar

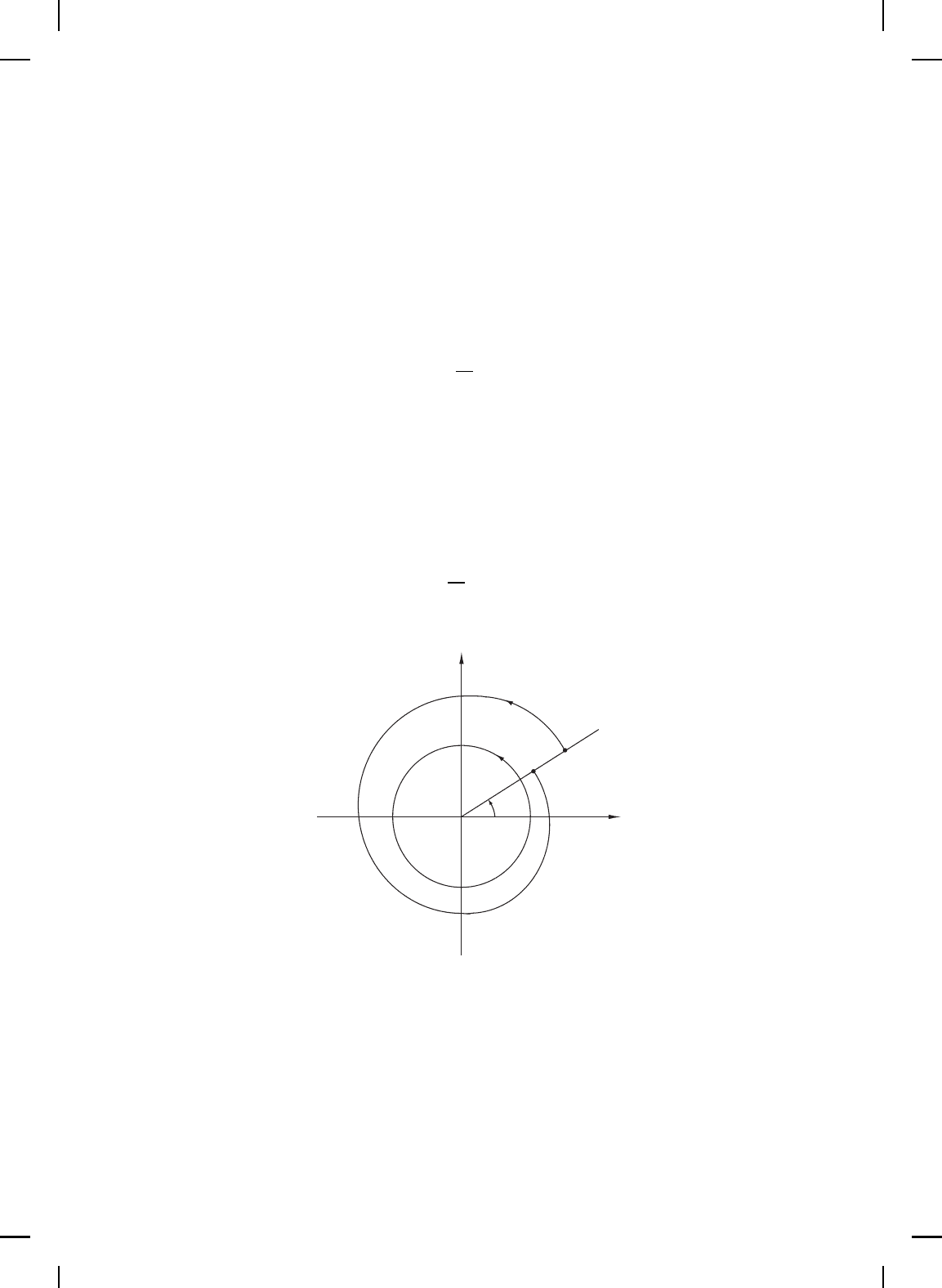
NonlinearBook10pt November 20, 2007

298 CHAPTER 4

co ordinates,

˙r(t) = r(t)



1 −r

(t)



, r(0) = r

, t ≥ 0, (4.289)

θ(t) = 1, θ(0) = θ

. (4.290)

As shown in Example 2.38, the u nit circle r = 1 is a periodic orbit for

(4.289) and (4.290). Using separation of variables the solution to (4.289)

and (4.290) is given by

r(t) =



1 +



− 1



−2t



−1/2

, (4.291)

θ(t) = θ

+ t. (4.292)

Note that if S is the ray θ = θ

through the origin of the x

-x

plane, that

is, S = {(r, θ) : θ = θ

and r > 0}, then S is perpen dicular to the periodic

orbit O and the trajectory passing through the point (r

, θ

) ∈ S ∩ O at

t = 0 intersects the ray θ = θ

again at T = 2π (see Figure 4.10). Thus, the

Poincar´e map is given by

P (r) =



1 +



− 1



−4π



−1/2

. (4.293)

P (r

)

0 1

Figure 4.10 Poincar´e map for Example 4.18.

Since (4.293) is a one-dimensional map, no reduction procedure is

necessary and Corollary 4.8 can be used directly. Since P (1) = 1, r = 1

is a ﬁxed point. Now, with z = r we examine the stability of the discrete-

NonlinearBook10pt November 20, 2007

ADVANCED STABILITY THEORY 299

time system

z(k + 1) =



1 +



(k)

− 1



−4π



−1/2

, z(0) ∈ B

(1), (4.294)

where δ > 0 is suﬃciently small. Speciﬁcally, evaluating P

′

(z) yields

′

(z) = e

−4π

−3



1 +



− 1



−4π



−3/2

, (4.295)

and hence, P

′

(1) = e

−4π

< 1. Thus, it follows from Corollary 4.8 that the

periodic orbit O = {(x

, x

) ∈ R ×R : x

= 1} is asymptotically stable.

△

Example 4.19. Consider the nonlinear d ynamical system

˙x

(t) = −x

(t) + x

(t)



1 −x

(t) −x

(t)



, x

(0) = x

, t ≥ 0, (4.296)

˙x

(t) = x

(t) + x

(t)



1 −x

(t) −x

(t)



, x

(0) = x

, (4.297)

˙x

(t) = −x

(t), x

(0) = x

. (4.298)

It can easily be shown that x(t) = [x

(t), x

(t)]

= [cos t, sin t, 0]

is a

periodic solution of (4.296)–(4.298) with period T = 2π (see Problem 2.141).

To examine the stability of this periodic solution we rewrite (4.296)–(4.298)

in terms of the cylindrical coordinates r =

+ x

, θ = tan

−1





, and

ˆz = x

˙r(t) = r(t)[1 − r

(t)], r(0) = r

, t ≥ 0, (4.299)

θ(t) = 1, θ(0) = θ

, (4.300)

ˆz(t) = −ˆz(t), ˆz(0) = ˆz

. (4.301)

Note that the solution to (4.299) and (4.300) are given by (4.298) and

(4.299), respectively, and the solution to (4.301) is given by ˆz(t) = ˆz

−t

Furth ermore, since the periodic orbit of (4.296)–(4.298) lies in the x

-x

plane we take S = {(r, θ, ˆz) : θ = θ

, r > 0, and ˆz ∈ R}. Note that S is

perpendicular to the periodic orbit and the trajectory passing through the

point (r

, θ

, ˆz

) ∈ S ∩ O at t = 0 intersects the plane again at T = 2π.

Thus , the Poincar´e map is given by

P (r, ˆz) =



1 +



− 1



−4π



−1/2

ˆze

−2π

. (4.302)

Clearly, P (1, 0) = (1, 0), and hence, [1, 0]

is a ﬁxed point. Now, with

NonlinearBook10pt November 20, 2007

300 CHAPTER 4

= r and z

= ˆz we examine the stability of the discrete-time system

(k + 1)







1 +



(k)

− 1



−4π



−1/2

(k)e

−2π





(0), z

(0)]

∈ B

([1, 0]

), (4.303)

where δ > 0 is suﬃciently small. Speciﬁcally, evaluating P

′

(z) yields

′

, z

) =





−4π

−3



1 +



− 1



−4π



−3/2

0 e

−2π





(4.304)

so that ρ(P

′

(1, 0)) = e

−2π

< 1. Hence, it follows from Corollary 4.8 that

the periodic orbit O = {(x

, x

) ∈ R

: x

+ x

= 1 and x

= 0} is

asymptotically stable. △

4.11 Stability Theory via Vector Lyapunov Functions

In this section, we introduce the notion of vector Lyapunov functions

for stability analysis of nonlinear dynamical sys tems. The use of vector

Lyapunov functions in dyn amical system theory oﬀers a very ﬂexible

framework since each component of the vector Lyapunov function can satisfy

less rigid requirements as compared to a s ingle scalar Lyapunov function.

Speciﬁcally, sin ce for many nonlinear dynamical systems constructing a

system Lyapunov function can be a diﬃcult task, weakening the hypothesis

on the Lyapunov function enlarges the class of L yapunov functions that can

be used for analyzing system stability. Moreover, in certain applications,

such as the analysis of large-scale nonlinear dynamical systems, several

Lyapunov functions arise naturally from the stability properties of each

individual subsystem. To develop the theory of vector Lyapunov functions,

we ﬁrst introduce some resu lts on vector diﬀerential inequalities and the

vector comparison principle. The following deﬁnition introdu ces the notion

of class W functions involving quasimonotone increasing functions.

Deﬁnition 4.13. A function w = [w

, . . . , w

]

: R

→ R

is of class

W if w

′

) ≤ w

′′

), i = 1, . . . , q, for all z

′

, z

′′

∈ R

such that z

′

≤ z

′′

, z

′

′′

, j = 1, . . . , q, i 6= j, w here z

denotes the ith component of z.

If w(·) ∈ W we say that w satisﬁes the Kamke condition. Note that

if w(z) = W z, w here W ∈ R

q×q

, then the function w(·) is of class W if and

only if W is essentially nonnegative, that is, all the oﬀ-diagonal entries of

the matrix function W are nonnegative. Fur thermore, note th at it follows

from Deﬁnition 4.13 that any scalar (q = 1) function w(z) is of class W.

NonlinearBook10pt November 20, 2007

ADVANCED STABILITY THEORY 301

Next, we introduce th e n otion of class W

functions involving nonde-

creasing fun ctions.

Deﬁnition 4.14. A function w = [w

, . . . , w

]

: R

→ R

is of class

if w(z

′

) ≤≤ w(z

′′

) for all z

′

, z

′′

∈ R

such that z

′

≤≤ z

′′

Note that if w(·) ∈ W

, then w(·) ∈ W. Next, we consider the

nonlinear comparison system given by

˙z(t) = w(z(t)), z(t

) = z

, t ∈ I

, (4.305)

where z(t) ∈ Q ⊆ R

, t ∈ I

, is the comparison system state vector, I

⊆

T ⊆ R

is the maximal interval of existence of a solution z(t) of (4.305), Q

is an open set, 0 ∈ Q, and w : Q → R

. We assum e that w(·) satisﬁes the

Lipschitz condition

kw(z

′

) −w(z

′′

)k ≤ Lkz

′

− z

′′

k, (4.306)

for all z

′

, z

′′

∈ B

), where δ > 0 and L > 0 is a Lipschitz constant. Hence,

it follows from Theorem 2.25 that there exists τ > 0 such that (4.305) has

a unique solution over the time interval [t

, t

+ τ ].

Theorem 4.35. Consider th e nonlinear comparison system (4.305).

Assume that the function w : Q → R

is continuous and w(·) is of class W. If

there exists a continuously diﬀerentiable vector function V = [v

, . . . , v

]

→ Q such that

V (t) << w(V (t)), t ∈ I

, (4.307)

then V (t

) << z

, z

∈ Q, implies

V (t) << z(t), t ∈ I

, (4.308)

where z(t), t ∈ I

, is the solution to (4.305).

Proof. Since V (t), t ∈ I

, is continuous it follows th at for suﬃciently

small τ > 0,

V (t) << z(t), t ∈ [t

, t

+ τ ]. (4.309)

Now, suppose, ad absurdum, that inequality (4.308) does not hold on the

entire interval I

. Then there exists

t ∈ I

such that V (t) << z(t), t ∈

t), and for at least one i ∈ {1, . . . , q},

(

t) = z

(

t) (4.310)

and

(

t) ≤ z

(

t), j 6= i, j = 1, . . . , q. (4.311)

NonlinearBook10pt November 20, 2007

302 CHAPTER 4

Since w(·) ∈ W, it follows from (4.307), (4.310), and (4.311) that

˙v

(

t) < w

(V (

t)) ≤ w

(z(

t)) = ˙z

(

t), (4.312)

which, along with (4.310), implies that for suﬃciently s mall ˆτ > 0, v

(t) >

(t), t ∈ [

t − ˆτ,

t). This contradicts the fact that V (t) << z(t), t ∈ [t

t),

and establishes (4.308).

Next, we present a stronger version of Theorem 4.35 where the strict

inequalities are replaced by soft inequalities.

Theorem 4.36. Consider the nonlinear comparison system (4.305).

Assume that the fun ction w : Q → R

is continuous and w(·) is of class

W. Let z(t), t ∈ I

, be the solution to (4.305) and [t

, t

+ τ] ⊆ I

be a

compact interval. If there exists a continuously diﬀerentiable vector function

V : [t

, t

+ τ ] → Q such that

V (t) ≤≤ w(V (t)), t ∈ [t

, t

+ τ ], (4.313)

then V (t

) ≤≤ z

, z

∈ Q, implies

V (t) ≤≤ z(t), t ∈ [t

, t

+ τ ]. (4.314)

Proof. Consider the family of comparison systems given by

˙z(t) = w(z(t)) +

e, z(t

) = z

e, (4.315)

where ε > 0, n ∈ Z

, and t ∈ I

, and let the solution to (4.315) be

denoted by s

(n)

(t, z

e), t ∈ I

. Now, it follows f rom Theorem 3

of [98, p. 17] that s

(n)

(t, z

e), t ∈ [t

, t

+τ], is deﬁned for all suﬃciently

large n. Moreover, it follows from Theorem 4.35 that

V (t) << s

(n)

(t, z

e) << s

(m)

(t, z

e), n > m, t ∈ [t

, t

+ τ ],

(4.316)

for all suﬃciently large m ∈ Z

. Since the functions s

(n)

(t, z

e), t ∈

, t

+ τ], n ∈ Z

, are continuous in t, decreasing in n, and bounded from

below, it follows that the sequen ce of functions s

(n)

(·, z

e) converges

uniformly on the compact interval [t

, t

+τ ] as n → ∞, that is, there exists

a continuous function ˆz : [t

, t

+ τ ] → Q such that

(n)

(t, z

e) → ˆz(t), n → ∞, (4.317)

uniformly on [t

, t

+ τ ]. Hence, it follows from (4.316) and (4.317) that

V (t) ≤≤ ˆz(t), t ∈ [t

, t

+ τ]. (4.318)

NonlinearBook10pt November 20, 2007

ADVANCED STABILITY THEORY 303

Next, note that it follows from (4.315) that

(n)

(t, z

e) = z

e +

w(s

(n)

(σ, z

e))dσ,

t ∈ [t

, t

+ τ ], (4.319)

which implies that ˆz(t

) = z

and, since w(·) is continuous, w(s

(n)

(t, z

e)) → w(ˆz(t)) as n → ∞ uniform ly on [t

, t

+ τ]. Hence, taking the limit

as n → ∞ on both sides of (4.319) yields

ˆz(t) = z

w(ˆz(σ))dσ, t ∈ [t

, t

+ τ ], (4.320)

which implies that ˆz(t) is the s olution to (4.305) on the interval [t

, t

τ]. Hence, by uniqueness of solutions of (4.305) we obtain that ˆz(t) =

z(t), [t

, t

+ τ ]. This, along with (4.318), proves the result.

Next, consider the nonlinear dynamical system given by

˙x(t) = f(x(t)), x(t

) = x

, t ∈ I

, (4.321)

where x(t) ∈ D ⊆ R

, t ∈ I

, is the system state vector, I

is th e maximal

interval of existence of a s olution x(t) of (4.321), D is an open set, 0 ∈

D, and f (·) is Lipschitz continuous on D. The following result is a d irect

consequence of Theorem 4.36.

Corollary 4.9. C onsider the nonlinear dynamical system (4.321).

Assume there exists a continuously diﬀerentiable vector function V : D →

Q ⊆ R

such that

′

(x)f(x) ≤ ≤ w(V (x)), x ∈ D, (4.322)

where w : Q → R

is a continuous function, w(·) ∈ W, and

˙z(t) = w(z(t)), z(t

) = z

, t ∈ I

, (4.323)

has a unique solution z(t), t ∈ I

. If [t

, t

+ τ ] ⊆ I

∩ I

is a compact

interval, then V (x

) ≤≤ z

, z

∈ Q, implies V (x(t)) ≤≤ z(t), t ∈ [t

, t

+τ ].

Proof. For every x

∈ D, the solution x(t), t ∈ I

, to (4.321) is a well

deﬁned function of time. Hence, deﬁne η(t) , V (x(t)), t ∈ I

, and note

that (4.322) implies

˙η(t) ≤≤ w(η(t)), t ∈ I

. (4.324)

Moreover, if [t

, t

+τ] ⊆ I

∩I

is a compact interval, then it follows from

Theorem 4.36, with V (x

) = η(t

) ≤≤ z

, that V (x(t)) = η(t) ≤≤ z(t), t ∈

, t

+ τ ], which establishes the result.

If in (4.321) f : R

→ R

is globally Lip s chitz continuous, then (4.321)

NonlinearBook10pt November 20, 2007

304 CHAPTER 4

has a unique solution x(t) for all t ≥ t

. A more restrictive s uﬃcient

condition for global existence and uniqueness of solutions to (4.321) is

continuous diﬀerentiability of f : R

→ R

and uniform boundedness of

′

(x) on R

. Note that if the solutions to (4.321) and (4.323) are globally

deﬁned for all x

∈ D and z

∈ Q, then the result of Corollary 4.9 holds

for every arbitrarily large but compact interval [t

, t

+ τ ] ⊂ R

. For the

remainder of this section we assume that the s olutions to th e systems (4.321)

and (4.323) are deﬁ ned for all t ≥ t

Consider the nonlinear comparison system given by

˙z(t) = w(z(t)), z(t

) = z

, t ≥ t

, (4.325)

and the nonlinear d ynamical system given by

˙x(t) = f (x(t)), x(t

) = x

, t ≥ t

, (4.326)

where z

∈ Q ⊆ R

, x

∈ D ⊆ R

, w : Q → R

is continuous, w(·) ∈ W,

w(0) = 0, f : D → R

is Lipschitz continuous on D, and f(0) = 0. Note

that since w(·) ∈ W and w(0) = 0, then for every z ∈ Q ∩ R

such that

= 0 it follows that w

(z) ≥ 0, i = 1, . . . , q, which imp lies that for every

∈ Q ∩ R

the solution z(t), t ≥ t

, remains in R

(see Problem 3.61).

Theorem 4.37. Consider the nonlinear dynamical system (4.326).

Assume that there exist a continuously diﬀerentiable vector function V :

D → Q ∩ R

and a positive vector p ∈ R

such that V (0) = 0, the scalar

function v : D → R

deﬁned by v(x) , p

V (x), x ∈ D, is such that

v(x) > 0, x 6= 0, and

′

(x)f(x) ≤ ≤ w(V (x)), x ∈ D, (4.327)

where w : Q → R

is continuous, w(·) ∈ W, and w(0) = 0. Then the

following statements hold:

i) If the zero solution z(t) ≡ 0 to (4.325) is Lyapunov stable, then the

zero solution x(t) ≡ 0 to (4.326) is Lyapunov stable.

ii) I f the zero solution z(t) ≡ 0 to (4.325) is asymptotically stable, then

the zero solution x(t) ≡ 0 to (4.326) is asymptotically s table.

iii) If D = R

, Q = R

, v : R

→ R

is radially unbounded, and the zero

solution z(t) ≡ 0 to (4.325) is globally asymptotically stable, then the

zero solution x(t) ≡ 0 to (4.326) is globally asymptotically stable.

iv) If there exist constants ν ≥ 1, α > 0, and β > 0 such that v : D → R

satisﬁes

αkxk

≤ v(x) ≤ βkxk

, x ∈ D, (4.328)