Gupta D. (Ed.). Diffusion Processes in Advanced Technological Materials
Подождите немного. Документ загружается.


(b) for a free and an impenetrable surface, respectively. As the dislocations
advance in the film by “channeling,” they create additional dislocation
segments along the bottom and the top surface if it is impenetrable. This
mechanism has been observed for the motion of dislocation in large-
grained polycrystalline Al films on amorphous substrates
[9]
and in epitax-
ial Al films on Si
[41]
or Al
2
O
3
substrates.
[42]
For this last example, Fig. 8.13
shows a dislocation, which has channeled over a distance of several
micrometers. It appears that there is a repulsive force from the interface
on the dislocation as it stands off by as much as 100 nm. The contrast
close to the interface indicates the presence of other dislocations, which
may be related to the epitaxial misfit.
In contrast, it was observed that in polycrystalline films with grain
size of the order of the film thickness, dislocations did not channel.
Kobrinsky and Thompson
[32]
describe the dislocation motion below
150°C in thin Ag films (200 nm in thickness) as jerky. As observed
during in situ transmission electron microscopy (TEM), dislocations
are pinned by obstacles and do not move most of the time, until a sud-
den jump of a dislocation segment between two pinning points is
observed. The typical pinning point and jump distances were both
found to be between 50 and 100 nm, which are significantly smaller
than the film thickness or grain size. These observations are confirmed
by in situ TEM, both in cross section as well as in plan view, on poly-
crystalline Cu films that were deposited onto amorphous SiN
x
layers
on Si substrates.
[42, 43]
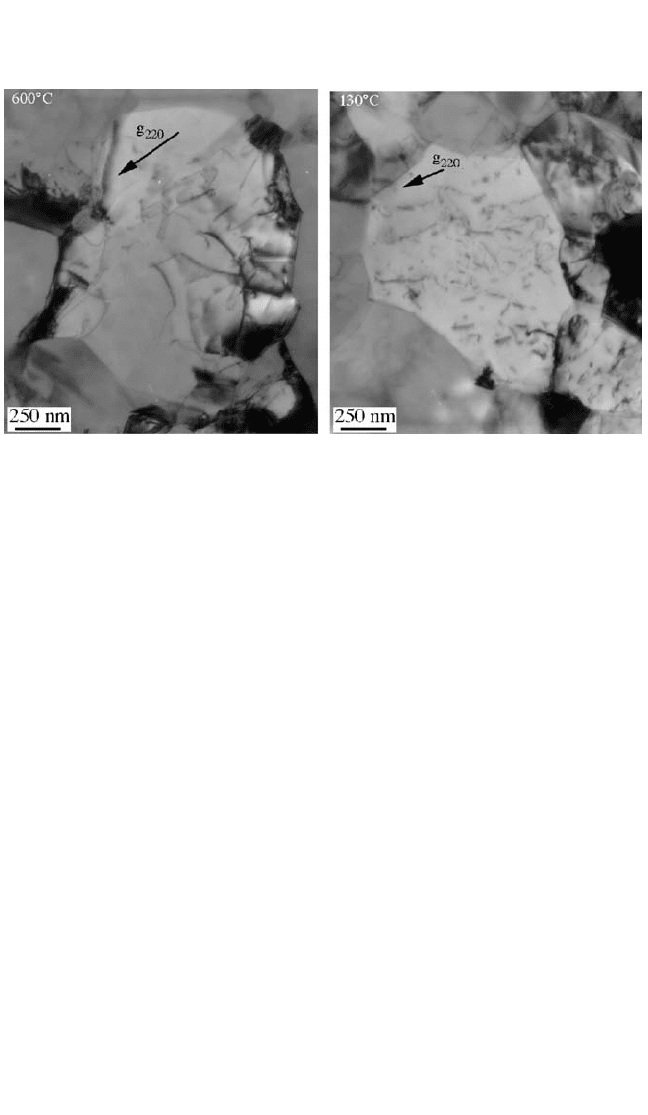
Figure 8.14 shows the typical dislocation distri-
bution after cooling from 600 to 130°C in such a film. At tempera-
382 DIFFUSION PROCESSES IN ADVANCED TECHNOLOGICAL MATERIALS
Figure 8.13 Dislocation in a 350-nm-thick Al film that was grown epitaxially on a
(0001)-oriented Al
2
O
3
substrate. Glide of a dislocation on the Al plane, which is
inclined ∼70 degrees to the (111)Al G (0001)Al
2
O
3
interface, created a dislocation
segment nearly parallel to the interface. Contrast near the film/substrate interface
indicates the presence of other, possibly misfit, dislocations. The cross-sectional
TEM image is from Dehm et al.
[42]
with permission.
Ch_08.qxd 11/29/04 6:45 PM Page 382
STRESSES IN THIN FILMS AND THEIR RELAXATION, KRAFT, GAO 383
tures below 220°C, short segments of tangled dislocations and a
jerky dislocation motion were observed. It was also pointed out that
no interfacial dislocation segments were found, which would be
expected for the dislocation motion described by Fig. 8.12.
Furthermore, cross-sectional in situ TEM revealed that dislocations
are attracted rather than repelled by the Cu/SiN
x
interface and, again,
no evidence for interfacial dislocation segments was found.
[43]
In
contrast, Shen et al.
[34]
and Weihnacht and Brückner
[44]
observed
interfacial dislocations and dislocation pileup in plan-view and
cross-sectional TEM, respectively.
Nix
[1]
and Freund
[45]
have derived the following formalism for the
motion of a single dislocation in a thin film, as shown in Fig. 8.12. As the
dislocation channels through the film, an interface dislocation segment is
created. As a result, the critical resolved shear stress t
y
to move a disloca-
tion in a thin film depends on its thickness h and is given by:
t
y,Nix
2p(
b
1
G
eff
n)
sin
h
j
,(11)
Figure 8.14 Dislocations in Cu grains at (a) 600°C and (b) 130°C. No interfacial
dislocations deposited by advancing threading dislocations are discernable in the
images. At elevated temperatures (a), dislocations appear to be longer and more
mobile than at lower temperatures (b), where dislocation motion became jerky and
dislocation tangles formed. Plan-view TEM images are from Dehm et al.,
[42]
with
permission.
Ch_08.qxd 11/29/04 6:45 PM Page 383

where
G
eff
ln
x
b
s
h
; (12)
j is the angle between the glide plane normal and the film normal; bis the
magnitude of the Burgers vector; n is Poisson’s ratio; G and G
s
are the
shear moduli of the film and the substrate, respectively; and x
s
is a numer-
ical constant close to unity that defines the cutoff radius of the stress field
of the dislocation at the film/substrate interface. Extending this model to
polycrystalline thin films, Thompson
[46]
suggested that additional disloca-
tion segments must be created at the grain boundaries. This reasoning
results in the following critical shear stress:
t
y,Th
sin
h
j
, (13)
with
W
d
4p(
G
1
b
2
n)
ln
, (14)
where d is the grain size and W
d
is the line energy of the dislocation seg-
ments along the grain boundaries and the film/substrate interface where,
for the sake of simplicity, Thompson assumed that the effective modulus
equals the film modulus (G G
eff
). As can be seen from Eqs. (11) and
(13), these models predict nearly a 1/h and/or a 1/d dependence of the
yield strength. Asimilar result has been also obtained by Chaudhari.
[47]
An experimental validation of these models has been given by
Venkatraman and Bravman
[9]
for coarse-grained Al films or by Dehm
et al.
[48]
for epitaxial thin Al films on Al
2
O
3
substrates. However, for most
polycrystalline fine-grained films, the model tends to underestimate the
yield strength.
[13, 22]
Kobrinsky and Thompson
[32]
pointed out that it is not
adequate to use the simple picture shown in Fig. 8.12 for dislocation
motion in thin films to predict their strength. This is because a much more
complex dislocation behavior is observed in TEM, including the jerky
motion of dislocations at low temperatures and the absence of interface
dislocations. Also, time-dependent stress relaxation in thin films is not
addressed by this model. Therefore, Kobrinsky and Thompson suggest
that dislocation-mediated plasticity in thin metal films is significantly
d
b
2
d
W
d
b
GG
s
G G
s
384 DIFFUSION PROCESSES IN ADVANCED TECHNOLOGICAL MATERIALS
Ch_08.qxd 11/29/04 6:45 PM Page 384
STRESSES IN THIN FILMS AND THEIR RELAXATION, KRAFT, GAO 385
affected by thermal activation of the dislocation glide. Note that this
mechanism was previously discussed by Flinn et al.
[5]
and Volkert et al.
[10]
to control the stress-temperature behavior of Al thin films.
The thermally activated glide of dislocations implies that the applied
shear stress is not large enough to drive a dislocation through an array of
obstacles, such as forest dislocations or particles. As a result, dislocations are
pinned at these obstacles. However, thermal activation may provide the addi-
tional energy to help a dislocation segment to overcome the obstacle. This
results in the observed jerky motion as a dislocation moves step by step from
obstacle to obstacle. Aconstitutive law for the thermally activated glide can
be given if a certain obstacle “shape” is assumed. For rectangular obstacles,
the plastic deformation rate e
is given by Frost and Ashby [49, p. 8]:
e
e
o
exp
1
s
t
s
^
, (15)
where e
o
is a characteristic constant, ∆F is the activation energy at zero
stress, t
^
is the critical shear stress without thermal activation, and s is the
Schmid factor.
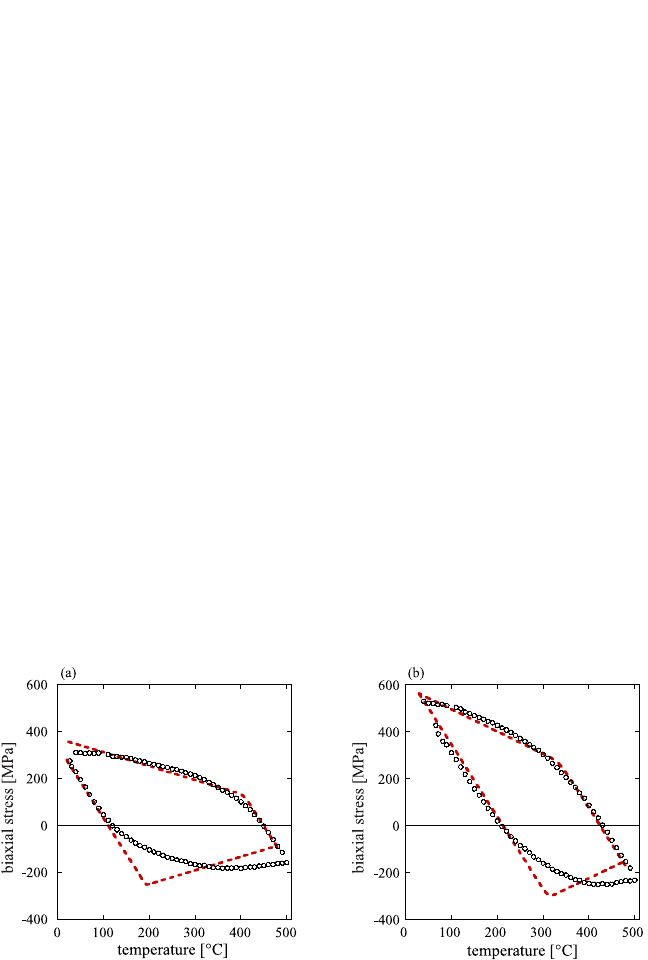
Figure 8.15 compares this approach and experimental data for self-
passivated 0.5 and 1.0 µm thick Cu 1 at.% Al films. The starting points on
F
kT
Figure 8.15 Stress evolution as a function of temperature for Cu films with a cap
layer and a thickness of (a) 1.0 mm and (b) 0.5 µm.The film stress was measured
by the wafer curvature technique.
[29]
The dashed lines represent modeled curves
for thermally activated dislocation glide. Parameters used were for bulk Cu:
[49]
e
o
1 10
6
s
1
, ∆F 3.5 10
19
J.The Schmid s 0.27 is for (111)-oriented grains.
t
^
was adjusted to 150 and 235 MPa for the 1.0- and 0.5-µm-thick films, respectively.
Ch_08.qxd 11/29/04 6:45 PM Page 385
heating were adjusted to the experimental value. It can be seen that a reason-
able agreement is obtained, although the compressive plateau is not well rep-
resented. The agreement for the two film thicknesses was obtained by adjust-
ing t
^
to 150 and 235 MPa, respectively. Using Orowan’s classical result that
the critical shear stress depends on the pinning point distance L as t
^
GbL,
the corresponding pinning point distances are 80 and 50 nm, respectively.
These values are indeed much smaller than the film thickness and of the same
order of magnitude as the ones determined by in situ TEM on Ag films.
[15, 43]
However, the approach presented here does not take into account that the pin-
ning point distance changes during heating and cooling (see Fig. 8.14) as a
result of strain hardening and possibly recovery processes.
Strong kinematic strain hardening is a competing approach to model
the stress-temperature curves for explaining some of the observed
effects. Shen et al.
[34]
suggested that the increase in flow stress on cool-
ing is related to the buildup of a back stress s
b
, which lowers the yield
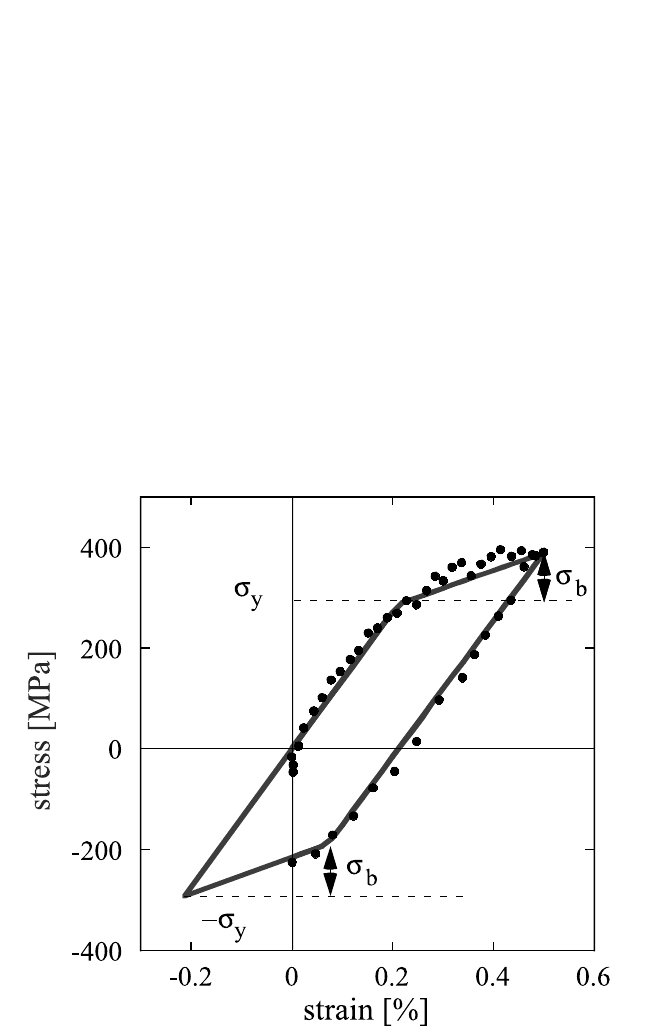
strength on reverse loading. This behavior is represented in Fig. 8.16:
386 DIFFUSION PROCESSES IN ADVANCED TECHNOLOGICAL MATERIALS
Figure 8.16 Stress-strain curve given by the kinematic strain-hardening model in
Shen et al.
[34]
under cyclic loading, compared to the experimental data from Fig.8.2.
Ch_08.qxd 11/29/04 6:45 PM Page 386

STRESSES IN THIN FILMS AND THEIR RELAXATION, KRAFT, GAO 387
After the stress reaches s
y
on loading, plastic deformation occurs with a
linear increase in flow stress. Due to this increase, a back stress s
b
builds up. On reverse loading, the yield strength in compression is
lowered by this back stress and the film yields at s
reverse
s
y
s
b
.
Figure 8.16 also shows that this predicted behavior is in agreement with
the cyclic stress-strain behavior of the Cu films on polyimide substrates.
Shen et al. have shown in their original work that their model can be
applied fairly well to model thermal stress cycles of Cu films when a
temperature-dependent yield strength is assumed. The incremental
increase in stress, that is, the hardening rate, in the elastic-plastic regime
is given by:
∂s
,
(16)
where M is the biaxial modulus of the film, e
*
is the hardening parame-
ter, and s
y
(T) is the temperature-dependent yield strength. The yield
strength was assumed to decrease linearly with temperature, that is,
s
y
(T) s
o
(1 TT
*
), where s
o
is the yield strength at T 0 K and T
*
is the temperature at which the yield strength becomes zero. Hence, e
*
,
s
o
, and T
*
can be used to fit the model empirically to experimental data.
Nix and Leung
[50]
have adapted this approach and tried to reduce the
empirical fit parameters. They suggested that the yield strength is
related to the dislocation motion in the film, as given by Eq. (11).
Therefore, its temperature dependence is related to the temperature
dependence of the shear modulus, which can be assumed to be G
G
o
(1 c
*
(T 300)T
m
), where G
o
is the shear modulus at room tem-
perature, c
*
is a constant close to 0.5 for most FCC metals, and T
m
is the
melting temperature.
Figure 8.17 shows a quantitative comparison of this approach to
the data from Fig. 8.15. Again, a reasonable agreement between
experiment and model can be seen. In particular, the plateau in com-
pression is well reproduced. Note that the hardening rate, which is
adjusted to fit the experimental data, is of the order of the shear
modulus of Cu, which is about two orders of magnitude larger than
the hardening rate in bulk Cu. Furthermore, this approach does not
allow us to account for any time-dependent deformation; therefore, it
is not possible to account for strain rate effects or stress relaxation.
More recently, Kraft et al.
[51]
suggested that both thermally activated
dislocation glide and strain hardening be included by modifying
a∂T
M
1
s
e
y
(
*
T)
Ch_08.qxd 11/29/04 6:45 PM Page 387

Eq. (15) as:
e
e
o
exp
1
s(s
t
^
s
b
)
, (17)
where s
b
is the back stress acting on dislocations in the active slip system,
which can be, for example, described to depend linearly on the plastic
strain e
pl
: s
b
t
s
^
e
e
p
*
l
, as suggested by Shen et al. [see Eq. (16)]. The influence
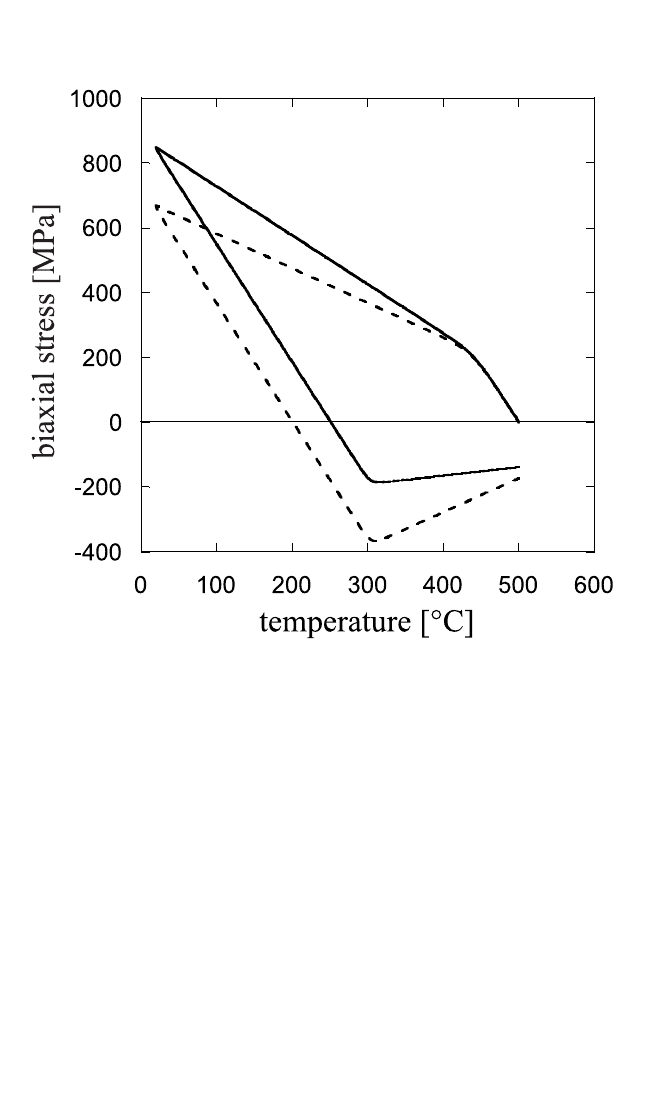
of the back stress is also illustrated in Fig. 8.18, where the behavior lead-
ing to the two stress-temperature curves is identical except for the pres-
ence (solid curve) or absence (dashed line) of the back stress. Similar to
Fig. 8.17, the effect of the back stress leads to the asymmetry in the mag-
nitude of the stresses on heating and cooling, and the high stresses are
obtained by adjusting L to 50 nm for t
^
GbL. (Compare to Fig. 8.15.)
However, the approach presented here does not take into account that the
pinning point distance changes during heating and cooling (see Fig. 8.14)
as a result of strain hardening or recovery processes.
Baker et al.
[52]
pointed out that channeling of a single dislocation, as
shown in Fig. 8.12, is completely reversible. As a result, a reduction of an
F
kT
388 DIFFUSION PROCESSES IN ADVANCED TECHNOLOGICAL MATERIALS
Figure 8.17 Experimental data from Fig. 8.15 compared to the kinematic strain-
hardening model.
[34]
The solid line represents the model using the following param-
eters: G 45 GPa, e
*
0.01, M 220 GPa. (This value was adapted to fit the
thermoelastic region.) The dashed lines indicate the yield strength as a function of
temperature.
Ch_08.qxd 11/29/04 6:45 PM Page 388
STRESSES IN THIN FILMS AND THEIR RELAXATION, KRAFT, GAO 389
applied stress below the critical stress, given by Eq. (11), should lead to
spontaneous removal of the dislocation. This phenomenon leads to a plas-
tic deformation in the reverse direction to the applied stress. Such a behav-
ior has been observed in a variety of face-centered-cubic metal films,
which were contaminated by oxygen, with the role of the oxygen not yet
understood. This effect should also influence dislocation interaction
mechanisms, which may lead to the strong (kinematic) hardening effects
in thin films. Figure 8.19 shows three scenarios that lead to hardening
behavior comparable to the experimental observations: (a) A channeling
dislocation has to overcome interfacial dislocations.
[53]
(b) The interfacial
dislocation of a channeling dislocation is deposited in an existing array of
parallel interface dislocations.
[44]
(c) The nucleation of dislocation occurs
at a Frank-Read source located in the interior of a grain. The repeated
Figure 8.18 Stress vs.temperature change for a film on a substrate, illustrating the
difference between response according to the standard plastic rate equation for
thermally activated dislocation glide [Eq. (15), dashed line] and a rate equation
modified by inclusion of a back stress, depending on plastic strain [Eq. (17), solid
line].The parameters used were the same as in Fig. 8.15 and e
*
0.005.
Ch_08.qxd 11/29/04 6:45 PM Page 389

emission of dislocation loops leads to a back-stress onto the dislocation
source,
[54, 55]
making the nucleation event more difficult from time to time.
So far, the models presented, which are intended to describe the
strength and hardening behavior of thin metal films, are based on the con-
cept of misfit dislocations; they imply that the misfit dislocation at the
interface to the amorphous substrate still supplies a stress field.
390 DIFFUSION PROCESSES IN ADVANCED TECHNOLOGICAL MATERIALS
Figure 8.19 Schematic representation of possible dislocation arrangements lead-
ing to strain hardening in a thin film on a substrate.
Ch_08.qxd 11/29/04 6:45 PM Page 390
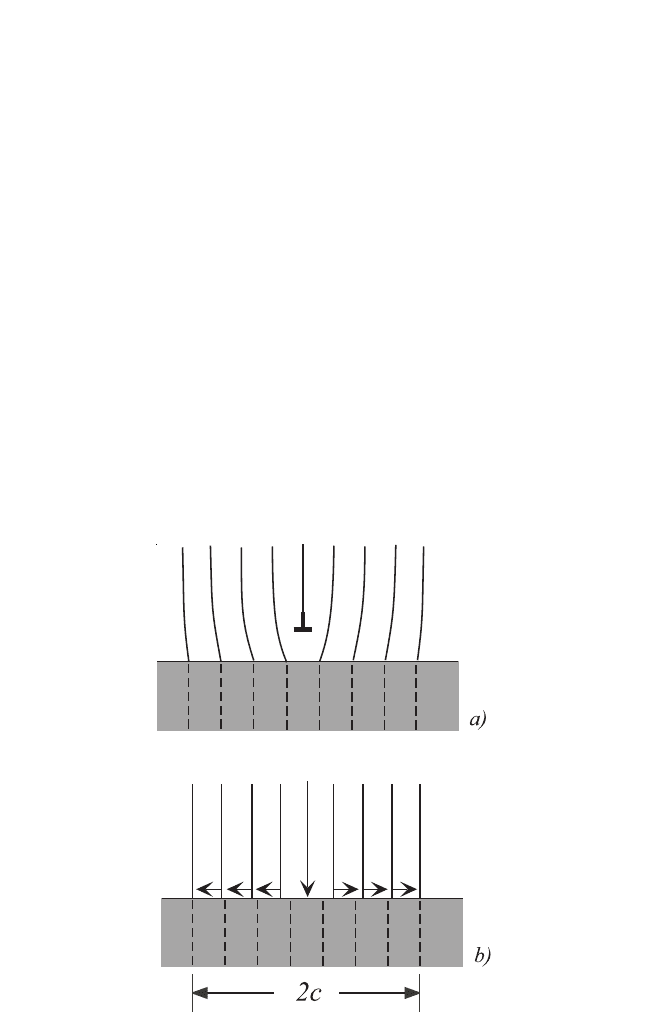
STRESSES IN THIN FILMS AND THEIR RELAXATION, KRAFT, GAO 391
Dislocation core structure is known to play an important role in the
strength of solids. The classical dislocation core models are based on a
line defect in a crystalline structure. Such models do not apply in the case
of amorphous solids. Since, in many cases, misfit dislocations are located
at an interface between a crystalline film and an amorphous substrate (or
an adhesive or functional layer between film and substrate), a fundamen-
tal question arises: What is the equilibrium core structure of dislocations
at an interface between crystalline and amorphous materials? At a crystalline-
amorphous interface, as in the case of Al or Cu films deposited on an
aSiO
x
or aSiN
x
substrate, the core of a misfit dislocation may spread along
the interface, as illustrated in Fig. 8.20. The substrate has no simple crys-
tallographic relationship to the film and hence may be thought of as a
continuum. Dashed lines have been drawn on the substrate to mark the
original positions of the atomic planes in the film. Figure 8.20 depicts an
edge dislocation with Burgers vector b parallel to the interface, climbing
toward the substrate under an applied load and then spreading its core
along the interface. The dispersed dislocation core may be modeled as an
Figure 8.20 Schematic of dislocation core spreading at an incoherent interface
between a crystalline and an amorphous solid. (a) The dislocation climbs down
toward the substrate but cannot penetrate it.(b) If it is possible for sliding to occur
at the interface, the dislocation core may spread into the interface to a width 2c.
Ch_08.qxd 11/29/04 6:45 PM Page 391
