Gupta D. (Ed.). Diffusion Processes in Advanced Technological Materials

Подождите немного. Документ загружается.

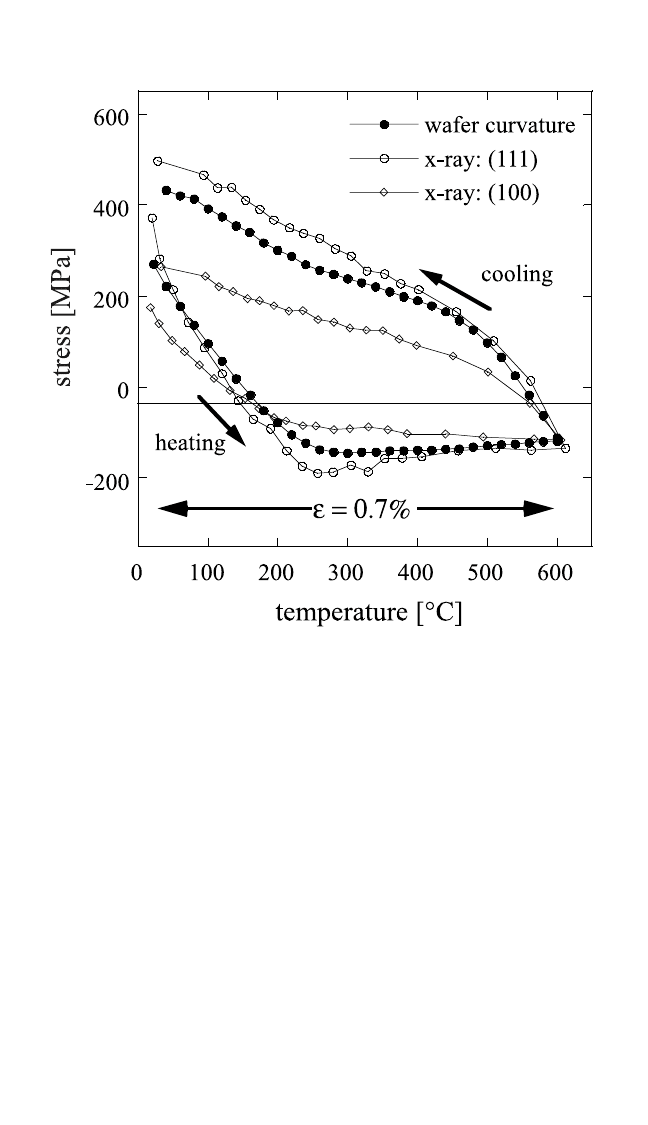
film (b) on Si substrates. At room temperature, the metal film (500-nm-thick

Cu film) is in a biaxial tensile stress state. On heating, the film tends to

expand more than the substrate and the tensile stress is reduced. At roughly

150°C, the stress equals zero, and on further heating, the film stress becomes

compressive. Up to a temperature of about 250°C, the film is deformed elas-

tically. The slope of the curve is given by ∆aE

(1  n

), which is obtained

by combining Eqs. (1) and (2). Above 250°C, the film is deformed plastically

and the compressive stress does not increase further. On cooling from the

maximum temperature of 500°C, the film contracts more than the substrate

and, as a result, the film stress becomes tensile. Again, the film is first

deformed elastically and then plastically at temperatures below 400°C. The

general trends of the described behavior are typical for many metal films (for

example, Al,

[10]

Cu,

[14]

or Ag

[15]

) because metals usually have a much higher

thermal expansion coefficient compared to substrate materials such as Si or

glass. In contrast, glass films on Si show a different behavior because the rela-

tion of the thermal expansion coefficients is reversed. Figure 8.4(b) shows the

cooling curves of two different glass films on a Si substrate. At high temper-

ature, the films cannot support any stress because the glass transition tem-

perature is exceeded and the film flows viscously. Reaching the glass transi-

tion temperature, the films are deformed elastically and stresses are produced.

Here, the films tend to contract less than the substrate and compressive

stresses arise. Note that the stress temperature curve is not linear because the

thermal expansion coefficient and Young’s modulus are not constant in the

wide range of temperatures investigated. This example shows nicely that the

measurement of film stresses is a powerful tool to study film properties. For

example, from the curves in Fig. 8.4(b), the glass transition temperature for

the two CVD-SiO

films with different dopants can be determined.

The elastic or reversible portions of the thermal cycling data can be used

to estimate the product ∆aE

(1  n

). If, for instance, two different substrates

with known but different thermal expansion coefficients are used, the values

of a

and E

(1  n

) can be determined independently for the film.

[16]

The interpretation of the stress temperature behavior to obtain infor-

mation about plasticity is not straightforward. Because the temperature

and strain are changed simultaneously, the measured stress is a complicated

function of film strength, time- and temperature-dependent creep processes,

and possibly strain hardening, voiding, or cracking events. Nevertheless,

useful information has been gained from thermal cycling experiments by

simply approximating the measured stress as the film strength at a given

temperature.

[9]

Another common experiment is to interrupt the tempera-

ture cycle at a certain temperature and to observe the stress relaxation.

[10, 11]

In this situation, the total film strain is held constant but elastic strain is

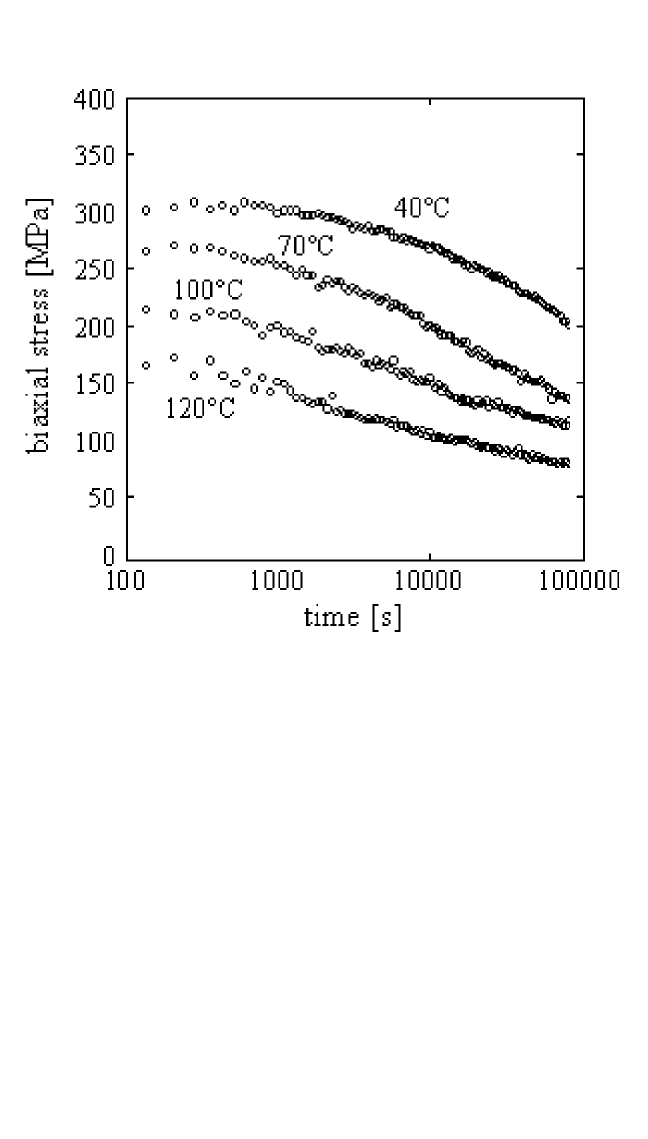
changed into plastic strain corresponding to a stress relaxation. Figure 8.5

illustrates such an experiment, showing the stress relaxation at three dif-

372 DIFFUSION PROCESSES IN ADVANCED TECHNOLOGICAL MATERIALS

Ch_08.qxd 11/29/04 6:45 PM Page 372

STRESSES IN THIN FILMS AND THEIR RELAXATION, KRAFT, GAO 373

ferent temperatures for the same film/substrate specimen after cooling

from a maximum temperature of 500°C. It can be seen that a strong initial

stress drop is observed, followed by a much slower further decrease in

stress. Mechanisms for plastic deformation and stress relaxation in metal

thin films are discussed in Sec. 8.3.

8.2.2 X-Ray Diffraction

The most common x-ray technique to determine stresses in thin films

is the so-called sin

ψ method.

[17–19]

This method is based on the measure-

ment of lattice spacings with a resolution better than 10

4

Å. This is illus-

trated in Figure 8.6, which shows a thin crystalline film stressed in tension

[Fig. 8.6(a)]. The spacing of lattice planes that are perpendicular to the

film plane is increased, due to this tension, while the spacing of planes

parallel to the film is decreased, due to Poisson’s contraction. For an equi-

Figure 8.5 Stress relaxation in a 0.6-µm-thick Cu film on a Si substrate at various

temperatures as measured by the wafer curvature technique.Data from Keller et al.

[11]

Ch_08.qxd 11/29/04 6:45 PM Page 373

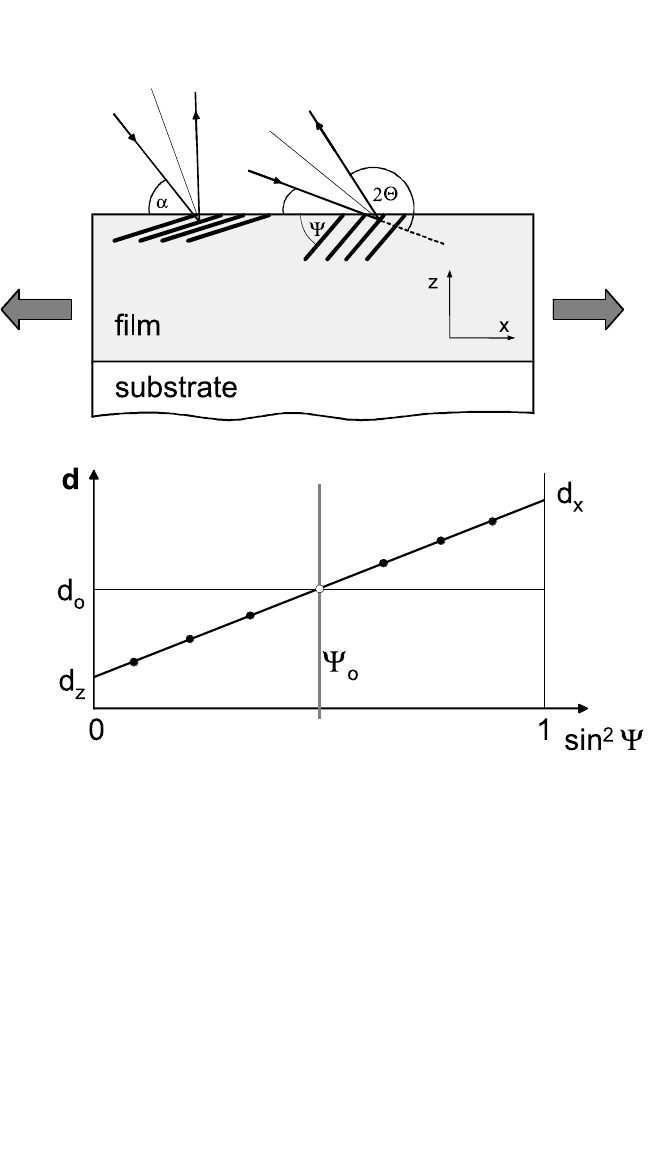
biaxial stress state, which is often present in thin films, the lattice spacing

depends linearly on sin

ψ [Fig. 8.6(b)], where ψ is the angle between

the normals of the measured lattice planes and the film surface.

Comparing the strained lattice spacings d

and d

for ψ  1 and ψ  0,

respectively, to the unstrained lattice spacing d

allows us to determine the

strains e

 e

and e

in and out of the plane of the film:

 (8a)

 . (8b)

 d



 d



374 DIFFUSION PROCESSES IN ADVANCED TECHNOLOGICAL MATERIALS

Figure 8.6 Schematic representation of the sin

ψ method for a textured thin film.

Ch_08.qxd 11/29/04 6:45 PM Page 374

STRESSES IN THIN FILMS AND THEIR RELAXATION, KRAFT, GAO 375

Furthermore, it is possible to calculate the stress state of the film using the

elastic constants of the film material. This method works particularly well

for single-crystalline or textured films with an orientation that results in an

isotropic biaxial modulus of the film. This is the case for cubic materials

with (111) and (100) planes parallel to the surface. For the latter, the

stresses are given by:

 C

 C

(9a)

 C

 C

(9b)

 C

 C

. (9c)

Note that for a (100)-oriented crystal, the Cartesian coordinate systems of the

crystal and the sample have the same orientation. This is no longer the case

for a (111)-oriented crystal or texture. Therefore, the stiffness coefficients

need to be transformed from the crystal to the sample coordinate system.

Then the stress components in the sample coordinate system are calculated

to be:

 C

 C

, (10a)

 C

 C

, (10b)

 C

 C

, (10c)

where C

,C

, and C

are the transformed stiffness coefficients.

[19]

It is obvious from Eq. (8) that the accuracy of the measurement

depends very strongly on the value used for the unstrained-lattice spacing d

Since this value depends sensitively on temperature and material impurities,

it is advantageous to determine d

for each stress measurement. This

leads also to a reduction of the influence of systematic errors in the

experimental setup related to the alignment and calibration of the

goniometer and detector. For a thin film with a strong texture, it is rea-

sonable to assume that the out-of-plane stress component s

equals zero.

Assuming an equi-biaxial stress state, it can be shown that the unstrained

lattice spacing is given for sin

 2C

(C

 2C

), where the

appropriate stiffness coefficients for the sample coordinate system are

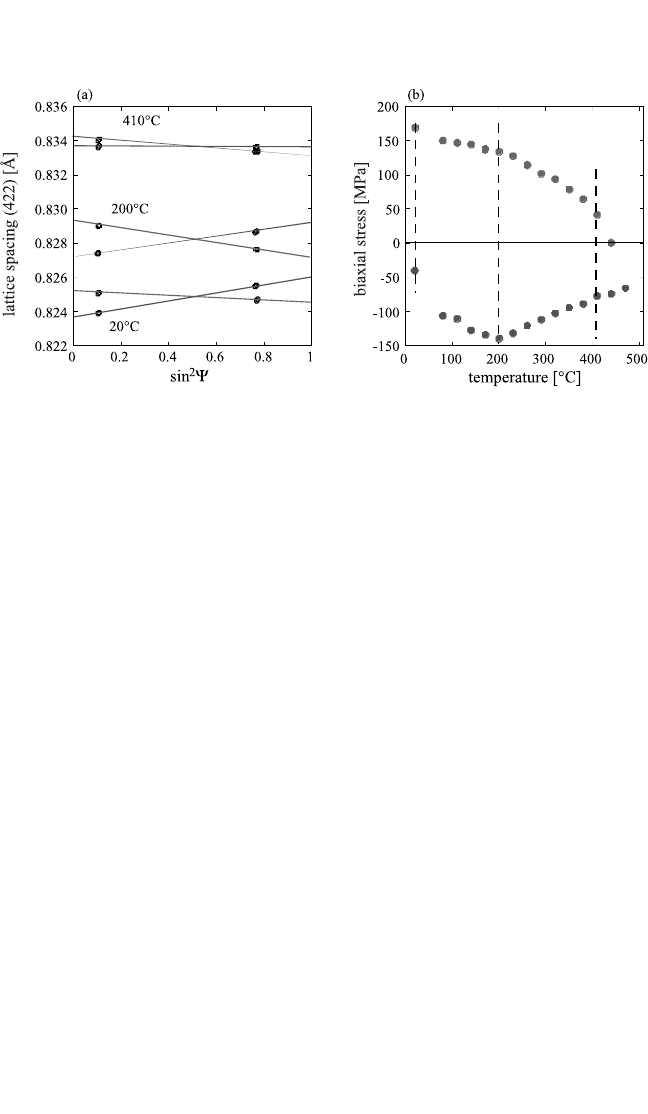
used. This is illustrated in Fig. 8.7(a), which shows a plot of d versus

sin

ψ from measurements on a thin Al film on a Si substrate

[20, 21]

at tem-

peratures of 20, 200, and 440°C. The curves with the negative slopes

were obtained on heating, and the ones with positive slopes on cooling,

indicating compressive and tensile film stresses, respectively. The stress

as a function of temperature obtained from these measurements is shown

in Fig. 8.7(b).

Ch_08.qxd 11/29/04 6:45 PM Page 375

For films with a mixed texture, such as (111) and (100), as often

observed in Cu thin films, measurements for each texture component

become necessary.

[2, 14, 22]

Assuming only minor stress interactions between

the components, the average stress for each orientation can be determined.

Figure 8.8 compares results of wafer curvature and x-ray measurements

on identical samples.

[2, 13]

Apassivated Cu film with 1.0 µm thickness and

a mixed (111) and (100) texture was subjected to a temperature cycle up

to 600°C. As shown, the x-ray method allows the average stress for the

two texture components to be measured, while the wafer curvature tech-

niques give the average film stress.

The details of the stress analysis for films that have other mixed tex-

tures or other crystal structures can be more complicated. Amore detailed

treatment of the sin

ψ method including grain interaction and elastic

anisotropy is given in Clemens and Bain

[18]

and Van Leeuwen et al.

[23]

Finally, it should be pointed out that x-ray measurements can be used to

determine more complex stress states such as those present in narrow con-

ductor lines.

[19, 20, 24]

The x-ray measurements described so far typically use x-ray

beams with a size on the order of mm. As a result, the measured stress

is averaged over many grains. This allows us to study the stress behavior

376 DIFFUSION PROCESSES IN ADVANCED TECHNOLOGICAL MATERIALS

Figure 8.7. (a) Spacing of the (422) lattice planes in a 0.7-µm-thick Al film with a

(111) texture as a function of sin

ψ for three different measurements on heating

and cooling.On heating, the film is under compression (lines with negative slope);

on cooling, it is under tension (lines with positive slope). The intersection of the

lines is associated with the unstrained lattice spacing for each temperature.

(b) Stress as a function of temperature as obtained from the sin

ψ method. Data

from Kraft and Nix.

[21]

Ch_08.qxd 11/29/04 6:45 PM Page 376

STRESSES IN THIN FILMS AND THEIR RELAXATION, KRAFT, GAO 377

of different texture components, but not stress variations from grain to

grain. More recently, several techniques have been developed to meas-

ure stresses with very high spatial resolution.

[25–27]

For some of those

measurements, performed with a submicrometer resolution, white syn-

chrotron x-ray radiation was used. In order to determine stresses, the

deterioration of the Laue diffraction patterns obtained was analyzed.

As an example of such a measurement, Fig. 8.9 shows the stress dis-

tribution in an area of approximately 15 by 15 µm

in a thin Al film as

a function of temperature.

[28]

It can be seen that there are very strong

variations of more than 100 MPa in stress from grain to grain. These

variations may correspond to different orientations, but even for grains

with the same orientation, significant differences in stress are

observed.

Figure 8.8 Stress-temperature evolution in a 1-µm-thick passivated Cu film:

Comparison between the film stress as measured by the wafer curvature tech-

nique and the stress as measured by x-rays in (111)- and (100)-oriented grains.

Data from Baker et al.

[2]

and Keller et al.

[13]

Ch_08.qxd 11/29/04 6:45 PM Page 377

8.3 Stress Relaxation

As described above, the elastic behavior of thin films is basically

understood and does not differ from bulk behavior. In contrast, the plastic

behavior of thin metal films is not well understood and is fundamentally

different compared to that of bulk materials. This section summarizes the

current understanding of thin-film plasticity. Contributions from disloca-

tion plasticity and creep deformation to the relaxation of stresses are dis-

cussed, as well as the experimental evidence.

8.3.1 Experimental Observations

Figure 8.10 shows the stress evolution in Cu thin films on a Si substrate

and exemplifies typical behavior of metal films on low-thermal-expansion-

378 DIFFUSION PROCESSES IN ADVANCED TECHNOLOGICAL MATERIALS

Figure 8.9 Thermal cycling results of a 15  15 µm

area of an Al(Cu) bond pad

(blanket film) showing an averaged biaxial stress component vs.temperature.The

insets show details of the stress distribution in the film at different temperatures.

(The two-dimensional maps are plots of measurements of the in-plane stress.)

Note the large stress inhomogeneities from grain to grain and even within individ-

ual grains. From Tamura et al.,

[28]

with permission.

Ch_08.qxd 11/29/04 6:45 PM Page 378

STRESSES IN THIN FILMS AND THEIR RELAXATION, KRAFT, GAO 379

coefficient substrates. These films have a silicon nitride underlayer and

are either capped by an aluminum oxide layer, which was formed by self-

passivation of a Cu-1 at.% Al film,

[29–31]

or are uncapped. The stresses

were measured by the wafer curvature technique. At the beginning of the

experiment, after sputter deposition and annealing at 600°C, the films are

under tensile stress at room temperature. Because of the larger thermal

expansion coefficient of the film compared to the substrate, the stress

decreases linearly with increasing temperature. The film undergoes both

elastic and plastic deformation during thermal cycling. In general, the

stresses in the capped film are much higher than in the uncapped one

throughout the experiment. At high temperature, this difference has been

attributed to diffusional creep,

[13, 30, 31]

which is active in the uncapped film

and is described in detail in Sec. 8.3.3. The plastic deformation in the

capped film can be assumed to be mediated only by dislocation motion

since the presence of the passivation layer suppresses surface diffusion,

which is required for diffusional creep (Fig. 8.10 and Sec. 3.3). Often, the

stress-temperature evolution is regarded as a measure of film strength as

a function of temperature.

[9]

However, this picture is not completely accu-

rate because the film stress relaxes quite substantially when temperature

is held constant.

[10, 32]

Therefore, the time dependence of the plastic defor-

mation needs also to be taken into account. Furthermore, the stress-

temperature evolution is influenced by strain hardening

[13, 33, 34]

as the film

Figure 8.10 Wafer curvature experiments have shown stress temperature curves

that are strongly dependent on the surface passivation of Cu thin films on sub-

strate. Data are given for pure Cu and Cu-1 at.% Al films where Al tends to seg-

regate toward the surface and form an oxide cap. The film stress was measured

by the wafer curvature technique. Data from Weiss et al.

[31]

Ch_08.qxd 11/29/04 6:45 PM Page 379

is plastically strained; for instance, the total thermal strain for the films

shown in Fig. 8.10 is 0.7% and the plastic strain is about 0.5%.

Beside thermal straining, mechanical properties of thin metal films

have been measured by micro-tensile testing; for example, results have

been reported for Ni,

[35]

Al,

[36]

Cu,

[35, 37]

and multilayered films.

[38, 39]

These

experiments confirmed that thin films exhibit very high yield strength,

which usually increases with decreasing film thickness, grain size, and/or

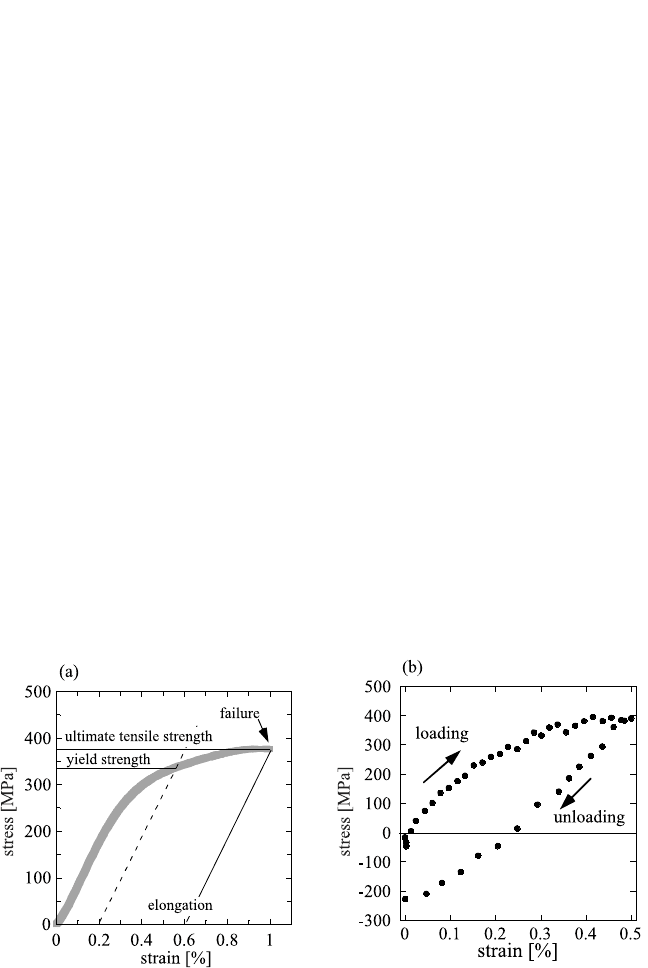
layer thickness in multilayered thin films. As an example, Fig. 8.11(a)

shows the stress-strain curve of freestanding 1.1-µm-thick Cu film.

However, in such tests on freestanding films, the deformation is not con-

strained by a substrate and, furthermore, testing in compression is not pos-

sible. It has been shown that this can be overcome by testing thin films on

a polyimide substrate.

[40]

Figure 8.11(b) shows the stress-strain curve

of such an experiment on a 0.7-µm-thick Cu film obtained using x-ray

measurements. On loading, the film deforms first elastically until yielding

at about 250 MPa is observed. Then, on straining to 0.5%, the flow stress

increases to 400 Mpa, indicating the presence of strain-hardening effects.

On unloading of the specimen, the contracting elastic substrate com-

presses the film, which then undergoes plastic deformation in the opposite

direction. It appears that on reverse loading, the yield strength is some-

what smaller compared to the initial loading. For interpreting mechanical

380 DIFFUSION PROCESSES IN ADVANCED TECHNOLOGICAL MATERIALS

Figure 8.11 Stress evolution as a function of applied strain during tensile tests for

(a) a freestanding Cu film with a thickness of 1.1 µm and (b) for a 1.0-µm-thick Cu

film on a polymer substrate.The film stress for (b) was measured by x-ray diffraction.

Notes: 1. Data for (a) from Read.

[37]

2. Data for (b) from M. Hommel, O. Kraft, and E. Arzt, “A new method to study cyclic deforma-

tion of thin films in tension and compression,” J. Mater. Res., 14(6):2373–2376 (1999).

Ch_08.qxd 11/29/04 6:45 PM Page 380

STRESSES IN THIN FILMS AND THEIR RELAXATION, KRAFT, GAO 381

behavior, the advantage of this test method over thermal straining is

related to the fact that the temperature is not altered during the experi-

ment. In particular, this allows us to attribute the observed asymmetry in

yield stress to hardening effects since any influence from the temperature

change in the thermal cycling experiments is eliminated.

8.3.2 Dislocation Plasticity

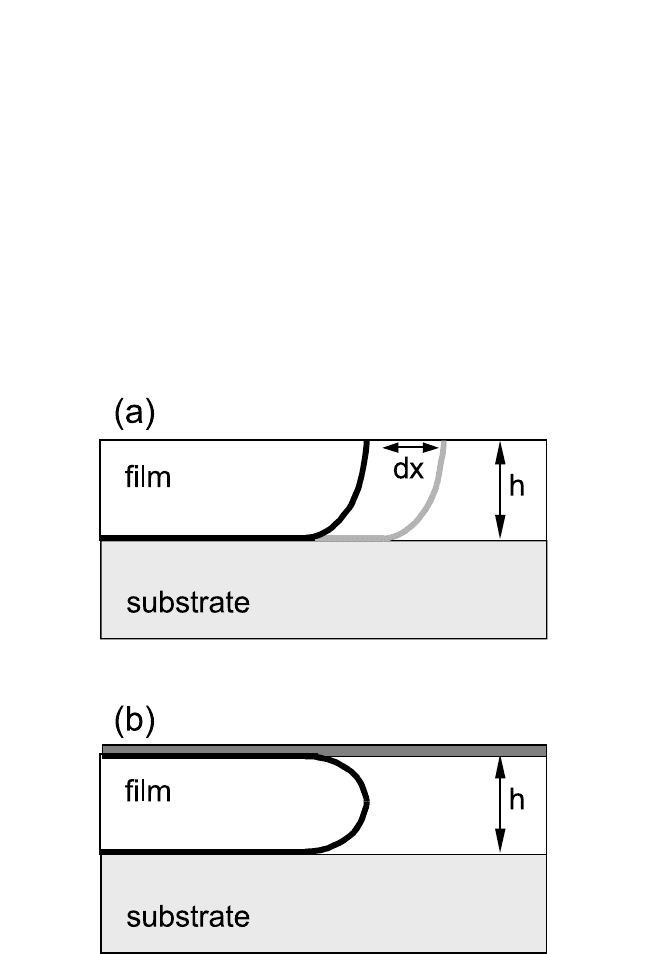
As a start, we consider the motion of a single dislocation in a single-

crystalline thin film attached to a substrate, as shown in Fig. 8.12(a) and

Figure 8.12 Schematic representation of the motion of a single dislocation in a

single-crystalline film, according to the model of Nix and Freund

[1, 45]

for a film with

(a) a free surface and (b) a cap layer. It indicates in (a) that a dislocation segment

with the length dx needs to be created when the dislocation moves by dx.

Ch_08.qxd 11/29/04 6:45 PM Page 381