Gupta D. (Ed.). Diffusion Processes in Advanced Technological Materials

Подождите немного. Документ загружается.

302 DIFFUSION PROCESSES IN ADVANCED TECHNOLOGICAL MATERIALS

heating that may occur. The modalities of nucleation-controlled formation

in the silicides are detailed in the literature;

[26]

some consequences are

summarized below.

With thin films, and experiments conducted at relatively low tem-

peratures, difficult nucleation can affect the order of phase formation. A

case in point is offered by comparing the sequences of phases in Rh and

Ir reactions with Si. The two metals are quite similar and are found just

below one another in the same column of the periodic table. Hence the

respective equilibrium diagrams display remarkable similarities yet are

not totally identical. With either metal, one step in the sequence of phase

formation is the monosilicide (either RhSi or IrSi); then the similarity

ends. With Ir, we observe the formation of Ir

, bypassing two other

phases: Ir

and Ir

. In this case, the ∆G for the formation of Ir

is sufficiently large to allow easy nucleation and the diffusion-controlled

formation of that phase at temperatures lower than necessary to nucle-

ate the two missing phases, with smaller composition changes with

respect to IrSi, and therefore also smaller ∆G changes. With Rh, how-

ever, the list of silicon-rich silicides ends before Rh

, which does not

exist. Then, after the formation of RhSi, we observe the nucleation-

controlled formation of Rh

, curiously with very few nucleation sites,

some 2 or 3 mm apart, visible with the naked eye. Thus we can conclude

that the existence of Ir

prevents the formation of the other phases,

and Ir

A somewhat similar effect is observed in the sequence of phases

during the reaction of Ni films with Si. The sequential formations of

Si and NiSi were considered at the beginning of this section.

Another phase exists, Ni

, that does not appear in the sequence of

phases experimentally observed. In the absence of an explanation for

the failure of that phase to form after Ni

Si, it might be tempting to

assign this failure to some nucleation process; that would at least please

nucleation afficionados. But we do not know. However, once NiSi has

began to form from the reaction of Ni

Si with Si, Ni

would form

from the reaction:

Si  NiSi  Ni

, (22)

with a ∆H  0 ± 9 kJ/mol,

[24]

nearly infinitely small. To the extent that

the phase is thermodynamically stable, the value of ∆G for Eq. (22) has

to be negative. By artificially preparing thin-film samples with an over-

all composition corresponding to Ni

, but composed of adjacent lay-

ers of Ni

Si and NiSi, it has been shown

[47]

that the nucleation of Ni

under the conditions where the two adjacent phases preexist occurs only

Ch_06.qxd 11/12/04 4:05 PM Page 302

REACTIVE PHASE FORMATION, D’HEURLE ET AL. 303

at temperatures above those necessary to form NiSi. In bulk samples

where observations are carried out at temperatures on the order of

800°C, rather than 400°C with thin films, nucleation effects are hardly

noticeable. All anticipated phases are observed to grow, more or less

simultaneously, at least at times sufficiently long to allow observations

in the optical microscope. Yet singularities are observed even then.

[48, 49]

Figure 6.6 is the cross section of a bulk Ni-Si sample heat treated

at 800°C for 6 hours. Anumber of phases are distinguishable, but atten-

tion should be focused on Ni

. The other phases have more or less

planar interfaces, as anticipated in binary systems, but not Ni

which displays a morphology similar to that of the jaws of Tyrannosaurus

rex. It might be tempting to attribute such a singular appearance to

anisotropic diffusion, but that is quite unlikely since this would require

extremely large anisotropy factors. Tentatively, we may propose the

attractive alternative that the cause of the extremely irregular interface

is stress and stress relaxation that occur in very different conditions,

whether at the valley between teeth or at the peak of the teeth. Because

the equilibrium ∆G is so small, even minor changes in elastic (and

possibly plastic) energy would make considerable differences in the

Figure 6.6 Cross section of a Si-Ni diffusion couple after 6 hours at 800°C. Note

the very irregular interface between Ni

and NiSi. From Gülpen.

[48]

Ch_06.qxd 11/12/04 4:05 PM Page 303

304 DIFFUSION PROCESSES IN ADVANCED TECHNOLOGICAL MATERIALS

driving force for growth; hence the unexpected morphology. Initially,

differences in orientation and consequently, differences in anisotropic

stress or diffusion, might be the cause of irregularities that increase in

magnitude as growth proceeds, with stress assuming the primary role.

Because of the small ∆G’s, we anticipate that stress would affect these

nucleation-controlled reactions, so that one of us (d’Heure) has been on

the lookout for such effects for some 30 years, in vain. The bulk growth

of Ni

might have finally provided the smoking gun. We may won-

der whether some strong crystalline anisotropy is necessary for the

development of interfaces such as those observed with Ni

Otherwise, we might expect the same behavior for NiSi

, although in

this case, the chemical (equilibrium) ∆G could be too large to be

affected significantly by variations in ∆H

elas

. In multiphase growth,

however, as difficult as it might be to know small values of ∆G, it is

clear that the value is zero at a eutectic or peritectic point, even if, as a

result, the exact eutectic or peritectic temperature is not known pre-

cisely. In such cases, the nucleation of the corresponding phase (or

phases) is likely to be very difficult. In an otherwise excellent discus-

sion of V-Si reactions,

[10]

that point is not so clearly outlined with

respect to the formation of V

6.2.8 Amorphous and Other Metastable Phases,

Quasicrystals, Ternary Systems

So far, nothing in this discussion has excluded the formation of

metastable phases as a result of reactive diffusion. It has been emphasized

that in the competition for the growth of different phases from reacting

elements, the respective ∆G

’s vary little from each other, at least in com-

parison with the respective D’s. This is also true, for example, of amor-

phous phases, with free energies of formation ∆G only slightly higher than

the corresponding values for the crystalline phases. As a first approxima-

tion, the excess free energy ∆G

excs

 ∆T  ∆S

melt

, where ∆T is the differ-

ence between the temperature T and the melting temperature T

melt

, and

∆S

melt

is the entropy of melting ∆H

melt

T

melt

. Samwer et al.

[50]

and Herr

et al.

[51]

review this subject. Two criteria are usually put forward for the

formation of amorphous phases. The first appears to be thermodynamic, a

high ∆G

of formation for the corresponding crystalline phases; the sec-

ond is kinetic, a high difference in the diffusion coefficients of the two or

three species present in the phase. The second criterion seems to be the

most important and the most direct because crystallization in a binary

system requires that the two elements be mobile. If one element is not

Ch_06.qxd 11/12/04 4:05 PM Page 304

REACTIVE PHASE FORMATION, D’HEURLE ET AL. 305

mobile, the phase can grow via the motion of the mobile element, but once

grown, it will remain in an amorphous state until the sample is brought to

a temperature high enough to allow the motion of the slow-moving

element. This is well typified by the growth of thermal SiO

, which grows

via the very fast interstitial diffusion of molecular oxygen in the SiO

net-

work, while the Si atoms with an activation energy for motion of the order

of 5 eV are totally immobile at temperatures below 1100°C. That is sim-

ple enough.

The first criterion, a high ∆G

of formation, has a direct thermody-

namic implication: The sum ∆G

 T∆S

melt

has to remain negative for

the phase to grow, even in a metastable amorphous condition. But this

high ∆G

of formation has two important kinetic implications as well.

Ahigh ∆G

of formation implies, in general, a high T

melt

, so that at ordi-

nary temperatures (much below T

melt

), the atomic mobilities will be

small, making any crystallization difficult. To be sure, a high T

melt

implies a high driving force for crystallization at a low temperature T,

as the force increases linearly with the difference T

melt

 T, while the

atomic mobility necessary for crystallization decreases as some expo-

nential function of that difference. Moreover, there is a second aspect

to this: A high ∆G

of formation implies almost necessarily a large dif-

ference in atomic mobilities in any compound that is not equiatomic

(type AB). This is so because, while the majority of atoms can usually

diffuse along their own network without undue interference, the motion

of the minority atoms often requires that these occupy the sites of

majority atoms. This requires the local destruction of the structure of

the growing phase and an excess activation energy for motion equal to

at least a fraction of the free energy of formation; hence, the higher the

latter, the bigger the difference in mobilities between the two atomic

species.

[21]

This is the prime criterion for the growth of an amorphous

phase.

A brief exploration of the literature shows that the mostly kinetic

conditions that govern the reactive formation of amorphous phases do

not apply for the formation of other metastable phases. The formation of

the metastable Ni

already discussed

[36, 37]

seems to depend not on

kinetic details but on the complex details of the nucleation process. That

a compound with a corresponding composition is a stable phase in the

Co-Al system confirms suspicions that Ni

is not far from being sta-

ble also, so that even a minor decrease in surface or elastic energy would

be enough to stabilize that phase in preference to the stable NiAl

. The

formation of NiSi with the NiAs structure epitaxial on (111) Si is clearly

dictated by the low interfacial energy,

[52]

not by considerations about the

relative mobilities of Ni and Si. The same is true of the formation of

FeSi

and other Fe silicides with the CaF

structure.

[53]

These phases

Ch_06.qxd 11/12/04 4:05 PM Page 305

306 DIFFUSION PROCESSES IN ADVANCED TECHNOLOGICAL MATERIALS

tend to transform to the stable form beyond a critical thickness where

the constant “gain” due to a low interface energy becomes lower than

the increasing “loss” (proportional to the thickness) due to the

metastable phase.

Some of these metastable phases do not form initially, but after other

phases have already formed, for example, Ni

Si before NiSi. Two

metastable phases were observed in the reaction of Al with Pt, after an

amorphous phase was formed initially.

[54]

We have already alluded to the

formation of quasicrystalline phases.

[25]

Further information is contained

in the proceedings of symposia.

[55, 56]

In Al-Pd reactions,

[37]

the stable

phase Al

was observed to grow prior to the decagonal quasicrystalline

Pd. During the reaction of Co with Al, the stable Co

grows first,

then a decagonal phase Co

[57]

For this phase, it has been shown

[57–59]

that 1) the enthalpy released during its formation is within experimental

errors equal to that expected for the stable phase; 2) changes in thickness

do not affect the phase sequence and do not suppress its formation; 3) an

increase in temperature causes the formation of the stable phase. A low

interface energy and, therefore, preferential nucleation are presumed to be

at the origin of the formation of such quasicrystalline phases.

[55, 56]

Few

words are more randomly misused in the literature than the word “stable.”

In the same vein, care should be taken with the expression metastable: In

the reaction of Au with amorphous Si,

[60]

we can form compounds that are

metastable with respect to thermodynamic equilibrium, yet are stable with

respect to amorphous Si, since they form with a negative enthalpy of

formation.

Reactions in ternary systems deserve more attention; they constitute

a subject in themselves. Reactions between Ni and SiC are considered

by Lien et al.

[46]

and Gas et al.

[47]

Aspects of the reaction of Ti with Si-Ge

are analyzed by Thomas et al.

[61]

and Aldrich et al.

[62]

Kodentsov et al.

[63]

and Loo

[64]

discuss ternary reactions in general. All that has been writ-

ten, of a more or less theoretical character, implies that researchers are

working with very pure materials. Impurities even in small quantities

may change the character of the reactions from that of a binary to a ter-

nary or higher order system, with serious consequences. Impurities may

affect kinetics by forming more or less porous diffusion barriers, or by

reducing grain boundary diffusion. In the reaction of Si with commer-

cial Fe, different results are obtained with different grades of Fe (see

Shimozaki et al.,

[65]

Fig. 2). Single-phase growth (Fe

Si) is observed in

one case, and multiple-phase growth in the other. (The explanation

given by the authors may or may not be correct.) Similarly, the reaction

between Mo and Si should lead to multiphase growth, contrary to the

report of the formation of MoSi

only.

[9]

Ch_06.qxd 11/12/04 4:05 PM Page 306

REACTIVE PHASE FORMATION, D’HEURLE ET AL. 307

6.2.9 Other Effects: Grain Boundaries and

Impurities, Diffusion Coefficients

Varying with Composition

In general, with binary systems, the interfaces remain planar and par-

allel to themselves. This has been observed to be true with silicide phases

such as NiSi and PtSi, and less true with phases whose formation is

nucleation-controlled, such as NiSi

. Effects due to grain boundary dif-

fusion can often be neglected, but not always. Astudy of Au-Cu interac-

tions at about 200°C in thin films

[66]

did not lead to publication because

the interactions were dominated by the very fast intergranular diffusion

of Cu inside the Au film, which made any kinetic interpretation

extremely ambiguous. A similar effect with Al films had serious practi-

cal implications for electromigration. We can delay electromigration fail-

ures in Al thin-film conductors, by forming a continuous intermetallic

layer

[67, 68]

of Al with some transition metal in parallel. Because of the

considerably smaller diffusion coefficients in such layers, they remain as

an electrical bridge in those regions where failure has already occurred in

the adjacent Al film with its relatively high diffusion. When attempting

to form a thin continuous layer of an intermetallic compound between,

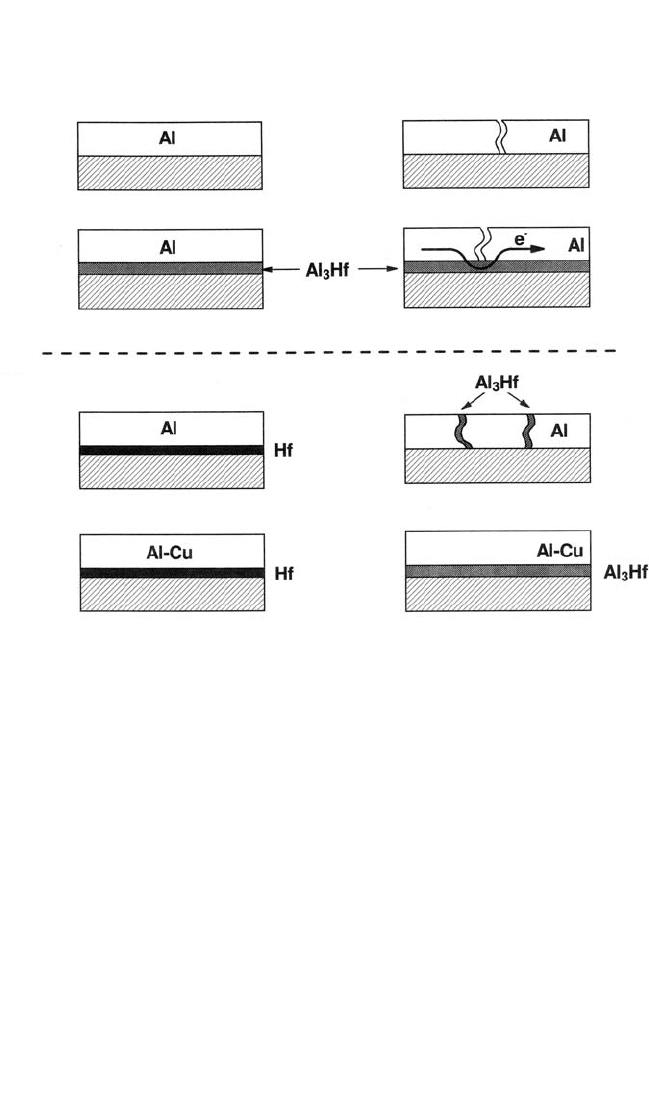
for example, Al and Hf, it was observed that the compound formed pref-

erentially along the grain boundaries of the Al film, and thus could not

act later as the desired electrical bridge (see Fig. 6.7). Continuous inter-

metallic layers, however, could be formed if, instead of using pure Al,

one uses Al alloyed with Cu, which is known to reduce grain boundary

diffusion in Al. Indeed, this alloy addition is used to retard electromigra-

tion failure in Al thin film conductors by a factor of about 50.

[69, 70]

The

grain boundary impurity effect being considered here is quite general:

Impurities segregate to grain boundaries, thereby lowering the grain

boundary energy, and simultaneously increasing the activation energy for

grain boundary diffusion and decreasing the diffusion coefficient.

[71]

This

effect is mentioned again later. There is also an interesting experimental

mode where diffusion does not proceed in a direction normal to the inter-

face, as in ordinary diffusion couples; instead, it occurs along the lateral

dimension of a thin film. A very good example referring to Al-Ni reac-

tions is provided by Liu et al.

[72]

This discussion of the reactive phase formation has assumed that the

diffusion coefficient in the growing layer is either constant in each grow-

ing layer from one interface to the other, or that some average value pro-

vides a valid approximation. In some cases, this assumption leads to an

erroneous interpretation. In the thin-film reaction of Al with Ni at about

100°C,

[73]

it was observed that the central phase, NiAl, did not appear as a

Ch_06.qxd 11/12/04 4:05 PM Page 307

308 DIFFUSION PROCESSES IN ADVANCED TECHNOLOGICAL MATERIALS

single phase. Instead, it was divided into two regions, each with a com-

position corresponding to the extreme limits of stability, about 45 and 55

at.% Ni. This effect is not actually due

[74]

to some thermodynamically

mandated phase separation; it is the simple result of kinetics, because the

diffusion coefficients at these two extreme compositions are immensely

higher than at the central composition (50 at.%). Since phases grow only

at interfaces, the flux of atoms, proportional to D  dmdx, must be con-

stant from one interface to the other. If in some region of the growing

phase D is very small, a constant flux is achieved by making the gradient

dmdx very large. For example, in the case of NiAl, the phase does not

grow at the stoichiometric composition where the diffusion coefficient is

Figure 6.7 Schematic representation of the effect of a layer of transition metal

compound on electromigration in Al thin-film conductors. From left to right: In

(A), the presence of a layer of intermetallic compound provides an electrically

continuous path, even after failure of the Al conductor itself. In (B), with pure Al

the product of the reaction between Al and a transition metal tends to be scat-

tered along the grain boundaries of the Al film, but a continuous layer is

obtained if the Al is alloyed with Cu, which reduces grain boundary diffusion in

Al. Not to scale.

(A)

(B)

Ch_06.qxd 11/12/04 4:06 PM Page 308

REACTIVE PHASE FORMATION, D’HEURLE ET AL. 309

the smallest. Another example, Fe-Si, has been discussed by d’Heurle

et al.

[75]

At least in some phases with very narrow composition limits, the

diffusion coefficient is likely to be a very strong function of composition,

but the resulting effect may not be observable.

Following considerations of a more or less theoretical character, some

very practical effects in silicide thin films are examined in Section 6.3.

Before doing so, let us recall some topics of general interest. Thin-film

studies of interactions of Al or Au with transition metals

[76, 77]

demonstrate

the following: (1) The first phase to form (there as well as elsewhere) is

one that is rich in the metal with low melting point (either Al or Au).

(2) This phase grows by the motion of the species with the low melting

point, as mandated by the ordered Cu

Au rule.

[21]

This rule (1) does not

apply so clearly to silicides because during reaction, Si undergoes a state

transformation (from covalent with coordination number 4 to a much

more metallic state with coordination number 10). For example, in TiSi

Si has little similarity with elemental Si (unlike, for example, Ni in Ni

Al).

For more information, it would be worthwhile to consult

Schmalzried’s general book,

[78]

although it is a little heavy on ionic solids

for our purpose. The general equations for multiple phase growth have

already been mentioned.

[7, 8]

There are several good reviews of thin-film

silicides formation.

[21, 79, 80]

For reactions in bulk samples, there are some

earlier investigations on the formation of Al-Ti

[81]

and Ni-Al

[82]

inter-

metallics, and some recent ones on Ni-Si

[49]

and Co-Si

[83]

silicides.

Diffusion in silicides

[84]

and in intermetallic compounds in general

[85–87]

have also been discussed.

6.3 Practical Problems in Electronic

Technology

This section discusses some practical aspects of the use of com-

pounds formed via reactive diffusion in the electronics industry. Quite a

few of the problems currently encountered with these materials directly

illustrate some of the issues discussed in Section 6.2. Others comple-

ment aspects that were not fully developed. For example, for VSi

WSi

, the mode of reaction does not fit neatly in the other two categories

of diffusion-controlled and nucleation-controlled reactions. Considerations

about the formation of TiSi

will allow examination of a class of sili-

cides once called “ill-behaved”.

[16]

Although the appellation has not met

with great success, there are good reasons to believe that it remains

valid.

Ch_06.qxd 11/12/04 4:06 PM Page 309

310 DIFFUSION PROCESSES IN ADVANCED TECHNOLOGICAL MATERIALS

6.3.1 Titanium Disilicide, Activation Energy for the

Motion of the Interface Between the C49 and

C54 Phases, Nucleation of the C49 Structure

For many years, the interconnections between devices in integrated cir-

cuits were made of highly doped polycrystalline Si. This material has a num-

ber of serious advantages. For one thing, it was ideally suited for processing

on Si substrates from which active devices are fabricated. Moreover, it was

also quite ideally suited as electrode material over the SiO

gate of insulated

gate field effect transistors (FETs). About 25 years ago, with device dimen-

sions approaching 1 mm, the resistance of even highly doped polycrystalline

Si became too high, causing unacceptable IR (current × resistance) drops and

RC (resistance × capacitance) time delays. Substitute materials must also be

compatible with existing fabrication processes, which ideally might include

exposure to high temperatures (of the order of 1000°C) for diffusion, or the

activation of dopants in the active part of the devices. Silicides fulfilled most

of the requirements: resistance to oxidation, a conductivity considerably

higher than that of polycrystalline Si, resistance to some etching solutions,

and the ability to withstand exposure to high temperatures without suffering

serious damage to their shape and physical properties. One of the first sili-

cides used was WSi

. However, following the discovery that the resistivity of

TiSi

(20 mΩ.cm) was about one-third to one-fourth that of WSi

[88]

this com-

pound became and remained for many years the favored silicide for use in

integrated circuits. (The resistivity values referred to here are those that are

encountered in thin-film applications, not necessarily the values obtained

with single crystals of high purity.) Because of the technical applications, the

literature on TiSi

films is enormous. Yet in spite of much effort, a good

understanding of the behavior of TiSi

remains wanting. Two aspects of this

behavior are analyzed here.

Unfortunately, when forming TiSi

from the reaction of Ti films with

Si, or during the crystallization of amorphous TiSi

obtained from the

codeposition of Ti and Si, it is not the low-resistivity structure of TiSi

C54, that forms first, but the C49 structure, with a resistivity about three

or four times higher. The reason for this is not clear, but it may be due to

the fact that the mobile species in TiSi

, Si (in agreement with the ordered

Au rule), has a higher mobility in the C49 than in the C54 phase.

[89]

Also, the elastic constants of the C49 phase have been reported

[90]

to be

lower than those of the C54 phase, which would lead to smaller stress

effects (∆H

elas

). It is likely that the C49 structure is metastable, although it

is the stable form of the closely related ZrSi

and HfSi

. The low resistiv-

ity phase is the desired one, and it requires heat treatment at a temperature

sufficiently high to allow the nucleation and growth of the C54 phase via

Ch_06.qxd 11/12/04 4:06 PM Page 310

REACTIVE PHASE FORMATION, D’HEURLE ET AL. 311

a paramorphic transformation (the term allotropic being reserved for the

transformations of elemental phases) driven by a small difference in free

energy. The experimentally determined enthalpy change for this transfor-

mation is reported to be 1.5 kJ/mol.

[91]

This is commensurate with the

driving force for the nucleation of the C54 phase, and then for its growth.

The point has been made that in the reaction between phases, if the com-

position difference is small, for example, Eq. (22), the corresponding ∆G

is also small. Here, the limit is reached when, in a paramorphic transfor-

mation, there is no change in composition at all. With respect to nucle-

ation, the condition remains the same as before; namely, from a small ∆G

it ensues that nucleation is difficult and the density of nuclei small. That

is no problem with blanket films that transform at temperatures in the

vicinity of 700°C, about 150 K above the temperature required for the for-

mation of C49. However, when the width of the thin-film conductors

decrease below about 0.3 mm, it is observed that for a given heat treat-

ment, some conductors do not transform at all, while others may trans-

form only partially.

[92]

That is not tolerable. Apartial remedy is to increase

the heat treatment temperature, but engineering constraints prevent this

approach. One of the constraints, which is built into the conductors them-

selves, is that with films 10 nm thick, exposure to high temperatures

causes the film to agglomerate into individual islands to minimize the sur-

face energy. The temperature at which this occurs may fall below that

required for nucleation. Many recipes have been used to try to alleviate

these difficulties. Since a good account of these is given elsewhere,

[93]

they are not considered here. Rather, some quantitative aspects of the

nucleation and growth process are discussed. The increase in temperature

(akin to superheating) necessary to nucleate the C54 form of TiSi

has a

close equivalent in the classical example of the solidification of liquid

metals, where the solidification of mercury requires increased undercool-

ing as the liquid metal is divided into droplets of decreasing size.

[94]

Many attempts have been made to understand the intricacies of the

nucleation and growth of the C54 phase of TiSi

. Different authors arrive

at the same conclusion: a very high activation energy of about 4 eV. The

most recent and complete study is based on mapping the new grains via

micro-Raman scattering as well as electrical resistance measurements.

[95]

(The two coincide quite nicely.) The analysis was carried out according to

a modified form of the Johnson-Mehl-Avrami method because the direct

JMAmethod did not provide a good account of the evolution of the nucle-

ating centers during the process of nucleation and growth. The study led

to values of apparent activation energies, ∆G*, ∆G*

kin

, and ∆G

mot

, for

growth (the motion of the interface between C49 and C54) of the same

order of magnitude, about 4 eV. Therefore, ∆G*

should be quite small,

perhaps about 0.5 eV. Avalue of ∆G

mot

of 4 eV for a material with a melting

Ch_06.qxd 11/12/04 4:06 PM Page 311