Gupta D. (Ed.). Diffusion Processes in Advanced Technological Materials

Подождите немного. Документ загружается.

Ch_05.qxd 11/29/04 6:20 PM Page 282

6 Reactive Phase Formation:

Some Theory and Applications

François M. d’Heurle and Christian Lavoie

IBM T. J. Watson Research Center, Yorktown Heights, New York

Patrick Gas

Université d’Aix-Marseille, Marseille, France

Jean Philibert

Laboratoire des Matériaux, Université de Paris-Sud, Orsay, France

6.1 Introduction

In general, the expression “reactive phase formation” encompasses all

phenomena whereby the reaction between two adjacent phases leads to

the formation of one or several product phases. However, it is usually lim-

ited to cases where at least one of the reactants is solid, and that reactant

acts as a substrate for the formation of a new solid phase. In current elec-

tronic technology, examples of such reactions would be the thermal oxidation

of Si, the reaction of a metal film with single-crystal or polycrystalline Si

to form one or several silicides, and the reaction of Cu, Ni, Au or some

alloy thereof with Sn during soldering. Such phenomena are not only

important in electronic technology; they are encountered in an endless

variety of conditions, as in the high-temperature reactions between finely

divided oxide particles to form cements. Limoge and Boquet

[1]

provide

excellent general information about such phenomena.

This chapter is composed of two main sections. In Section 6.2, the

modalities of reactive diffusion are considered from a more or less theo-

retical point of view. The conditions leading to linear or linear-parabolic

kinetics are analyzed, as well as those leading to nucleation-controlled

reactions. A distinction is made between the formation of intermediate

phases from reacting elements, which seems dominated by kinetic effects

(diffusion), and subsequent reactions, when new phases are born from

already formed phases. Then nucleation can play the dominant role in the

process of phase formation and, in some cases, in the absence of such for-

mation. Section 6.2 considers the process of phase formation with sili-

cides that are of current technical importance in the electronics industry:

TiSi

, CoSi

, and NiSi. This discussion either illustrates some of the points

made in the earlier theoretical section, or complements such points, as

when considering ternary effects with alloyed CoSi

. Most of the effects

reported are well established. However, in order to be up to date, some

Ch_06.qxd 11/12/04 4:05 PM Page 283

284 DIFFUSION PROCESSES IN ADVANCED TECHNOLOGICAL MATERIALS

tentative explanations are advanced in considering the nucleation of the

C49 phase of TiSi

, or enthalpy effects in solutions of CoSi

and NiSi

This chapter is limited to binary systems, except for short references to

ternary ones such as the solid solutions just mentioned.

6.2 Theoretical Considerations

6.2.1 One Phase Growing, Diffusion Controlled

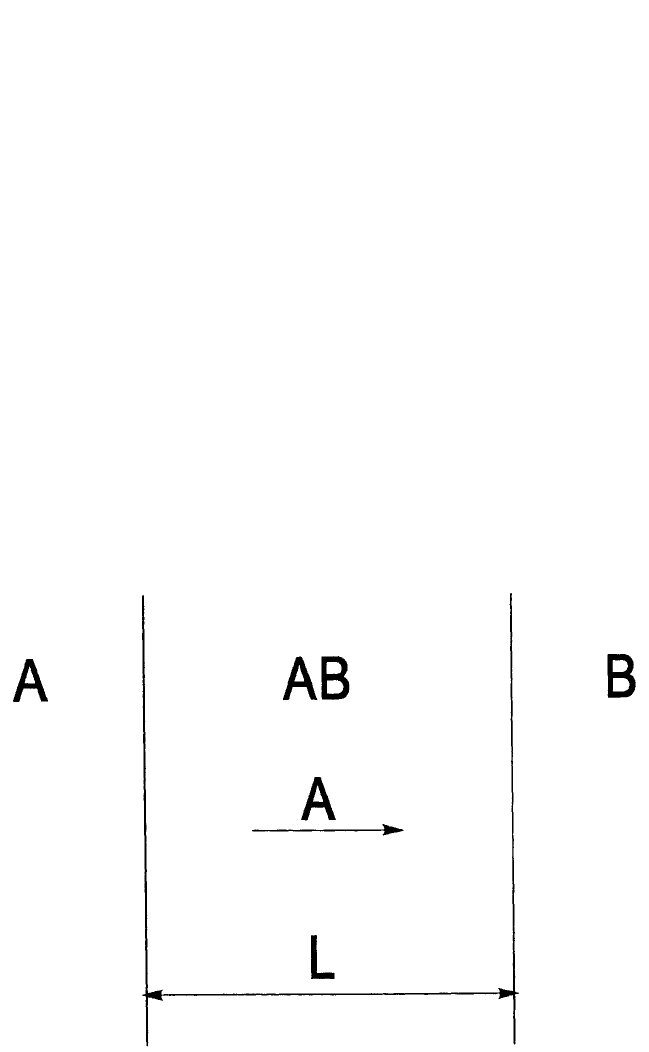
This chapter assumes that all phases are solid, so that, as sketched in

Fig. 6.1, the reaction of A with B results in the growth of a compound

according to:

mA  nB  A

(1)

that is driven by a decrease of free energy ∆G per mole of A

. It is often

true that the growth of such compounds is dominated by the motion of only

one atomic species, here assumed to be A. The atomic flux of A atoms j

Figure 6.1 Schematic representation of a single phase (here, for example, AB)

growing from the reaction of two elements, A and B. It is assumed that only the A

atoms are mobile in the growing phase.

Ch_06.qxd 11/12/04 4:05 PM Page 284

REACTIVE PHASE FORMATION, D’HEURLE ET AL. 285

across the growing layer (that is responsible for its growth) can be written as:

N

 (D

kT)  (dm

dx), (2)

where N

is the density of A atoms in the compound (number of A

atomscm

); D

is the diffusion coefficient of A atoms in A

, so that

according to the Einstein formulation, D

kT is the mobility of these A

atoms; and dm

dx is the driving force on these atoms, the chemical

potential gradient. (Be careful; it is not the self-diffusion coefficient of A

atoms in an Amatrix. Although this is obvious, mistakes are often made.)

If D

is constant across the whole thickness of the growing layer, or is a

value averaged over the thickness Lof the layer, Eq. (2) can be written as:

N

 (D

kT)  (∆G

L), (3)

where ∆G

 ∆Gm, the change of free energy accompanying the transfer of

one mole of Aatoms from one interface to the other and resulting in the for-

mation of 1m mole of A

. If Vis the volume per mole of A

, the trans-

fer of a mole of Aatoms across the layer causes an increase in the volume of

the growing layer of V

, equal to Vm. Since the rate of growth of the layer

dLdt is equal to the product j

 V

, and N

 mV, Eq. (3) yields:

dLdt (D

kT)  (∆G

L). (4)

Hence, L is proportional to t

12

, implying parabolic growth controlled by

diffusion. To be accurate, we should pay attention that the equivalence

between dm

dx and ∆G

L in going from Eqs. (3) to (4) is precise only

when the solubility limit of B in Ais very low, and the range of composi-

tion of A

is very narrow. In general, if the reactant and the product

phases are solid, the usual relation ∆G  ∆H is valid, so that we can use

enthalpy values (enthalpy of formation) if free energies are not available.

Writing Eqs. (1) through (4) required making a number of assumptions

that may not be valid in all cases: (1) that the solubility limits in both A

and B are small (negligible), and (2) that the concentrations of A or B

atoms do not vary significantly from one interface to the other.

The treatment here follows the Nernst-Einstein Eq. (2) rather than the

more usual Fick’s law. One advantage is that in Eq. (2), the various factors

that contribute to j

are clearly separated and easily identifiable. Another

advantage is that if additional forces are applied to the moving atoms, for

example, in electrical, stress, or magnetic fields, they can simply be added to

∆G

L, provided that the forces are expressed in the correct units. That

cannot be done, except with extreme care, using Fick’s formulation, and

carelessness may lead to extremely erroneous conclusions. Using Fick’s law,

N  D

 (dc

dx), (5)

Ch_06.qxd 11/12/04 4:05 PM Page 285

286 DIFFUSION PROCESSES IN ADVANCED TECHNOLOGICAL MATERIALS

and using the same procedure as for the derivation of Eq. (3) from Eq. (2),

we obtain:

N  D

 (∆c

L), (6)

where D

is the Fick’s coefficient of diffusion for species A; ∆c

(dimensionless) is the change in concentration from one interface to

another; and N is the atomic density in the compound. One of the prob-

lems with the use of Fick’s law is that generally ∆c

is poorly known,

particularly when it is very small. Unfortunately, reliance on Eq. (6) has

led to statements in the literature to the effect that in comparing the rates

of growth of two intermediate layers, the one with the greatest ∆c

(or

the equivalent ∆c

) will have the fastest rate of growth, which is absurd.

For example, for a phase with composition limits very close to each

other, namely, with ∆c approaching zero, a finite rate of growth would

be possible only if D

became nearly infinitely big, which is clearly a

physical impossibility. In reality, D may increase significantly with

deviations from stoichiometry (because of the formation of defects,

vacancies, and antisite atoms), as in AlNi

[2]

or AlCo,

[3, 4]

but then the

increased growth rate results from the extremely high value of D, not

from the minimally increased value of ∆c

. When writing Fick’s rela-

tion, Eq. (5), the diffusion coefficient was written with the superscript F

to distinguish it from D, truly D

, in the Nernst-Einstein formulation

[Eqs. (2) through (4)]. The two coefficients, D

and D

, are not equal

at all, except in the case of ideal solutions, which have little to do with

the intermediate compounds presently under consideration. The Nernst-

Einstein coefficient is the coefficient measured if we follow the diffu-

sion of a radioisotope of A in A

, and is thus truly representative of

the diffusion of that element in the compound. Years ago, Herring

[5]

pleaded for expressing diffusion relations in terms of free energy rather

than concentration: “It has long been recognized that it is more appro-

priate to write the diffusion equations for multicomponent systems with

chemical potentials, or their equivalents, rather than with concentra-

tions, and this fact has recently been the subject of a number of papers

in the metallurgical literature. The most recent, and probably the most

satisfactory, of these is that of J. Bardeen.

[6]

” In spite of the justly earned

reputation of the two authors, what they had to say on this subject

remains largely ignored, 50 years later.

If both atomic species are mobile simultaneously in the growing

compound, we would simply add the contribution of the B atoms to the

overall growth rate:

dt  (D

kT)  (∆G

L). (7)

Ch_06.qxd 11/12/04 4:05 PM Page 286

REACTIVE PHASE FORMATION, D’HEURLE ET AL. 287

With ∆G

 ∆Gm and ∆G

 ∆Gn, the sum of Eqs. (4) and (7) yields:

dLdt  [1(kTL)]  (1c

 1c

)  (c

 c

)

 [∆G(m  n)],

(8)

where the concentration c

(not per unit volume, but from 0 to 1) of A

atoms is m(m  n), that of B atoms n(m  n), c

 c

is the well-

known Darken coefficient of diffusion, and ∆G(m  n) is the free energy

change per g atom (Avogadro’s number of atoms, not per mole of com-

pound) upon reaction 1.

6.2.2 Two Phases Growing Simultaneously,

Diffusion Controlled

Afairly complete analysis of this subject is presented in the literature

[4]

for readers who want a more thorough presentation than the one offered

here. In reacting two elements A and B together, we might anticipate the

simultaneous growth of all the phases present in the equilibrium diagram

at the temperature at which the reaction is being carried out. For such a

general case, we usually refer to two treatments,

[7, 8]

but there are others,

for example, specifically on Mo-Si

[9]

and V-Si

[10]

reactions. Here we consider

only two phases, A

and A

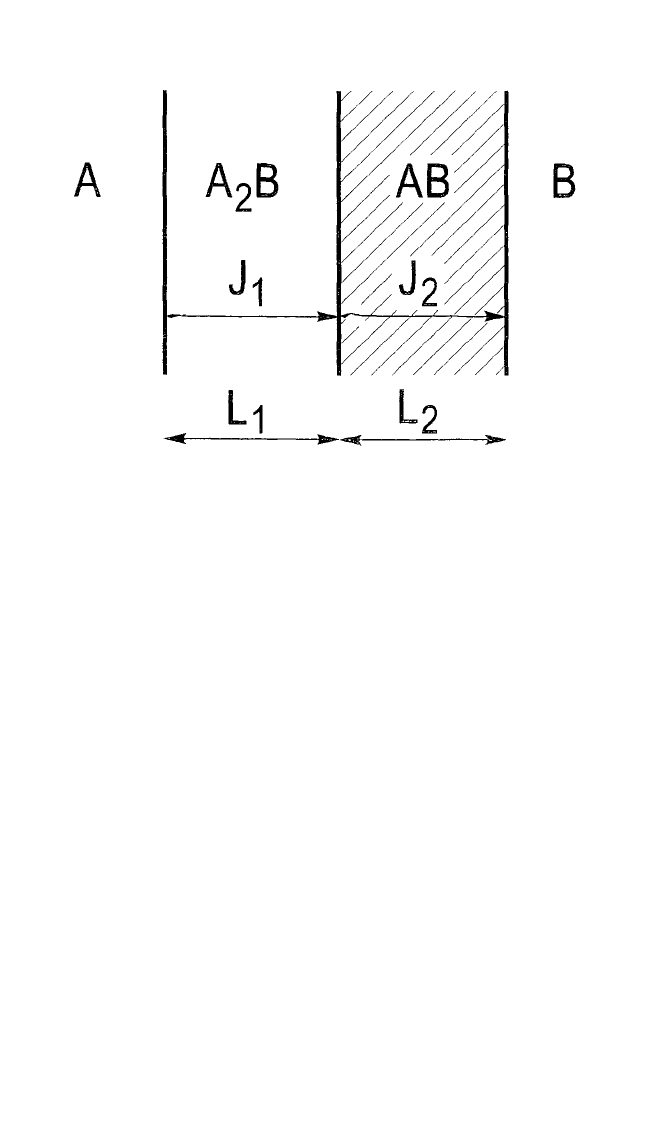
, growing simultaneously, as illustrated in

Fig. 6.2. In this case, the growth of either one of the two phases is depend-

ent (again assuming that only the Aatoms are mobile) not only on the flux

of atoms in the one phase, but also on the flux in the other phase. This is

because each phase simultaneously grows at the expense of the other

phase and is consumed by that phase. Hence:

dt → f(j

 j

), (9)

where the subscripts 1 and 2 refer to the two growing phases.

In writing the expression for j

, care must be taken that the force on

the moving atoms is no longer ∆G

obtained from Eq. (1), but ∆G

cor-

responding to Eq. (10), since the A-rich phase 1 does not grow from B but

from the relatively A-poor phase A

(nq)A

 [m  (npq)]A  A

. (10)

The diffusion coefficient D

Α1

) remains the same as previously,

, since phase 1 remains identical to itself, although not entirely. Were

we to use Fick’s law, care should be taken that ∆c

for two-phase

growth is somewhat smaller than ∆c

for single-phase growth, because

Ch_06.qxd 11/12/04 4:05 PM Page 287

288 DIFFUSION PROCESSES IN ADVANCED TECHNOLOGICAL MATERIALS

in this latter case, A

would be taken as in equilibrium with B, and in

the other with A

. However, D

would still be different from D

From Eq. (10),

∆G

 (1m)  [∆G

fAmBn

 (nq)  ∆G

fApBq

)], (11)

where ∆G

fAmBn

is the free energy of formation of one mole of A

, the

same as ∆G for Eq. (1), and ∆G

fApBq

is the free energy of formation of

. In general, ∆G

will not be too different from ∆G

, perhaps a fac-

tor of 2 or 3, which is small with respect to variations in D’s; for exam-

ple, D

versus D

, which may differ by several orders of magnitude.

But that is not always true. A brief mental estimation shows that if the

difference in composition between A

and A

is small, for example,

m  n  1, and p and q to 4 and 5, respectively, ∆G

can be very small,

and the product D

 ∆G

is very small also. Thus thermodynamics

may affect the rate of growth of a phase, depending on whether it is

growing alone or in competition with other phases; that is true even if

such growth effects are dominated by variations in D values from phase

to phase.

In calculating ∆G

for the flux of A atoms in phase 2, we should

consider that the motion of A atoms results in the formation of A

theA

A

interface by removal of Aatoms from A

, as well as at the

Figure 6.2 Schematic representation of two phases (here, for example, A

B and

AB) growing simultaneously from the reaction of A with B. It is assumed that only

the A atoms are mobile.

Ch_06.qxd 11/12/04 4:05 PM Page 288

REACTIVE PHASE FORMATION, D’HEURLE ET AL. 289

B interface by the addition of A atoms to B. With proper care, the

simultaneous growths of the two phases can be expressed as:

dt  aL

 bL

(12a)

and

dt  dL

 gL

. (12b)

It is easy to show that L

, L

, and L

 L

are all proportional to t

12

;

growth remains parabolic, and the phases start to grow at time zero.

The terms a and d are equal to, or of the form, D

 ∆G

and D



∆G

, respectively. If w is the ratio of the volumes per A atom in

phases 1 and 2, equal to V

V

, then b and g contain, in addition to

the terms found in a and d, the factors w and 1w, respectively. This

is because b and d correspond to the effects of diffusion in phases 2

and 1 on the growths of phases 1 and 2. The simultaneous growths of

phases 1 and 2 require that Eqs. (12a) and (12b) should be positive,

which leads to:

ab  L

L

 gd. (13)

If the differences between a,b, g, and d are entirely dominated by dif-

ferences between D

and D

, or in general between D

and D

(includ-

ing terms for the diffusion of B atoms), then L

L

should be a function

of D

D

. If that ratio is big, at the beginning when L

remains small,

, although mathematically greater than zero, would remain physically

meaningless if smaller than about 1 nanometer. Actually, phases may

not start to grow simultaneously, even in the case of pure diffusion-

controlled growth. That may not always be due to purely kinetic fac-

tors, since thermodynamics may also dictate occasionally that some of

the terms a, b, g, and d differ widely from one another. Calculations

[6]

show that the ratio L

L

is a constant from time zero if we start with

pure Aand B, and tends toward this constant if the sample is artificially

modified, for example, by the insertion of some phase 1 or 2 between

Aand B. Physically, things may behave differently for a number of rea-

sons. Consideration of Eqs. (l2a) and (12b) reveals that, if such a sam-

ple were prepared, the rate of growth of the inserted phase at time zero

should be negative. It also follows from these two equations that, math-

ematically, an existing phase cannot be made to disappear, because

when the thickness of a phase tends towards zero, its rate of growth

tends toward infinity.

Ch_06.qxd 11/12/04 4:05 PM Page 289

290 DIFFUSION PROCESSES IN ADVANCED TECHNOLOGICAL MATERIALS

6.2.3 Linear Parabolic Kinetics, One-Phase Growth,

Oxides, Equilibrium, Plotting of Data

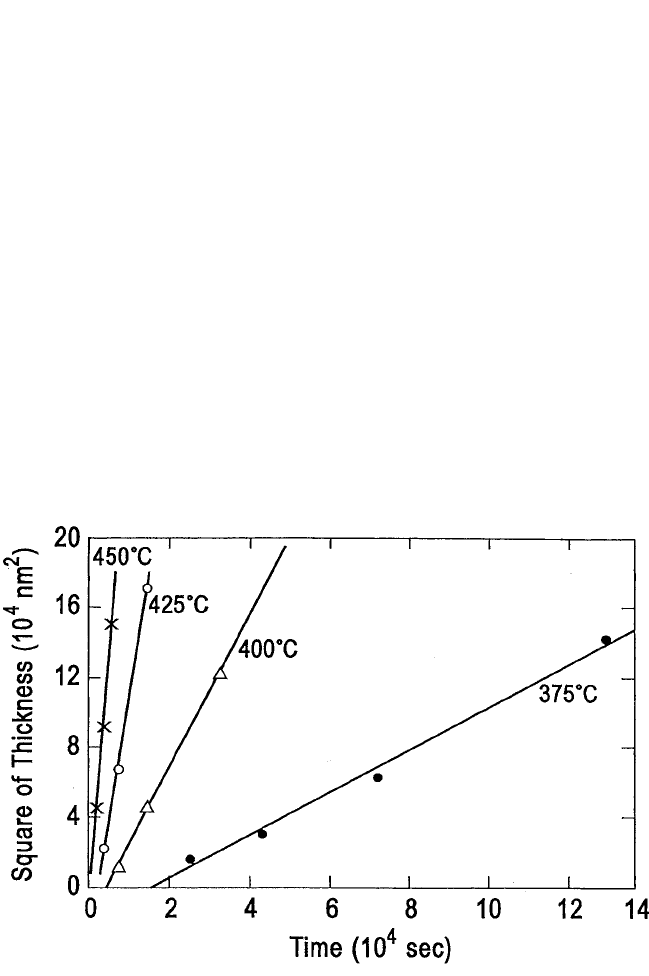
One problem with diffusion kinetics is that for thin layers, the kinetic

rates tend toward infinity, which is a physical impossibility. With thin

metal films reacting with silicon substrate, experimentally determined

kinetics follow the pattern in Fig. 6.3. Aplot of the square of the thickness

versus the time

[11]

is correct for the growth of Ru

, the only silicide

observed to grow in the reaction Ru-Si from a thickness of Ru smaller

than 100 nm. The data points for the diffusion-controlled growth do not

extrapolate to the origin. What occurs during the initial, so-called incuba-

tion period is often not known; when known, it tends to vary with the

mode of preparation of the samples (for example, deposition via evapora-

tion or sputtering). For the phenomenological description of interest here,

the details do not matter greatly. It is sufficient to state that initially, the

layer grows as a function of t

, where in order to have a finite rate of

Figure 6.3 Plot of the growth of Ru

, correctly done as thickness squared ver-

sus time. Note the positive time interception near the origin of the horizontal axis.

This corresponds to a period when overall growth proceeds as t

, with n equal to

or greater than 1. Unless precise information is obtained during that initial period,

we cannot know whether it corresponds to rate limitation from interface reaction.

From Petersson et al.

[11]

Ch_06.qxd 11/12/04 4:05 PM Page 290

REACTIVE PHASE FORMATION, D’HEURLE ET AL. 291

growth dLdt for t close to zero, n must be greater or equal to 1. In the

absence of either precise information or a proper description of the kinet-

ics during this initial period, it is simpler to take n equal to 1. As will be

shown in Sec. 6.2.4, this leads to linear-parabolic kinetics. In cases not so

well-known or defined, when n is indeed equal to 1, the initial growth

kinetics would be dictated by the rate of reaction. By reference to Eq. (4),

the growth law is then expressed as:

dLdt  a  [1  (L  aK)]. (14)

If L is large with respect to aK, Eq. (14) becomes identical to Eq. (4); if

L is small, the rate becomes equal to K. This latter parameter is referred

to as the reaction rate constant. It is indeed meaningful when the initial

stage of growth is limited by such an interface reaction. However, as

understood here, it should be taken more as a phenomenological constant

that provides a justifiable account of what happens at the beginning of a

phase formation when the rate cannot be infinite, so that experimental

observations can be plotted as in Fig. 6.3. The quantity aK has the

dimension of length, so that commentaries about Eq. (14) include state-

ments to the effect that this equation corresponds to two growth stages:

the first with linear growth, until a thickness aK, and a second stage with

parabolic kinetics. Such statements are erroneous, on L and t coordinates.

Eq. (14) defines a parabolic curve with a shift of origin so that at time

zero, dLdt assumes a finite value, K; there is no discontinuity at L 

aK.

[12]

Nevertheless, Eq. (14) leads to what is known as linear-parabolic

kinetics, often expressed as in the well-known formula for the growth of

silicon oxide:

[13]

 AL  Bt, (15)

where AB  1K and B  2a. When K has a physical meaning, in solid

state reactions, we may think of it as referring to diffusion across an interface,

somewhat akin to the situation during recrystallization, with relaxed phase

growth driven by the difference in free energy between the two regions. Then

diffusion across an interface of constant thickness is also constant, hence the

finite value of K. But in this sense, it is some sort of diffusion constant and

does not have the precise chemical meaning that an interface reaction rate

implies. Things are different when one of the reactants is a gas, for example,

oxygen during oxidation. Then one of the components of K is the rate of dis-

sociation of the molecular gas, from O

to atomic oxygen, that is necessary to

incorporate oxygen in a solid oxide (or H

and hydrides, and so forth).

[14]

It is paradoxical that the kinetics of oxide growth, which are often

identified with the thermal oxidation of Si,

[13]

and should therefore be

Ch_06.qxd 11/12/04 4:05 PM Page 291