Gubbins D., Herrero-Bervera E. Encyclopedia of Geomagnetism and Paleomagnetism

Подождите немного. Документ загружается.

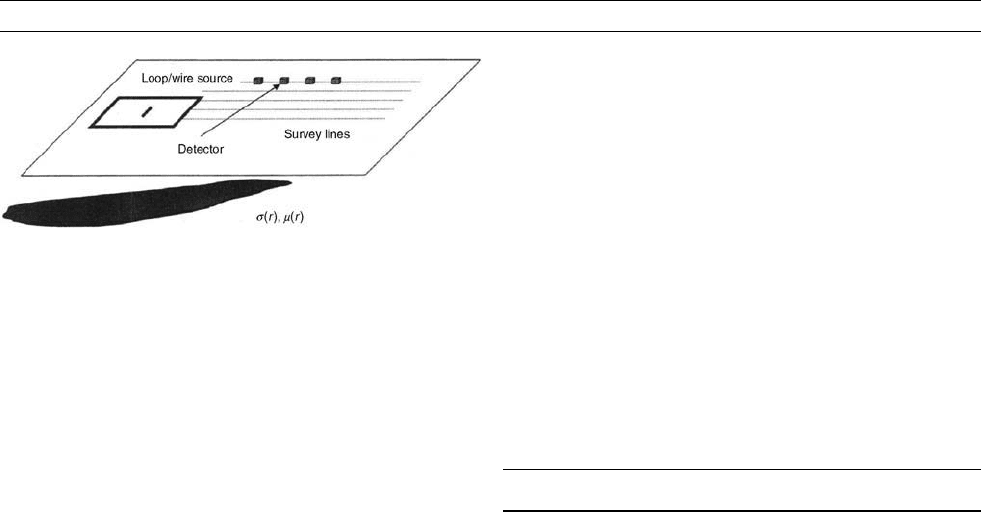
primary field is switched off and measurements made. The rapid

termination of the primary field in the TX causes Eddy current s to

be produced in the subsurface, and the associated secondary field is

measured on the surface using a detector (RX) coil (Figure T10). RX

may be a small multiturn coil (about 1m diameter) or a relatively large

loop. The decaying transient signal is sampled at various time gates to

yield a sounding curve. The transient signal can last from a few micro-

seconds to several hundreds of millisecond, and an observational

bandwidth of about 0.005–30 ms is desirable for near-surface investi-

gations (10–400 m). The character of the transient signal is a function

of the subsurface resistivity structure, with the shallow structure influ-

encing the TEM response at early times soon after TX turn-off and

measurement at increasing times allowing the deeper electrical struc-

ture to be interpreted. For shallow structure, TEM systems use high

base-frequencies (i.e., pulse repetition rates), small transmitter loops

(5–50 m), need only low power source (12 V battery), but in particular

requires a very rapid primary field turn-off (currently 1.5 ms). The

accuracy of the narrow early sampling times is also an important fac-

tor. For deeper structure, larger transmitter loops, higher power and of

course longer transient measuring times at the receiver are required.

There are a number of different configurations as regards the posi-

tion of the receiver relative to the transmitter (Figure T10). The recei-

ver can be located in the center of the TX loop (in-loop or central-loop

technique) or outside it (separated-loop or offset-loop arrangements).

In the single-loop or coincident-loop configuration, the TX loop serves

as the RX during transmitter-off times or both the TX and RX loops

are separate but coincident.

Maxwell A. Meju and Mark E. Everett

Bibliography

Arms, R.J., and Hama, F.R., 1965. Localized-induction concept on a

curved vortex and motion of an elliptic vortex ring. Physics of

Fluids, 8: 553–559.

Everett, M.E., and Meju, M.A., 2005. Near-surface controlled-source

electromagnetic induction: background and recent advance. In

Yoram, R., and Hubbard, S. (eds.), Hydrogeophysics. Heidelberg:

Springer (Chap. 6).

Hohmann, G.W., 1987. Numerical modeling for electromagnetic meth-

ods of geophysics. In Nabighian, M.N. (ed.), Electromagnetic

Methods in Applied Geophysics, Volume 1. Tulsa Oklahoma:

Society of Exploration Geophysics, pp. 313–363.

Jackson, J.D., 1998. Classical Electrodynamics, 3rd Edition. New

York: John Wiley & Sons, 808 pp.

Knight, J.H., and Raiche, A.P., 1982. Transient electromagnetic calcu-

lations using the Gaver-Stehfest inverse Laplace transform method.

Geophysics, 47:47–50.

Lamb, H., 1945. Hydrodynamics, by Sir Horace Lamb, 6th Edition.

New York: Dover Publications, 738 pp.

Meju, M.A., 2002. Geoelectromagnetic exploration for natural

resources: models, case studies and challenges. Surveys of Geophy-

sics, 23: 133–205.

Meju, M.A., Fenning, P.J., and Hawkins, T.R.W., 2000. Evaluation of

small-loop transient electromagnetic soundings to locate the Sher-

wood Sandstone aquifer and confining formations at well sites in

the Vale of York. England Journal of Applied Geophysics, 44:

217–236.

Nabighian, M.N., 1979. Quasi-static transient response of a conduc-

ting half-space: an approximate representation. Geophysics, 44:

1700–1705.

Raiche, A.P., 1984. The effect of ramp function turn-off on the TEM

response of layered earth. Exploration Geophysics, 15:37–41.

Taylor, G.I., 1958. On the dissipation of eddies. In Batchelor, G.K. (ed.)

Scientific Papers, Volume 2. Cambridge: Cambridge University

Press, pp. 96–101.

Wangsness, R.K., 1986. Electromagnetic Fields, 2nd Edition. New

York: John Wiley & Sons, 608 pp.

TRUE POLAR WANDER

Definitions and early views

The idea that polar wander (PW) must have occurred dates back to the

19th century. Geologists, paleontologists, and paleoclimatologists

suggested that the Earth’s equator must have been located far from

its present position in the distant geological past, at least viewed from

certain continents, given the present day locations of climatological

belts derived from certain types of rocks or fossil assemblages. Darwin

(1877) made the first attempt at quantitative modeling but this suffered

from several errors (see Steinberger and O’Connell, 2002, for an

analysis). In the early 1950s, paleomagnetists provided quantitative

evidence that the geographical latitudes of individual continents had

indeed changed with time, hence that the instantaneous geographic

or rotation pole had moved with respect to most continents. The paths

followed by the poles in the geological past were termed “apparent”

polar wander paths (or APWPs), because it was not clear whether it

was the pole or the continent that had moved. It would soon become

apparent that continents (more accurately tectonic plates) had moved

with respect to each other and that a significant part of APW was actu-

ally due to these relative motions. The question was: is there a remain-

ing fraction in polar wander, which would be a characteristic of “Earth

as a whole,” and which would not be accounted for by plate tectonics.

This fraction is what is generally called “true” polar wander (TPW).

TPW refers to the large scale motions of the Earth’s rotation axis

with respect to the “bulk silicate Earth” or “solid Earth” through geo-

logical time (rather than “Earth as a whole,” indeed, much of the core

is a fluid with small viscosity and the parts which will be important to

us in this article are the solid though slowly deforming mantle and

crust, i.e., the silicate earth; see below). External forces driving shorter-

term changes, such as precession, are not considered here. TPW could

result from centrifugal forces acting on mass anomalies distributed on

or inside the Earth: excess mass, for instance, will lead to slow defor-

mation of the Earth and change its rotation axis, causing the mass to

move towards the equator without being displaced with respect to

the solid Earth. The problem is to define precisely which part wanders

with respect to which reference frame in a deformable Earth. We seek

to identify the axis of rotation of a reference frame RF which is rele-

vant to the solid Earth relative to an inertial (or absolute astronomical)

frame of reference IFR (i.e., determined by the angular momentum

vector of Earth; see f.i. Steinberger and O’Connell, 2002). The refer-

ence frame RF can be selected as the one which has zero net rotation

when motions are integrated over the entire mantle, called the “mean

mantle” reference frame. Or one can define a “mean lithosphere”

frame, in which the lithospheric plates have no net rotation. Because

Figure T10 Basic set-up for TEM surveying. The ground is

inductively energized using a grounded wire or transmitter loop.

The electric or magnetic fields induced in a subsurface conductor

(s(r)) are systematically measured along survey lines using a

suitable detector coil.

956 TRUE POLAR WANDER

of lateral variations in viscosity of the deformable Earth layers, these

frames in general do not coincide (Ricard et al., 1991; O’Connell

et al., 1991). Although the “mean mantle ” frame can be computed

in numerical simulations in which the density distribution is given in

the entire mantle, when attempting to constrain it with actual (paleomag-

netic) observations, we will have to assume that the “mean mantle”

frame is identical to some frame based on observations: the “hotspot

reference frame” will most often be the one involved. Steinberger

and O’Connell (2000) calculate that the approximation is good even

if hotspots move in the convecting mantle (see also Davies, 1988;

Steinberger, 2000). This is discussed further later in this article.

Is the concept of Earth as a whole meaningful? If the Earth were per-

fectly rigid, there would be no polar wander. Of course we now know that

the Earth is not rigid, and that its crust and mantle actually deform

actively at the typical velocities of plate tectonics (10–100 mm yr

1

Thus, PW involves (relative) motions of the rotation axis with respect

to the Earth’s mantle. Lambeck (1980) points out that from the time of

Kelvin, in 1863, up to the work published by Gold in 1955, a number

of qualified physicists believed that polar wander was not only possible,

but even inevitable if the long-term rheology of the planet was inelastic.

However, in a landmark treatise on the rotation of the Earth, Munk

and Macdonald (1960) were led to question both the observational and

theoretical bases for large-scale polar wandering. They considered that

evidence from either paleomagnetism or paleontology available at that

time was at best tenuous, and proposed that the “excess” bulge (the

present bulge is indeed larger than what would be expected if the Earth

behaved as a fluid, called the hydrostatic bulge) was a fossil remainder

from a time when the Earth rotated faster.

A decade later, plate tectonics and continental drift had basically

been established. Another landmark paper by Goldreich and Toomre

(1969) reflected the new view of the Earth. They hypothesized that

(large scale) polar wandering and continental drift shared a common

explanation through mantle convection and resulting redistribution of

masses within the mantle. Goldreich and Toomre (1969) started their

analysis of the motions of the rotation axis of a quasirigid (slowly

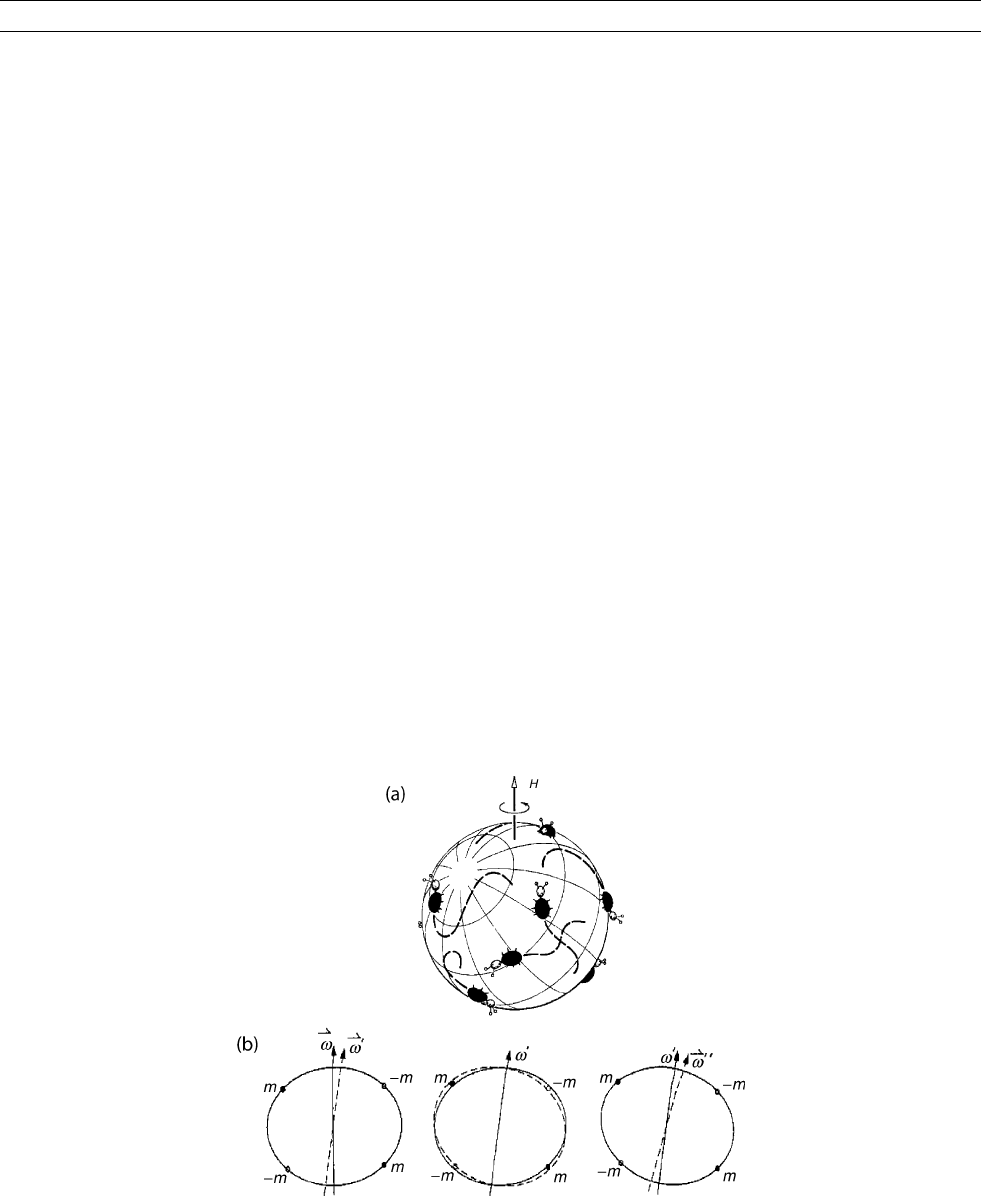
deforming) Earth with the now classical figure (inspired by Gold,

1955) where a colony of beetles (the continents or other mass anomalies)

move slowly at the surface of a rigid rotating sphere (Figure T11a). They

used this to demonstrate that, once set spinning about the axis with the

greatest nonhydrostatic moment of inertia, a slowly deforming body

would always continue to spin almost exactly about the same principal

axis, as that axis moved through it. Viewed from space, the rotation

and principal axes are fixed with respect to the stars, and the crust

and mantle move relative to it (again, the shorter-term effects of

precession are neglected here). The speed of motion is N

1/2

times

the average speed of the N beetles of mass m; hence if N (and m)is

large, large polar wandering is possible. In a numerical experiment,

Goldreich and Toomre (1969) simulated very large polar wander, with

particularly intense and rapid swings.

The physics of TPW can be explained in a (hopefully) simple way

(e.g., Ricard et al., 1993a; Steinberger and O’Connell, 2002). TPW

is seen as the result of conservation of angular momentum of a rotat-

ing, deformable body (i.e., whose inertia tensor slowly changes with

time). In simple terms, the inertia tensor comprises three components

(1) the inertia of a spherical Earth, (2) the hydrostatic equilibrium

part, that is the inertia of its equatorial bulge (which, as mentioned

above, is slightly larger than what it would be if the planet were a

fluid), and (3) the remainder, the “total” nonhydrostatic contribution

to the inertia tensor, which itself comprises a contribution “imposed”

by mantle convection (linked to subducting slabs, upwell ing plumes,

and more generally thermal and chemical mass heterogeneities result-

ing from the long history of mantle convection) and one caused by the

change of the rotation axis and the immediate elastic and delayed

viscoelastic adjustment to the new equilibrium shape. Each of the three

terms is very small compared to the previous one. Changing the rota-

tion of a spherical object (term 1) does not require energy on geologi-

cal time scales; the bulge (term 2), itself a function of rotation, results

in a viscous drag which controls only the speed at which rotation can

Figure T11 (a) Diagram illustrating polar wander on a quasirigid planet (after Goldreich and Toomre, 1969; Gordon, 1987). The beetles

represent mass anomalies which change with time (drifting plates or mantle heterogeneities), inducing changes in the principal

nonhydrostatic moments of inertia. The coordinate system attached to the (slowly deforming) solid planet moves with respect to the

rotation (or spin) axis. (b) Example of interplay between deformation and change of the rotation axis of the Earth in the hypothetical

case when four mass changes (two positive or excess, two negative or deficit) are imposed such that the center of mass does not change

and only one nondiagonal inertia tensor element changes (from Steinberger and O’Connell, 2002). In an absolute astronomical

reference frame the direction of the rotation axis is fixed; positive masses drift to the equator (and negative ones away). Therefore the

relative position of the rotation axis changes with respect to the mass distribution, the change in rotation axis causes the Earth to

deform, the change in shape causes the axis to move further, until a new equilibrium is asymptotically approached.

TRUE POLAR WANDER 957

change; as a result, the direction of rotation is fixed by the smallest

term (term 3), i.e., the nonhydrostatic component. The rotation axis

tracks the maximum eigenvector of the nonhydrostatic inertia tensor

as fast as adjustment of the hydrostatic bulge allows (Figure T11b

illustrates this for a simple case): the hydrostatic bulge is a response

to the current rotation axis, and it will move in accord with the motion

of that rotation axis, which is determined by the nonhydrostatic inertia

tensor. Seen from an observation point on the surface of the Earth,

TPW appears as the wave-like propagation of the bulge. Ultimately,

the viscosity of the mantle will control the rate of this motion (Ricard

et al., 1993a,b; for a recent synthesis and numerical results showing

the time scales involved, see Steinberger and O’Connell, 2002).

With estimates of degree 2 components of the geopotential derived

from satellite data, Goldreich and Toomre (1969) showed that the non-

hydrostatic part of the earth’s inertia ellipsoid is triaxial, the present

rotation axis coinciding with the largest of the nonhydrostatic

moments of inertia. Therefore, there was no need to resort to the idea

of a fossil bulge: the nonhydrostatic Earth simply departs from perfect

sphericity. Goldreich and Toomre’s (1969) Earth had no bulge to con-

trol the rotation speed (on a rotating planet, the faster the beetles the

more random their paths and the less the viscous bulge has time to

flow, impeding TPW); also isostatic compensation implies that only

objects far from interfaces (such as subductions and upwellings, not

surface plates or beetles...) which are not isostatically compensated

can act (e.g., Ricard et al., 1993b). But their presentation had a goal

of pedagogical efficiency and in that sense was quite successful.

How is TPW measured (on short time scales)?

Now, how can we obtain measures of the position of the rotation axis

of the Earth? This depends on the time scale. On the short side of the

scale, astronomers and geodesists are the appropriate experts. Accord-

ing to these scientists, polar wandering is occurring at present. One of

the most recent determinations uses the star catalogue established from

the Hipparcos astrometric satellite (determinations of the positions,

proper motions, and parallaxes of 100000 stars). Optical astrometric

measurements of star positions made during the past century have

been rereduced using that catalogue by Gross and Vondrak (1999),

producing the longest available homogeneous series of polar motion.

The annual, Chandler, and Markowitz wobbles (all periodic or quasi-

periodic with annual to decadal periods) have been separated from

the longer-term trend of the mean pole (which is of interest to us).

The result (see arrow in Figure T12) is a mean drift of the Earth’s

rotation pole over the period 1900–1 992 of 3.5 milliarcs ec yr

1

(or

107 mm a

1

or 107 km Ma

1

for later comparison with geological

values), along the direction of the 79



W meridian (uncertainties on

absolute values are a few per mil). Data reduction involves modeling

of tectonic plate motions, tidal variations and ocean loading and this

estimate of present-day TPW is considered as the best unbiased one.

This is actually not far from earlier determinations, for instance by

Markowitz (1970) (3.5 milliarcsec yr

1

towards 65



W longitude).

It has been proposed since the late 1970s that this long-term polar

wander is largely due to postglacial rebound, i.e., lithospheric and

mantle response to melting of ice (e.g., Sabadini and Peltier, 1981;

Mitrovica and Milne, 1998), which has mainly a vertical expression

at the surface. The pole is moving toward Hudson Bay, where a large

ice mass melted and the lithosphere is currently rising. Possibly contri-

buting sources include mantle convection (Steinberger and O’Connell,

1997), and secular change in ice sheet mass and sea-level (e.g., James

and Ivins, 1997). McCarthy and Luzum (1996) compare theoretical

estimates and conclude that snow loading, changes in Antarctic ice

and Pleistocene deglaciation all provide estimates in reasonable agree-

ment with observations. Melting of glaciers or changes in major

hydrological reservoirs are at least a factor of 10 less efficient. Overall,

the hydrostatic bulge adjusts to changes in the position of the Earth ’s

rotation axis in about 10

years, which is the characteristic time for

upper mantle deformation (glacio-isostatic rebound).

How is TPW measured (long time scales)?

How long have the recent rate and direction been maintained, and

what values applied in the geological past? On these longer time

scales, say longer than 10

years, paleomagnetism has become the

primary source of information. Although interesting information comes

from geological field observations (reconstruction of paleoclimate

belts based on occurrences of fossils or certain rock types, or wind

Figure T12 (a) True polar wander paths deduced from the hotspot model of Mu

ller et al. (1993) going from the Present back to

130 Ma, and that of Morgan (1983) going from 130 back to 200Ma, with associated 95% confidence ellipses (shaded light gray);

20 Ma sliding window. Ages are in Ma and correspond to the actual mean age of the data in the corresponding window, which

is why they are not regularly distributed when the original time windows were. Note that the external circle is at 50



latitude.

(b) A simplified outline of the TPW path of (a) outlining successive episodes and standstills. The long arrow shows the mean direction

of pole motion between 1900 and 1990 (79



W with a large uncertainty); modulus is 107 mm a (see text, section “How is TPW

measured (on short time scales)?”). (After Besse and Courtillot, 2002).

958 TRUE POLAR WANDER

directions), the key source of quantitative information on polar wander

originated from the first paleomagnetic works in the 1950s (with the

seminal paper of Creer et al., 1954), and paleomagnetism has remained

the main provider of such data. Although clearly doubtful, Munk and

MacDonald (1960) already spent a first long chapter on paleomagnetic

evidence of polar wander, noting the importance of early syntheses by

Runcorn (1956) and several others who demonstrated that continents

could not have remained in the same relative positions throughout

geological time. A recent review of paleomagnetism is given by

McElhinny and McFadden (2000).

The apparent polar wander paths from all the major plates are being

defined with increasing accuracy, and their differences reflect conti-

nental drift and plate tectonics. This demonstration of the reality of

“apparent” polar wander seen from any plate has led some to propose

that the concept of “true” polar wandering might be irrelevant or

unnecessary (see review in Gordon, 1987). McKenzie (1972) noted

that the concept of PW could be useful if the motion of the pole rela-

tive to any one plate was much larger than the motion between pairs of

plates (Figure T13). The most often accepted view is that the concept

is worthwhile if a reference frame external to the plates themselves can

be defined, in which there was significant motion of the pole. Various

attempts, namely the “vector-sum” and “mean-lithosphere frame”

methods, have been reviewed for instance by Jurdy (1981) and Gordon

(1987). The “mean-lithosphere frame,” first proposed by Jurdy and

Van der Voo (1974, 1975), minimizes the difference between a displa-

cement (vector) field and a rigid rotation of the entire Earth’s surface.

Jurdy and Van der Voo found no significant change in the Cenozoic

and Jurdy (1981) concluded in favor of hotspot motion, not TPW.

Hargraves and Duncan (1973) had earlier proposed the idea of “mantle

roll” in which the nonlithospheric mantle “rolls” beneath the mean

lithosphere to which the rotation axis is fixed. McElhinny and McFadden

(2000, p. 328) repeated some of these calculations with updated

kinematic and paleomagnetic data and concluded that TPW was not

discernible from zero over the past 50 myr, as had been found by Jurdy

and Van der Voo (1974, 1975).

However, most studies performed in the last two decades follow an

alternate approach, based on the possibility, originally suggested by

Morgan (1972, 1981), that hotspots could provide a valid refer-

ence frame for the mantle. The meaning and existence of that reference

frame has been the subject of continued debate, up to this day.

Apparent and TPW, and the hotspot reference frame

We recall that hotspots are active volcanoes, apparently unrelated to

(and often but not always far from) plate boundaries, which have been

active for tens of millions of years. Hotspots are supposed to be the

surface manifestation of plumes, which have left traces in the form

of (quasi-) linear chains of extinct volcanoes on the plate(s), which

passed over them. Morgan (1972, 1981) proposed that these plumes

have a “deep” mantle origin: these convective instabilities may be

anchored at least down to the transition zone and possibly all the

way down to the core-mantle boundary (yet another topic of heated

debate). As a plate moves over such a plume, the relative motion

can be described by a rotation about a pole, which is often called the

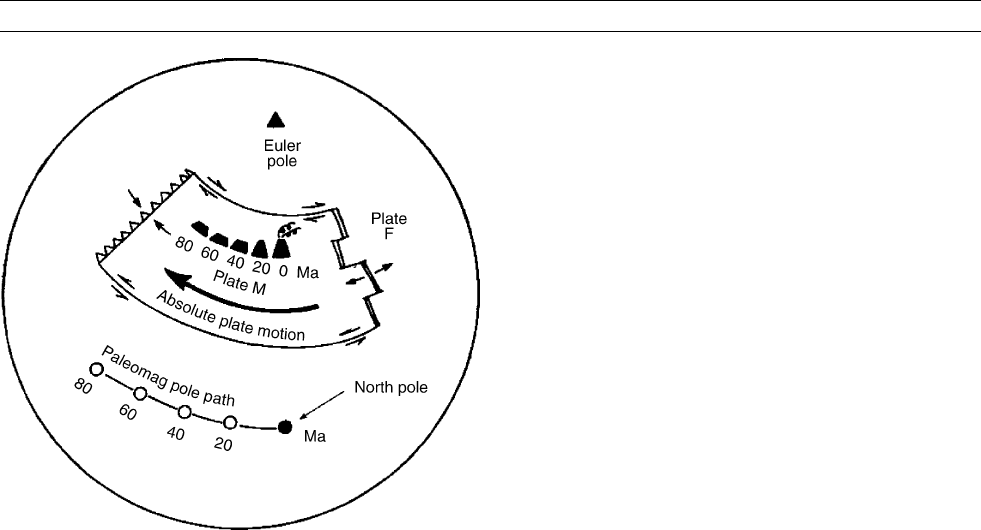
Euler pole: if the rotation axis remains unchanged, the trace of the

plume (the hotspot track) will form a small circle about the Euler pole,

as do transform faults about the relative rotation axis of two plates

(Figure T14). If the traces can be identified and the extinct volcanoes

dated, one can define a “hotspot apparent polar wander” (Gordon,

1987) in the same way one defines the apparent polar wander path

of any plate. If hotspots are indeed fixed with respect to each other

and are fixed within the mantle (we will return to these essential

assumptions), then hotspot apparent polar wander describes the

wander of the Earth’s rotation axis with respect to the hotpots (or vice

versa). It is this motion of the pole with respect to the hotspots,

assumed to act as a reference frame for the mantle, which has been

taken as an estimate of TPW. Motion of plates with respect to the hot-

spots is sometimes (improperly) called “absolute motion.” Note that

“APW” (corresponding to a rotation operator O

), i.e., the rotation of

the Earth’s rotation axis with respect to a given plate, “HS” or “absolute

motion” (corresponding to a rotation operator O

), i.e., the rotation of the

plate with respect to the hotspot reference frame, and “TPW” (corre-

sponding to a rotation operator O

), i.e., the rotation of the Earth’ s rota-

tion axis with respect to the hotspot reference frame are linked through

the simple equation: O

¼O

O

(i.e., as soon as two of them are given

the third can be derived, see, e.g., Besse and Courtillot, 2002).

Determining TPW in that sense requires the best possible knowl-

edge of APWPs of all plates (i.e., the best possible data base of paleo-

magnetic poles to determine the paleolatitudes and orientations of

plates with respect to the rotation axis), of their relative motions (e.g.,

kinematics from oceanic data such as marine magnetic anomalies and

azimuths of transform faults), and positions and ages of individual volca-

noes along hotspot tracks on as many plates and for as many hotspots as

possible. Paleolatitudes of these seamounts are used for comparison to

test model predictions. Note that (except in the final part of this article)

we will restrict ourselves to the last 200 million years (i.e., the time for

which some ocean kinematic information is preserved).

APWPs and kinematic models were developed from the 1960s to the

1980s under the key assumption that, when averaged over a sufficient

amount of time, in excess of a few thousand years, the Earth’s magnetic

field could be described accurately by a geocentric axial dipole

(so-called GAD hypothesis). Following early attempts by Livermore

et al. (1984) and Andrews (1985), Besse and Courtillot (1988, 1991)

proposed to blend the two data sets (i.e., the paleomagnetic poles used

Figure T13 True polar wander in the mean lithosphere reference frame. Each thin solid line with arrow represents motion of the

north pole (NP)

with respect to a plate n (or vice versa). The thick vector V

links NP with the center of gravity of the end-points

of all individual velocity vectors (weighed by the fractional area occupied by each plate). True polar wander is considered useful

when the modulus (scalar magnitude) of V

is large compared to those of the dashed vectors representing velocities with respect to

the center of gravity,

–V

. (after McKenzie, 1972; McElhinny and McFadden, 2000).

TRUE POLAR WANDER 959

to derive the APWPs and the oceanic data used to derive plate kinematic

models). They used then available paleomagnetic data (from North

America, Africa, Eurasia and India) and kinematic models (from the

Indian, Central Atlantic, and North Atlantic oceans) and produced a

“synthetic” APWP, which was defined with respect to South Africa

and then transferred to all other plates. Motion of hotspots with respect

to the plates was then integrated to derive an estimate of TPW. As a con-

sequence of publication of a Global Paleomagnetic computerized Data-

base and of much improved reconstructions of past plate motions, this

work was updated recently (Besse and Courtillot, 2002).

A recent TPW curve for the last 200 million years

The resulting TPW curve, based on 242 independent data from the

African, Antarctic, Australian, European, Greenland, Indian, and

North and South American plates, is shown in Figure T12a with a

20 myr time resolution. Points are shown with their 95% confidence

circles (radii A

) every 10 myr and every other point is statistically

independent (estimates at 5 myr intervals are also available in that

study). We recall that the 95% confidence intervals depend on many

parameters linked to paleomagnetic data collection and laboratory

treatment (see, e.g., McElhinny and McFadden, 2000, p. 91), but fail

to explicitly include uncertainties on plate motions: they are supposed

to be our best estimate of the cone within which the “true” direction is

expected to lie. In other terms, there is a remaining 5% chance that our

determination is more than A

away from the true direction.

The first points, corresponding to the period 8–59 Ma, are all in the

same quadrant, between 3.3



and 5.9



away from the present rotation

pole, with 95% uncertainties ranging from 2.0



to 3.8



. They are not

statistically distinct from each other and therefore could correspond

to a standstill. A mean position can be calculated from all (102) data

points in that time window: it is found to lie at 85.1



N, 153.3



¼ 1.5



), significantly displaced from the pole. The youngest mean

pole at 5 Ma (mean age 3.0  2.4 Ma) is at 86.4



N, 166.8



¼ 2.5



), also significantly displaced from the pole but not statis-

tically different from the 8–59 Ma overall mean. It seems that TPW

may have been negligible for an extended period of about 50 myr,

but accelerated a few myr ago, with a velocity on the order of

100 km myr

1

. The path displays a succession of a standstill at

160–130 Ma, a quasicircular track from 130 to 70 Ma, then the

standstill at 50–10 Ma and the faster motion up to the present

(Figure T12b). The TPW rate between 130 and 70 Ma averages

30 km my

1

. This would confirm earlier findings (e.g., Andrews,

1985; Besse and Courtillot, 1991) that TPW appears episodic in nature,

with periods of (quasi-) standstill alternating with periods of faster TPW.

The typical duration of these standstill periods is on the order of a few

tens of millions of years (50 myr). Because of all the uncertainties in

models of hotspot kinematics prior to 130 Ma, it is not safe to place

too much weight on behavior prior to that time. The major event since

then is therefore the end of the 130–60 Ma period of relatively fast polar

wander, with the standstill (i.e., no or little TPW) from 60 Ma (actually

because of larger 95% confidence circles, possibly 80 Ma) to 10 Ma.

Marcano et al. (1999) find TPW rates on the order of or less than

40 km myr

1

in the Permotriassic, i.e., typical of times since then,

extending the period of moderate TPW back to more than 250 myr.

However uncertain, evidence for the fact that Earth emerged from a

long standstill to enter a new period of faster polar wander in a differ-

ent direction 10 Ma ago (5 Ma at the higher resolution) is particu-

larly interesting. That period would then still be going on. The

youngest pole at 5 Ma, taken at face value, would imply a TPW rate

of 130 km myr

1

in the direction 15



W (with a large azimuthal

uncertainty from 10



Eto40



W, due to proximity of the 5 Ma pole

to the present rotation axis). The first-order agreement with recent

astronomical determinations (107 km myr

1

in the direction 79



with a possible range from 65



Wto85



W; see section “How is

TPW measured (on short time scales)?”) has reinforced the idea that

this might be a valid estimate and that TPW might have been rather

uniform over the last few millions of years, corresponding to signifi-

cant, large scale changes in ice cover. Ice is not considered to have

played a significant role before, and it was absent prior to 30 Ma.

Does super fast TPW occur?

Prévot et al. (2000) argue for an episode of super fast TPW between

114 and 118 Ma (in excess of 500 km myr

1

). Besse and Courtillot

(2002; see also Cottrell and Tarduno (2000), and Tarduno and Smirnov,

2001, 2002) critically discuss this and other suggestions at other

epochs (e.g., Petronotis and Gordon (1999) at 80–70 Ma; Sager and

Koppers (2000) at about 84 Ma). They conclude that none of the

several suggested super fast events (with velocities of hundreds of

km myr

1

) is based on sufficiently robust sets of observations. For

instance, Cottrell and Tarduno (2000) tested the hypothesis of Sager

and Koppers (2000) using data from Italian sections and found that

it failed the test. On the other hand, Besse and Courtillot (2002) and

Tarduno and Smirnov (2002) showed that the episode found by Prévot

et al. (2000; see also Camps et al., 2002) was not statistically robust

due to the use of too short time windows. Gordon et al. (2004)

recently conclude in favor of a super fast episode seen on the Pacific

plate between 88 and 81 Ma (see below). However, it remains reason-

able (in the author’s view) to assume that many of these features

correspond to erroneous individual data or other sources of error. Only

the recent phase of TPW since 5 Ma may prompt us to accept that

TPW velocities up to 100 km myr

1

can be maintained over periods

of millions of years (Figure T12).

Two of the nagging questions which must be fully addressed before

the concept of global TPW and the velocities mentioned above can be

accepted are geometry of the mean geomagnetic field and hotspot fixity.

Figure T14 Relationship between hotspot tracks and segments of

APW paths if the spin axis has been fixed with respect to the

hotspots. Plate F is fixed relative to the hotspots, while plate M

rotates about the Euler pole relative to plate F, the hotspots

and the paleomagnetic axis (assumed to coincide with the spin

axis). The hotspot trace on plate M, the transform faults on the

plate boundaries between F and M, and the segment of the

APW path all lie on small circles centered on the Euler pole

(Gordon, 1987).

960 TRUE POLAR WANDER

Is the mean field sufficiently close to an axial dipole?

Slight departures from a purely centered ancient dipole field have

been noted as early as 1970, when Wilson argued for a far-sided and

right-handed distribution of virtual geomagnetic poles during the

Cenozoic: average paleomagnetic poles tend to fall beyond the geogra-

phical pole and to the east of it, seen from the site where the data have

been obtained. A number of analyses concluded that, when averaged

over the last few million years, an axial quadrupole component

is detectable, with an amplitude on the order of 3–6% of the axial

dipole (e.g., Constable and Parker, 1988; Schneider and Kent, 1990b;

Quidelleur et al., 1994; Carlut and Courtillot, 1998). Livermore et al.

(1983, 1984) tried to extract such a quadrupolar term in a worldwide

paleomagnetic database going back 200 myr

1

. More recently, Besse

and Courtillot (2002) find moderately far-sided poles, consistent with

a persistent quadrupole moment (on the order of 3  2% of the dipole

over the last 200 myr), but its amplitude can be neglected for many

applications. The GAD hypothesis has recently been further chal-

lenged by suggestions that significant long-term octupolar contribu-

tions of between 6 and 25% of the GAD may have existed for

Precambrian through early Tertiary time (Kent and Smethurst, 1998;

Van der Voo and Torsvik, 2001; Si and Van der Voo, 2001; Torsvik

et al., 2002). For instance, Si and Van der Voo (2001) propose that a

value of 6% would account for the low inclinations observed in central

Asia in the Cretaceous and early Tertiary. A symposium in honor of

Neil Opdyke has reviewed the pros and cons of octupolar contributions

to the long-term mean field (the reader is referred to the corresponding

AGU monograph and to other articles in this encyclopedia). Courtillot

and Besse (2004) attempt to find evidence for octupolar contributions

in the 0–200 myr period. In that new analysis, data from sites believed

to have possibly undergone a tectonic rotation about a local vertical

axis are included, contributing 174 out of 465 data. The positions of

mean poles are analyzed in 20 myr windows in common-site longi-

tude, respectively, for the northern mid-latitudes, equatorial and south-

ern mid-latitudes, searching for the distinctive antisymmetrical pattern

expected for a dipole plus octupole field. They next analyze the distri-

bution of “latitude anomaly” (derived from the inclination anomaly,

i.e., observed minus expected in case of a pure dipole) versus dipole lati-

tude. Based on these various data manipulations, they find no robust

evidence for an octupole and estimate that values on the order of 5%

are unlikely to have been exceeded in the last 200 myr. A preliminary

200 myr overall mean field has an octupole of 3  8% (i.e., not signif-

icant; note that the present day value is on the order of 4%, but this is an

“instantaneous value” with large secular variation, which in large part

could average out). Thus field geometry is unlikely to severely alter

TPW estimates, for which it is not the main source of “noise.”

Is the estimate of TPW truly global?

A legitimate concern regarding the above conclusions is due to the fact

that the analysis is not truly global, in that it fails to encompass the

Pacific plate. Petronotis and Gordon (1999) have compiled an APW

path (nine poles from 125 to 26 Ma) for the Pacific plate, with four

poles based on the analysis of skewness of ocean crust magnetic

anomalies, three on seamount magnetic anomaly modeling (Sager

and Pringle, 1988) and two undetermined. Using the Pacific plate

versus hotspot kinematic model of Engebretson et al. (1985), based

on dating of volcanoes which are part of hotspot tracks such as

Hawaii, Louisville, or MacDonald (see, e.g., Figure T15 in the case

of Hawaii), Besse and Courtillot (2002) have determined a correspond-

ing 125–26 Ma “Pacific hotspot only” TPW curve. The “Pacific” and

“Indo-Atlantic” TPW curves are compared in Figure T16. This com-

parison is interesting because the data sets they are based on are

Figure T15 The Hawaii-Emperor seamount chain in the Pacific (ETOPO5 bathymetry image). The track with diamonds, which

closely follows the observed one, is for the best-fit Pacific plate motion. Two reconstructed tracks of Pacific-hotspot motion in the

Indo-Atlantic reference frame are also shown with quantitative plate reconstruction error ellipses. The reconstructed track, which is

closer to the observed one, includes East-West Antarctic motion. Chrons and ages (in Ma) are shown (after Raymond et al., 2000).

TRUE POLAR WANDER 961

entirely different and independent. Despite some significant differ-

ences to which we return shortly, it is worth emphasizing that the

two curves are altogether similar in shape (tracks, amplitudes,

azimuths), particularly the 300



longitude trending track from 130 to

70 Ma, though the two are offset (in the same general direction) by

about 7



. More precisely, the confidence intervals intersect (though

points are not in the intersection) near 125, 90, 60, 40 and 30 Ma.

The main differences occur between 80 and 70 Ma: the 82 and

65–72 poles derived from Petronotis and Gordon (1999) and the

77 and 67 Ma poles derived by Besse and Courtillot (2002) are clearly

distinct. In as yet unpublished work, Gordon et al. (2004 and

R. Gordon, personal communication March 2004) have updated the

APW path of the Pacific plate. It is now defined by 11 paleomagnetic

poles from nonoverlapping age windows going back to 125 Ma. Nine

of these poles (32–81 Ma) are determined from skewness analysis.

Comparing their APWP to Pacific hotspot motion with respect to the

spin axis, Gordon et al. (2004) find a TPW curve which agrees fairly

well with their previous analysis, except for a significant change in the

32–40 Ma pole. The new curve implies rather small motion between

81 and 32 Ma, with larger swings before and after. The most recent

shift, during the past 30 myr, is about 10



(or 35 km myr

1

on aver-

age). A bigger shift by about 20



would have occurred between

88 and 81 Ma (i.e., more than 300 km myr

1

, an episode of super fast

motion which in our view remains to be demonstrated). Comparing

the new Pacific TPW curve to the Indo-Atlantic one derived by Besse

and Courtillot (2002), Gordon et al. (2004) conclude that there is no

significant net motion between Pacific and Indo-Atlantic hotspots in

the past 125 myr

1

(see section “Are hotspots fixed with respect to each

other?”). This conclusion depends both on data quality and on the valid-

ity of the plate motion models.

There are ongoing debates on the validity of the data used by

Gordon and collaborators to construct their Pacific APWP, whether

the uncertainty regions they use are realistic, and also on the question

of fixity of Pacific hotspots with respect to each other and to the “Indo-

Atlantic” hotspots (see below). For instance, Tarduno and Cottrell

(1997; see also Tarduno et al., 2003) have determined the paleolatitude

(based on inclination-only data from cores) of the 81 Ma old Detroit

Seamount, which is part of the Emperor chain, not far from its

northern termination in the Kuril Trench. The paleolatitude (36.2 þ

6.9/7.2



) is distinct from that based on the 81 Ma pole of the Pacific

APWP (Sager and Pringle, 1988) which is on the order of 20



N, based

on seamount anomaly poles. Tarduno and Cottrell (1997) exclude the

possibilities of inadequate sampling of secular variation, bias due to

unremoved overprints or off-vertical drilling. They point out the uncer-

tainties encountered when building an APWP for an oceanic plate,

such as the Pacific, solely from inversions of magnetic surveys over

seamounts and/or analysis of skewness of marine magnetic profiles.

Following several authors (e.g., Parker, 1991), Di Venere and Kent

(1999) and Cottrell and Tarduno (2000) argue that the reliability of

the Pacific paleopoles based on either modeling of seamount magnetic

anomalies or determination of skewness of marine magnetic anomalies

should be considered suspect. Both are prone to numerous biases and

could yield errors in excess of 10



in the position of the mean poles

derived from them. Seamounts suffer from induced and viscous mag-

netizations, and potential unresolved multiple polarities of magnetiza-

tion. Skewness suffers from anomalous skewness as recognized by all

users of such data. If one uses only the highest resolution, standard

paleomagnetic data from the Pacific, much of Mesozoic TPW for that

plate is seen as motion between hotspot groups (e.g., Tarduno and

Gee, 1995).

Are hotspots fixed with respect to each other?

We must therefore now review briefly the question of hotspot fixity.

Norton (1995) has suggested that the famous 43 Ma Hawaiian bend

in the Hawaiian-Emperor hotspot track (see Figure T15) was actually

a “nonevent,” i.e., indicated a change in motion of the Hawaiian hot-

spot with respect to the mantle rather than a change in Pacific plate

motion. Koppers et al. (2001) have tested the fixed hotspot hypothesis

for Pacific seamount trails. They use seamount locations to first

determine stage Euler poles, which they then test against observed

Ar/

Ar age progressions. The main stages tested are 0–43, 43–80,

and 80–100 Ma. Koppers et al. find that the 0–43 Ma Hawaiian and

Foundation seamount trail pair is the only one compatible with the

fixed hotspot hypothesis. Most other trail pairs would require relative

motions of order (or in excess) of 10 km myr

1

. The 43–80 Ma

Emperor/Line pair shows particularly large discrepancies, requiring

motions of at least 30 km myr

1

. Based on careful analysis of 14 Pacific

seamount tracks, using updated age determinations and bathymetry,

Clouard and Bonneville (2001) show that Pacific seamounts are actually

created by different processes, many being short-lived. They conclude

that only the Hawaii and Louisville chains qualify as long-lived hotspots

that can robustly be tested for fixity.

Di Venere and Kent (1999) have addressed the problem of relative

motion between the Pacific and Indo-Atlantic groups of hotspots,

using paleomagnetic results from Marie Byrd Land in West Antarctica.

Though they demonstrate that some motion must have taken place

since 100 Ma between West (Marie Byrd Land) and East Antarctica,

they conclude that this motion cannot account for more than 20%,

and possibly as little as 4% of the 14.5



offset between the observed

and predicted positions of the 65 Ma Suiko seamount on the Emperor

continuation of the Hawaiian hotspot track (Figure T15). They also

discuss the integrity of the Pacific plate and the role of missing plate

boundaries and errors in kinematic plate circuits, and find that they

play a small role. Di Venere and Kent (1999) conclude that most of

the apparent motion between the two main groups of hotspots is real,

with an average drift of about 25 km myr

1

since 65 Ma. Torsvik et al.

(2002) summarize paleomagnetic tests, which in their view raise increas-

ing doubts on the fixity of hotspots. Though Indo-Atlantic hotspots appear

to have remained stable, the Pacific hotspots, most notably Hawaii, appear

to have drifted southward with respect to the spin axis in the 65–45 Ma

period. Torsvik et al. (2002) conclude that global analyses fail to support

TPW since the late Cretaceous, and suggest controversial, slow TPW in

the early Cretaceous. Their preferred explanation for this is southward

drift of Atlantic hotspots prior to 95 Ma.

Figure T16 Comparison between the “Indo-Atlantic” (open dots

and dashed line) and “Pacific” (squares and solid line) TPW paths

(after Besse and Courtillot, 2002).

962 TRUE POLAR WANDER

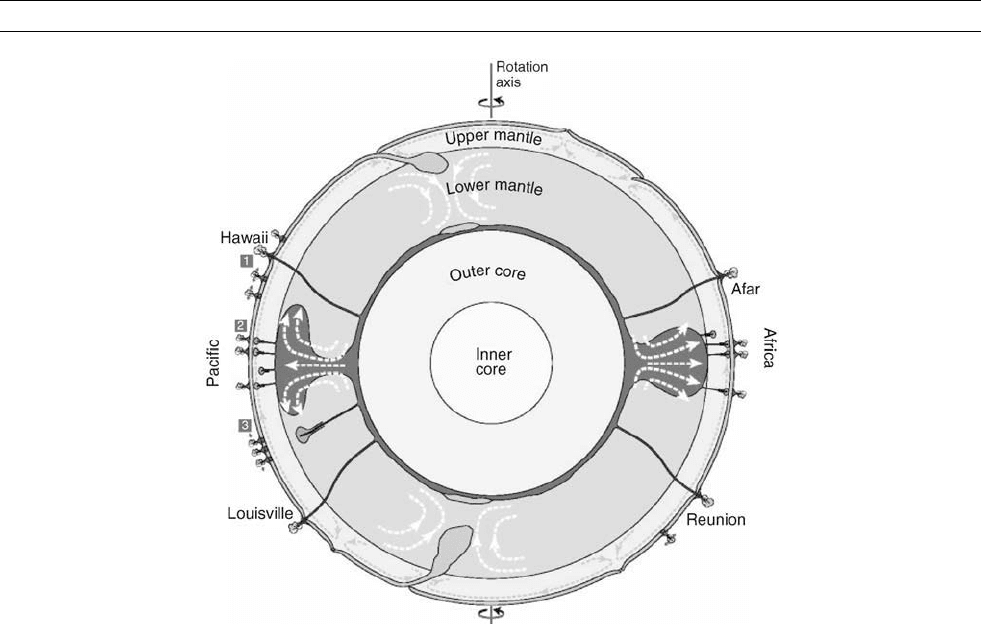
Courtillot et al. (2003) recently reanalyzed the characteristics of the

world catalogue of some 50 hotspots. Based on geophysical (buoy-

ancy, tomography), geochemical (He isotope ratio) and geological

(presence of a seamount track, of a flood basalt) criteria, Courtillot

et al. (2003) suggest that surface hotspots on Earth may have three dis-

tinct origins (Figure T17): at least seven “primary” hotspots (Hawaii,

Easter, Louisville, Iceland, Afar, Reunion, and Tristan da Cunha)

would originate from the deepest part of the lower mantle, possibly

anchored on chemical heterogeneities deposited in the D” layer. Some

20 “secondary” hotspots might originate from the bottom of the tran-

sition zone in relation with the large transient domes that correspond to

the two antipodal superswells under the central Pacific and Africa.

And the remainder (20) could be upper mantle features, as suggested

for instance by Anderson (e.g., 2000). Very recently, Montelli et al.

(2004) have traced the deep roots of some primary plumes into the

lowermost mantle, based on a new type of “finite-frequency” tomo-

graphy. The list of their primary plumes is similar to though not iden-

tical with that of Courtillot et al. (2003).

Restraining themselves to potential primary hotspots, Courtillot

et al. (2003) find no evidence for inter-hotspot motion significantly

larger than 5 km myr

1

either within the Pacific hemisphere or the

Indo-Atlantic hemisphere hotspots (however, in very recent work,

Steinberger et al. (2004) and Koppers et al. (2004) do evidence some

motion between Hawaii and Louisville). Such rms velocities of

5 km myr

1

or less, i.e., an order of magnitude less than rms plate

velocities are to first order “small.” So, some primary hotspots indeed

seem to provide a quasifixed frame in each hemisphere over the last

80–100 myr. Was there then any motion between the two hotspot

ensembles? This raises the well-known difficulty of establishing a reli-

able kinematic connection between the two hemispheres through

Antarctica. This has recently been addressed by Raymond et al.

(2000). Based on updated kinematics, these authors predict the loca-

tion of the Hawaiian hotspot back in time, under the hypothesis that

Reunion and Hawaii have remained fixed with respect to each other;

for this, they use the dated tracks left on the African and Indian plates

by the Reunion hotspot since it started as the Deccan traps 65 Ma ago.

The plot of misfit between the predicted and observed positions for

Hawaii as a function of time (Figure T15) indicates that the two hot-

spots have actually drifted slowly (Figure T18a), at 10 km myr

1

for the last 45 myr, but at a much faster rate (50 km myr

1

) prior

to that (assuming that there is no missing plate boundary or unac-

counted for motion between E and W Antarctica), vindicating earlier

conclusions reached by Tarduno and Cottrell (1997). Courtillot et al.

(2003) conclude that the primary hotspots may form two distinct sub-

sets in each one of the two geodynamically distinct hemispheres. Each

subset would deform an order of magnitude slower than typical plate

velocities. The two subsets would have been in slow motion for the

last 45 myr, but in faster motion prior to that.

Figure T18b,c displays paleomagnetically derived paleolatitudes for

the Hawaii and Reunion hotspots, which can be taken as the best docu-

mented representatives from each hemisphere. However sparse, the

data are compatible with the same simple two-phase history, in which

there was little latitudinal motion in the last 45 myr, but significant

equatorward motion prior to this, at about 50 km myr

1

for Hawaii

and 30 km myr

1

for Reunion. There is an uncertainty of a few myr

(up to 5) on the timing of the change from one phase to the next at

40–50 Ma. The 45 Ma date is most accurately fixed by the age of

the bend of the Hawaiian-Emperor chain, if this is indeed the common

time of change of all processes described in Figure T18, which we

assume to be the case to a first approximation. Tarduno et al. (2003)

report new data from the Emperor seamounts that confirm an age-

progressive paleolatitude trend. The southward drift rate is about

Figure T17 A schematic cross section of the dynamic Earth going through its rotation axis, outlining the possible sources of three types

of plumes/hotspots: “primary,” deeper plumes possibly coming from the lowermost mantle boundary layer; “secondary” plumes

possibly coming from the top of domes near the depth of the transition zone at the locations of the superswells; “tertiary” hotpots may

have a superficial origin (after Courtillot et al., 2003).

TRUE POLAR WANDER 963

40 km myr

1

between 81 and 47 Ma. Tarduno et al. (2003) also conclude

that TPW was smaller than suggested in earlier studies.

The recently re-evaluated estimate of TPW over the last 200 myr

(Figure T12) is uncertain, as recalled above, being based only on hot-

spots from the Indo-Atlantic hemisphere. The TPW curve estimated

using Pacific-only data is similar to the Indo-Atlantic TPW, seemingly

validating to first order the concept that TPW is a global phenomenon

(Figure T16). We have seen that Gordon et al. (2004) believe that

motion between the two subsets of primary hotspots is small enough

that the hotspot reference frame remains useful for estimating TPW

over the past 125 myr On the other hand, Besse and Courtillot

(2002) suggest that TPW pole positions for the two hemispheres are

significantly displaced between 50 and 90 Ma (Figure T16).

Due to the high viscosity of the bulk of the lower mantle (see e.g.,

Lambeck and Johnston, 1998; Steinberger and O’Connell, 2000), the

primary (and probably also the secondary) plumes follow the large-

scale motion of the lower mantle. The two groups of primary hotspots

might indicate that the two separate mega-cells of quadrupolar convec-

tion, centered on the Pacific and African super-upwellings, have

moved little (10 km myr

1

) in the last 40–50 myr with respect

to each other, but underwent some significant (50 km myr

1

), rather

uniform, relative motion in the previous tens of millions of years. This

motion would have already been going on prior to the oldest preserved

trace of the Hawaiian hotspot (e.g., prior to 80 Ma). Hotspot tracks

become fewer and more uncertain as one goes back in the past and

pre-100 Ma TPW estimates should be regarded with caution. However,

there are indications (Besse and Courtillot, 2002) that the phase of

TPW which ended around 50 Ma may have started 130 Ma ago

(Figure T12). What could have triggered it? The geometry of density

anomalies associated with upwellings (notably with the two super-

swells) may not have a large enough effect on the principal axes of

inertia of the Earth and hence on TPW (Richards et al., 1999). How-

ever, because they are antipodal, the direction of maximum principal

axis of inertia is very sensitive to time variations in superswell struc-

ture and some TPW should occur on the same time scale as the super-

swells (with alternating quiet and more rapid episodes) and with an

amplitude which could be similar to that due to subducting slabs

(Greff-Lefftz, 2004). Indeed, cold subducted material may have a lar-

ger effect on TPW (e.g., Ricard et al., 1993a,b). It has been proposed

that this material may accumulate along the great circle of dominant

downwelling in the lower mantle, at the base of subduction zones near

the transition zone, and trigger an avalanche in the lower mantle

Figure T18 Time variations of four significant kinematic, geographic or dynamic indicators of hotspot motion (all on the same time

scale in million years

B.P.). All display a steplike change in velocity at 40–50 Ma. Velocity patterns are shown as full or black lines,

depending on whether the change happened at 40 or 50 Ma. (a) Distance between observed and predicted positions for the Hawaiian

hotspot. (b) and (c) Latitudinal evolution of the Hawaiian and Reunion hotspots. (d) Along track TPW velocity at 10Ma intervals (after

Courtillot et al., 2003; Tarduno et al., 2003).

964 TRUE POLAR WANDER

(Weinstein, 1993; Steinbach et al., 1994; Brunet and Machetel, 1998).

Such an avalanche starting some 130 Ma ago could have set Earth on

the episode of TPW which lasted until 40–50 Ma ago. An alternate

interpretation would be the disappearance of a major subduction

zone system, after which both heat flow and mean temperature would

have been rapidly and significantly altered (S. Labrosse and L.-E.

Ricou, personal communication, 2002). The more recent halting of

TPW at 40–50 Ma could also be related to the closure of the huge

Tethys subduction zone, following the generalization of Indian collision,

as has been suggested for a long time in order to interpret the Hawaii-

Emperor bend (Patriat and Achache, 1984). Episodes of TPW could

be the result of such (rare) events, with alternate episodes of quiescence

lasting tens of millions of years. And primary hotspots would be our

main source of information on their time history, if they can be consid-

ered as tracers of readjustments in the two-cell geometry of the lower-

mantle reservoirs.

Modeling of true polar wander

Modeling of TPW has made significant progress in the last decade.

In an early attempt, Ricard et al. (1993b) derived a model of mantle

density heterogeneities based on plate motions recorded by the ocean

floor, including slabs crossing the upper/lower mantle transition zone

slowing down by a factor between 2 and 5. Based on this, they com-

puted a synthetic geoid, which agreed rather well with observations,

provided viscosity increased by a factor 40 going from the upper to

the lower mantle. Changes in the degree two geoid should reflect the

history of the inertia tensor and therefore TPW as revealed by paleo-

magnetism. Ricard et al. (1993a) predicted TPW velocities on the

order of 300 km myr

1

in the direction 130



W, much larger than

observed rates. Their three-layer model could not account simulta-

neously for the present-day geoid and observed TPW. Slowing TPW,

i.e., stabilizing the Earth, can be accomplished in two ways. Either

by increasing viscosity at depth and slowing motion of the bulge

(Spada et al., 1992): increasing lower mantle viscosity by a factor

100 rather than 40 slows TPW to a more reasonable 40 km myr

1

but worsens the fit to the geoid. Or by slowing down time changes

in the nonhydrostatic tensor: Richards et al. (1997) explain the

observed long-term stability of the rotation axis by the slow rate of

change in large-scale plate tectonic motions in the last 100 myr.

Subducted lithosphere is for them the main component of mantle

density heterogeneity and invoking readjustment of the rotational

bulge is not necessary (see also early work by Chase, e.g., 1979). They

find that the degree 2 geoid coefficient changes little in the last 60 myr,

and that a lower/upper mantle viscosity ratio of 30 leads to TPW velo-

city estimates less than 50 km myr

1

. The computed synthetic TPW

path they obtain for a model with layered viscosity has some features

which qualitatively resemble observations (Figure T19).

In more recent studies, seismic tomography is used to infer 3D maps

of density heterogeneities that drive flow in the viscous mantle. Stein-

berger and O’Connell (2002; see also Steinberger, 1996) have devel-

oped an algorithm to calculate changes in the Earth ’s rotation axis

for rather general viscoelastic Earth models. They combine hotspot

motion, polar wander and plate motions in a single dynamically con-

sistent model (though plate velocities are imposed on the model, not

derived from it), allowing all effects to be simultaneously determined

and their relative effects sorted out. Changes in rotation are due to

advection of “realistic” density anomaly distributions inferred from a

number of seismic tomography models in a “realistic” flow field

constrained by observed plate kinematics at the surface. The axis of

maximum hydrostatic moment of inertia is by definition parallel to

the rotation axis, and one of the principal axes of the “total” nonhydro-

static inertia tensor (see section “Definitions and early views”) always

follows the rotation axis closely, as originally pointed out by Spada

et al. (1996a,b). This alignment does not imply an alignment with

the axis of maximum “total” (Ricard et al., 1993a) or “imposed” non-

hydrostatic moment of inertia; because of delayed adjustment of the

bulge, a misalignment may result (Steinberger and O’Connell, 2002).

But this is negligible unless the viscosity of the lower mantle is

much larger than 10

Pas (and except in the hypothetical case of

inertial interchange, see section “Inertial interchange and true polar

Figure T19 (a) A comparison of TPW observations and models

over the past 100myr. Open circles are for observation derived

determinations by Besse and Courtillot (2002; see Figures T12

and T16); gray circles are a model calculation with 2-layer mantle

viscosity structure—viscosity ratio of 30—by Richards et al.

(1997); the solid line with tick marks is from a model calculation

by Steinberger and O’Connell (2002), with an 8-layer mantle

viscosity structure and driving density heterogeneities calculated

from a tomographic model of Grand (2001 personal

communication to the authors of that paper). Note that this is a

corrected curve (see text). (b) A comparison of the TPW curve of

Besse and Courtillot (2002) for the past 80Ma and a “mean

mantle” apparent polar wander path derived by B. Steinberger

(personal communication, 2004) from the BC02 synthetic

apparent polar wander path for South Africa (Table 4, with

correction given in Besse and Courtillot, 2003) and finite African

plate rotation in the mean mantle reference frame for the

“preferred” model of Steinberger et al. (2004).

TRUE POLAR WANDER 965