Gubbins D., Herrero-Bervera E. Encyclopedia of Geomagnetism and Paleomagnetism

Подождите немного. Документ загружается.

the well known Mie-Grüneisen equation of state. At low temperatures,

where only harmonic phonons contribute to E

and P

, g should indeed

be temperature independent above the Debye temperature, because

¼ 3k

T per atom, and P

V ¼ –3k

T(dlno/dlnV ) ¼ 3k

so that g ¼ g

(the phonon Grüneisen parameter), which depends only

on V. But at high temperatures, the temperature independence of g will

clearly fail because of electronic excitations and anharmonicity. Calcu-

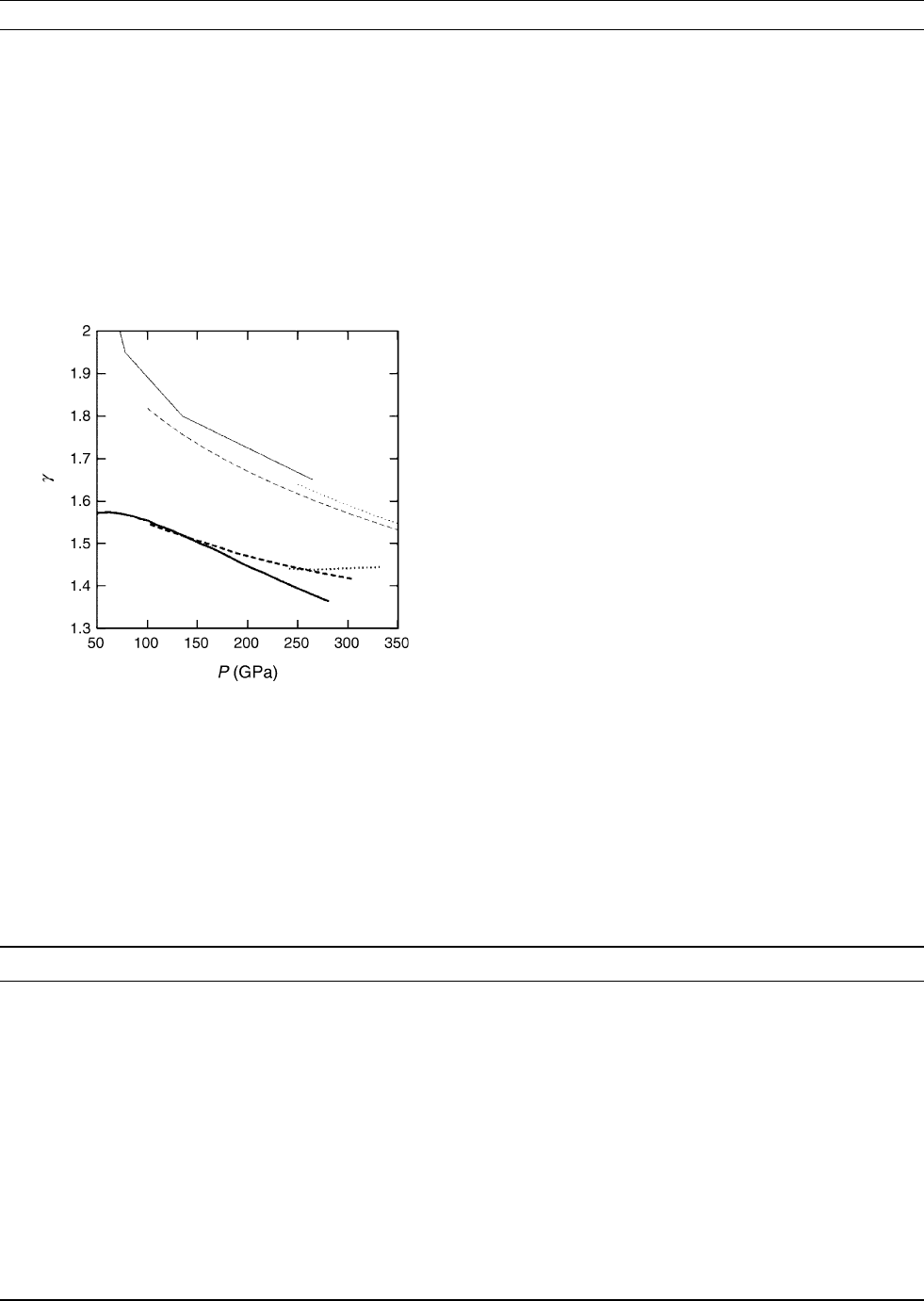
lated results for g (Figure C31) indicate that it varies rather little with

either pressure or temperature in the region of interest. At temperatures

below 4000 K, it decreases with increasing pressure, as expected from

the behavior of g

. This is also expected from the often-used empirical

rule of thumb g ¼ (V/V

)

, where V

is a reference volume and q is a

constant exponent usually taken to be roughly unity. Since V decreases

by a factor of about 0.82 as P goes from 100 to 300 GPa, this empirical

relation would make g decrease by the same factor over this range, which

is roughly what we see. However, the pressure dependence of g is very

much weakened as T increases until, at 6000 K, g is almost constant.

The measured and calculated elastic constants of hcp-Fe are pre-

sented in Table C4. Although there is some scatter on the reported

values of c

, overall, the agreement between the experimental and

various ab initio studies are excellent.

Rheological and thermodynamical properties

of liquid Fe

De Wijs et al. (1998) in Alfè et al. (2000) have reported the quantum

mechanically determined viscosity, diffusion, and thermodynamic

properties of Fe in the liquid state. Their simulations cover the tem-

perature range 3000–8000 K and the pressure range 60–390 GPa.

Table C5 shows a comparison of the pressures calculated in the simu-

lations with the pressures deduced by Anderson and Ahrens (1994)

from a conflation of experimental data, and Figure C32a-e summarizes

for liquid Fe the calculated values of density, thermal expansion coef-

ficient, adiabatic and isothermal bulk moduli, heat capacity (C

), and

Grüneisen parameter. These values are in close accord with the esti-

mates available in Anderson and Ahrens (1994). It is worth noting that

the systematics of the behavior of heat capacity (C

), Grüneisen para-

meter, etc., for liquids is quite different for those of solids.

Table C6 reports the calculated values for the self diffusion of Fe

in liquid Fe, and the viscosity of liquid Fe for the same range of

P and T conditions reported above. For the entire pressure-tempera-

ture domain of interest for the Earth’s outer core, the diffusion coeffi-

cient, D, and viscosity, , are comparable with those of typical simple

liquids, D being 5  10

–9

–1

and  being in the range 8–15 mPa

s, depending on the detailed thermodynamic state.

Conclusion

The past decade has seen a major advance in the application of

ab initio methods in the solution of high pressure and temperature

geophysical problems, thanks to the rapid developments in high-

performance computing. The progress made means that it is now

Table C4 A compilation of elastic constants (c

, in GPa), bulk (K) and shear (G) moduli (in GPa), and longitudinal (v

) and

transverse (v

) sound velocity (in km s

1

) as a function of density (r,ingcm

3

) and atomic volume (in A

per atom). In this table

K ¼ (<c

> þ 2<c

>)/3 and G ¼ (<c

> – <c

> þ 3<c

>)/5, where <c

> ¼ (c

þ c

)/3, etc. Previous calculated

values are from Stixrude and Cohen (1995), Steinle-Neumann et al. (1999), So

derlind et al. (1996), and Voc

adlo et al. (2003b).

The experimental data of Mao et al. (1999) is also presented

V r c

KG v

Stixrude and Cohen 9.19 10.09 747 301 297 802 215 223 454 224 8.64 4.71

7.25 12.79 1697 809 757 1799 421 444 1093 449 11.50 5.92

Steinle-Neumann et al. 8.88 10.45 930 320 295 1010 260 305 521 296 9.36 5.32

7.40 12.54 1675 735 645 1835 415 470 1026 471 11.49 6.13

6.66 13.93 2320 1140 975 2545 500 590 1485 591 12.77 6.51

Mao et al. 9.59 9.67 500 275 284 491 235 113 353 160 7.65 4.06

7.36 12.60 1533 846 835 1544 583 344 1071 442 11.48 5.92

Söderlind et al. 9.70 9.56 638 190 218 606 178 224 348 200 8.02 4.57

7.55 12.29 1510 460 673 1450 414 525 898 448 11.03 6.04

6.17 15.03 2750 893 1470 2780 767 929 1772 789 13.70 7.24

Vocadlo et al. 9.17 10.12 672 189 264 796 210 242 397 227 8.32 4.74

8.67 10.70 815 252 341 926 247 282 492 263 8.87 4.96

8.07 11.49 1082 382 473 1253 309 350 675 333 9.86 5.38

7.50 12.37 1406 558 647 1588 381 424 900 407 10.80 5.74

6.97 13.31 1810 767 857 2007 466 522 1177 500 11.77 6.13

6.40 14.49 2402 1078 1185 2628 580 662 1592 630 12.95 6.59

Figure C31 The Gru

neisen parameter (g) of hcp-Fe as a function

of pressure on isotherms T ¼ 2000 K (continuous curves), 4000 K

(dashed curves), and 6000 K (dotted curves). Heavy and light

curves results of Alfe

et al. (2000) and of Stixrude et al. (1997),

respectively.

96 CORE PROPERTIES, THEORETICAL DETERMINATION

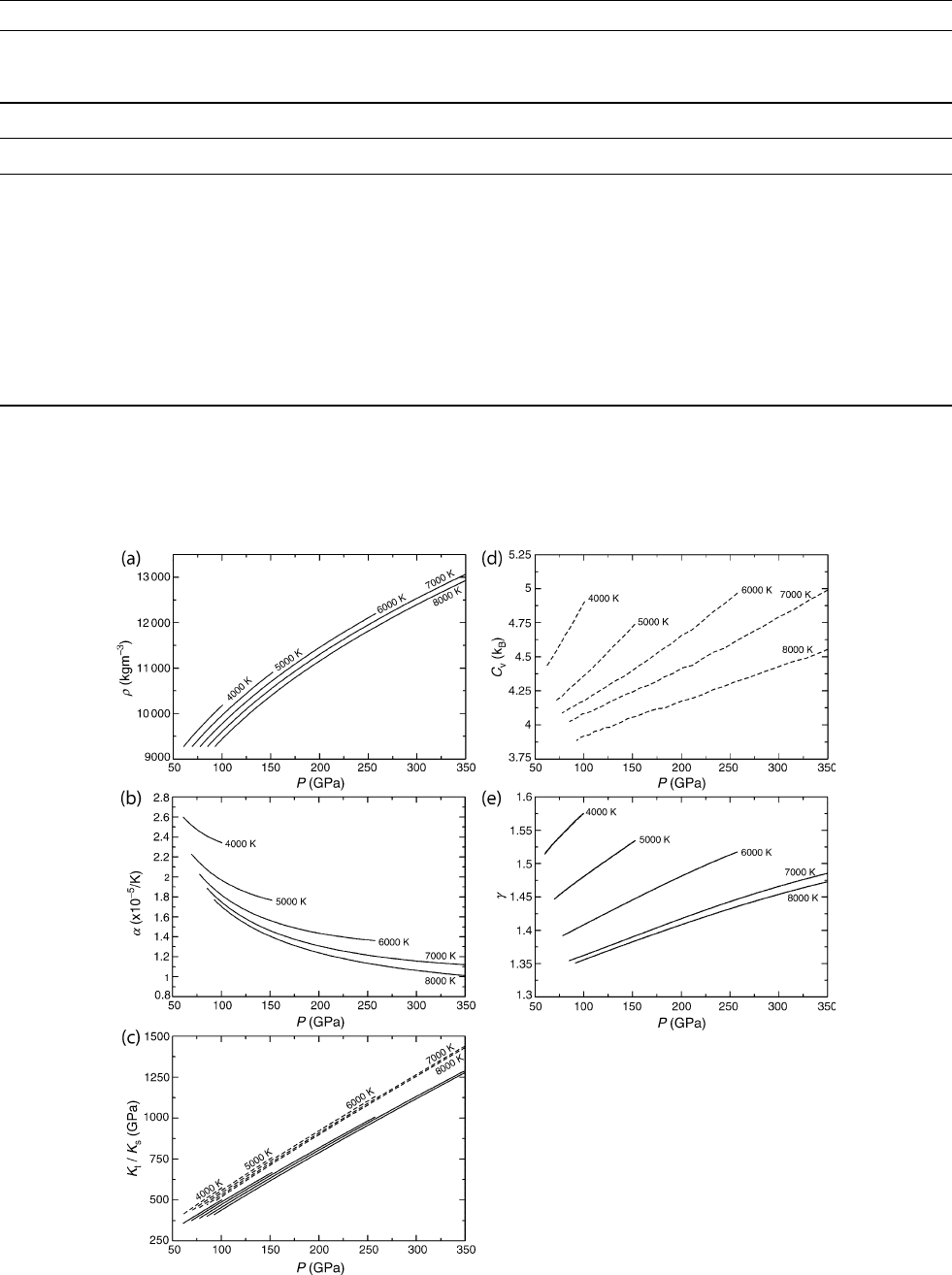
Table C5 Pressure (in GPa) calculated as a function of temperature (T) and density for liquid Fe. Experimental estimates are in

parentheses, from Anderson and Ahrens (1994)

r (kg m

3

)

T (K) 9540 10700 11010 12130 13300

3000 60

4300 132

(135)

5000 140

(145)

6000 90 151 170 251 360

(155) (170) (240) (335)

7000 161 181 264 375

(250) (350)

8000 172 191 275 390

(360)

Figure C32 Panel Showing the calculated values for liquid Fe of (a) density, (b) thermal expansion coefficient, (c) adiabatic (dashed

lines) and isothermal bulk (soild lines) moduli, (d) heat capacity (C

), and (e) Gru

neisen parameter, all as a function of P at temperatures

between 4000 and 8000 K.

CORE PROPERTIES, THEORETICAL DETERMINATION 97

possible to calculate from first principles the free energies of solid and

liquid phases, and hence to determine both the phase relations and the

physical properties of planetary-forming minerals. In the future, with

“tera-scale computing,” it will be possible to model more complex and

larger systems to investigate for example solid-state rheological pro-

blems or physical properties such as thermal and electrical conductivity,

which are currently beyond current quantum mechanical simulations.

David Price

Bibliography

Alfè, D., Kresse, G., and Gillan, M.J., 2000. Structure and dynamics of

liquid Iron under Earth’s core conditions. Physical Review, 61:

132–142.

Alfè, D., Price, G.D., and Gillan, M.J., 2001. Thermodynamics of

hexagonal-close-packed iron under Earth’s core conditions. Physi-

cal Review, B64: 045123.

Alfè, D., Price, G.D., and Gillan, M.J., 2002. Iron under Earth’s core con-

ditions: Liquid-state thermodynamics and high-pressure melting curve

from ab initio calculations. Physical Review, B65: 165118, 1–11.

Anderson, W.W., and Ahrens, T.J., 1994. An equation of state for

liquid iron and implication for the Earth’s core. Journal of Geophy-

sical Research, 99: 4273–4284.

Brown, J.M., and McQueen, R.G., 1986. Phase transitions, Grüneisen

parameter and elasticity for shocked iron between 77 GPa and

400 GPa. Journal of Geophysical Research, 91: 7485–7494.

Duffy, T.S., and Ahrens, T.J., 1993. Thermal-expansion of mantle

and core materials at very high-pressures. Geophysical Research

Letters, 20: 1103–1106.

Mao, H.K., Shu, J., Shen, G., Hemley, R.J., Li, B., and Sing, A.K.,

1999. Elasticity and rheology of iron above 220GPa and the nature

of the Earth’s inner core. Nature, 399: 280.

Matsui, M., and Anderson, O.L., 1997. The case for a body-centred

cubic phase for iron at inner core conditions. Physics of Earth

and Planetary Interiors, 103:55–62.

Söderlind, P., Moriarty, J.A., and Wills, J.M., 1996. First-principles

theory of iron up to earth-core pressures: Structural, vibrational

and elastic properties. Physical Review, B53: 14063–14072.

Steinle-Neumann, G., Stixrude, L., and Cohen, R.E., 1999. First-

principles elastic constants for the hcp transition metals Fe, Co,

and Re at high pressure. Physical Review, B60: 791–799.

Stixrude, L., and Cohen, R.E., 1995. Constraints on the crystalline

structure of the inner core—mechanical instability of bcc iron at

high-pressure. Geophysical Research Letters, 22: 125–128.

Stixrude, L., Wasserman, E., and Cohen, R.E., 1997. Composition and

temperature of the Earth’s inner core. Journal of Geophysical

Research, 102: 24729–24739.

Vo čadlo, L., deWijs, G.A., Kresse, G., Gillan, M.J., and Price, G.D.,

1997. First principles calculations on crystalline and liquid iron at

Earth’s core conditions. Faraday Discussions, 106: 205–217.

Vo čadlo, L., Brodholt, J., Alfè, D., Price, G.D., and Gillan, M.J., 1999.

The structure of iron under the conditions of the Earth’s inner core.

Geophysical Research Letters, 26: 1231–1234.

Vo čadlo, L., Alfè, D., Gillan, M.J., Wood, I.G., Brodholt, J.P.,

and Price, G.D., 2003a. Possible thermal and chemical stabilisa-

tion of body-centred-cubic iron in the Earth’s core? Nature, 424:

536–553.

Vo čadlo, L., Alfè, D., Gillan, M.J., and Price, G.D., 2003b. The

Properties of iron under core conditions from first principles

calculations. Physics of Earth and Planetary Interiors, 140:

101–125.

Cross-references

Core Density

Core Properties, Physical

Core Temperature

Core Viscosity

Core, Adiabatic Gradient

Grüneisen’s Parameter for Iron and Earth’s Core

Inner Core Anisotropy

Inner Core Seismic Velocities

Melting Temperature of Iron in the Core, Experimental

Melting Temperature of Iron in the Core, Theoretical

Shock Wave Experiments

CORE TEMPERATURE

High-pressure experiments combined with geophysical and geodynamic

modeling suggest that the temperature near the bottom of the mantle

probably lies between 2500 and 3000 K. There is still uncertainty over

the heat flow out of the core and the thermal conductivity of the mate-

rials in D

zone, so it is not possible to give a precise estimate of the

temperature increas e across the thermal boundary layer at the base of

the mantle, although it is generally accepted that this may be of the

order of 1000 K. Another approach to constraining the temperature

of the core is based upon the assumption that the solid inner core is

crystallizing from the liquid outer core, and the ICB marks a crystalli-

zation interface. Given that the core is iron (alloyed with about 10% of

lighter elements), and given that impurities lower the melting point,

then the melting temperature (T

) of iron at the pressure of the ICB

can be used to place an upper bound on the core’s temperature at this

Table C6 The diffusion coefficient (D) and the viscosity () from our ab initio simulations of liquid Fe at a range of temperatures

and densities. The error estimates come from statistical uncertainty due to the short duration of the simulations

r (kg m

3

)

T (K) 9540 10700 11010 12130 13300

D (10

9

1

) 3000 4.0  0.4

4300 5.2  0.2

5000 7.0  0.7

6000 14  1.4 10  19 0.9 6  0.6 5  0.5

7000 13  1.3 11  1.1 9  0.9 6  0.6

 (mPas) 3000 6  3

4300 8.5  1

5000 6  3

6000 2.5  25 27 38 315 5

7000 4.5  24 28 310 3

98 CORE TEMPERATURE

depth. As reviewed elsewhere in this volume (see Melting temperature

of iron in the core, experimental and Melting temperature of iron in the

core, theory) estimates for T

can be obtained from shock melting

experiments, by laser-heated diamond-anvil cells studies, and from

theory. The experimental measurements are difficult and their interpre-

tation is controversial, with ICB melting temperatures inferred from

experiments ranging from 4850 K (Boehler, 1996) to 6850 K

(Yoo et al., 1993). Values from theory, however, now seem to be more

closely clustered, with values of T

of Fe at 360 GPa of between 6000

and 6400 K (see Melting temperature of iron in the core, theory).

However, to constrain the temperature at the ICB more tightly, it is

essential to infer an estimate of the true composition of the core and

to determine the resulting suppression of the melting temperature

caused by the light alloying elements.

On the basis of seismology and data for pure Fe, it is considered that

the outer and inner core contain some light element impurities (see

Core composition). Cosmochemical abundances of the elements, com-

bined with models of the Earth’s history, limit the possible impurities

to a few candidates. Those most often discussed are S, O, and Si (e.g.,

Poirier, 1994; Allègre et al., 1995), and most studies are, to date, con-

fined to these three alloying elements. Boehler (2000) reviews the high

P melting studies done on Fe-O and Fe-S systems, and concludes that

the in situ detection of the solidus in such experiments is difficult

because of the small melt fraction produced at the eutectic temperature

in a multicomponent system. Nevertheless, he claims that experiments

suggest that alloying elements in Fe produce only a small depression

in T

. This contrasts with historical estimates (Stevenson, 1981) of the

effect of, for example, S on the T

of Fe at core pressures, which indi-

cated that a suppression of 1100 K should be expected.

To address this problem, Alfè et al. (2002 a,b) have recently devel-

oped a strategy that uses quantum mechanical molecular dynamics to

both constrain seismologically and thermodynamically allowed com-

positions for the outer and inner core, and to determine the magnitude

of alloy-induced suppression of the melting temperature of Fe at the

ICB. Their approach is based on the supposition that the solid inner

core is slowly crystallizing from the liquid outer core and that there-

fore the inner and outer cores are in thermodynamic equilibrium at

the ICB. This implies that the chemical potentials of Fe and of each

impurity must be equal on the two sides of the ICB. If the core con-

sisted of pure Fe, equality of the chemical potential (Gibbs free energy

in this case) would tell us only that the temperature at the ICB is equal

to the melting temperature of Fe at the ICB pressure of 330 GPa. With

impurities present, equality of the chemical potentials for each impur-

ity element imposes a relation between the mole fractions in the liquid

and the solid, so that with S, O, and Si there are three such relations.

But these three relations must be consistent with the inferred values

of the mass densities in the inner and outer core deduced from seismic

and free-oscillation data.

The chemical potential, m

, of a solute X in a solid or liquid solution

is conventionally expressed as m

¼ m

þ k

T ln a

, where m

is a

constant and a

is the activity. It is common practice to write a

¼ g

where g

is the activity coefficient and c

the concentration of X.

The chemical potential can therefore be expressed as

¼ m

þ k

T ln g

(Eq. 1)

which can be rewritten as

¼ m



þ k

T ln c

(Eq. 2)

It is helpful to focus on the quantity m

* for two reasons: first, because

it is a convenient quantity to obtain by ab initio calculations (Alfè

et al., 2002b); second, because at low concentrations the activity coef-

ficient, g

, will deviate only weakly from unity by an amount propor-

tional to c

and by the properties of the logarithm the same will be true

of m

The equality of the chemical potentials m

and m

in coexisting

liquid and solid (superscripts l and s, respectively) then requires that

l

þ k

T ln c

¼ m

s

þ k

T ln c

(Eq. 3)

or equivalently

¼ exp ½ðm

l

 m

s

Þ=k

T (Eq. 4)

This means that the ratio of the mole fractions c

and c

in the solid

and liquid solution is determined by the liquid and solid thermody-

namic quantities m

l

and m

s

. Although liquid-solid equilibrium in

the Fe/S and Fe/O systems has been experimentally studied up to pres-

sures of around 60 GPa, there seems little prospect of obtaining experi-

mental data for m

l

 m

s

for Fe alloys at the much higher ICB

pressure. However, Alfè et al. (2002 b) have recently shown that the

fully ab initio calculation of m

l

and m

s

is technically feasible. Thus,

the chemical potential, m

, of chemical component X can be defined

as the change of Helmholtz free energy when one atom of X is intro-

duced into the system at constant temperature T and volume V.

In ab initio simulations, it is awkward to introduce a new atom, but

the awkwardness can be avoided by calculating m



 m



, which is

the free energy change, DF, when an Fe atom is replaced by an X

atom. For the liquid, this DF is computed by applying the technique

of “thermodynamic integration” to the (hypothetical) process in which

an Fe atom is continuously transmuted into an X atom.

Alfè et al. find a major qualitative difference between O and the

other two impurities. For S and Si, m



is almost the same in the solid

and the liquid, the differences being at most 0.3 eV, i.e., markedly

smaller than k

T 0.5 eV; but for O the difference of m



between solid

and liquid is 2.6 eV, which is much bigger than k

T. This means that

added O will partition strongly into the liquid, but added S or Si will

have similar concentrations in both the solid and the coexisting liquid

phase.

Their simulations of the chemical potentials of the alloys can be

combined with simulations of their densities to investigate whether

the known densities of the liquid and solid core can be matched by

any binary Fe/X system, with X ¼ S, O, or Si. Using their calculated

partial volumes of S, Si, and O in the binary liquid alloys, one finds

that the mole fractions required to reproduce the liquid core density

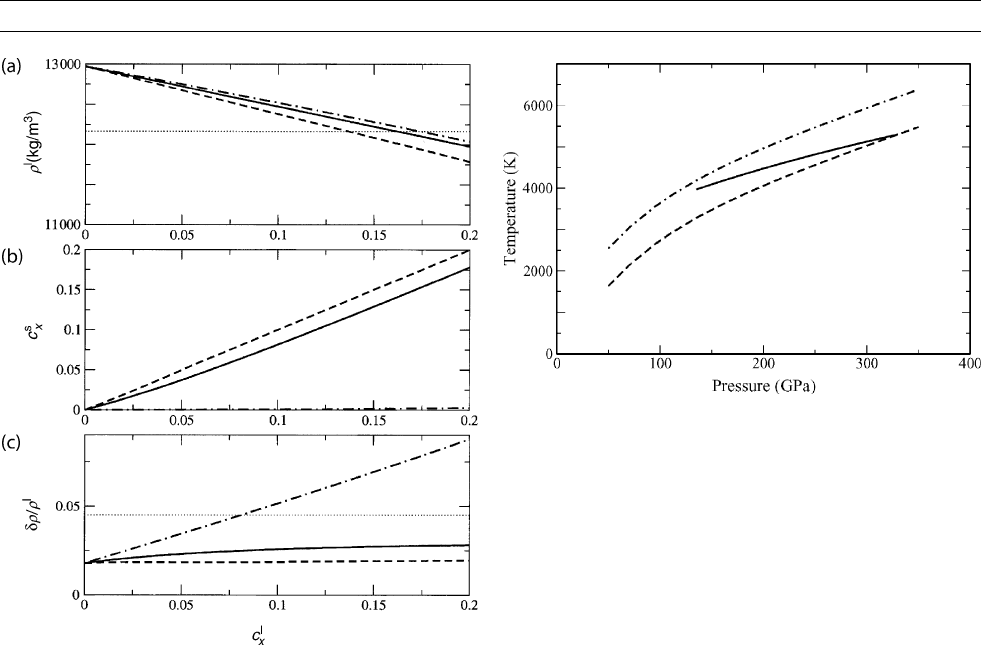
are 16%, 14%, and 18% respectively (Figure C33, panel (a) displays

the predicted liquid density as a function of c

compared with the seis-

mic density). The calculated chemical potentials in the binary liquid

and solid alloys then give the mole fractions in the solid of 14%,

14%, and 0.2%, respectively, that would be in equilibrium with these

liquids (see Figure C33, panel (b)). Finally, the partial volumes

in the binary solids give ICB density discontinuities of 2.7 0.5,

1.8 0.5 and 7.8 0.2%, respectively (Figure C33, panel (c)).

As expected, for S and Si, the discontinuities are considerably smaller

than the known value of 4.5 0.5%; for O, the discontinuity is

markedly greater than the known value. Alfè et al. conclude that none

of the binary systems can account for the discontinuity quantitatively.

The density and seismic character of the core can, however, be accounted

for by O together with either or both of S and Si. Ab initio calculations on

general quaternary alloys containing Fe, S, O, and Si will clearly be fea-

sible in the future, but currently they are computationally too demand-

ing, so for the moment it is assumed that the chemical potential of each

impurity species is unaffected by the presence of the others. This led Alfè

et al. to estimate that the mole fractions needed to account for the ICB

density discontinuity were 8.5  2.5 mole % S (and/or Si) and 0.2 

0.1% O in the inner core and 10  2.5% S/Si and 8  2.5% O in the

liquid outer core. This compositional estimate is based on the value of

the density discontinuity at the ICB determined by Shearer and Masters

(1990). Since then, Masters and Gubbins (2003) have reassessed the free

oscillation data set and have determined the density jump at the ICB to be

CORE TEMPERATURE 99

0.82  0.18 Mg m

3

, which is larger than the previous estimates. Using

the new density data of Masters and Gubbins leads to a revised core com-

position of 7  2.5 mole % S/Si and 0.2  0.1% O for the inner core and

8  2.5% S/Si and 13  2.5% O for the outer core. This sensitivity

emphasizes the need for very accurate seismic data if the composition

of the core is to be constrained more precisely (see also recen t studies

by Koper and Pyle (2004) and Cao and Romanowicz (2004)). Finally,

we should note that Braginsky and Roberts (1995) have considered the

effect of S, Si, and O on core convection and the geodynamo. They con-

cluded on the basis of their dynamical studies, however, that silicon or

sulfur would be favored over oxygen as the principal light alloying con-

stituent. The conflict between their conclusions and the atomistic-based

deductions of Alfè et al. is still to be resolved.

Using however the calculated impurity chemi cal potentials of Alfè

et al., it is possible to use the Gibbs-Duhem relation to compute the

change in the Fe chemical potential caused by the impurities in the

solid and liquid phases. Alfè et al. (2002b) show that the shift of melt-

ing temperature (D T

) due to the presence of the impurities is

D T

¼ k

ðc

 c

Þ= DS

(Eq. 5)

where k

is Boltzmann ’s constant, D S

is the entropy of melting of the

pure Fe, and c

and c

are the concentration of solute atoms in the solid

inner core and liquid outer core, respectively. From their calculated

values it is clear that the suppression of the core melting temperature

( DT

) is dominated by the effect of O, and is approximately –900 K

depending upon the exact value of the density contrast at the ICB.

Using their ab initio estimate of the melting temperature of pure

Fe (see Melting temperature of iron in the core, theory ) at core pres-

sure, Alfè et al. predict that the Earth ’s temperature at the ICB to be

 5300  300 K.

There now appears to be an emerging consensus on the temperature

of the ICB, as the value inferred from the work of Alfè et al.

( 5300  300 K) is close to the value of 5700 K inferred by

Steinle-Neum ann et al. (2001) from independently determined

ab initio calculations on the elastic properties of the inner core and

to the values favored by Poirier and Shankland (1993 ) and that of

5050  300 K suggested by Anderson (2003). It appears now that

only the results inferred from diamond anvil cell (DAC) studies (Boeh-

ler, 1996, 2000) lie outside this region of agreement, with these experi-

ments suggesting that the temperature at the ICB is less than 4800 K. The

origin for the disagreement between melting temperatures inferred from

DAC studies and those obtained from shock data and theory is still to be

satisfactorily explained.

This notwithstanding, given the temperature of the ICB, it is possi-

ble to calculate the temperature of the core at the CMB, assuming that

the outer core temperature profile is adiabatic since

] T =] r ¼ ggT = F (Eq. 6)

where F is the seismic parameter, g is the Grüneisen parameter in

the liquid outer core, and g is the acceleration due to gravity (see also

Figure C34). As with T

ICB

, there is an emerging consensus about the

value of g for the liquid core, with ab initio values (e.g., Vo č adlo

et al., 2003) and those inferred from thermodynamic relations (e.g.,

Anderson, 2003) both finding g to be virtually constant along the adia-

bat, with a value of 1.5 (however, see Stacey and Davis (2004), who

favor a lower value of g). Using the ab initio value and the melting

behavior of Fe alloy determined by Alfè et al. leads to an entirely

ab initio estimate of the core temperature at the CMB of between

4000  300 K. Again, this is in excellent agree ment with that inferred

from thermodynamic arguments (Anderson, 2003), and coincidentally

identical to the value inferred by Boehler (1996), although in this case

the agreement is fortuitous, as Boehler ’ s assumed outer core adiabat is

much shallower than that used in other studies.

Figure C33 Liquid and solid impurity mole fractions c

and c

of impurities X ¼ S, Si, and O and resulting densities of the inner

and outer core predicted by ab initio simulations. Solid, dashed

and chain curves represent S, Si, and O, respectively. (a) Liquid

density r

(kg m

–3

); horizontal dotted line shows density from

seismic data. (b) Mole fractions in solid resulting from equality

of chemical potentials in solid and liquid. (c) Relative density

discontinuity (dr/r

) at the ICB; horizontal dotted line is the value

from free oscillation data.

Figure C34 The calculated melting curve of Fe (chained line),

the suppressed melting curve of Fe-alloy in the core assuming

that DT

is independent of depth (dash line), and the resulting

adiabatic temperature profile (solid line) for the outer core

obtained using Eq. (6).

100 CORE TEMPERATURE

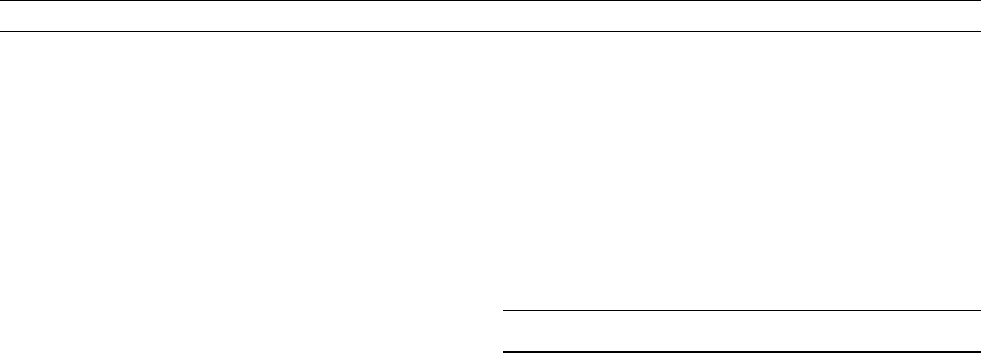
In conclusion, there seems to be growing agreement over the tem-

perature of the core at the ICB and at the CMB. However, more work

is still needed to define the density contrast at the ICB, as it critically

effects models for the composition of the core (which in turn deter-

mine the value of DT

). Also it is essential that the experimentally

and theoretically derived values of the T

of Fe at ICB conditions be

reconciled. Until these issues are resolved, the exact temperature pro-

file in the core will remain contentious.

David Price

Bibliography

Alfè, D., Gillan, M.J., and Price, G.D., 2002a. Composition and tem-

perature of the Earth’s core constrained by combining ab initio cal-

culations and seismic data. Earth and Planetary Science Letters,

195:91–98.

Alfè, D., Gillan, M.J., and Price, G.D., 2002b. Ab initio chemical

potential of solid and liquid solutions and chemistry of the Earth’s

core. Journal of Chemical Physics, 116: 7127–7136.

Allègre, C.J., Poirier, J.P., Humler, E., and Hofmann, A.W., 1995. The

chemical composition of the Earth. Physics of Earth and Planetary

Interiors, 134: 515–526.

Anderson, O.L., 2003. The three-dimensional phase diagram of iron.

In Dehant, V., Creager, K.C., Karato, S-I., and Zatman, S. (eds.),

Earth Core. Geodynamics Series, 31. Washington, D.C.: American

Geophysical Union, pp. 83–104.

Boehler, R., 1996. Melting temperature of the Earth’s Mantle and

Core. Annual Review of Earth and Planetary Sciences, 24:15–40.

Boehler, R., 2000. High-pressure experiments and the phase diagram

of lower mantle and core materials. Reviews of Geophysics, 38:

221–245.

Braginsky, S.I., and Roberts, P.H., 1995. Equations governing convec-

tion in earths core and the geodynamo. Geophysical and Astrophy-

sical Fluid Dynamics, 79:1–97.

Cao, A.M., and Romanowicz, B., 2004. Constraints on density and

shear velocity contrasts at the inner core boundary. Geophysical

Journal International., 157(3): 1146–1151.

Koper, K.D., and Pyle, M.L., 2004. Observations of PkiKP/PcP

amplitude ratios and implications for Earth structure at the bound-

aries of the liquid core. Journal of Geophysical Research-Solid

Earth, 109(B3): art. no. B03301.

Masters, G., and Gubbins, D., 2003. On the resolution of density within

the Earth. Physics of Earth and Planetary Interiors, 140: 159–167.

Poirier, J.P., 1994. Light elements in the Earth’s outer core: A critical

review.

Phys. Earth Planet. Inter., 85: 319–337.

Poirier, J.P., and Shankland, T.J., 1993. Dislocation melting of iron and

the temperature of the inner-core boundary, revisited. Geophysical

Journal International, 115: 147–151.

Shearer, P.M., and Masters, G., 1990. The density and shear velocity

contrast at the inner core boundary. Geophysical Journal Interna-

tional, 102: 491–498.

Stacey, F.D., and Davis, P.M., 2004. High pressure equations of state

with applications to the lower mantle and core. Physics of the

Earth and Planetary Interiors, 142: 137–184.

Steinle-Neumann, G., Stixrude, L., Cohen, R.E., and Gülseren, O.,

2001. Elasticity of iron at the temperature of the Earth’s inner core.

Nature, 413:57– 60.

Stevenson, D.J., 1981. Models of the Earth’score.Science, 214:611–619.

Vo čadlo, L., Alfè, D., Gillan, M.J., and Price, G.D., 2003. The Properties

of Iron under Core Conditions from First Principles Calculations.

Physics of Earth and Planetary Interiors, 140:101–125.

Yoo, C.S., Holmes, N.C., Ross, M., Webb, D.J., and Pike, C., 1993.

Shock temperatures and melting of iron at Earth core conditions.

Physical Review Letters, 70: 3931–3934.

Cross-references

Core Density

Core Properties, Physical

Core Properties, Theoretical Determination

Core, Adiabatic Gradient

Grüneisen’s Parameter for Iron and Earth’s Core

Inner Core Seismic Velocities

Melting Temperature of Iron in the Core, Experimental

Melting Temperature of Iron in the Core, Theory

Shock Wave Experiments

CORE TURBULENCE

Introduction

Turbulence is a ubiquitous feature of geophysical flows. The challenge

in dealing with turbulence is the broad range of spatial and temporal

scales. For the Earth’s core, the largest scales of motion ðL  10

mÞ

are set by the geometry of the core, whereas the smallest dissipative

scales ðl < 0:1mÞ are determined by the low viscosity and chemical dif-

fusivity of liquid iron alloys (Dobson, 2000; Vocadlo et al., 2000). The

range of time scales is even greater (Hollerbach, 2003). Buoyancy-dri-

ven inertial oscillations have diurnal periods (Zhang, 1994), whereas

changes in the frequency of magnetic reversals occur on time scales

of 10

years (McFadden and Merrill, 2000). Such a vast range of spatial

and temporal scales prohibits direct simulations of the Earth’s geo-

dynamo (q.v.). Instead, modelers must confine their attention to the

largest scales and deal with the problem of limited spatial resolution

by parameterizing processes that operate at subgrid scales. Spatially

constant eddy diffusivities or hyperdiffusivities are routinely used

to represent the effects of small-scale flow in geodynamo models

(Glatzmaier and Roberts, 1995, 1996; Kageyama and Sato, 1997; Kuang

and Bloxham, 1997; Kida et al., 1997; Christensen et al., 1998, 1999;

Grote et al., 1999; Kono and Sakuraba, 2000). Even though many

of these models are capable of reproducing features of the Earth’s

field (dipole dominance, episodic reversals, etc.), there is little doubt that

simple models based on scalar diffusivities are inadequate representa-

tions of the small-scale processes (Buffett, 2003). Theoretical studies

(Braginsky and Meytlis, 1990; Shimizu and Loper, 1997) and numerical

simulations (St. Pierre, 1996; Matsushima et al., 1999) have shown

that small-scale motion is likely to be highly anisotropic due to the influ-

ence of rotation and a strong, large-scale magnetic field. Turbulence

in the core is expected to have a plate-like structure, which affects the

transport of heat and momentum at small scales. The influence of this

anisotropy on the large-scale flow is presently unknown.

The nature of turbulence in the core differs in several important

respects from the types of turbulence that are encountered in other

areas of fluid mechanics (e.g., Tennekes and Lumley, 1972). The first

distinction involves the role of the Reynolds number (Re) in character-

izing the flow. The Reynolds number describes the relative importance

of inertia and viscous forces in the momentum equation, so high Re

usually means that inertia has a leading-order role in the dynamics.

This expectation may not be valid when other forces are present.

The value of Re in the Earth’s core is thought to be quite large (per-

haps as large as 10

) by virtue of the low viscosity of liquid iron

and the large size of the core. However, the inertial forces are not

expected to have a leading-order role in the momentum equation,

where the primary force balance includes the Coriolis, Lorentz, and

pressure forces. Large Re in the core means that the effect of inertia

in the core is large compared with the effects of viscosity, but inertia

is still small compared with other forces. This distinction makes the

dynamics of turbulence in the core fundamentally different from that

in other high-Re flows.

CORE TURBULENCE 101

One consequence of this difference is manifest in the spatial distribu-

tion of dissipation in the core. Flow in the core is driven by thermal

and compositional anomalies. These density anomalies are probably dis-

tributed over a very broad range of spatial scales. We expect the work

done by buoyancy forces (e.g., the input of energy to the flow) to be

distributed over an equally broad range of scales. Another expectation,

based on current geodynamo models, is that much of the input energy

is dissipated at the scale where it is supplied (Olson and Christensen,

1999; Buffett and Bloxham, 2001). This view of convection in the core

is strikingly different from high-Re turbulence, where energy is input at

large scales and cascades through a range of progressively smaller scales

until viscous dissipation becomes appreciable. Transfers of energy

between scales still occur in the geodynamo problem. In fact, these

interactions are essential for the operation of the geodynamo (Buffett

and Bloxham, 2001). The subtlety of energy transfers to and from

the small scales make core turbulence an important part of the geo-

dynamo problem.

Eddy diffusion

Eddy diffusion is based on an analogy with molecular transport of heat

and momentum in an ideal gas. The continuum approximation for

molecular transport works well when the average distance between

collisions of molecules, l, is small compared with the scale of the

flow. With the usual assumption that the velocity scale of molecular

motion is proportional to the speed of sound a, the kinetic theory of

gases predicts that the kinematic viscosity of the gas is (Landau and

Lifshitz, 1981)

v  al: (Eq. 1)

The analogy between molecular and turbulent transport implies that

the eddy viscosity (or diffusivity) is described by v

 vl, where v

and l are the velocity and size of the unresolved eddies. Although this

analogy is conceptually appealing, it has several serious shortcomings.

One of these is a lack of separation between the scale of the turbulent

transport and the scale of the resolved motions. Normally, the distinc-

tion between the turbulent and resolved scales is imposed by the

choice of grid spacing in the numerical calculations. Near the scale

of truncation the resolved and unresolved scales are comparable, so

the analogy breaks down. Interactions between the resolved and unre-

solved scales are liable to depend on their relative size, so the effective

viscosity would need to vary with the scale of the resolved flow in

order to reproduce the effect of interactions between the turbulent

and resolved flows.

Another challenge for eddy diffusion models in the geodynamo pro-

blem arises from the anisotropic structure of small-scale convection

(Braginsky and Metlyis, 1990). Eddies are expected to have longer

dimensions in the directions of the rotation axis V and the local

magnetic field B, and a much shorter dimension in the perpendicular

direction (e.g., V  B). Expectations about the magnitude of the eddy

diffusivity (e.g., v

 vl) could be extended from a scalar quantity to a

tensor using information about the dimensions of the eddies in the

three defining directions. However, such an approach would require

substantial effort because the size and orientation of eddies may

change as B evolves. Moreover, the eddies may not be characterized

by a single size or shape. It is more likely that eddies exist over a

broad range of scales. The absence of any clear separation between

the scale of the eddies and the smallest resolved flows returns us to

the problem of requiring the eddy viscosity to vary with the scale

of the resolved flow. The most comprehensive attempt to include the

effects of anisotropic diffusion in geodynamo models is described in

a series of papers by Phillips and Ivers (2000, 2001, 2003).

A variant of the eddy diffusion model replaces the derivatives in the

dissipative terms with higher-order operators. This approach is called

hyperdiffusion because it enhances the damping of motion or the dif-

fusion of heat as the length scale decreases. Hyperdiffusion addresses

the need to make the eddy diffusivity dependent on the scale of the flow.

However, the imposed dependence is usually ad hoc. One approach to

hyperdiffusion replaces the Laplacian operator r

with r

or r

which is equivalent to making the eddy diffusion depend on the wave-

number of the motion in the spectral domain. On the other hand, adding

higher order derivatives introduces the problem of requiring additional

boundary conditions to solve the problem. Most implementations of

hyperdiffusion in geodynamo models alter only the horizontal part

of r

in spherical coordinates, so that the order of the equations for

the radial part of the solution is unchanged (and the number of boundary

conditions is unchanged). This means that turbulent diffusion is handled

differently in the horizontal and radial directions (Grote et al., 2000).

An unintended anisotropy may arise from this implementation of hyper-

diffusivity, which is unrelated to the effects of rotation and large-scale

magnetic fields.

Eddy diffusion and hyperdiffusion models are computationally sim-

ple, but they do a poor job of representing the effects of small-scale

turbulence in magnetoconvection calculations (Buffett, 2003). Several

alternative strategies have developed in recent years for other applica-

tions (see Lesieur and Metais, 1996; Meneveau and Katz, 2000 for

recent reviews). Of particular interest is the scale-similarity model,

and its variants, because these models have the potential to reproduce

the anisotropy of core turbulence. These approaches have grown out of

a conceptual framework known as large-eddy simulations. This frame-

work is useful because it defines the modifications to the governing

equations when the fields are not resolved. Unfortunately, it does not

specify how these additional terms should be evaluated. Another pro-

mising approach, based on Lagrangian averaging, is briefly described

in the concluding remarks.

Large-Eddy simulations

Large-eddy simulations use spatial filtering to eliminate scales that are

smaller than the grid spacing D. Each field in the calculation (velocity

V, for example) is convolved with a filter function G(x) to define the

large-scale fields, e.g.,

Vðx; tÞ¼

ðx  x

ÞVðx

Þdx

(Eq. 2)

Analogous expressions define the large-scale temperature

T and mag-

netic field

B. Applying the filter to the governing equations yields a set

of equations for the large-scale fields. To illustrate, we filter the energy

equation for an incompressible fluid

þrðVTÞ¼kr

T (Eq. 3)

to obtain

]

þrð

TÞ¼kr

T rI

; (Eq. 4)

where

T 

T (Eq. 5)

is the subgrid-scale (SGS) heat flux; I

represents a correction for the

omitted correlations between V and T when the large-scale heat flux is

calculated from

T instead of

T. Other SGS terms arise from the

other nonlinear terms in the relevant governing equations. For the pro-

blem of convection in the Earth’s core, these additional terms include

102 CORE TURBULENCE

the SGS momentum flux (or Reynolds stress), the SGS Maxwell stress

and the SGS induction term (see Buffett, 2003 for details).

The scale-similarity model makes a direct attempt to estimate (5)

using only the resolved part of the fields (Bardina et al., 1980; also

see Leonard, 1974). Suppose that we filter the complete (and

unknown) fields T and V using a wider filter, say G

ðxÞ, to define

the fields

T and V. It follows that the SGS heat flux on the coarser grid

(with resolution 2D) is defined by

¼ V

T  V

T (Eq. 6)

When the amplitude of the fields with scales between 2D and D are

large compared with the amplitudes at scales below D, we can approx-

imate V

and T in Eq. (6) using

and

T . This substitution yields

an approximation for I

. The scale-similarity method supposes that

is similar to I

. Specifically, the spatial pattern is the same,

but the amplitude may differ. The modeled SGS heat flux becomes

[Germano, 1986]

¼ Cð

T 

TÞ (Eq. 7)

where the constant C is used to adjust the amplitude of I

. Automated

procedures for evaluating the model constants have been devised by

Germano et al. (1991). Implementation of this general scheme for a

variant of the scale-similarity method (known as the nonlinear gradient

method) yields model constants C that are typically closed to unity in

both magnetoconvection and plane-layer dynamo calculations (Matsui

and Buffett, 2005). These results are consistent with conclusions

drawn previously by comparing I

and I

using fully resolved calcu-

lations (Buffett, 2003; Matsushima, 2004). A number of technical

challenges remain to be solved to deal with the effects of boundaries

and nonuniform grid spacing. However, the scale-similarity method

provides a framework for making progress in modeling the effects of

core turbulence.

Other approaches and considerations

Another method for dealing with resolved motions in numerical simu-

lations is based on Lagrangian averages of fluid parcel trajectories

(Holm, 2002). The derivation of the governing equations (known as

the alpha model) is based on a variational description of ideal fluid

motion (Chen et al., 1999). The current version of the alpha models

uses a closure based on Taylor’s hypothesis for frozen-in turbulence,

although more elaborate descriptions of the small-scale fluctuations

could be used, in principle. Extensions of the model to include dissipa-

tive effects have been developed using a filtered form of Kelvin’s cir-

culation theorem (Foias et al., 2001) and the results have been cast in

the form of an LES model (Montgomery and Pouquet, 2002), even

though the underlying derivation is fundamentally different. These

recent developments offer promising new lines of investigation for

the study of core turbulence. It is too early to know whether any of

these methods will find widespread use in geodynamo models.

Computational considerations will also govern the choice of suitable

turbulence models. The most viable models must be adaptable to compu-

tational schemes that can exploit massively parallel computers. Almost

all of the existing geodynamo models rely on a spectral expansion of

the fields in spherical harmonics. This approach is ideally suited for

determining the potential field outside of the core. However, it is poorly

suited for parallel computing. The use of spherical harmonics requires

excessive communication between processors, and this problem

becomes more acute as the number of processors increases. Increasing

availability of massively parallel computers has motivated a shift in

attention to other methods of solution that are more efficient for parallel

computations. New dynamo models based on finite elements (Chan

et al., 2001; Matsui and Okuda, 2004), finite differences (Kageyama

and Sato, 2004), and spectral elements (Fournier et al., 2004) are now

in various stages of development. One or more of these methods may

become the future standard. The choice of turbulence models should

be guided by these recent trends because the success of turbulence

models is often dependent on the method of solution (Meneveau and

Katz, 2000).

Bruce Buffett and Hiroaki Matsui

Bibliography

Bardina, J., Ferziger, J.H., and Reynolds, W.C., 1980. Improved sub-

grid scale models for large-eddy simulations. American Institute

of Aeuronautics and Acoustics Journal, 34: 1111–1119.

Braginsky, S.I., and Meytlis, V.P., 1990. Local turbulence in the

Earth’s core. Geophysical and Astrophysical Fluid Dynamics, 55:

71–87.

Buffett, B.A., 2003. A comparison of subgrid-scale models for large-

eddy simulations of convection in the Earth’s core. Geophysics

Journal International, 153: 753–765.

Buffett, B.A., and Bloxham, J., 2002. Energetics of numerical geody-

namo models. Geophysical Journal International, 149:211–221.

Chan, K.H., Zhang, K., Zou, J., and Schubert, G., 2001. A nonlinear

3-D spherical a

dynamo using a finite element method. Physical

Earth Planet Interiors, 128:35–50.

Chen, S., Foias, C., Holm, D.D., Olson, E., Titi, E.S., and Wynne, S.,

1999. A connection between the Camassa-Holm equations and

turbulent flow in pipes and channels. Physics of Fluids, 11:

2343–2353.

Christensen, U., Olson, P., and Glatzmaier, G.A., 1998. A dynamo

interpretation of geomagnetic field structures. Geophysical

Research Letters, 25: 1565–1568.

Christensen, U., Olson, P., and Glatzmaier, G.A., 1999. Numerical

modeling of the geodynamo: A systematic parameter study. Geo-

physics Journal International, 138: 393–409.

Clune, T.C., Elliott, J.R., Miesh, M.S., Toomre, J., and Glatzmaier,

G.A., 1999. Computational aspects of a code to study rotating

turbulent convection in spherical shells. Parallel Computing, 25:

361–380.

Dobson, D.P., 2000. Fe-57 and Co tracer diffusion in liquid Fe-FeS at

2 and 5 GPa. Physics of the Earth and Planetary Interiors, 120:

137–144.

Foias, C., Holm, D.D., and Titi, E.S., 2001. The Navier-Stokes-alpha

model of fluid turbulence. Physica D, 152: 505–519.

Germano, M., 1986. A proposal for a redefinition of the turbulent

stresses in the filtered Navier-Stokes equations. Physics of Fluids,

29: 2323–2324.

Germano, M., Piomelli, U., Moin, P., and Cabot, W.H., 1991. A

dynamic subgrid-scale eddy viscosity model. Physics of Fluids A,

3: 1760–1765.

Glatzmaier, G.A., and Roberts, P.H., 1995. A three-dimensional

convective dynamo solution with rotating and finitely conducting inner

core and mantle. Physics of Earth and Planetary Interiors, 91:63–75.

Glatzmaier, G.A., and Roberts, P.H., 1996. An anelastic evolutionary

geodynamo simulation driven by compositional and thermal buoy-

ancy. Physica D, 97:81–94.

Grote, E., Busse, F.H., and Tilgner, A., 1999. Convection-driven quad-

rupolar dynamos in rotating spherical shells. Physical Review E,

60: R5025–

R5028.

Grote, E., Busse, F.H., and Tilgner, A., 2000. Effects of hyperdiffusiv-

ities on dynamo simulations. Geophysical Research Letters, 27:

2001–2004.

Hollerbach, R., 2003. The range of timescales on which the geody-

namo operates. In Dehant, V., et al., (ed.), Earth’s Core: Dynamics,

Structure, Rotation. Geodynamics Monograph, American Geophy-

sical Union, Vol. 31, 181–192.

Holm, D.D., 2002. Lagrangian averages, averaged Lagrangians and the

mean effect of fluctuations in fluid dynamics. Chaos, 12:518–530.

CORE TURBULENCE 103

Kageyama, A., and Sato, T., 1995. The Complexity Simulation Group,

Computer simulation of a magnetohydrodynamic dynamo. Physics

of Plasmas, 2: 1421–1431.

Kageyama, A., and Sato, T., 1997. Generation mechanism of a dipole

field by a magnetohydrodynamic dynamo. Physical Review Letters

E, 55: 4617–4626.

Kageyama, A., and Sato, T., 2004. Yin-Yang grid: An overset grid in

spherical geometry. Geochemistry, Geophysics, and Geosystems,

5, Q09005.

Katayama, J.S., Matsushima, M., and Honkura, Y., 1999. Some char-

acteristics of magnetic field behavior in a model of MHD dynamo

thermally driven in a rotating spherical shell. Physics of Earth and

Planetary Interiors, 111: 141–159.

Kono, M., Sakuraba, A., and Ishida, M., 2000. Dynamo simulation

and paleosecular variati on models. Philosophical Transactions of

the Royal Society of London, A358: 1123–1139.

Kuang, W., and Bloxham, J., 1997. An Earth-like numerical dynamo

model. Nature, 389: 371–374.

Landau, L.D., and Lifshitz, E.M., 1981. Physical Kinetics, Course of

Theoretical Physics, Vol. 10, Oxford: Pergamon Press.

Leonard, A., 1974. Energy cascade in large-eddy simulations of turbu-

lent flow. Advances In Geophysics, 18: 237–248.

Lesieur, M., and Metais, O., 1996. New trends in large-eddy simula-

tions of turbulence. Annual Review of Fluid Mechanics, 28:45–82.

Matsui, H., and Okuda, H., 2004. Development of a simulation code

for MHD dynamo processes using the GEOFEM platform. Interna-

tional Journal of Computational Fluid Dynamics, 18: 323–332.

Matsui, H., and Buffett, B.A., 2005. Subgrid-scale modeling of con-

vection-driven dynamos in a rotating plane layer. Physics of Earth

and Planetary Interiors, 153: 108–123.

Matsushima, M., Nakajima, T., and Roberts, P.H., 1999. The aniso-

tropy of local turbulence in the Earth’s core. Earth, Planets and

Space, 51: 277–286.

Matsushima, M., 2004. Scale similarity of MHD turbulence in the

Earth’s core. Earth, Planets, Space, 56: 599–605.

McFadden, P.L., and Merrill, R.T., 2000. Evolution of the geomagnetic

reversal rate since 160 Ma: Is the process continuous? Journal of

Geophysical Research, 105: 28455–28460.

Meneveau, C., and Katz, J., 2000. Scale invariance and turbulence

models for large-eddy simulation. Annual Review of Fluid

Mechanics, 32:1–32.

Moffatt, H.K., 1978. Magnetic Field Generation in Electrically Con-

ducting Fluids, Cambridge, UK: Cambridge University Press,

343 pp.

Montgomery, D.C., and Pouquet, A., 2002. An alternative interpreta-

tion for the Holm alpha model. Physics of Fluids, 14: 3365–3566.

Olson, P., Christensen, U., and Glatzmaier, G.A., 1999. Numerical

modeling of the geodynamo: Mechanisms of field generation

and equilibration. Journal of Geophysical Research, 104:

10383–10404.

Phillips, C.G., and Ivers, D.J., 2000. Spherical anisotropic diffusion

models for the Earth’s core. Physics of Earth and Planetary Inter-

iors, 117: 209–223.

Phillips, C.G., and Ivers, D.J., 2001. Spectral interactions of rapidly

rotating anisotropic turbulent viscous and thermal diffusion in

the Earth’s core. Physics of Earth and Planetary Interiors, 128:

93–107.

Phillips, C.G., and Ivers, D.J., 2003. Strong-field anisotropic diffusion

models for the Earth’s core. Physics of Earth and Planetary Inter-

iors, 140:13–28.

Piomelli, U., and Zang, T.A., 1991. Large-eddy simulation of transitional

channel flow. Computer Physics Communications, 65:224–230.

Roberts, P.H., and Glatzmaier, G.A., 2000a. Geodynamo theory and

simulations. Reviews of Modern Physics, 72: 1081–1123.

Shimizu, H., and Loper, D.E., 1997. Time and length scales of

buoyancy-driven flow structures in a rotating hydromagnetic fluid.

Physics of Earth and Planetary Interiors, 104: 307–329.

St. Pierre, M.G., 1996. On the local nature of turbulence in Earth’s

outer core. Geophysical and Astrophysical Fluid Dynamics, 83:

293–306.

Tennekes H., and Lumley, J.L., 1972. A First Course in Turbulence,

Cambridge, MA: The MIT Press.

Vocadlo, L., Alfe, D., Price, G.D., and Gillan, M.J., 2000. First-

principle calculations of the diffusivity and viscosity of liquid

Fe-FeS at experimentally accessible conditions. Physics of Earth

and Planet. Interiors, 120: 145–152.

Zhang, K.K., 1994. On the coupling between Poincare equation and

the heat equation. Journal of Fluid Mechanics, 268:211–229.

CORE VISCOSITY

Definition of viscosity

The transport properties of fluid materials (either solid or liquid) are

determined by their viscosity, which defines the resistance of the mate-

rial to fluid flow (i.e., how “runny” it is). Viscosity, , describes the

time dependence of material motion through the ratio of applied shear

stress, s, to strain rate,

e via

 ¼

(Eq. 1)

The Earth’s liquid outer core will have a relatively low viscosity com-

pared to that of the solid inner core, which deforms on a much longer

timescale. In geophysics, the quantity  is referred to as the dynamic

viscosity, which, when normalized by the density, r, is termed the

kinematic viscosity, n:

n ¼



(Eq. 2)

Viscosity is a quantity dependent on the properties of the fluid at a

molecular level. Therefore, both the viscosities defined above may also

be referred to as “molecular viscosity.” In the outer core, fluid motion

occurs over a range of length scales from that at a molecular level to

large-scale motion with characteristic distances comparable with the

outer core radius. Such large-scale motion does not exist in isolation,

but has embedded within it turbulence over a range of length scales,

which serve to drain the largest scale flow of its energy. Consequently,

this energy dissipation causes an increase in the viscosity of the large-

scale fluid, resulting in an “effective viscosity” or “turbulent viscosity”

of a much larger magnitude than the molecular viscosity defined

earlier. This effective viscosity has been observed experimentally in

turbulent fluids yet it is very difficult to quantify and impossible to

derive rigorously; however estimates for effective viscosities are often

used when modeling the outer core. Viscosity is a very important para-

meter in geophysics since the viscosity of materials in the Earth’s core

are a contributory factor in determining overall properties of the core

itself, such as core convection (see Core properties and Core convec-

tion); indeed, the fundamental equations governing the dynamics of

the outer core and the generation and sustention of the magnetic field

are dependent, in part, on the viscosity of the outer core fluid.

Quantifying outer core viscosity

There have been many estimates made for outer core viscosity derived

from geodetic, seismological, geomagnetic, experimental, and theoreti-

cal studies. However, the values so obtained span 14 orders of magnitude

(see Secco, 1995).

Geodetic observations (e.g., free oscillations, the Chandler wobble,

length of day variations, nutation of the Earth, tidal measurements,

gravimetry) lead to viscosity estimates ranging from 10 mPa s (observa-

tions of the Chandler wobble, Verhoogen, 1974) to 10

mPa s (analysis

104 CORE VISCOSITY

of free oscillation data, Sato and Espinosa, 1967). Theoretical geodetic

studies (e.g., viscous coupling of the core and mantle, theory of rotating

fluids, inner core oscillation ( q.v. ), core nutation) lead to viscosity esti-

mates ranging from 10 mPa s (evaluation of decay time of inner core

oscillation ( q.v. ), Won and Kuo, 1973) to 10

mPa s (secular decelera-

tion of the core by viscous couplin g, Bondi and Lyttleton, 1948). Gener-

ally much higher values for viscosity (10

– 10

mPa s) are obtained

from seismological observations of the attenuation of P- and S-waves

through the core (e.g., Sato and Espinosa, 1967; Jeffreys, 1959), and

from geomagnetic data (e.g., 10

mPa s; Officer, 1986).

The viscosities of core-forming materials may also be determined

experimentally in the laboratory and theoretically through computer

simulation. Empirically, viscosity follows an Ahrrenius relation of

the form (see Poirier, 2002):

/ exp



(Eq. 3)

where Q

is the activation energy. Poirier (1988) analyzed data for a

number of liquid metals and found that there is also an empirical rela-

tion between Q

and the melting temperature:

ﬃ 2 :6 RT

(Eq. 4)

This very important result implies that the viscosity of liquid metals

remains constant (i.e., independent of pressure) along the melting

curve and therefore equal to that at the melting point at ambient pres-

sure, which is generally of the order of a few mPa s. Furthermore,

Poirier went on to state that the viscosity of liquid iron in the outer

core would, therefore, be equal to that at ambient pressure ( 6 mPa s).

On a microscopic level, an approximation for the viscosity of liquid

metals is given by the Stokes-Einstein equation, which provides a

relationship between diffusion and viscosity of the form:

D ¼

2 pa

(Eq. 5)

where a is an atomic diameter, T is the temperature, k

is the Boltz-

mann constant, and D is the diffusion coefficient.

Theoretical values for diffusion coefficients have been obtained

from ab initio molecular dynamics simulations on liquid iron at core

conditions (de Wijs et al. , 1998), leading to a predicted viscosity of

12 –15 mPa s using the Stokes-Einstein relation above. However,

although the Stokes-Einstein equation has proved successful in estab-

lishing a link between viscosity and diffusion for a number of mona-

tomic liquids, it is not necessarily the case that it should be effective

for alloys or at high pressures and temperatures. To address the valid-

ity of the Stokes-Einstein relation and to assess the effect of impurities

on viscosity coefficients, a number of experimental and theoretical stu-

dies have been performed on the Fe-FeS system. High-pressure tracer

diffusion experiments (Dobson et al. , 2001) have been carried out

on liquid Fe-FeS alloys at 5 GPa, resulting in high diffusivities

(10

–5

1

) in excellent agreement with ab initio molecular

dynamics calculations performed at the same conditions (Vo čadlo

et al. , 2000). When incorporated into Eq. 5, these diffusiviti es lead

to values for viscosity of a few mPa s.

Direct viscosity measurements (Dobson et al., 2000) of Fe-FeS

alloys by means of the falling-sphere technique have been made at

similar pressures and temperatures to those used in the diffusion

experiments above; these resulted in values for viscosities in excel-

lent agreement with those derived experimentally using the Stokes-

Einstein relation. Furthermore these results are in excellent agreement

with ab initio molecular dynamics calcula tions of viscosity based on

rigorous Green-Kubo functions of the stresses obtained directly from

the simulations (Vo čadlo et al. , 2000). All of these results thus provide

both experimental and theoretical verification of the Stokes-Einstein

relation (Eq. 5).

The results from these studies further show not only that the viscos-

ity of liquid iron at core pressures is approximately equal to that at low

pressures, verifying Poirier ’s groundbreaking and insightful result

(Poirier, 1988), but also that the introduction of light elements into

Fe liquid does not appear significantly to effect the values. Both

ab initio calculations and experimen ts consistently give viscosities of

the order of a few mPa s. This suggests that viscosity changes little

with homologous temperature, and it is now generally accepted that

the viscosity of the outer core is likely to be a few mPa s (comparable

to that of water on the Earth ’s surface).

In general, viscosities derived from Earth observations are high

(10

– 10

mPa s) and those based on laboratory experiments and the-

oretical considerations are much lower (1 – 10 mPa s). The disparate

values for viscosity arise for two main reasons: the type of viscosity

being measured (molecular or effective) and the large uncertainties

associated with the interpretation of Earth observation data. It is also

possible that viscosity measurements made from the direct observa-

tions of the Earth are not actually measuring viscosity at all, but some

other effects that are being attributed to viscosity; this would certainly

be the case if the “true ” viscosity were of the order of mPa s, since

such a small viscosity is unlikely to be detectable.

A low viscosity leads to viscous forces that are essent ially negligible

when compared to the Coriolis force, supporting the view of an outer

core in a state of small-circulation turbulent convection rather than a

more coherent pattern of convection on a much larger scale compar-

able with the core radius. If this is the case, it is necessary to obtain

accurate values for viscosity in order to quantify this turbulence in

the outer core.

Viscos ity and the inner core

The inner core is not perfectly elastic and has a finite viscosity with

deformation occurring over long timescales. Placing numerical con-

straints on the viscosity of the inner core is fundamental to understand-

ing important core processes such as differential inner core rotation

( q.v. ), inner core oscillation (q.v. ), and inner core anisotropy (q.v. ) (see

Bloxham, 1988).

High-temperature experiments on solid iron at ambient pressure lead

to estimates for viscosities of 10

Pa s (Frost and Ashby, 1982);

however, this is likely to be a lower limit as the value may increase

at higher pressures. Seismological and geodetic observations have

led to a number of estimates for inner core viscosity ranging from

to 10

Pa s (see Dumberry and Bloxham, 2002). In particular,

Buffett (1997) modeled the viscous relaxation of the inner core by

calculating the relaxation time for the inner core to adjust, as it rotates,

back to its equilibrium shape after small distortions due to perturba-

tions in gravitational potential imposed by the overlying mantle. He

suggested that the viscosity has to be constrained to be either less than

Pa s (if the whole inner core is involved in the relaxation) or greater

than 10

Pa s (if there is no relaxation of the inner core), although this

latter case may lead to gravitational locking and hence no differential

rotation.

Quantifying the viscosity of the phases present in the inner core at a

microscopic level is a very difficult problem. At temperatures close to

the melting point (as expected in the inner core) viscous flow is likely

to be determined either by dislocation creep (Harper-Dorn creep) or

diffusion creep (Nabarro-Herring creep).

The overall viscosity of inner core material has diffusion-driven and

dislocation-driven contributions:

 ¼



diff





disl



1

(Eq. 6)

CORE VISCOSITY 105