Гриффитс Дж. Научные методы исследования осадочных пород

Подождите немного. Документ загружается.

172

ГЛАВА 10

винными, изучались лишь акцессории рыхлых пород, например морских

и аллювиальных песков [86]. Интерес к ним не был чисто академическим,

так как среди этих минералов иногда находили драгоценные камни. Согласно

Босуэллу [36], примерно до 1870 г. аналитическая методика ориентирова-

лась в основном на химические анализы, но уже в это время пользовались

магнитной сепарацией и диагностикой минералов по кристаллографическим,

формам. После 1870 г. стали широко применять разделение минералов в тяже-

лых жидкостях. Были разработаны стандартные процедуры для получения

«тяжелых» концентратов из пород. В период с 1870 по 1890 г. при петрогра-

фических исследованиях начали применять поляризационный микроскоп,

благодаря чему этот период нужно считать кульминационным для описа-

тельной петрографии. Выдающимся примером исследований «тяжелых»

минералов была работа Туле [425] по пескам Сахары.

Интерес к акцессорным минералам возрос в течение последнего деся-

тилетия прошлого века. В этот период была разработана более совершенная

методика, появились и более детальные исследования; здесь следует ука-

зать на работы Ретджерса [348], который первым поставил· вопрос о воз-

можности определения областей сноса и условий осадконакопления

по результатам изучения акцессорных минералов. Артини [16] предложил

ввести количественную оценку содержания акцессориев в породе с помощью

шкалы с показаниями от 1 до 10 (т. е. от широко распространенных до редко

встречаемых). В это же время в своей классической работе Кайе [53] рас-

сматривал вопрос об акцессорных минералах карбонатных пород.

Периодом расцвета исследований акцессорных минералов и становления

их как самостоятельной научной дисциплины, преподаваемой в университе-

тах [36, стр. 25], можно считать 1900—1920 гг.

Акцессорные минералы стали обнаруживать во все более и более древ-

них породах. Был выработан основной принцип, согласно которому каждому

типу осадочных пород присущ характерный, только ему свойственный ком-

плекс акцессорных минералов. После этого стало возможным проводить

стратиграфические корреляции с помощью тяжелых минералов [33]. Иллингс

[210], коллега Босуэлла, впервые применил анализ акцессорных минералов

в нефтяной геологии, когда он скоррелировал третичные отложения Три-

нидада

Уже давно было установлено, что комплекс тяжелых минералов, содер-

жащихся в какой-либо осадочной породе, можно отнести к той или иной

области сноса, если известны тяжелые минералы пород, слагающих эту

область. Рэсталл и Уилкоксон [345] были одними из первых исследователей,

пытавшихся описать акцессорные минералы изверженных пород. Макки

[284], изучая модификации кварца, предложил использовать разновидности

минералов, что было усовершенствовано Браммаллом [37] в его известном

исследовании дартмурских гранитов. Так как Гровс [182] знал комплекс

тяжелых минералов в этих гранитах и в породах соседних участков, пред-

ставленных также гранитами, ему удалось оценить степень участия различ-

ного гранитного материала в формировании кайнозойских осадочных пород

Южной Англии.

Таким образом, к началу 30-х годов нашего века были канонизированы

основные особенности исследований акцессорного состава. Было установ-

лено также [36, стр. 47—49], что результаты исследований можно применять

для нахождения областей сноса, выяснения условий транспортировки и седи-

ментации, а также, на основании относительной стабильности различных

минеральных видов, введения диагенеза. В течение двух следующих деся-

тилетий (1920—1940 гг.) изучение акцессорных минералов было признано

Название «Тринидад» повсюду в книге относится к одному из островов бывшей

британской Вест-Индии, который ныне является частью страны, называемой «Тринидад

и Тобаго».

АКЦЕССОРНЫЕ МИНЕРАЛЫ

173

в качестве стандартного метода в нефтяной геологии, причем большая эффек-

тивность метода была продемонстрирована при многих обширных иссле-

дованиях; особенно эффективно оказалось изучение третичных осадочных

пород [95, 97, 105, 117, 194, 347].

К началу 1940-х годов стало очевидным, что если для палеогеографиче-

ских реконструкций обширных областей и корреляций стратиграфических

подразделений в широких пределах изучение акцессорных минералов при-

носит несомненную пользу, то эффективность этого метода при детальных

исследованиях оказалась сомнительной, так как локальные отклонения

часто бывают слишком значительными, затушевывающими основные зако-

номерности. Уже давно было установлено, что содержание акцессорных

минералов в осадочных породах может изменяться в зависимости от селек-

тивной сортировки [36, стр. 5, 75 и ниже]. Одним из первых роль этого

фактора подчеркнул Руби [371]. Пытались снять влияние эффекта сорти-

ровки на размеры путем изучения зерен, принадлежащих к одному или

двум классам размеров [376], но эти попытки оказались малоэффективными.

Природа этой проблемы и ее значительность были окончательно выяснены

и описаны Риттенхаусом [358, 359]. В своих работах он отмечал существен-

ные ограничения в использовании изменчивости относительных содержаний

акцессорных минералов. Их изучение продолжалось и в 40-х годах и позже,

однако уже без прежнего энтузиазма — решались лишь определенные спе-

цифические проблемы [11, 209].

Очевидно, что достижение более точных и конкретных выводов требует

более строгого подхода к проблеме, такого подхода, с помощью которого

можно было бы «извлекать определенный сигнал из беспорядочного шума»,

т. е. изучать все

более и более тонкие колебания относительных содержаний

акцессорных минералов.

10.3. ОПРЕДЕЛЕНИЕ КЛАССОВ ЭЛЕМЕНТОВ

Акцессорные минералы обычно классифицируются в гомогенные группы

с помощью определенного набора диагенетических критериев. Во многих

справочниках можно найти очень сложные наборы критериев, по которым

определяются минералы [248, 300, 455]. Можно рекомендовать таблицы,

например такие, как в книгах А. Винчелла и Г. Винчелла [455, табл. 3]

или Рассела [379]. Следует, однако, признать, что диагностика акцессорных

минералов представляется особым искусством, приобретаемым в основном

в результате длительной практики. Так же как и в обычном минералоги-

ческом анализе, процедура диагностики требует соблюдения некоторых пси-

хофизических предпосылок для постепенного приобретения определенных

навыков. Для новичка эта процедура представляется обычно наиболее труд-

ной сравнительно с другими подобными работами. Акцессорные минералы

гораздо труднее определять в свободных зернах, чем в шлифах, так как

кроме изменений, обнаруживаемых в шлифах, свободные зерна меняются

по своим размерам и габитусу. Поэтому наиболее верным диагностическим

критерием минерала является его облик, или габитус

. В сознании любого

специалиста, опытного в диагностике тяжелых минералов, каждый минерал

имеет определенный облик. Такой специалист интуитивно улавливает черты

сходства в кристаллах, отличающихся по некоторым специфическим осо-

бенностям габитуса. В шлифах сечения зерен всегда произвольны и случай-

ны. Приготавливая препараты с цельными зернами, минералоги наблюдают

свободные зерна в каком-либо стабильном положении, обычно в таком, кото-

рое обеспечивает максимальную площадь проекции. Например, в шлифах

Под габитусом кристалла понимаются его естественные очертания и величина

как признаки, которые не меняются при любом способе приготовления изучаемого пре-

парата.

174

ГЛАВА 10

базальный пинакоид мусковита встречается редко, а в свободных зернах

эта грань наблюдается часто. Далее, в шлифах вряд ли можно мусковит

принять за топаз, а в препаратах со свободными зернами тот и другой имеют

вид бесцветных округлых пластинок (базальные пинакоиды) со сходным

рельефом (показатель преломления ±1,64). В шлифах оба минерала кажутся

изотропными, поэтому в сходящемся свете обоим им свойственна двухосная

интерференционная фигура либо с малым, либо с несколько большим углом

между оптическими осями (2V). Таким образом, эти минералы легко при-

нять один за другой. И лишь по единственному признаку их можно отли-

чить — топаз оптически положителен, мусковит — отрицателен.

Триклинныи бесцветный

Грань

а(юо)

VI "

Медленно

1,720

Быстро

Двупреломление=0,008

Фигура оптических

осей - ve

Угол погасания

ZAc—30° t

Грань Ь(ОЮ)

1,728

Грань C(OOl)

1,720

(Z)Y

Медленно

Быстро

1,712

Двупреломление=0,016 Двупреломление - 0,016-0,008

Сечение с наивысшими Погасание прямое

интерференционными

окрасками фигура

оптических осей,

или

Угол погасания

сечение

наивысшими интер-

XAa = 7½°

ференционными

окрасками

Для грани

(110),

так

же

как и для грани (100),ZAcOQ"; фигура

оптических

осей

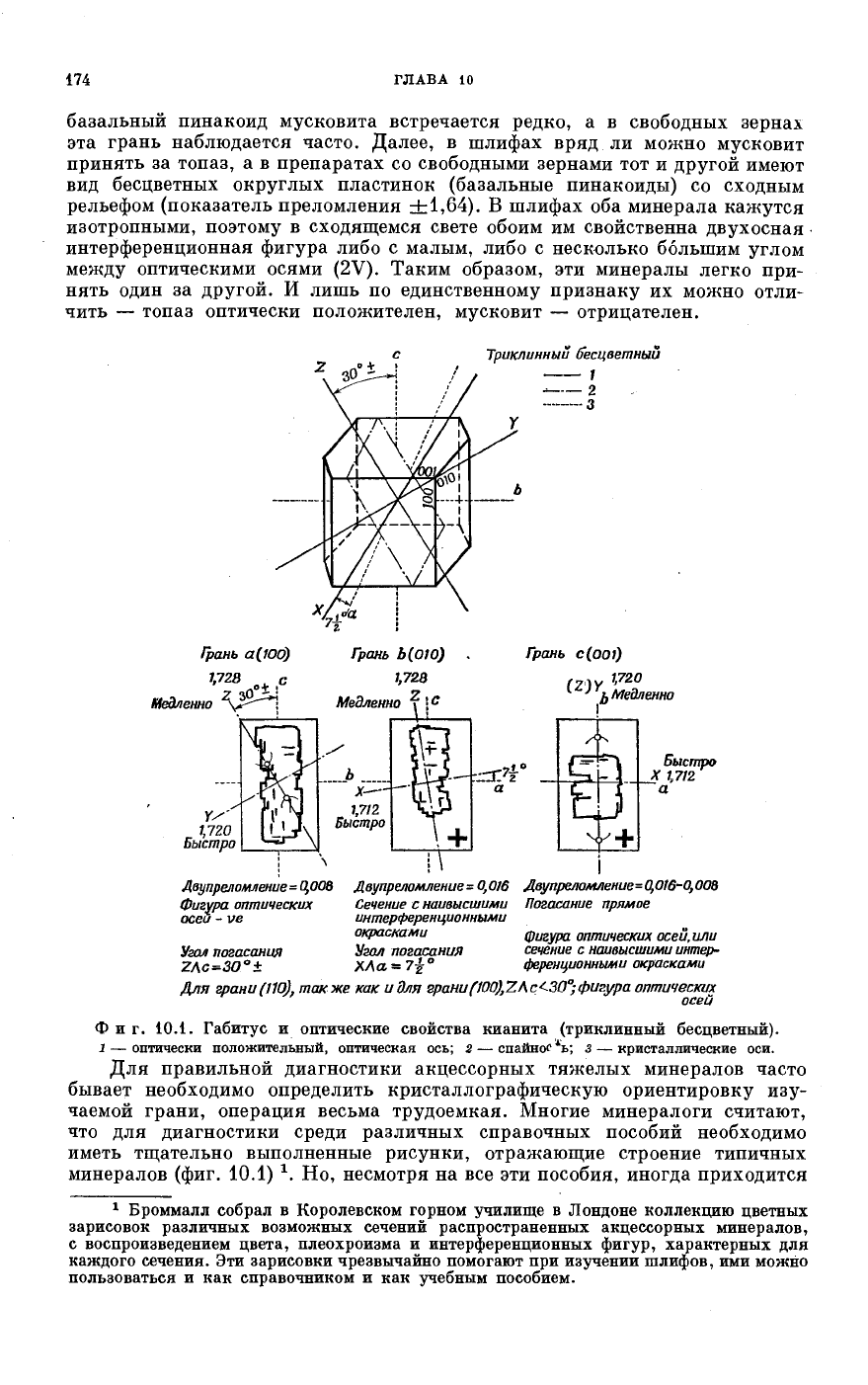
Фиг. 10.1. Габитус и оптические свойства кианита (триклинный бесцветный).

1 — оптически положительный, оптическая ось; 2 — спайное

ъ\ з — кристаллические оси.

Для правильной диагностики акцессорных тяжелых минералов часто

бывает необходимо определить кристаллографическую ориентировку изу-

чаемой грани, операция весьма трудоемкая. Многие минералоги считают,

что для диагностики среди различных справочных пособий необходимо

иметь тщательно выполненные рисунки, отражающие строение типичных

минералов (фиг. 10.1) Но, несмотря на все эти пособия, иногда приходится

Броммалл собрал в Королевском горном училище в Лондоне коллекцию цветных

зарисовок различных возможных сечений распространенных акцессорных минералов,

с воспроизведением цвета, плеохроизма и интерференционных фигур, характерных для

каждого сечения. Эти зарисовки чрезвычайно помогают при изучении шлифов, ими можно

пользоваться и как справочником и как учебным пособием.

АКЦЕССОРНЫЕ МИНЕРАЛЫ

175

извлекать то или иное зерно из препарата и определять его показатель пре-

ломления в иммерсионных жидкостях. Алан Стюарт (университетский кол-

ледж Свенси) продемонстрировал автору несколько иной способ: в покровном

стекле препарата с зернами делают отверстие, бальзам растворяют в кси-

лене, зерно помещают на специально сконструированный столик, вращаю-

щийся в жидкости с известным показателем преломления. Наблюдая зерно

в разных положениях под микроскопом, определяют показатель преломления

и, следовательно, минеральный вид [147].

Одно из преимуществ элементов-примесей перед акцессорными мине-

ралами состоит в том, что определение элементов производится автоматиче-

ски, посредством того или иного механического устройства. В определенных

условиях также автоматически можно оценить относительное содержание

тех или иных элементов. Точность или воспроизводимость результатов диаг-

ностики минералов и оценки их содержания определяется здесь качеством

того или иного устройства. С помощью совершенйых приборов можно про-

анализировать большее количество образцов, сэкономив при этом время

и средства. Кроме того, обучить персонал производить анализ элементов-

примесей гораздо легче, чем определять акцессорные минералы. В силу этих

обстоятельств можно считать, что до тех пор, пока изучение акцессорных

минералов не станет обеспечивать получение какой-то уникальной информа-

ции, имеющей большой интерес и значение, популярность, какой это изуче-

ние пользовалось в 30-х годах нашего века, не вернется.

Грань Ь(ою)

1,696

быстро

Двупрело'мление=0,006

Погасание прямое

Сечение с наивысшими интер-

ференционными окрасками

амедленно

Z 1,702

ои-цоизит

С ; X 1,702 быстро

β -цоизит (железосодержащий)

Плоскость оптических осей OOI

а медленно

Z 1,706

Двупреломление

0,004

Погасание прямое

Фигура оптических осей

Грань C(OOl)

а\ Z 1,734 медленно

Y 1,729

Ь быстро

Двупреломление=0,005

Погасание прямое

Косая фигура оптических осей

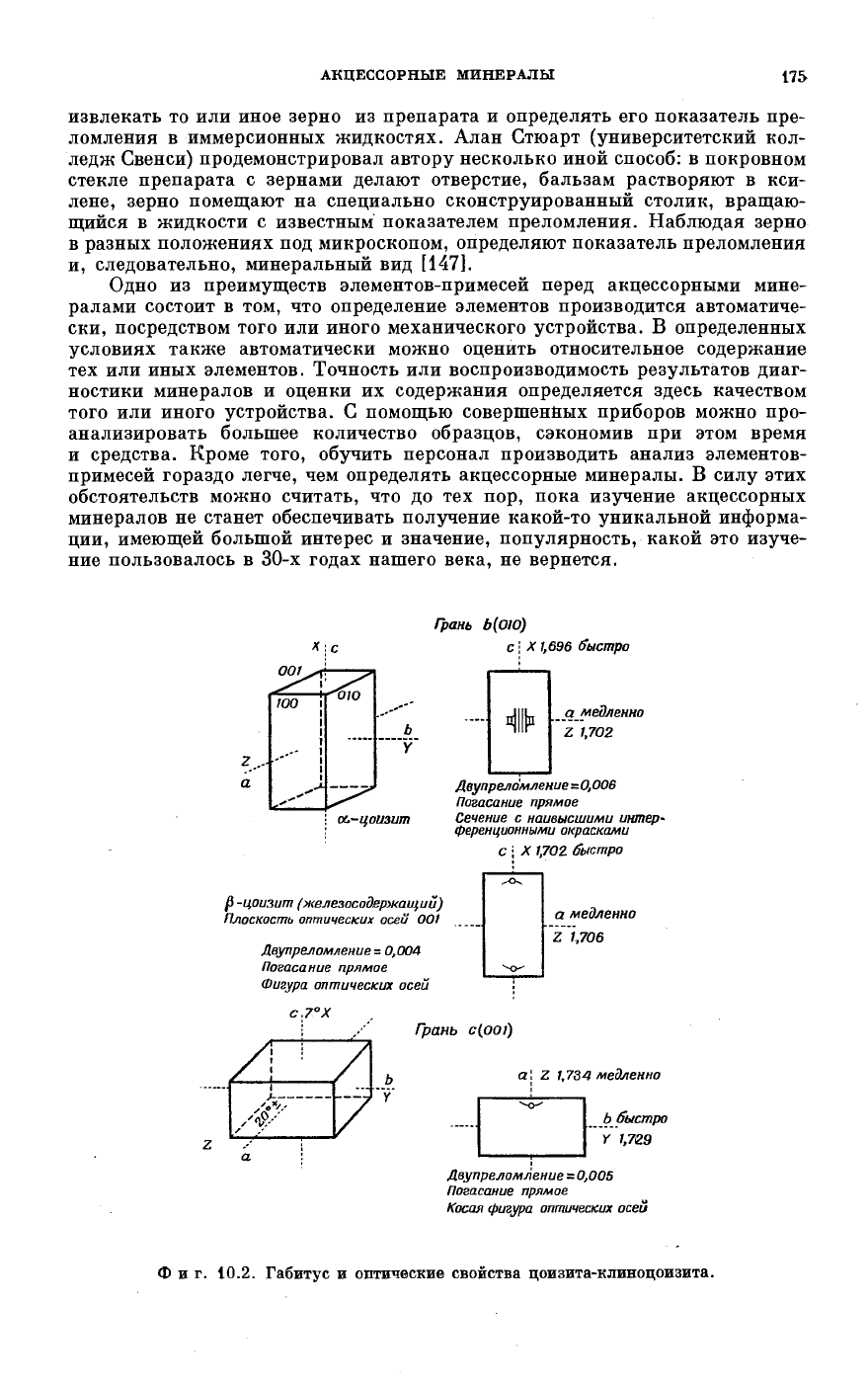
Фиг. 10.2. Габитус и оптические свойства цоизита-клиноцоизита.

176

ГЛАВА 10

10.4. ПОДГОТОВИТЕЛЬНЫЕ ОПЕРАЦИИ И МЕТОДИКА ИЗМЕРЕНИЙ

Сегрегация акцессорных минералов и получение их концентратов,

основаны главным образом на их большей плотности сравнительно с плот-

ностью породообразующих минералов — кварца, полевых шпатов, обломков

пород (отсюда и происходит название «тяжелые минералы»). Прежде всего

необходимо дезинтегрировать образец породы, не нарушая при этом по воз-

можности габитуса тяжелых минералов. Затем дезинтегрированную пробу

опускают в тяжелую жидкость, например в бромоформ или четырехброми-

стый ацетилен. При этом легкие минералы всплывают, а тяжелые опускаются

на дно.

Свойства наиболее широко применяющихся тяжелых жидкостей сведены

в табл. 10.2. Характеристику различных аппаратов для разделения зерен

Таблица 10.2

Тяжелые жидкости для отделения акцессорных минералов

Бромоформ

(трибромметан)

Четырехбромистый

ацетилен (силс.«-тетра-

бромметан-1,1,2 2-тетра-

бромметан)

Йодистый метилен

(дииодметан)

Формула

Молекулярный вес

Точка кипения, °С

Точка замерза-

ния, °С

Плотность

Показатель пре-

ломления

Примечание

CHBr

252,77

149,5

6-7

2,890 (при 20° С)

1,63795 (при 19° С)

Жидкость бесцвет-

ная или гексаго-

нальные кристал-

лы

345,70

151,0

0,1

2,9630 (при 20° С)

1,63795

Жидкость бесцветная

до желтой, разлага-

ется при 239

—

242° С

267,68

180

5-6

3,325 (при 10,5° С)

1,7559 (при 10,5° С)

Жидкость бесцветная,

начало кристалли-

зации при 0° С

Литературный источник. «Руководство по химии и физике», 28-е изд. «Кемикел Раббер Паб-

лишинг Компани», Кливленд, Огайо, 1944.

можно найти в обычных учебных пособиях [248, стр. 335—344; 300, стр. 101

и ниже]. Для анализа небольшого числа проб достаточно собрать простейшее

приспособление, состоящее из двух разделительных воронок и стакана для

сбора излишней жидкости (фиг. 10.3). Если анализу подлежит большое

количество проб и необходимо получить количественные результаты, следует

организовать работу более рационально. В частности, для более полной

и быстрой сеперации и для обеспечения более простого контроля анализа

рекомендуется применять центрифугирование.

Основная трудность при сепарации центрифугой состоит в извлечении

тяжелой фракции. Один из способов извлечения был продемонстрирован

Р. Маккеем в Королевском горном училище в Лондоне (устное сообщение,

1938). Маккей использовал простой сосуд для центрифугирования

(фиг. 10.4, А). После того как сепарация легких и тяжелых элементов была

достигнута, сосуд с бромоформом заморозили в смеси льда и поваренной

соли. Легкое нагревание сосуда в руке позволяет извлечь из сосуда замерз-

ший столбик бромоформа с вмерзшими в него зернами. Затем столбик разби-

вают, и ту его часть, в которой содержатся тяжелые зерна, кладут на филь-

тровальную бумагу в воронку, где бромоформ тает и стекает сквозь фильтр.

Если легкие минералы не представляют интереса, содержащую их часть

столбика собирают в общем контейнере, где их фильтруют. Для точных

количественных исследований подобная методика неудовлетворительна, так

АКЦЕССОРНЫЕ МИНЕРАЛЫ 177

как при извлечении столбика из сосуда часть легкой фракции иногда прили-

пает к стенкам сосуда и загрязняет тяжелую фракцию. Усовершенствование,

предложенное Крыниным (устное сообщение, 1947), состоит в том, что нижняя

часть сосуда должна быть резко суженной (фиг. 10.4, Б), что обеспечивает

замораживание жидкости лишь в этой нижней узкой части сосуда. Затем

легкую фракцию вместе с бромоформом удаляют из сосуда и промывают.

Далее извлекают тяжелую фракцию. По альтернативной методике, впервые

предложенной Салливаном [420] и независимо от него разработанной Джеф-

фрисом [218], внутри основного сосуда для центрифугирования помещают

специальный сосуд по способу, показанному на фиг. 10.4, В. Пробу поме-

щают во внутренний сосуд. После центрифугирования верхнее отверстие

Легкая

фракция

Легкая

фракция

•

Фиг. 10.3. Аппарат для сепарации

тяжелых минералов с помощью тяжелых

жидкостей.

1 — фильтровальная воронка; г— легкие ми-

нералы; 3 — тяжелая жидкость; 4 — тяжелые

минералы; 5 — зажим; в — фильтровальная

воронка; 7 — фильтр; 8— тяжелые минералы;

9 — излишек тяжелой жидкости в стакане.

Тяжелая фракция (^vJ Тяжелая фракция

А Б В

Фиг. 10.4. Сосуды для сепарации тяжелых

минералов в тяжелых жидкостях с помощью

центрифугирования,

А — замораживание всего содержимого сосуда (устное

сообщение Р. А. Макеея, 1938); Б — замораживание

только суженной, нижней части сосуда (устное сообще-

ние Крынина, 1947); В — сосуд в сосуде [212].

внутреннего сосуда закрывают рукой, и остающаяся в нем легкая фракция

отделяется от тяжелой. Последняя находится во внешнем сосуде, откуда ее

отфильтровыв ают.

При центрифугировании бромоформа или любой другой тяжелой жидко-

сти возникает одно техническое затруднение: под воздействием веса тяже-

лой жидкости во время операции сосуд лопается. Чтобы этого избежать,

надо поместить стеклянный сосуд вместе с его металлическим чехлом в бро-

моформ, играющий роль подушки.

Так как основная цель рассматриваемой операции состоит в сепарации

и концентрации акцессорных минералов, разработаны и другие способы,

улучшающие сепарацию, в частности использование ручного и электриче-

ского магнита или недавно сконструированного изодинамического сепара-

тора Франца. Эти способы сепарации могут применяться либо в качестве

собственно метода, либо в сочетании с тяжелыми жидкостями. Различные

приемы сепарации наиболее полно описаны Милнером [301]. Следует под-

черкнуть, что эти приемы в основном нацелены на концентрацию акцессор-

ных минералов п. там, где возможно, на сепарацию каждого минерального

вида в особую фракцию. Для удаления из изучаемой пробы отдельно более

грубых и тонких частиц применяется соответственно просеивание и отмучи-

вание. Эта операция основана на том, что акцессорные минералы по размеру

обычно располагаются между средними песчинками и грубыми илистыми

частицами, эффективно в пределах от 500 до 30 мк (1—5 ф-единиц). Если

задача исследований состоит в оценке относительных количеств различных

минеральных видов путем подсчета во фракциях, остаток разделяют на под-

12-429

178

ГЛАВА 10

классы (на нодфракции), что неизбежно приводит к появлению новых ошибок

опробования (см. следующий раздел), в связи с чем такую методику вряд ли

можно считать целесообразной. Если же основная цель заключается в диаг-

ностике, разделение по минеральным видам является большим достижением

и выделенные фракции можно затем изучать с помощью рентгеноскопиче-

ского либо химического анализа. В этом смысле окончательное решение

определяется в зависимости от цели исследования, а ясно намеченная цель

играет весьма существенную роль при выборе подходящей методики.

После отделения тяжелой фракции ее следует промыть. Кислотами

удаляют железистые пленки, органическими растворителями — остатки

нефти, с помощью других растворителей — различные маскирующие пленки

[300]. Наконец, приготовляют препараты по фракциям, т. е. помещают зерна

в специальные смолы, легко разжижающиеся при нагревании и застывающие

при охлаждении

. Если предполагаются значительные затруднения с диаг-

ностикой, препарат изготовляют с применением какой-либо жидкости

с известным показателем преломления, которую можно легко заменить-

другой. Установка и отбор акцессорных минералов в препарате — важный

шаг, особенно в том случае, если необходим подсчет содержаний минералов.

Если количество имеющихся зерен превысит то, которое можно поместить

в препарат, естественно, возникает вопрос об отборе зерен для препарата.

Существуют различные способы деления, при которых возникающие 'при

делении изменения можно контролировать [229, 316, 449]. При необходи-

мости количественных определений нужно обеспечить гомогенное распре-

деление зерен по площади препарата; Аллен [11] рекомендует изготовлять

специальные шлифы с сеткой

, облегчающей процедуру подготовки препарата.

Тщательная подготовка препарата совершенно необходима и является

залогом правильной диагностики минералов и верной оценки их количест-

венных соотношений.

10.5. ОПРЕДЕЛЕНИЯ КОЛИЧЕСТВЕННЫХ СООТНОШЕНИЙ

АКЦЕССОРНЫХ МИНЕРАЛОВ

По мере усовершенствования методики чисто описательные исследова-

ния, при которых регистрировалось наличие или отсутствие того или иного

минерального вида, сменялись количественными определениями [36, стр. 69].

Сначала это были лишь субъективные определения относительной частоты

встречаемости, но уже в 1898 г. Артини ввел числовую шкалу для оценки

относительных количеств, по которой минералы, составляющие очень малую

часть препарата, оценивались числом 10, а составляющие основную часть —

числом 1. На этом этапе исследований уровень получаемой информации был

либо номинальным (разделение зерен на группы — минеральные виды),

либо порядковым (приближенная оценка частоты встречаемости; см. раз-

дел 12.5). Шкала, предложенная Салмоджарги [382], обеспечивала тот же

уровень информации, что и шкала Артини, но шкала Салмоджарги отме-

чалась обратными значениями оценок: большему количеству минералов соот-

ветствовало большее число. Флит [131] предложил оценивать частоту встре-

чаемости с помощью подсчета числа зерен данного минерала. В 1931 г.

Драйден, рассматривая проблему точности и воспроизводимости результатов

подсчетов, предложил пользоваться «вероятной ошибкой» как оценкой точ-

ности подсчета. Риттенхаус [354] трансформировал кривые Драйдена

с помощью логарифмической шкалы в прямые линии с целью облегчить

процесс оценки точности определений.

Например, канадский бальзам, пиперин или хиракс, показатели преломления

которых равны соответственно 1,54; 1,68 и 1,70.

Такие шлифы поставляет «Катрок Инжиниринг Компани», Лондон.

АКЦЕССОРНЫЕ МИНЕРАЛЫ

179

С введением подсчетов уровень информации вновь повысился, на этот

раз до интервального. Но, ввиду того что нуль в шкале подсчета прирав-

нивается к минералам «неустановленным», эту шкалу нельзя считать совер-

шенной. Так как величина интервала между процентными показателями,

например между 25 и 50%, не фиксирована, то в общем уровень получаемой

информации вряд ли достигает здесь интервального.

Если для оценки соотношений минералов принят метод подсчета, необ-

ходимо стандартизировать методику подсчетов. Препарат с зернами тяжелых

минералов, помещенный на специальном механическом столике, рассмат-

ривается под микроскопом. Подсчеты проводятся либо по линиям, пересе-

кающим препарат, либо по полям зрения. Обычно более предпочтителен

подсчет по линиям, потому что при простом перемещении шлифа зрение

оператора устает значительно меньше; кроме того, по линии каждое зерно

можно помещать в центр поля зрения, что очень важно для диагностики.

В большинстве случаев непрозрачные акцессорные минералы количественно

превышают прозрачные. Так как непрозрачные минералы определяют под

микроскопом при отраженном свете, то перед последующими процедурами

нужно как можно быстрее исключить из анализа непрозрачные минералы.

Голландской школой петрографов

разработана методика, согласно которой

100 зерен пробы сначала классифицируют на прозрачные и непрозрачные,

затем анализируют 100 или более зерен только прозрачных минералов. Эта

методика имеет ряд преимуществ. Например, если анализируемая проба

на 90% состоит из непрозрачных минералов и в ней насчитано 100 прозрач-

ных зерен, эта операция эквивалентна подсчету 1000 зерен первоначальной

пробы. Так как непрозрачные минералы редко используются для различных

интерпретаций, рассмотренную методику можно считать вполне эффективной

для достижения большей точности подсчетов и способствующей уменьшению

трудностей, возникающих при статистическом анализе процентных соот-

ношений минералов [263, 436].

Теперь предположим, что распределение какого-либо вида тяжелых

минералов, например граната, биномиально. Пусть среди N зерен прозрач-

ных минералов в препарате имеется P зерен граната. Тогда по каждому

пересечению шлифа получается оценка X

для Р, и если сосчитано η (п <С N)

зерен, тогда X, среднее по Xi, будет подходящей оценкой P при условии

что пересечения являются случайными выборками тяжелых минералов

в шлифе. Если сосчитаны все N зерен, число кристаллов граната будет рав-

ным Р, т. е. числу зерен, присутствующих в препарате. Практически в пробе

подсчитывается τι зерен. Мы исходим из того, что по мере приближения

η к N значение X стремится к P (см. разделы 2.3 и 12.6). Оценка точности

подсчета обычно представляется как некоторая функция стандартного откло-

нения (в), которое при биномиальном распределении равно σ = у NPQ

(см. раздел 14.2). Тогда оценку количества зерен граната

можно предста-

вить как X ± VX (1 — X). Вероятная ошибка, которую Драйден реко-

мендовал понимать как функцию стандартного отклонения, выражается так:

Можно допустить, что с ростом величины τι подходящей аппроксимацией

для биномиального распределения будет нормальное (см. раздел 14.2) и что

Группа выдающихся минералогов-специалистов по акцессорным минералам; в нее·

входят Дуглас, Кромелин, Андел и многие другие. Группу возглавляет Эдельман (город.

Вагенпнген).

Эту оценку можно выразить в процентах, разделив ее значение на η и умножив

на 100. Например, процент граната равен (NPlN) 100, или оценка составляет (100Х)/п,

а так как X = пр, она равна IOOjo; подобным образом ~γ~Χ (1 — X)

—-

Vpnq, или в про-

центах это составляет ~[/pqln.

Вероятная ошибка (число

(10.1)

12*

180

ГЛАВА 10

среднее значение ±1 стандартное отклонение охватывает около 67,45%

площади, ограниченной кривой нормального распределения, т. е. вероят-

ность попадания данного наблюдения в интервал μ ± σ равна 67,45%

(см. раздел 13.7). Тогда вероятная ошибка представит интервал μ + 0,6745σ,

или 50% площади, ограниченной кривой нормального распределения.

Поэтому для любого данного наблюдения имеются равные шансы попасть

или не попасть в этот интервал. Проще использовать интервал μ + ка,

где к = 2 или 3, который, таким образом, охватывает соответственно 95,4

и 99,7% площади, ограниченной кривой. Если следовать обычным рекомен-

дациям, основанным на биномиальном распределении, «ошибку подсчета»

2 !/

Z (1 — X) можно оценить довольно легко, рассчитав значение X.

В табл. 10.3 приведены величины этой ошибки для наиболее представитель-

ной серии значений X. Легко заметить, что ошибки распределены симмет-

рично относительно максимума кривой. Далее, вероятность попадания новой

Таблица 10.3

Оценка «ошибок подсчета»

Среднее

1-Х

npq Vnpq

2 Ynpq

Среднее

1-Х

npq

,у τ (.-I)

5 0,05

0,95

4,75

2,18

4,36

0,90

0,90 . 9,00

3,00

6,00

0,20 0,80 . 16,00

4,00

8,00

0,30 0,70

21,00

4,58 9,16

0,40 0,60 24,00 4,90 9,80

0,50 0,50

25,00

5,00 10,00

0,60 0,40 24,00 4,90

9,80

0,70

0,30 21,00

4,58 9,16

0,80

0,20 16,00 4,00 8,00

0,90

0,10

9.00 3,00 6,00

95 0,95

0,05 4,75 2,18 4,36

оценки в интервал 50 + 10 находится на 95%-ном уровне, так что для 100

подсчитываемых зерен ожидаемый интервал составляет от 40 до 60 зерен.

При таких условиях более надежный подход заключается в использо-

вании каких-то частей пробы и интервала X + ках, где к = 2 или 3 и σ·^ =

= σ[γ~η. Путем правильного подбора величины η ошибку определения сред-

них для частей пробы можно контролировать (см. раздел 2.6). Например,

предположим, что имеется четыре серии, в каждой из которых находится

по 25 зерен, т. е. P — 50. Тогда интервал X + 2 Οχ = 50 ± 2α[γ~η, или

2 -

50 ± g σ. Таким образом, целесообразно проводить подсчеты в небольших

сериях.

При биномиальном распределении по случайным выборкам получаются

несмещенные состоятельные оценки (см. раздел 12.6). Но допущение о слу-

чайном характере опробования биномиальной совокупности эквивалентно

принятию модели постоянной вероятности, а это в свою очередь требует

определенных характеристик опробуемой совокупности (см. раздел 14.3).

Физически это означает, что гранат по подсчетам в разных пересечениях

имеет постоянную встречаемость, поэтому чрезвычайно важно, чтобы пре-

парат был равномерным. Лишь в этом случае принятие модели постоянной

вероятности будет оправданным (см. раздел 14.3). Ниже будет показано,

АКЦЕССОРНЫЕ МИНЕРАЛЫ 181

что практически чрезвычайно трудно приготовить препарат, удовлетворяю-

щий этим требованиям. Чтобы достигнуть лучшего контроля в процессе

подсчета и приготовления препарата, Аллен [11] предложил использовать

стекла с размеченной на них сеткой. Без контроля равномерности подсчеты

могут привести к смещенным оценкам и полученные значения соотношений

минералов не будут представлять истинных соотношений минеральных

видов в препарате.

Значительное колебание количественных соотношений тяжелых мине-

ралов в разных пробах одного и того же слоя — обычное явление. В силу

этого Эванс, Хейман и Мейджид [117] предложили пересчитывать процент-

ные соотношения, получаемые при подсчетах, и выражать их в новой шкале,

сглаживая, таким образом, случайные помехи. На этой новой шкале нулевая

точка не имеет физического смысла и цена делений шкалы разная. Такую

шкалу надо считать шагом назад, так как с ее помощью нельзя получить

порядковый уровень информации, следовательно, подсчет становится беспо-

лезной операцией, а «ошибка в подсчете»— бессмысленной

Крамбейн и Расмуссен [253] пытались дифференцировать и сравнить

источники изменчивости в оценке соотношений тяжелых минералов. Они

обнаружили, что общая лабораторная ошибка приблизительно равна поле-

вой ошибке, возникающей при опробовании, и что «ошибки» в весовых про-

центах тяжелых минералов больше, чем ошибки в частостях встречаемости.

Для достижения более полного контроля в процессе фракционирования

тяжелых минералов эти исследователи рекомендовали пользоваться центри-

фугой (см., кроме того, [356]). Они нашли также, что ошибки в разделении

исходной пробы при отборе препарата для изучения, а также ошибки в при-

готовлении препарата и в подсчете зерен примерно в три раза больше, чем

ошибки, получаемые от разделения исходной пробы путем просеивания

и сепарацией в бромоформе. Таким образом, основные ошибки, по их мнению,

возникают на заключительной стадии лабораторного изучения.

Приведенный обзор убеждает в том, что лишь весьма существенные

изменения в количественных соотношениях минералов, выдерживающиеся

по всему региону, могут быть использованы для геологической интерпрета-

ции. И если колебания в соотношениях действительно представляют реаль-

ный интерес, отбор объектов наблюдения должен строго контролироваться.

Осуществлять контроль наиболее целесообразно с помощью препаратов,

приготовленных простейшим способом. Так как после дезинтеграции влияние

способа отбора пробы на колебание в распределении минеральных видов

можно считать аналогичным трансформации распределения Пуассона в бино-

миальное распределение (см. раздел 14.7), то для избежания дальнейших

осложнений желательно изучать всю дезинтегрированную пробу без сокра-

щений. В этом случае для проверки адекватности приготовленного препарата

подходящей моделью будет распределение Пуассона [171]. Так можно избе-

жать многих ошибок, возникающих в результате разделения исходной

пробы.

Если полученная путем подсчета оценка действительно представительнее

для распределения минеральных видов в анализируемой пробе, можно изу-

чить изменчивость между пробами. Чтобы установить, действительно ли

репрезентативна эта изменчивость минералов для какого-то геологического

тела, необходимо узнать распределение минеральных видов в «натуре»

(«реальном мире»). Некоторые возможные распределения рассматриваются

в разделах 14.5 π 14.10 и в работе [171]. К настоящему времени наиболее

реальной моделью из «реального мира» представляется отрицательная бино-

миальная модель (см. также [11]).

В данном случае правильность арифметической процедуры для определения сред-

него значения и стандартного отклонения сомнительна.