Гриффитс Дж. Научные методы исследования осадочных пород
Подождите немного. Документ загружается.


162
ГЛАВА 10
9.3.4. Элементы класса А В, внешне (Л ) и внутренне (В) прерывистые
Карбонатный цемент чаще всего встречается в виде небольших участков,
заполняющих поры в осадочных породах (фиг. 9.7). В этом случае он внут-
ренне прерывистый (А — поликристалличность) и внешне прерывистый
(В — неправильные контуры). Если карбонатный цемент составляет свыше
30% от площади шлифа, то такая разновидность называется «песчаным
известняком».
Другим элементом, который может быть классифицирован как внут
ренне и внешне прерывистый (AB)
1
является материал, называемый матри-
цей, или заполняющим веществом [270, стр. 138]. Pasviep зерен этого слож-
ного по составу материала изменчив, но обычно этот последний более тонко-
зернистый, чем элементы класса AB. Трудно дать точные критерии для его
Фиг. 9.7. Микрофотография шлифа
миссисипских субграувакковых песча-
ников формации Поконо (Алтуна, Пен-
сильвания) .
Видны зерна кварца и кварцитов. Типичный
для слюдистой матрицы облик. Николи скре-
щены; X 150. Каталог Пенсильванского уни-
верситета (из коллекции X. В. Шейдла).
Фиг. 9.8. Микрофотография пенсиль-
ванского песчаника формации Фаунтин
(Ред-Кросс-Парк, Колорадо).
Видны зерна полевого шпата и кварца; хоро-
шо выражена морфология кристаллического
карбонатного цемента. Николи скрещены;
X 100. Каталог Пенсильванского универси-
тета № 8506 (из коллекции Дж. Х-уберта).
идентификации из-за сложности состава, включающего по крайней мере
глинистые минералы, материал цемента (кремнистого или карбонатного),
недоступный для диагностики, мельчайшие частицы кварца и другие мине-
ралы (фиг. 9.8); данное Браммаллом [38] определение сетки иллюстрирует
потенциальную сложность характера матрицы.
Этот материал типичен для таких пород, как граувакки (субграувакки
и граувакки) и аркозы, но в общем он встречается редко, а в кварцитах его
совсем не бывает. Очень часто матрицей называют тот самый материал,
который оптически определяется в шлифах лишь с большим трудом. В силу
этих особенностей формы нахождения и распределения в шлифах, вероятно,
являются наилучшими критериями для диагностики матрицы.
Матрица отличается от обломков глин класса AB по морфологии. Сле-
дует помнить, что по морфологическим признакам обломки местного про-
исхождения не всегда отличаются от принесенных издалека; другими сло-
вами, необходимы дополнительные критерии, чтобы можно было отличать
обломки ранее существовавших глин предположительно обломочного про-
исхождения от обломков матрицы, характеризующихся непрерывным внеш-
ним габитусом, обусловленным некоторыми наложенными процессами,
нарушившими первичное сложение породы [174, фиг. 2].
В большинстве случаев остальные элементы, лежащие за пределами
этих подклассов, можно объединить под рубрикой класса «другие». Эти
элементы, вместе взятые, следует определять с помощью доступных мор-

КОЛИЧЕСТВЕННО-МИНЕРАЛОГИЧЕСКИЙ АНАЛИЗ
163
фологических критериев и впоследствии более точно дифференцировать
путем детальных исследований.
При подсчете точек целесообразно пользоваться небольшим количе-
ством подклассов. Эта рекомендация особенно справедливой бывает в том
случае, когда оператор не уверен, к какому подклассу следует отнести
какой-нибудь элемент; чем больше выбор, тем утомительнее процедура
подсчета и тем менее близкими оказываются результаты. Восьми подклассов
вполне достаточно для любого частного подсчета. Если же есть необходи
мость в большей детальности, нужно произвести новый подсчет, обратив
при этом особое внимание на подразделения внутри подклассов. Такой
двойной подсчет дает более достоверные оценки но сравнению с попыткой
выделить те же подразделения при первом подсчете. Чтобы дать основную
оценку типов и соотношений обычно встречающихся элементов, для пред-
варительных исследований фактически достаточно четырех главных классов.
9.4. ИСПЫТАНИЕ МЕТОДИКИ IIA СХОДИМОСТЬ РЕЗУЛЬТАТОВ
После того как выбрана серия классов для анализа методом подсчета
точек, следует начать анализ с предварительного эксперимента, имеющего
основную цель — испытать сходимость классификации. Оператор должен
произвести повторные подсчеты в различные дни, чтобы решить, приобрел
ли он достаточно устойчивые навыки для работы.
Если в получении результатов предварительного эксперимента прини
мали участие несколько операторов, следует провести более совершенный
эксперимент с участием этих операторов.
В настоящее время уже не надо доказывать, что для химического ана-
лиза требуются определенные стандарты и унифицированная методика;
при таком анализе получить дублированные результаты легче, чем проце-
дурой, подобной подсчету точек, которая зависит от искусства оператора
и от состояния оператора (например, от степени его усталости). Проверка
на сходимость результатов подсчета в тонких шлифах гранитов описана
Чейсом и Фэрбэрном [59], а осадочных пород — Гриффитсом и Розенфельдом
[161]. Некоторые рекомендации для таких испытаний даются в настоящей
книге.
Прежде всего мы должны проверить сходимость некоторых определений
подклассов по η разным шлифам и ρ операторам. Анализ шлифов будет
проведен с помощью t пересечений в каждом шлифе, и места этих t пересе-
чений должны быть взяты наугад каждым оператором. Чтобы добиться
приближения к модели бесконечной совокупности (см. гл. 18 и ниже), необ-
ходимо провести многократные замеры по каждому шлифу. Схема таких
операций дана в табл. 9.2.
Таблица 9.2
Схема эксперимента для проверки гипотезы отсутствия
воздействия операторов и шлифов
Источник изменчивости
Число степеней
Свободы
Ожидаемый средний квадрат
Между операторами
Между шлифами
Операторы χ шлифы
Линии (по операторам
шлифам)
Сумма дисперсий
(р-1) (W-I)
и тр (t — 1)
P-1
т.
— 1
Ί+^VB
ftno
P
п
2 4- ta
2
+tpa^
т
mpt —
1
^tot
11*

164
ГЛАВА 10
Сходимость проверяется путем сравнения ожидаемых средних квадратов
(чистый компонент изменчивости), полученных операторами по шлифам
со значениями по пересечениям в виде отношения дисперсий F:
2 . 2
σ
3
СТтр
; степени свободы
—
(ρ— 1) (т
—
1) и mp(t— 1).
σ
ε
Увеличивая число пересечений, можно повышать чувствительность
критерия до требуемого уровня. Далее, дисперсии по линиям пересечения
можно изучить, группируя значения по линиям в небольшие серии, напри-
мер в каждом из пяти пересечений выделяется по 30 серий, в каждой серии
объединяется пять точек. Необходимо отдавать себе отчет в том, что, если
расхождения между дисперсиями несущественны, причиной этому служит
либо близость соответствующих или средних значений, либо большая несхо-
димость определений, произведенных операторами в разных шлифах.
Сходимость результатов, полученных разными операторами, можно
проверить сравнением их подсчетов по одному и тому же пересечению. Чтобы
установить сходимость данных по подклассам, необходимо использовать
очень гибкую схему проверки с довольно большим числом изучаемых ком-
понентов. Большую помощь в этом отношении оказывают графики анализов
дисперсии, по которым можно судить о качестве анализа (см. [161, фиг.
на стр. 80], а также раздел 15.6, фиг. 15.5 настоящей книги).
Весьма рекомендуем иметь небольшую серию шлифов в качестве стан-
дартов; операторы, начинающие данный анализ, должны их анализировать.
Тем самым еще до начала анализа можно добиться точных наблюдений опе-
раторов. Если намечаются значительные по масштабам аналитические работы
рассматриваемого типа, коллекция стандартных шлифов, в которой разные
типы пород представлены несколькими шлифами, окажется особенно необ-
ходимой.
9.5. ПРОЦЕДУРА И МЕТОДИКА
Процедура точечных подсчетов довольно проста. Необходимая аппара-
тура состоит из столика для точечных подсчетов и счетчика. Существует
несколько конструкций как столиков, так и счетчиков.
Столиками можно манипулировать вручную либо контролировать их
автоматически. Стандартный столик, сконструированный для ручного под-
счета точек в тонких шлифах, продается в «Америкэн Оптикал Компани».
Стандартный автоматический столик легко усовершенствовать. Вполне
подходящей является модель столика Бауха и Лома, усовершенствованная
Розенфельдом [366].
Для регистрации подсчетов пользуются также счетчиками кровяных
телец. Наиболее удобны счетчики, которые регистрируют данные по восьми
классам и общее значение. Другой тип — деноминаторные счетчики — так-
же имеют разные размеры и вполне доступны. Такие счетчики можно уста-
новить на четыре, шесть или восемь каналов записи. Автоматический элек-
трический счетчик, который можно приобрести у «Свифт энд Сан Лимитед»,
состоит из столика для подсчета точек, соединенного со счетным устройством.
Показания счетчиков лучше всего заносить в специальный журнал;
одна из возможных форм журнала, пригодная для обычных исследований,
приведена в табл. 9.3.
Для ускоренного подсчета и уменьшения ошибок диагностики можно
пользоваться увеличенным изображением. В большинстве случаев для оса-
дочных пород удобно увеличение в 100—250 раз. Расстояние между линиями
замеров, естественно, не зависит от степени увеличения. При анализе оса-
дочных пород целесообразно проводить подсчеты по сближенным линиям.
Обычно на счетных столиках пользуются следующими расстояниями: 0,5 мм

КОЛИЧЕСТВЕННО-МИНЕРАЛОГИЧЕСКИЙ АНАЛИЗ 151
Таблица 9.3
Таблица точечного подсчета минерального состава
Шлиф Микроскоп Тип
Порода Столик
Объектив Окуляр
Начальное положение —, по ν по H № пересечения -
Положение шлифа Длина линии
Оператор Расстояние между линиями
Примечания:
№ клавиша 123456789 10 Табулятор
Минерал
2
3
4
7
8
9
10
Сумма
Среднее значение
между вертикальными линиями и 0,3 мм между горизонтальными. В неко-
торых случаях эти расстояния уменьшают, пользуясь квадратной сеткой
окуляра, которая является далеко не лишним дополнительным атрибутом
при детальных исследованиях.
Перед началом эксперимента нужно просмотреть шлиф и убедиться
в том, что площадь его достаточна для подсчетов и что шлиф правильно
изготовлен. Обычно считается, что точки должны располагаться по линиям
прямоугольной сетки. Однако это требование несущественно. Линии могут
отклоняться от одного направления. Иногда пересечения в разных направ-
лениях оказываются даже необходимыми (см., например, работу [226]).
После предварительного просмотра шлифа можно приступить к выбору
системы классов и подклассов, которая нужна для данного исследования.
Однако до окончательного выбора следует выполнить несколько пробных
подсчетов с тем, чтобы удостовериться в стабильности диагностики опера-
тора, так как лишь в этом случае будет получена достаточно точная оценка
состава. Если оператор достаточно опытен, предварительные испытания

166
ГЛАВА 10
можно значительно упростить. Подсчеты, полученные при предварительных
испытаниях, в анализе не учитываются.
Результаты точечного подсчета выражают числом элементов в классах
и подклассах. Для стабильных оценок средних значений по шлифам Чейс
[631 рекомендовал производить определения в количестве 1000 точек на шлиф.
Вероятно, что для некоторых осадочных пород нужно еще большее число
подсчетов. В качестве первого шага анализа желательно получить оценку
принятой схемы опробования, т. е. расположения проб. Для этой цели
из всей серии шлифов, подлежащих анализу, выбирают несколько шлифов
(например, четыре), отражающих самые разнообразные породы. В этих
шлифах проводят замеры на 10 линиях по 100 точек в каждой. Если это
необходимо, точки группируют в небольшие серии. После этого стабиль-
ность полученных оценок можно проверить по индексу дисперсии (см. гл. 14
и работы [127, 171, 174, 416]). Если выявляется стабильность оценки, анализ
можно продолжать. Но если оценка нестабильна, например χ
2
превышает
практическое значение при уровне P <С 0,05, линии подсчетов следует как-то
объединить. Цель этой процедуры состоит в необходимости убедиться, что
окончательная программа опробования может обеспечить получение слу-
чайных проб анализируемой генеральной совокупности. После этого задают-
ся наиболее вероятным характером распределения значений, получаемых
в результате анализа шлифов осадочных пород. Этот вопрос рассматривали
Чейс [55] применительно к гранитам и Гриффите [171, 174] — к осадочным
породам.
Для подклассов, составляющих от 5 до 95% шлифа, вполне подходящей
моделью можно считать биномиальное распределение, в то время как для
подклассов, слагающих меньше 5% и больше 95%, соответствующей моделью
будет распределение Пуассона. В обоих этих случаях требуется строгое
выполнение условий опробования (см. гл. 14 и работу [171]).
Очень часто компоненты породы в шлифе такие, что условия опробова-
ния выполнить не представляется возможным; в таком случае пользуются
альтернативными моделями — гипергеометрической [55] и отрицательной
биномиальной [171, 172]. Для слоистых пород можно ожидать распределе-
ний Лексиана и Пуассона (см. раздел 14.6 и работы [233, 444]).
Несколько примеров манипуляций, необходимых для сравнения наблю-
даемой частоты встречаемости с ожидаемой, описывается в гл. 14 настоящей
книги, а также в других работах автора [171, 172].
В окончательном виде данные анализа будут выражены в виде средних
вначений и стандартных отклонений, а частота встречаемости может иллю-
стрироваться гистограммами. Некоторые примеры приведены в разделе 9.6,
а также в гл. 14.
9.6. ПРИМЕРЫ ИЗУЧЕНИЯ КОЛИЧЕСТВЕННО-МИНЕРАЛЬНОГО
СОСТАВА ОСАДОЧНЫХ ПОРОД
Чтобы проиллюстрировать характер ожидаемых результатов точечного
подсчета элементов в шлифах, можно рассмотреть в качестве примеров
некоторые известные в литературе эксперименты.
В процессе одного такого эксперимента пять операторов выполняли
анализ трех шлифов из одного и того же образца кварцитов формации Ори-
сканп. В каждом из шлифов замерялось по 15 линий со 102 точками на линии.
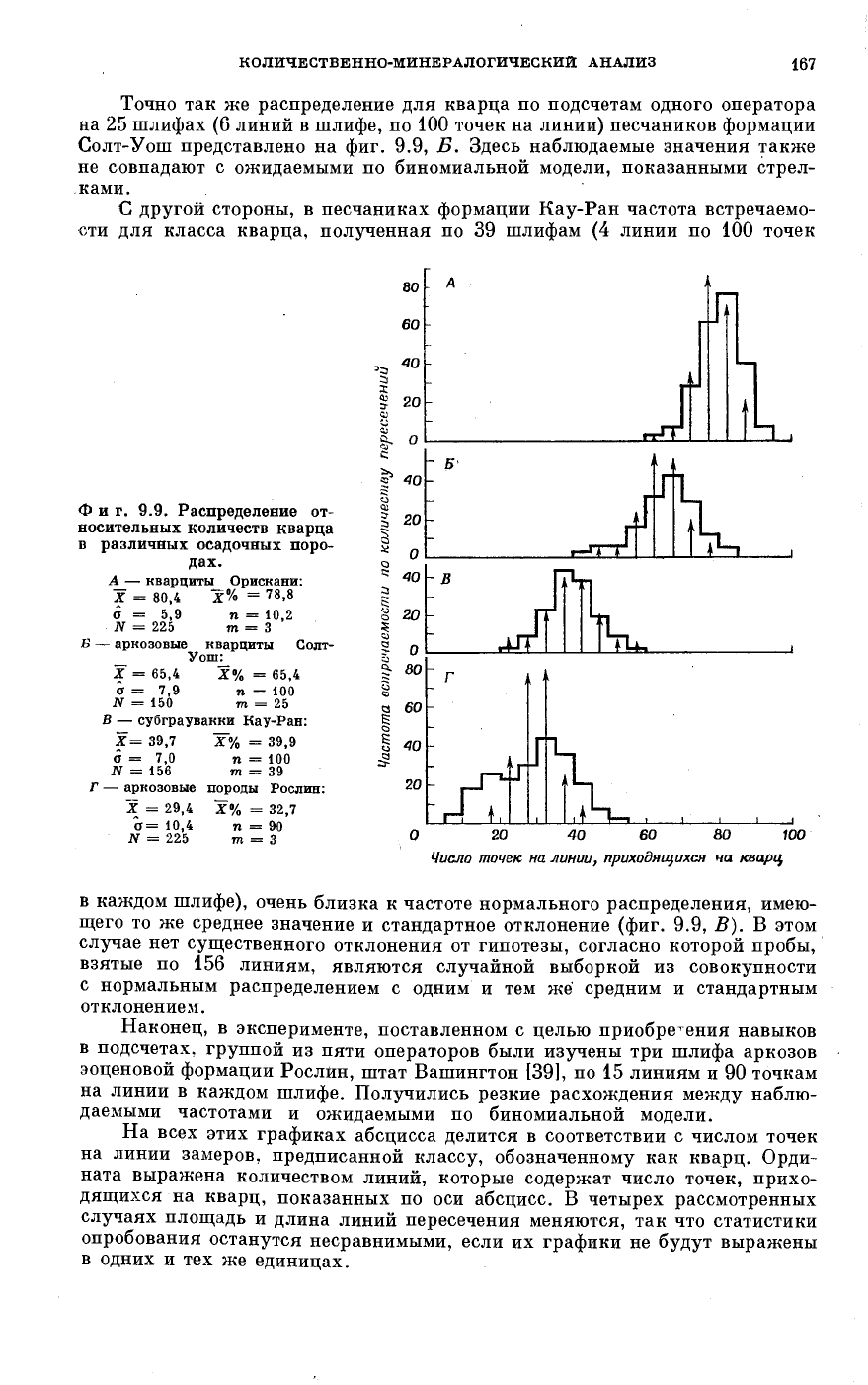
Частота встречаемости для кварца показана на фиг. 9.9. Ожидаемое распре-
деление для тех же средних значений выражено в виде стрелок. Расхож-
дения здесь очевидны, и, по-видимому, они служат указанием либо на неслу-
чайный характер опробования (расположения линий), либо на непримени-
мость биномиальной модели.
КОЛИЧЕСТВЕННО-МИНЕРАЛОГИЧЕСКИЙ АНАЛИЗ
151
Точно так же распределение для кварца по подсчетам одного оператора
на 25 шлифах (6 линий в шлифе, по 100 точек на линии) песчаников формации
Солт-Уош представлено на фиг. 9.9, Б. Здесь наблюдаемые значения также
не совпадают с ожидаемыми по биномиальной модели, показанными стрел-
ками.
С другой стороны, в песчаниках формации Кау-Ран частота встречаемо-
сти для класса кварца, полученная по 39 шлифам (4 линии по 100 точек
80
60
.Jtl
40
20
JL
ZL
- 5
40
Φ и г. 9.9. Распределение от-
носительных количеств кварца
в различных осадочных поро-
дах.
А — кварциты Орискани:
X = 80,4 Х% = 78,8
σ = 5,9 η = 10,2
N = 225 т = 3
В — аркозовые кварциты Солт-
_ Уош:
X = 65,4
20
40
20
- В
Х% = 65,4
η = 100
m = 25
В — субграувакки Кау-Ран:
S- 80
а = 7,9
N = 150
X= 39,7
<7
= 7,0
N = 156
= 39,9
η = 100
m = 39
Г — аркозовые породы Рослин:
X = 29,4 Х% = 32,7
60
40
ZO
O= 10,4
N = 225
η = 90
m = 3
О 20 40 60 вО 100
Число точек на линии, приходящихся на кварц
в каждом шлифе), очень близка к частоте нормального распределения, имею-
щего то же среднее значение и стандартное отклонение (фиг. 9.9, В). В этом
случае нет существенного отклонения от гипотезы, согласно которой пробы,
взятые по 156 линиям, являются случайной выборкой из совокупности
с нормальным распределением с одним и тем же средним и стандартным
отклонением.
Наконец, в эксперименте, поставленном с целью приобре
т
ения навыков
в подсчетах, группой из пяти операторов были изучены три шлифа аркозов
эоценовой формации Рослин, штат Вашингтон [39], по 15 линиям и 90 точкам
на линии в каждом шлифе. Получились резкие расхождения между наблю-
даемыми частотами и ожидаемыми по биномиальной модели.
На всех этих графиках абсцисса делится в соответствии с числом точек
на линии замеров, предписанной классу, обозначенному как кварц. Орди-
ната выражена количеством линий, которые содержат число точек, прихо-
дящихся на кварц, показанных по оси абсцисс. В четырех рассмотренных
случаях площадь и длина линий пересечения меняются, так что статистики
опробования останутся несравнимыми, если их графики не будут выражены
в одних и тех же единицах.
168
ГЛАВА 10
Среднее Значение X равно пр, где η — число точек на линии. Чтобы
сравнить ^средние значения, каждое из них выражается в процентах путем
деления X на η и умножением на 100.
Стандартные отклонения также не сопоставимы без соответствующих
пересчетов в одни и те же единицы. Ряд других примеров можно найти
в гл. 14 и в цитированной литературе.
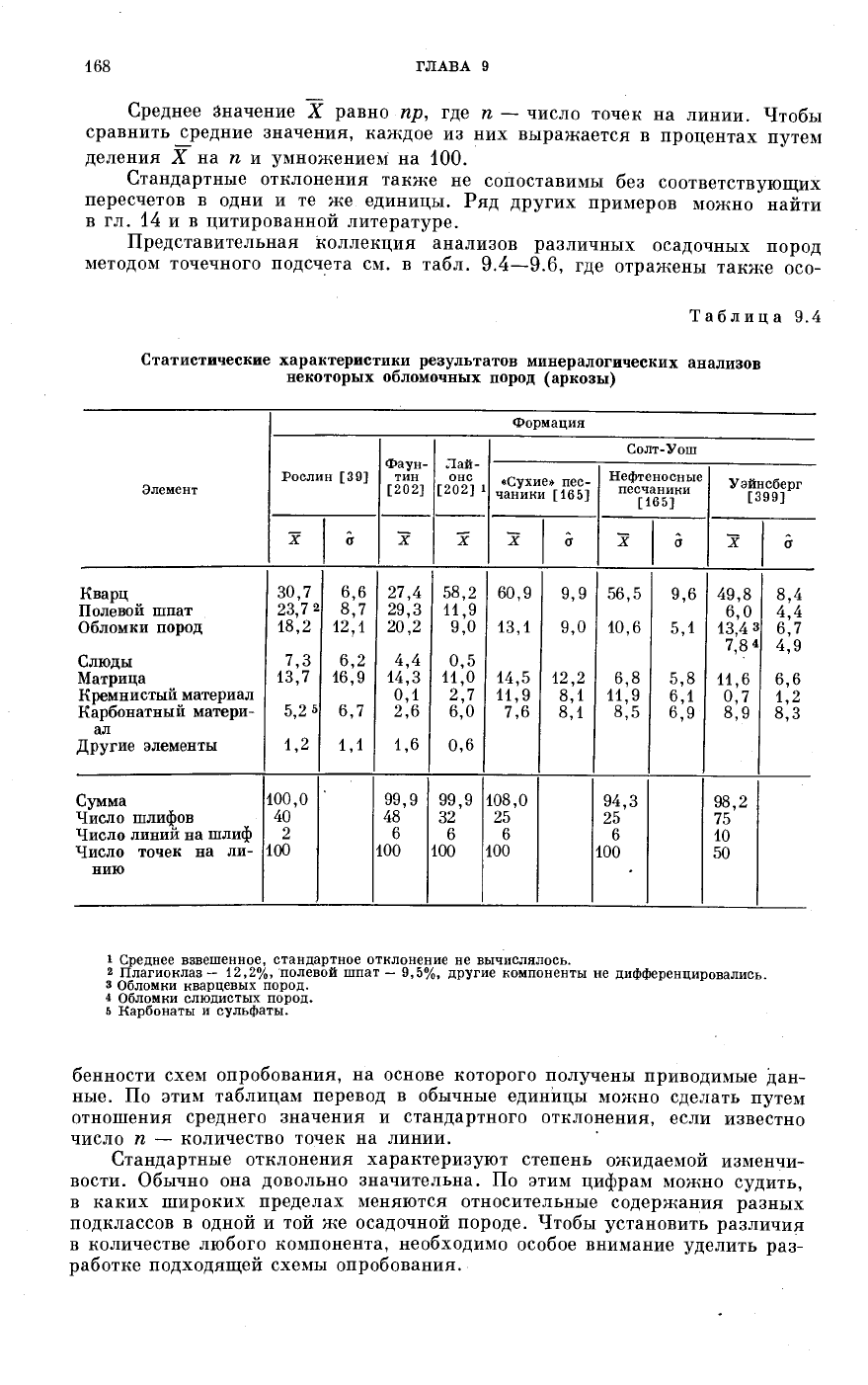
Представительная коллекция анализов различных осадочных пород
методом точечного подсчета см. в табл. 9.4—9.6, где отражены также осо-
Таблица 9.4
Статистические характеристики результатов минералогических анализов
некоторых обломочных пород (аркозы)
Формация
Фаун-
тин
[202]
Лай-
OHC
[202] ι
Солт-Уош
Элемент
Рослин [39]
Фаун-
тин
[202]
Лай-
OHC
[202] ι
«Сухие» пес-
чаники [165]
Нефтеносные
песчаники
[165]
Уэйнсберг
[399]
X
σ
X
X
X σ
X
а X
σ
Кварц
30,7 6,6
27,4
58,2
60,9 9,9
56,5
9,6 49,8 8,4
Полевой шпат
23,7
2
8,7
29,3 11,9
6,0
4,4
Обломки пород
18,2 12,1
20,2
9,0
13,1
9,0
10,6
5,1
13,4 3
6,7
7,8^
4,9
Слюды
7,3 6,2 4,4 0,5
Матрица
13,7
16,9
14,3
11,0
14,5
12,2 6,8
5,8
11,6
6,6
Кремнистый материал
0,1
2,7 11,9
8,1
11,9
6,1
0,7
1,2
Карбонатный матери-
ал
Другие элементы
5,2 5
6,7 2,6
6,0
7,6
8,1
8,5
6,9
8,9
8,3
Карбонатный матери-
ал
Другие элементы
1,2
1,1
1,6
0,6
Сумма
Число шлифов
Число линий на шлиф
Число точек на ли-
нию
100,0
99,9
99,9
108,0
94,3
98,2
40 48
32 25
25
75
2 6
6 6 6
10
100
100 100
100
100
50
1
Среднее взвешенное, стандартное отклонение не вычислялось.
2 Плагиоклаз
—
12,2%, полевой шпат
—
9,5%, другие компоненты не дифференцировались.
3 Обломки кварцевых пород.
4 Обломки слюдистых пород.
5 Карбонаты и сульфаты.
бенности схем опробования, на основе которого получены приводимые дан-
ные. По этим таблицам перевод в обычные единицы можно сделать путем
отношения среднего значения и стандартного отклонения, если известно
число η —- количество точек на линии.
Стандартные отклонения характеризуют степень ожидаемой изменчи-
вости. Обычно она довольно значительна. По этим цифрам можно судить,
в каких широких пределах меняются относительные содержания разных
подклассов в одной и той же осадочной породе. Чтобы установить различия
в количестве любого компонента, необходимо особое внимание уделить раз-
работке подходящей схемы опробования.
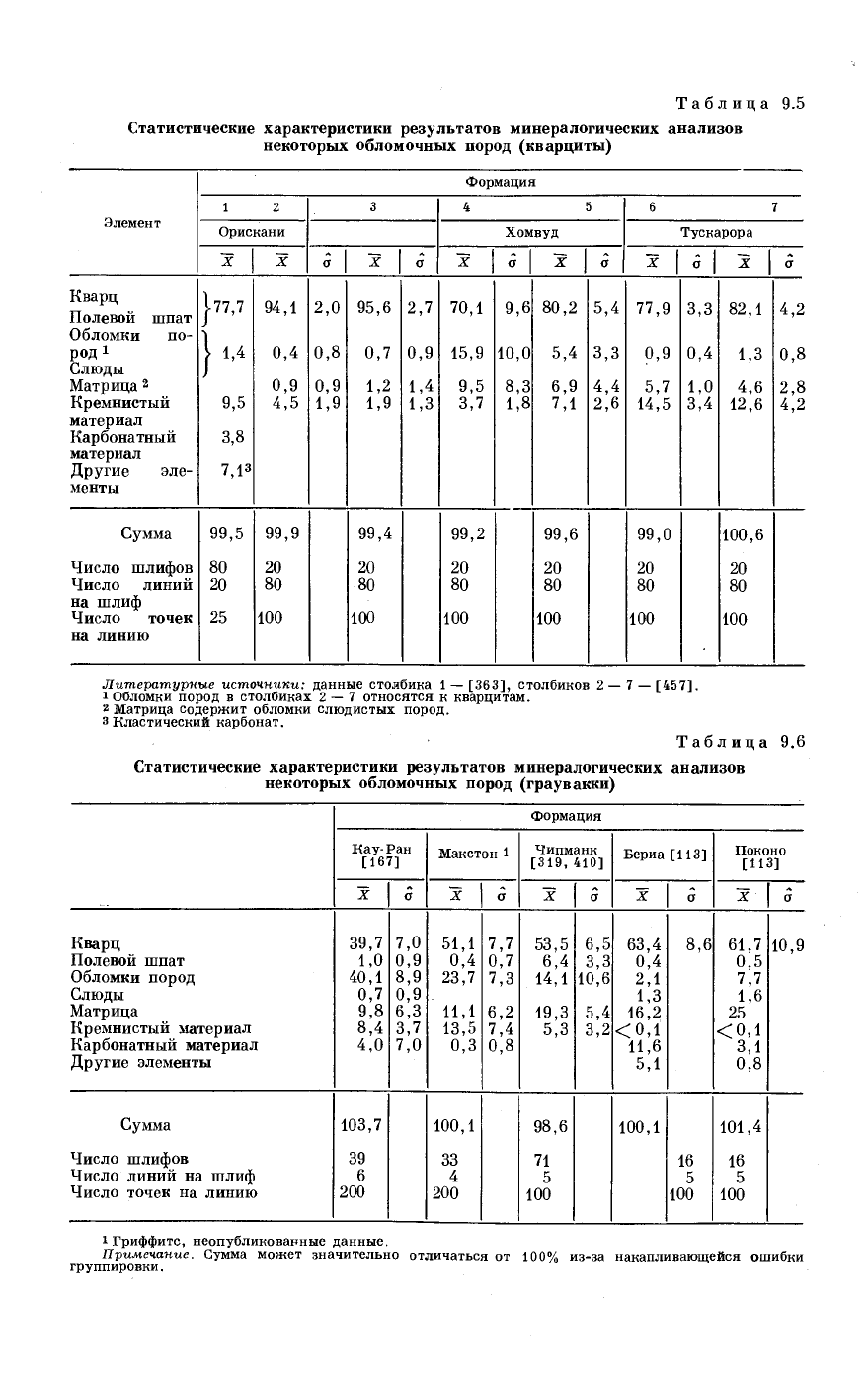
Таблица 9.5
Статистические характеристики результатов минералогических анализов
некоторых обломочных пород (кварциты)
Формация
Элемент
1 2
3
4 6
Элемент
Орискани
Хомвуд
Тускарора
X X
σ X
σ
X
σ
χ
σ X
σ
χ а
Кварц
Полевой шпат
Обломки по-
род
1
Слюды
Матрица
2
Кремнистый
материал
Карбонатный
материал
Другие эле-
менты
^J- 77,7
I IA
9,5
3,8
7,13
94,1
0,4
0,9
4,5
2,0
0,8
0,9
1,9
95,6
0,7
1,2
1,9
2,7
0,9
1,4
1,3
70,1
15,9
9,5
3,7
9,6
10,0
8,3
1,8
80,2
5,4
6,9
7,1
5,4
3.3
4.4
2,6
77,9
0,9
5,7
14,5
3.3
0,4
1,0
3.4
82,1
1,3
4,6
12,6
4,2
0,8
2,8
4,2
Сумма 99,5
99,9 99,4
99,2 99,6
99,0
100,6
Число шлифов
Число линий
на шлиф
Число точек
на линию
80
20
25
20
80
100
20
80
100
20
80
100
20
80
100
20
80
100
20
80
100
Литературные источники: данные столбика 1 — [363], столбиков 2 — 7 — [457].
ι Обломки пород в столбиках 2 — 7 относятся к кварцитам.
2 Матрица содержит обломки слюдистых пород.
3 Кластический карбонат.
Таблица 9.6
Статистические характеристики результатов минералогических анализов
некоторых обломочных пород (граувакки)
Формация
Kay- Ран
[167]
Макстон 1
Чипманк
[319, 410]
Бериа [113]
Поконо
[ИЗ]
X
σ
X
σ
X
σ
X
σ X
σ
Кварц
Полевой шпат
Обломки пород
Слюды
Матрица
Кремнистый материал
Карбонатный материал
Другие элементы
39,7
1,0
40,1
0,7
9,8
8,4
4,0
7,0
0,9
8,9
0,9
6,3
3,7
7,0
51,1
0,4
23,7
11,1
13,5
0,3
7,7
0,7
7.3
6,2
7.4
0,8
53,5
6,4
14,1
19,3
5,3
6,5
3.3
10,6
5.4
3,2
63,4
0,4
2,1
1,3
16,2
<0,1
11,6
5,1
8,6 61,7
0,5
7,7
1,6
25
<0,1
3,1
0,8
10,9
Сумма 103,7
100,1
98,6
100,1
101,4
Число шлифов
Число линий на шлиф
Число точек на линию
39
6
200
33
4
200
71
5
100
16
5
100
16
5
100
!Гриффите, неопубликованные данные.
Примечание. Сумма может значительно отличаться от 100% из-за накапливающейся ошибки
группировки.

ГЛАВА 10
Изучение минералогического состава.
Акцессорные минералы
Минеральные фации какой-либо древней осадочной породы и совре-
менных отложений одного и того же морского бассейна могут быть чрез-
вычайно сходными. В то же время они могут отличаться от других
пород, лежащих непосредственно ниже и выше. Таким образом, каждая
фация будет обладать своей собственной характеристикой.
J. T h о u
1
е t, р. 9, 1913
10.1. ВВЕДЕНИЕ. КОНЦЕПЦИЯ
Исследования акцессорных минералов представляют собой специфиче-
скую область изучения вещественного состава горных пород. Если химиче-
ский состав пород или содержание основных химических компонентов можно
сравнить с минералогическими анализами, то определение акцессорного
состава аналогично определению элементов-примесей. В соответствии с этим
методика исследования акцессорного состава, подобно методике определения
элементов-примесей, требует специальной подготовки и обработки проб для
выделения «элементов». Как в химических, так и минералогических иссле-
дованиях методика сводится к подсчету относительных количеств элементов.
Акцессорными называются минералы, встречающиеся в породах отно-
сительно редко. Они составляют менее
1
% объема изверженных, осадочных
и метаморфических пород. Иногда эти редкие компоненты концентрируются,
например в пегматитах, в основных породах, образовавшихся при ликвации
магмы, в аллювиальных россыпях и в различных рудных месторождениях.
Таким образом, акцессорные минералы часто представляют значительный
практический интерес. Процентные соотношения между наиболее распро-
страненными акцессорными минералами изверженных различных пород
показаны в табл. 10.1. Метаморфические породы, не выделенные в таблице,
в данном случае можно отнести как к преобразованным изверженным, так
и осадочным породам.
Из 3000 минералов, насчитывающихся в земной коре, около 300 доволь-
но часто присутствуют в качестве акцессорных в осадочных породах. В боль-
шинстве случаев в осадочных породах содержится от 10 до 15 минеральных
видов акцессориев·. Но некоторые породы, например черные пески или вул-
канические пески, почти мономинеральны, в то время как другие, например
гляциальные отложения, содержат свыше 50 различных минералов. Гене-
тически акцессорные минералы можно подразделить на аллогенные, или
детритусовые, и аутигенные, или минералы осадочной породы, образовав-
шиеся in situ. Изучение акцессорных минералов используется для диффе-
ренциации областей сноса (поиски источников сноса), выяснения условий
осадконакопления (характеристика окружающей среды) и оценки диагене-

АКЦЕССОРНЫЕ МИНЕРАЛЫ 171
Таблица 10.1
Взаимоотношения между акцессорными минералами изверженных
и осадочных пород
Извер-
Осадоч-
женные
Минералы
ные по-
породы,%
Минералы
роды, %
Породообразующие |
0-65
0—50
0—30
Ортоклаз
Плагиоклаз
Кварц
Амфибол Ί
0-60
0-30
0—95
1 Породообра-
[ зующие
Встречающиеся в пе- f 0—50 \
Пироксен J
<1
Акцессорные
ременных количе- <
0—20
Слюда
0-5
Встречающиеся
ствах I
0—20
J
Оливин
Циркон
Турмалин
1
в переменных
количествах
Акцессорные
<1 <
Апатит
I
<1
I
Акцессорные
1
Гранат
Сфен и т. д.
I
<1
I
Акцессорные
Вторичные
Хлорит
Эпидот
I
)
тических изменений в осадочных породах (изучение парагенезиса пород).
Степень успеха в выполнении этих разнообразных задач, как и следует
ожидать, бывает различной. Некоторые исследователи считают, что изучение
акцессорных минералов обеспечивает получение любой информации, в то
время как другие глубоко в этом сомневаются. В общем в осадочных поро-
дах, залегающих близ дневной поверхности, особенно в кайнозойских отло-
жениях, изучение акцессорных минералов, оказывается, имеет большой
смысл. В случае осадков, находящихся далеко от источников сноса, в кото-
рых акцессорные минералы были многократно переотложены в результате
нескольких циклов седиментации, "а также в случае весьма древних пород,
в которых первичное разнообразие акцессорных минералов уже затушевано,
получаемая информация может быть весьма незначительной. В общем аркозы
и граувакки относительно богаче акцессориями, чем субграувакки и квар-
циты как по количеству акцессориев, так и по их разнообразию. Тем
самым подтверждается известное положение, согласно которому в породах,
формировавшихся вблизи источников сноса, например в аркозах и грау-
вакках, содержится гораздо более разнообразный комплекс акцессориев,
чем в субграувакках и кварцитах, обломочный материал которых подвергался
переносу в течение длительного времени, в результате чего произошла
значительная селективная сортировка.
Следует помнить, что изменчивость минерального состава акцессориев
весьма ограничивает информацию. В наибольшей степени это ограничение
относится к породам, претерпевшим различные изменения при седиментации
и диагенезе, в результате которых изменились как первичные соотношения
между минералами, так и расположение минералов. Информация, полу-
чаемая в таких случаях, может привести к ложным выводам.
10.2. ИСТОРИЧЕСКИЙ ОБЗОР ИССЛЕДОВАНИЙ
АКЦЕССОРНЫХ МИНЕРАЛОВ
История исследований акцессорных минералов довольно детально описа-
на Босуэллом [36, гл. 11, стр. 15 и ниже], который считал, что начало ее вос-
ходит к Реомюру [346]. Когда акцессорные минералы считались еще дико-
1
Общие петрографические термины даются в понимании Крынина [268].
