Гриффитс Дж. Научные методы исследования осадочных пород

Подождите немного. Документ загружается.

102 ГЛАВА 6

со стандартами, а второго — по памяти о первом зерне и стандартах. В этом

эксперименте память начинает играть все большую роль по мере продолже-

ния эксперимента. Таким образом, желательно, чтобы в будущем просмотр

зерен в случайной последовательности при проведении аналогичных экспе-

риментов отвечал бы как схеме, так и процессу экспериментов. С другой

стороны, представляется очевидным, что такая последовательность, вероят-

но, больше способствует несовершенству эксперимента, чем любые другие

факторы; опыт, однако, является лучшим учителем (особенно ошибочный

опыт).

Смешанный эффект первого порядка «дни (последовательность) —зер-

на» оказывается незначимым, смешанный эффект «наблюдатели — дни»

и «наблюдатели — зерна»— весьма значимым. Несомненно, что результаты

измерений наблюдателями были непостоянны как от одного дня к другому,

так и от одного зерна к другому. Следовательно, по таким результатам изме-

рений давать какие-либо общие рекомендации фактически невозможно,

за исключением того, что если этот метод вообще используется, то контроль

эксперимента должен быть как-то существенно улучшен.

Тем не менее, несмотря на эти отклонения, различия, вызванные изме-

нением порядка просмотра зерен и последовательности действий наблюда-

телей, являются значительно большими, чем различия, зависящие от соот-

ветствующего смешанного эффекта. Интересно отметить, что поскольку

проверка подтверждает, что значение дисперсии «зерна — дни» близко нулю

(

= 0), основной эффект, означающий различия между зернами, может

быть проверен на взаимодействие «зерна — наблюдатели»; этот эффект

оказывается весьма значащим, т. е. он превосходит изменчивость, вызы-

ваемую взаимодействием. Такая проверка, конечно, необходима только

в случае, если от методики требуется получение информации об изменчиво-

сти формы зерен. Условия для проверки различий между наблюдателями

не столь очевидны, и хотя разница между наблюдателями заметно больше

любого взаимодействия или комбинации взаимодействий, способ проверки

остается неясным. Если исследуются различия между зернами, необходимо

выделять и учитывать эффект, обусловленный различиями между наблю-

дателями. Эти различия между наблюдателями показаны на фиг. 6.4 сплош-

ной кривой. Смешанный эффект «наблюдатели — дни» также показан,

и можно видеть, что, хотя одинаковый порядок изучения зерен обуслов-

ливает одинаковые изменения оценок исследуемых свойств, при обратном

порядке возникают значительные отклонения. Этого можно избежать при

случайном порядке изучения зерен в каждом конкретном случае.

Таблица 6.4

Результаты дисперсионного анализа округлости кварцевых

зерен из пляжных песков [364]

Источник изменчивости

Число степеней

свободы

Средний

квадрат χ 10*

Отношение

дисперсии

Зерна

14,914

28,96***

Наблюдатели

7,686 14,96***

Дни

2 0,245

<1,0

Зерна X наблюдатели

120

0,515

1,936***

Наблюдатели χ дни

0,334 1,255

Дни χ зерна

40 0,2274

0,855

Ошибка

240 0,2655

Сумма

440

1,0989

ИЗМЕРЕНИЕ ФОРМЫ ЗЕРЕН

103

0,89

Взаимодействие наблюдатели χ дни

Уровень значимости 0,05 0,01

OOl

I 0,87

S 0,88

0,81

\ /

ABCDEFG

Наблюдатель

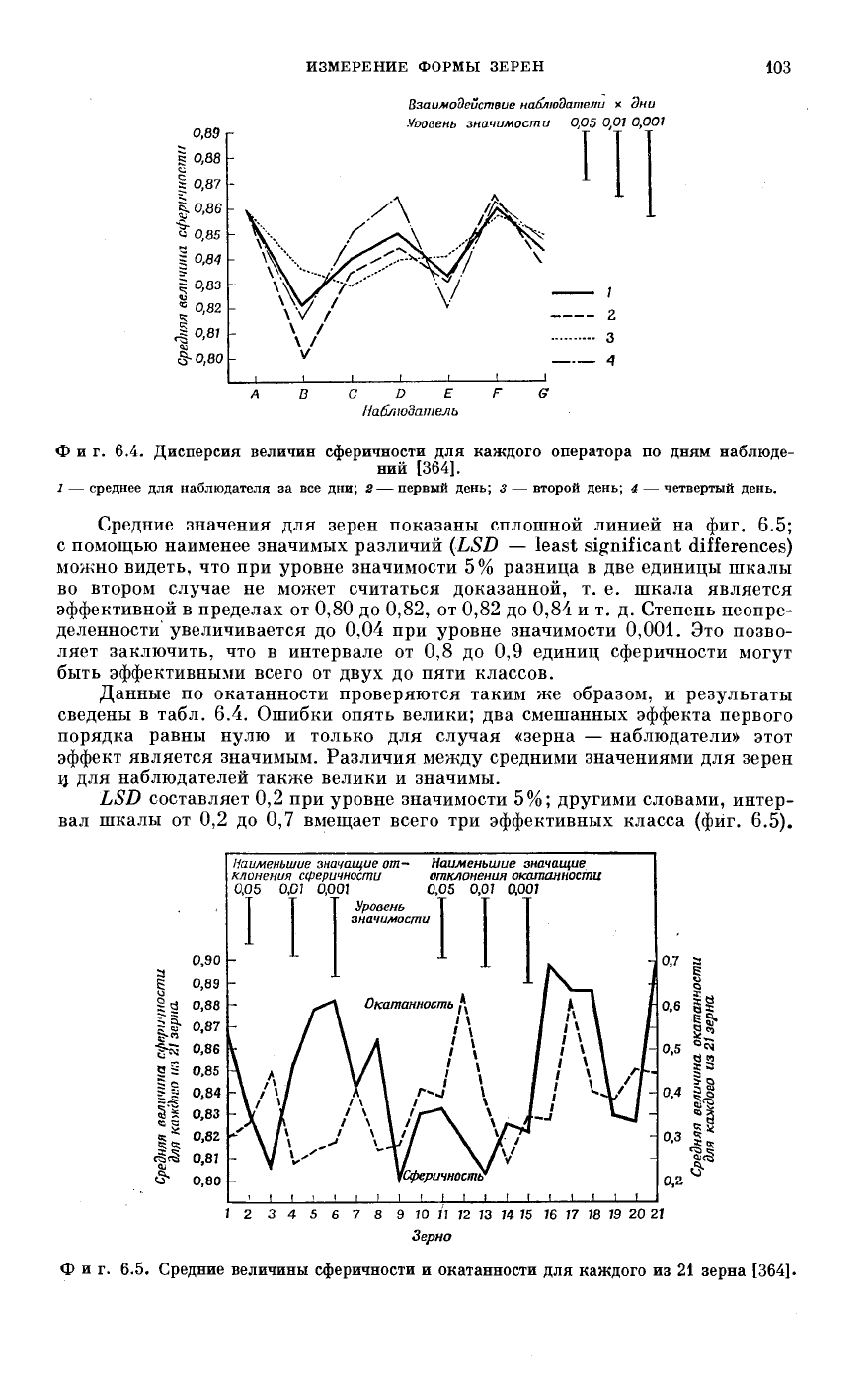
Фиг. 6.4. Дисперсия величин сферичности для каждого оператора по дням наблюде-

ний [364].

1 — среднее для наблюдателя за все дни; 2 — первый день; 3 — второй день; i — четвертый день.

Средние значения для зерен показаны сплошной линией на фиг. 6.5;

с помощью наименее значимых различий (LSD — least significant differences)

можно видеть, что при уровне значимости 5% разница в две единицы шкалы

во втором случае не может считаться доказанной, т. е. шкала является

эффективной в пределах от 0,80 до 0,82, от 0,82 до 0,84 и т. д. Степень неопре-

деленности увеличивается до 0,04 при уровне значимости 0,001. Это позво-

ляет заключить, что в интервале от 0,8 до 0,9 единиц сферичности могут

быть эффективными всего от двух до пяти классов.

Данные по окатанности проверяются таким же образом, и результаты

сведены в табл. 6.4. Ошибки опять велики; два смешанных эффекта первого

порядка равны нулю и только для случая «зерна — наблюдатели» этот

эффект является значимым. Различия между средними значениями для зерен

ц для наблюдателей также велики и значимы.

LSD составляет 0,2 при уровне значимости 5%; другими словами, интер-

вал шкалы от 0,2 до 0,7 вмещает всего три эффективных класса (фиг. 6.5).

Фиг. 6.5. Средние величины сферичности и окатанности для каждого из 21 зерна [364].

1 2 3 4 S 6 7 8 9 10 JI 12 13 14 15 16 17 18 19 20 21

Зерно

ИЗМЕРЕНИЕ ФОРМЫ ЗЕРЕН

105-

риантной к такого рода преобразованиям, и поэтому уровень полученной

информации вряд ли может достигнуть интервального (см. раздел 12.5).

Тот же эксперимент приводит нас к убеждению, что для получения

информации о форме частиц необходимо изыскивать другие, кроме указан-

ных, методы. При использовании же метода визуального сравнения програм-

ма эксперимента должна быть тщательно разработана и должен быть намечен

контроль над процессом измерений. Без соответствующих предосторожностей

дисперсия, обусловленная собственно неточностями сравнения, увеличится

за счет субъективного восприятия наблюдателя и в конечном счете влияние

неопределимых источников изменчивости, т. е. ошибок, станет весьма зна-

чительным. Большинство методов, которые основаны на использовании

способа субъективной оценки сходства со стандартами, обладают аналогич-

ными недостатками.

6.3. ИЗМЕРЕНИЯ ОТНОШЕНИЯ ОСЕЙ В ШЛИФАХ

КАК ХАРАКТЕРИСТИКИ ФОРМЫ

Другим возможным способом определения формы являются измерения,

выполняемые по двухмерным изображениям зерен в шлифах. Этот способ

особенно необходим в тех случаях, когда дезинтеграция образцов горных

пород оказывается невозможной без нарушения формы зерен. Метод может

быть аналитически выражен как

Psh

= (т, s, sh, о, ρ),

и в случае выбора одного единственного минерального компонента, скажем

кварца, состав т становится константой. Однако дальнейшее упрощение

оказывается невозможным. Когда все остальные свойства изменяются одно-

временно, изменчивость величины P

sh2

определяется влиянием четырех

главных факторов: размера s, формы sh, ориентировки зерен о и упаков-

ки р; одновременно влияние оказывают шесть смешанных эффектов первого

порядка вида s, sh; s, о и т. п.; четырех — второго порядка вида s, sh, о;

s, sh, ρ ά τ. и. я одного — третьего порядка вида s, sh, о, р. Другими сло-

вами, полученное выражение может быть записано в виде

Psh

= f(s, sh, о, р).

Ниже будут показаны трудности, связанные с вычислением величи-

ны P

; получаемые величины отражают разнородную информацию, которая

в силу своей сложности лишь отдаленно связана с понятием формы.

6.3.1. Детали методики

Помимо выбора минерального компонента, необходимо четко опреде-

лить метод выбора осей. При измерении окатанности, т. е. двухмерной сфе-

ричности, две оси могут быть выбраны способом, описанным Гриффитсо.м

и Розенфельдом [419, стр. 237]. При этом способе предусмотрено получение

изображения зерна либо путем вычерчивания его контуров с использова-

нием микропроектора, либо путем фотографирования с последующим нахо-

ждением опытным подбором наименьшего размера (ось Ъ) с помощью парал-

лельных линеек. После определения наименьшего размера проводят каса-

тельные к контуру изображения зерна под прямым углом друг к другу

и измеряют длинную ось а перпендикулярно оси Ъ, как показано на фиг. 6.7.

Если параллельные линейки снабжены еще и измерительной линейкой

с делениями в миллиметрах, размеры могут быть прочитаны сразу же после

того, как определены оси. Аналогичные наблюдения можно проводить

непосредственно под микроскопом с использованием окуляра с квадратной

104

ГЛАВА 6

Величины дисперсий, выраженные в виде стандартных отклонений,

приведены в табл. 6.5; и хотя изменчивость окатанности примерно втрое

больше сферичности, судя по разнице стандартных отклонений для зерен,

следующим наибольшим источником изменчивости оказываются ошибки,

которые также в три раза больше для оценок окатанности, чем сферичности.

Таким образом, по всей таблице результаты вполне сравнимы для обеих

переменных, т. е. изменчивость от различных причин является близкой

по своей относительной величине при обоих методах измерения.

6.2.2. Взаимоотношения между сферичностью и окатанностью

Обычно полагают, что сферичность и окатанность взаимосвязаны, однако

на основании показанного выше примера измерений 21 зерна видно, что

они не связаны [364, стр. 581]. Если определенные наблюдателем средние

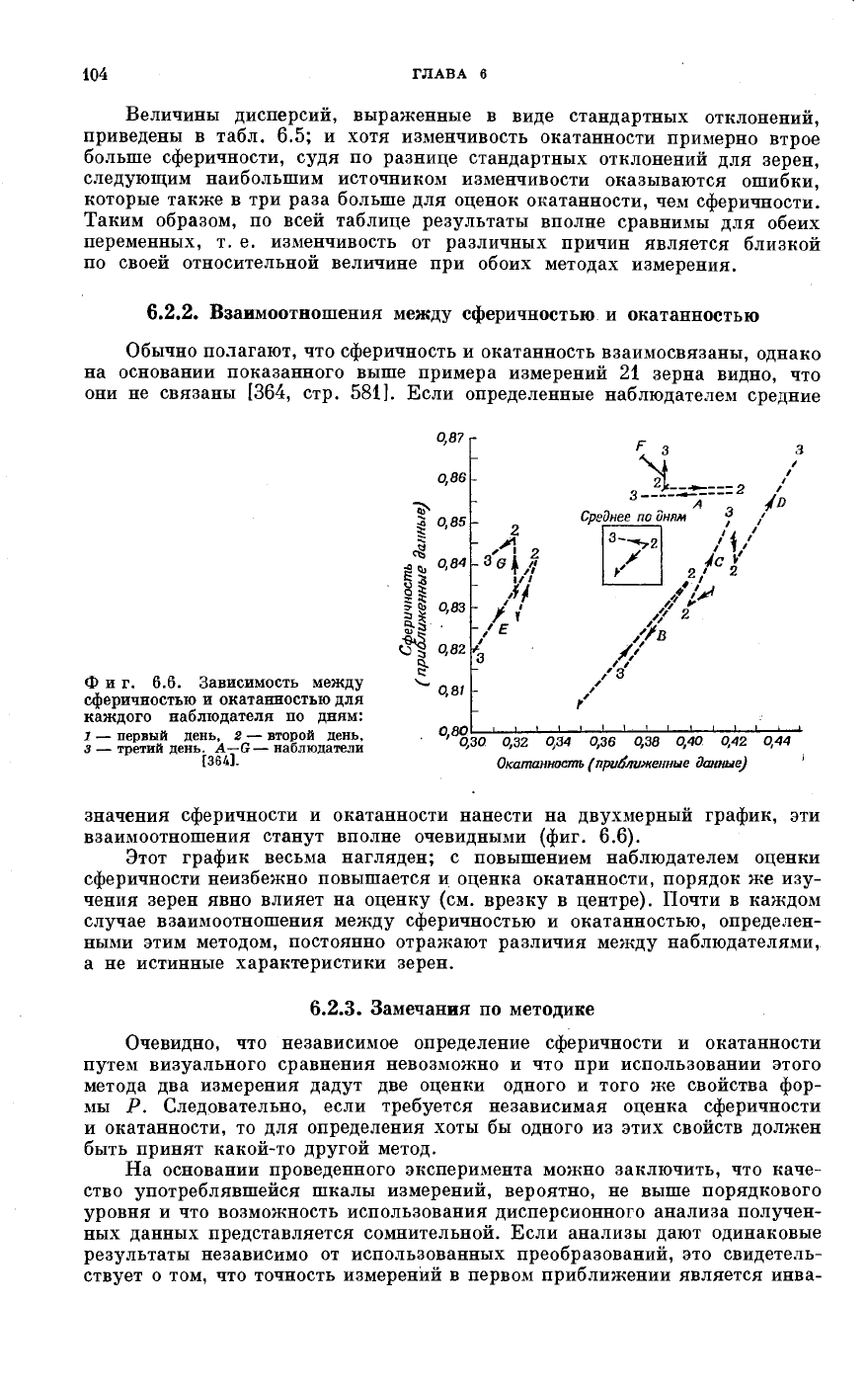
Фиг. 6.6. Зависимость между

сферичностью и окатанностью для

каждого наблюдателя по дням:

1 — первый день, 2 — второй день,

з — третий день. A-G — наблюдатели

[364].

S Ij

0,87

0,86

0,85

0,84

0,83

0,8 2

0,8/

1//

/ T

/Е

Ч.

з—--

ZZZZ 2

Среднее по дням & ,

/О

' 0,30 0,32 0,34 0,36 0,38 0,40 0,42 0,44

Окатанность (приближенные данные)

значения сферичности и окатанности нанести на двухмерный график, эти

взаимоотношения станут вполне очевидными (фиг. 6.6).

Этот график весьма нагляден; с повышением наблюдателем оценки

сферичности неизбежно повышается и оценка окатанности, порядок же изу-

чения зерен явно влияет на оценку (см. врезку в центре). Почти в каждом

случае взаимоотношения между сферичностью и окатанностью, определен-

ными этим методом, постоянно отражают различия между наблюдателями,

а не истинные характеристики зерен.

6.2.3. Замечания по методике

Очевидно, что независимое определение сферичности и окатанности

путем визуального сравнения невозможно и что при использовании этого

метода два измерения дадут две оценки одного и того же свойства фор-

мы Р. Следовательно, если требуется независимая оценка сферичности

и окатанности, то для определения хоты бы одного из этих свойств должен

быть принят какой-то другой метод.

На основании проведенного эксперимента можно заключить, что каче-

ство употреблявшейся шкалы измерений, вероятно, не выше порядкового

уровня и что возможность использования дисперсионного анализа получен-

ных данных представляется сомнительной. Если анализы дают одинаковые

результаты независимо от использованных преобразований, это свидетель-

ствует о том, что точность измерений в первом приближении является инва-

106

ГЛАВА 6

сеткой. Измерения начинают с короткой оси Ь\ при пробных экспериментах

было установлено, что в случаях, когда наблюдателям разрешалось выби-

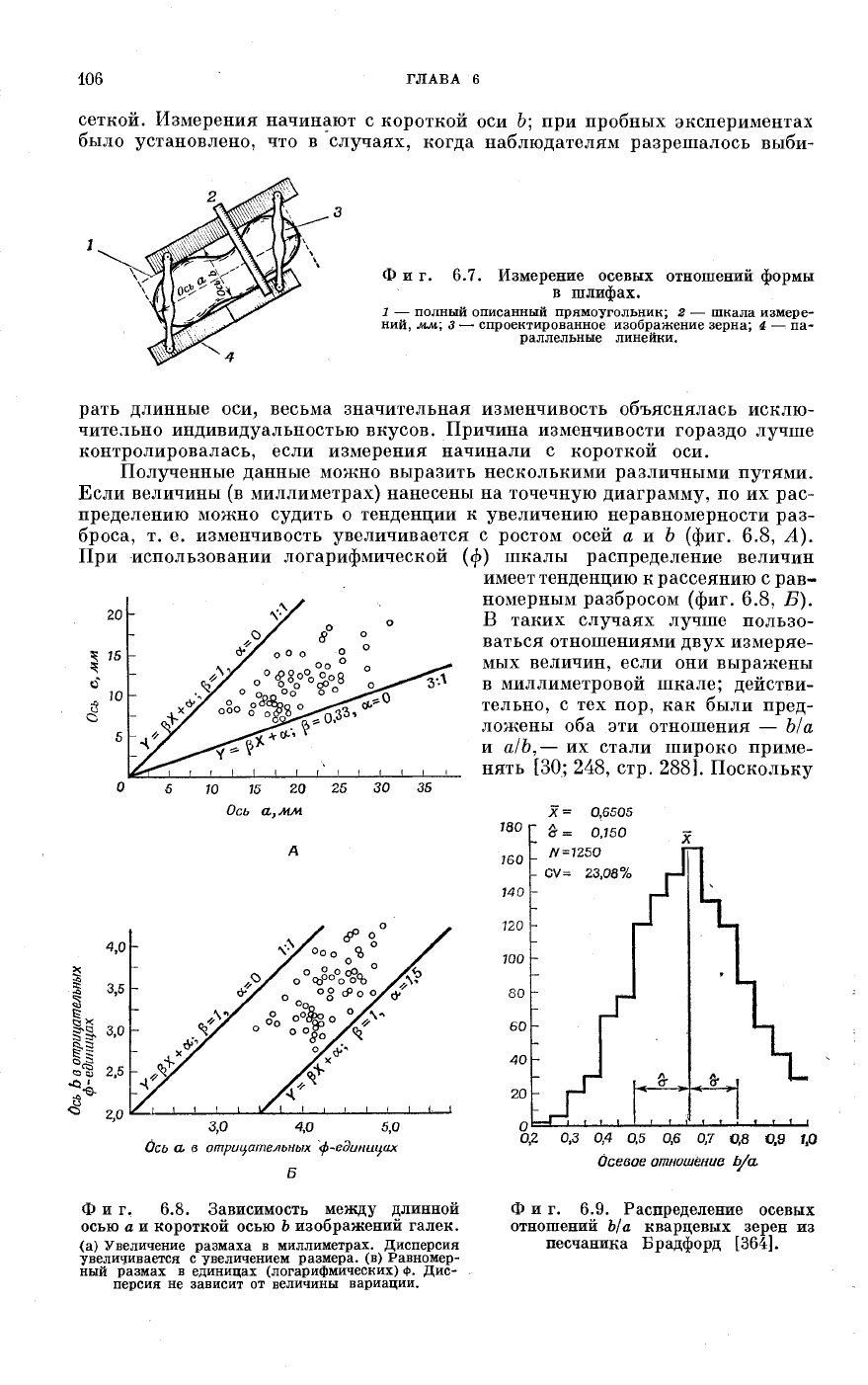
Ф и г. 6.7. Измерение осевых отношений формы

в шлифах.

1 — полный описанный прямоугольник; г — шкала измере-

ний, мм; 3 —• спроектированное изображение зерна; 4 — па-

раллельные линейки.

рать длинные оси, весьма значительная изменчивость объяснялась исклю-

чительно индивидуальностью вкусов. Причина изменчивости гораздо лучше

контролировалась, если измерения начинали с короткой оси.

Полученные данные можно выразить несколькими различными путями.

Если величины (в миллиметрах) нанесены на точечную диаграмму, по их рас-

пределению можно судить о тенденции к увеличению неравномерности раз-

броса, т. е. изменчивость увеличивается с ростом осей а и b (фиг. 6.8, А).

При использовании логарифмической (ф) шкалы распределение величин

имеет тенденцию к рассеянию с рав-

номерным разбросом (фиг. 6.8, Б).

В таких случаях лучше пользо-

ваться отношениями двух измеряе-

мых величин, если они выражены

"3·

в миллиметровой шкале; действи-

тельно, с тех пор, как были пред-

ложены оба эти отношения — Ыа

и alb,— их стали широко приме-

нять [30; 248, стр. 288]. Поскольку

¢/

?у о°Го

°°°°£°з

У ° °ЙП °

J-

Ю 15 ZO

Ось а, мм

X= 0,6505

180

Г & = 0,150

N =7250

- CV= 23,08%

!60

140 -

Ось а, в

отрицательных

ф-единицах

0,2 0,3 0,4 0,5 0,6 0,7 0,8 0,9 1,0

Осевое

отношение

Ь/а.

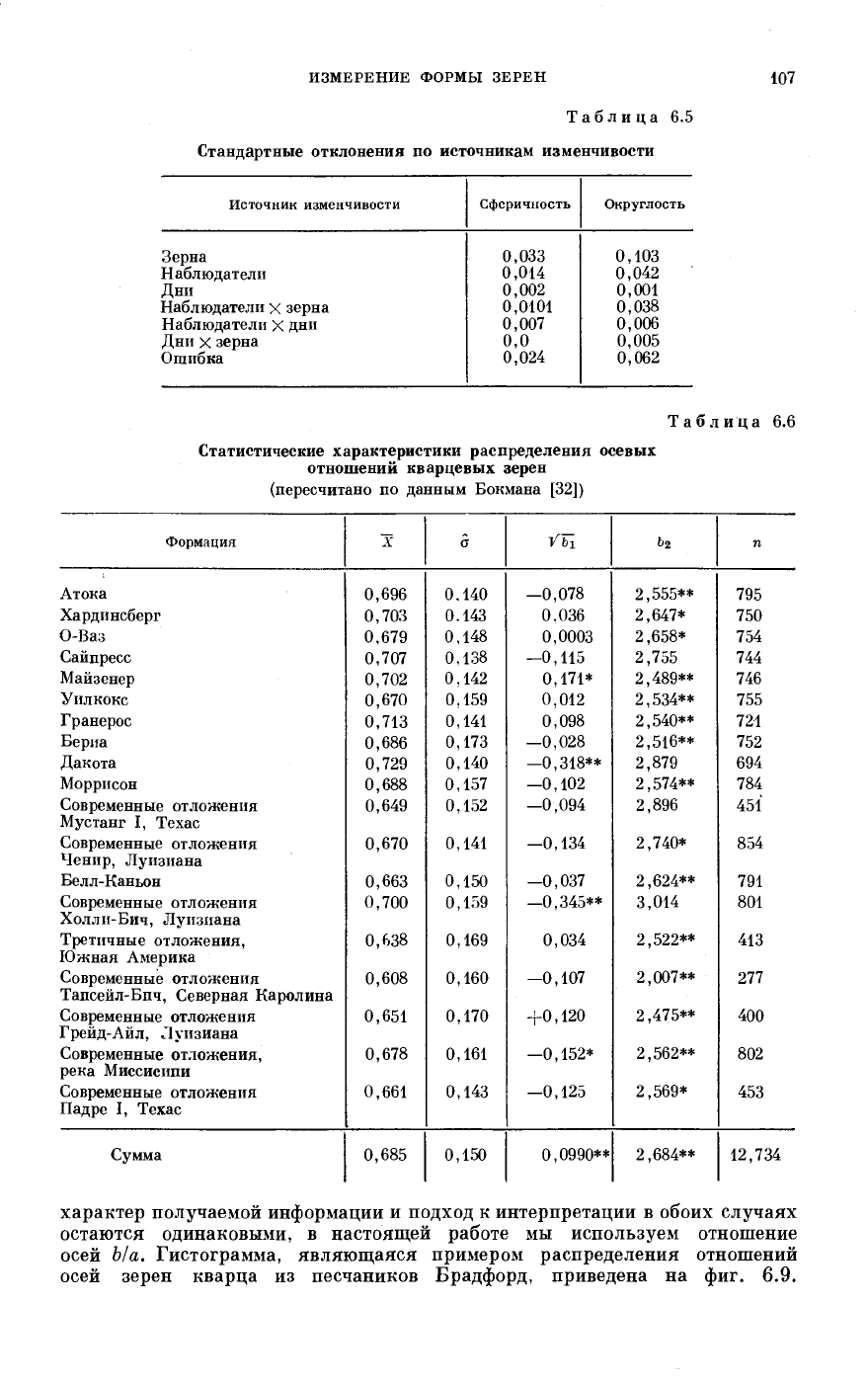
Фиг, 6.8. Зависимость между длинной

осью а и короткой осью Ь изображений галек,

(а) Увеличение размаха в миллиметрах. Дисперсия

увеличивается с увеличением размера, (в) Равномер-

ный размах в единицах (логарифмических) Ф. Дис-

персия не зависит от величины вариации.

Фиг. 6.9. Распределение осевых

отношений Ь/а кварцевых зерен из

песчаника Брадфорд [364].

ИЗМЕРЕНИЕ ФОРМЫ ЗЕРЕН 105-

Таблица 6.5

Стандартные отклонения по источникам изменчивости

Источник изменчивости

Сферичность Округлость

Зерна 0,033 0,103

Наблюдатели

0,014 0,042

Дни

0,002

0,001

Наблюдатели χ зерна

0,0101

0,038

Наблюдатели X дни

0,007 0,006

Дни χ зерна

0,0 0,005

Ошибка

0,024

0,062

Таблица 6.6

Статистические характеристики распределения осевых

отношений кварцевых зерен

(пересчитано по данным Бокмана [32])

Формация X

Vbi

Атока

0,696 0.140 —0,078

2,555**

795

Хардинсберг

0,703 0.143

0,036

2,647*

750

О-Ваз

0,679

0,148

0,0003

2,658* 754

Сайпресс

0,707

0,138

—0,115

2,755

744

Майзенер

0,702

0,142

0,171* 2,489** 746

Уилкокс

0,670 0,159 0,012

2,534**

755

Гранерос

0,713

0,141

0,098

2,540** 721

Берна

0,686

0,173

—0,028

2,516**

752

Дакота

0,729

0,140

—0,318**

2,879 694

Моррисон 0,688

0,157

-0,102

2,574**

784

Современные отложения

0,649

0,152

—0,094

2,896

451

Мустанг I, Техас

Современные отложения

0,670

0,141 -0,134 2,740* 854

Ченир, Луизиана

Белл-Каньон

0,663

0,150

—0,037

2,624**

791

Современные отложения 0,700

0,159 —0,345**

3,014

801

Холли-Бич, Луизиана

Третичные отложения,

0,638

0,169 0,034

2,522**

413

Южная Америка

0,638

Современные отложения 0,608

0,160

-0,107 2,007**

277

Тапсейл-Бпч, Северная Каролина

Современные отложения

0,651

0,170

-f0,120

2,475**

400

Грейд-Айл, Луизиана

Современные отложения,

0,678 0,161

—0,152*

2,562**

802

река Миссисипи

Современные отложения 0,661 0,143 —0,125

2,569*

453

Падре I, Техас

Сумма 0,685 0,150 0,0990**

2,684**

12,734

характер получаемой информации и подход к интерпретации в обоих случаях

остаются одинаковыми, в настоящей работе мы используем отношение

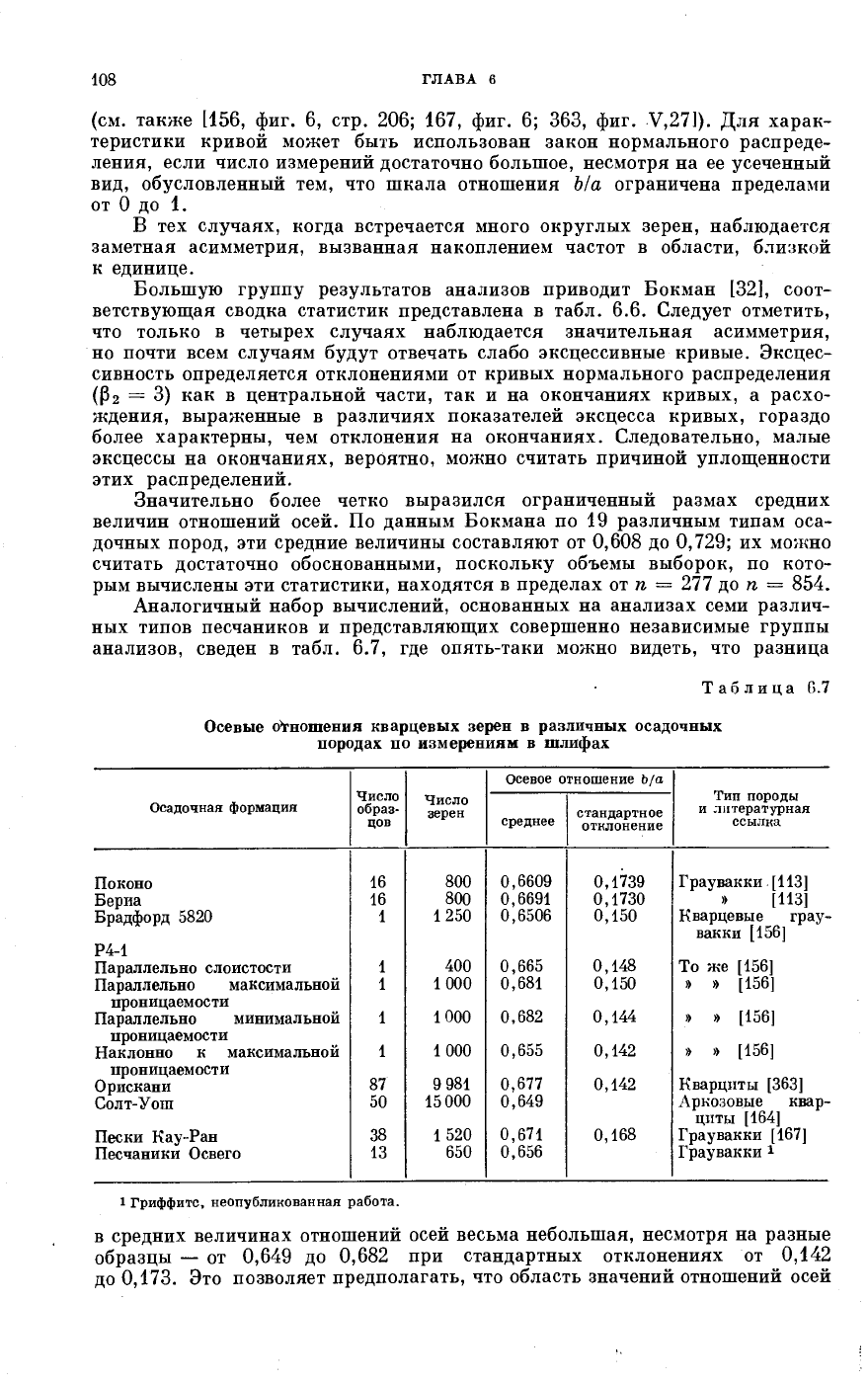
осей Ыа. Гистограмма, являющаяся примером распределения отношений

осей зерен кварца из песчаников Брадфорд, приведена на фиг. 6.9.

108

ГЛАВА 6

(см. также [156, фиг. 6, стр. 206; 167, фиг. 6; 363, фиг. V,27]). Для харак-

теристики кривой может быть использован закон нормального распреде-

ления, если число измерений достаточно большое, несмотря на ее усеченный

вид, обусловленный тем, что шкала отношения Ыа ограничена пределами

от 0 до 1.

В тех случаях, когда встречается много округлых зерен, наблюдается

заметная асимметрия, вызванная накоплением частот в области, близкой

к единице.

Большую группу результатов анализов приводит Бокман [32], соот-

ветствующая сводка статистик представлена в табл. 6.6. Следует отметить,

что только в четырех случаях наблюдается значительная асимметрия,

но почти всем случаям будут отвечать слабо эксцессивные кривые. Эксцес-

сивность определяется отклонениями от кривых нормального распределения

(β2 = 3) как в центральной части, так и на окончаниях кривых, а расхо-

ждения, выраженные в различиях показателей эксцесса кривых, гораздо

более характерны, чем отклонения на окончаниях. Следовательно, малые

эксцессы на окончаниях, вероятно, можно считать причиной уплощенности

этих распределений.

Значительно более четко выразился ограниченный размах средних

величин отношений осей. По данным Бокмана по 19 различным типам оса-

дочных пород, эти средние величины составляют от 0,608 до 0,729; их можно

считать достаточно обоснованными, поскольку объемы выборок, по кото-

рым вычислены эти статистики, находятся в пределах от η = 277 до η = 854.

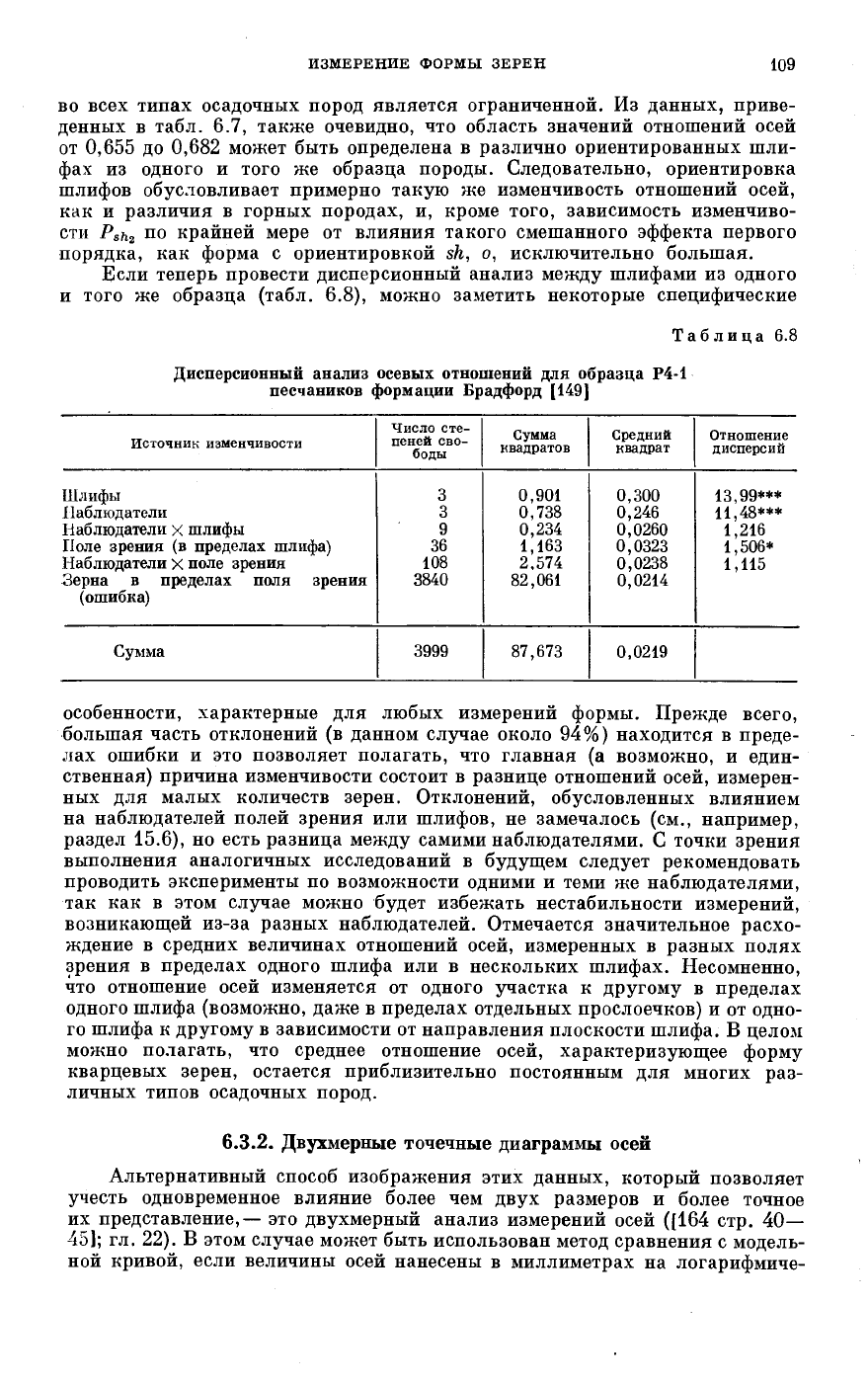
Аналогичный набор вычислений, основанных на анализах семи различ-

ных типов песчаников и представляющих совершенно независимые группы

анализов, сведен в табл. 6.7, где опять-таки можно видеть, что разница

Таблица 0.7

Осевые отношения кварцевых зерен в различных осадочных

породах по измерениям в шлифах

Осадочная формация

Число

образ-

цов

Число

зерен

Осевое отношение Ь/а

Тип породы

и литературная

ссылка

Осадочная формация

Число

образ-

цов

Число

зерен

среднее

стандартное

отклонение

Тип породы

и литературная

ссылка

Поконо

800

0,6609

0,1739 Граувакки [113]

Бериа

800

0,6691

0,1730

» [113]

Брадфорд 5820

1250

0,6506

0,150 Кварцевые грау-

вакки [156]

Р4-1

Параллельно слоистости

400

0,665 0,148

То же [156]

Параллельно максимальной

1000

0,681

0,150

» » [156]

проницаемости

1000

0,682

0,144 » » [156]

Параллельно минимальной

1 1000

0,682

0,144 » » [156]

проницаемости

1000

0,655

0,142

» » [156]

Наклонно к максимальной

1000

0,655

0,142

» » [156]

проницаемости

9 981 0,677

0,142 Кварциты [363]

Орискани

9 981 0,677

0,142 Кварциты [363]

Солт-Уош

15000 0,649

Аркозовые квар-

циты [164]

Пески Кау-Ран

1520

0,671

0,168 Граувакки [167]

Песчаники Освего

650

0,656 Граувакки

ι Гриффите, неопубликованная работа.

в средних величинах отношений осей весьма небольшая, несмотря на разные

образцы — от 0,649 до 0,682 при стандартных отклонениях от 0,142

до 0,173. Это позволяет предполагать, что область значений отношений осей

ИЗМЕРЕНИЕ ФОРМЫ ЗЕРЕН

105-

во всех типах осадочных пород является ограниченной. Из данных, приве-

денных в табл. 6.7, также очевидно, что область значений отношений осей

от 0,655 до 0,682 может быть определена в различно ориентированных шли-

фах из одного и того же образца породы. Следовательно, ориентировка

шлифов обусловливает примерно такую же изменчивость отношений осей,

как и различия в горных породах, и, кроме того, зависимость изменчиво-

сти P

sh2

по крайней мере от влияния такого смешанного эффекта первого

порядка, как форма с ориентировкой sh, о, исключительно большая.

Бели теперь провести дисперсионный анализ между шлифами из одного

и того же образца (табл. 6.8), можно заметить некоторые специфические

Таблица 6.8

Дисперсионный анализ осевых отношений для образца Р4-1

песчаников формации Брадфорд [149]

Источник изменчивости

Число сте-

пеней сво-

боды

Сумма

квадратов

Средний

квадрат

Отношение

дисперсий

Шлифы 3

0,901 0,300

13,99***

Наблюдатели 3 0,738

0,246

11,48***

Наблюдатели χ шлифы

9 0,234

0,0260 1,216

Поле зрения (в пределах шлифа)

1,163 0,0323

1,506*

Наблюдатели χ поле зрения

108

2,574 0,0238

1,115

Зерна в пределах поля зрения

(ошибка)

3840 82,061 0,0214

Сумма

3999

87,673 0,0219

особенности, характерные для любых измерений формы. Прежде всего,

большая часть отклонений (в данном случае около 94%) находится в преде-

лах ошибки и это позволяет полагать, что главная (а возможно, и един-

ственная) причина изменчивости состоит в разнице отношений осей, измерен-

ных для малых количеств зерен. Отклонений, обусловленных влиянием

на наблюдателей полей зрения или шлифов, не замечалось (см., например,

раздел 15.6), но есть разница между самими наблюдателями. С точки зрения

выполнения аналогичных исследований в будущем следует рекомендовать

проводить эксперименты по возможности одними и теми же наблюдателями,

так как в этом случае можно будет избежать нестабильности измерений,

возникающей из-за разных наблюдателей. Отмечается значительное расхо-

ждение в средних величинах отношений осей, измеренных в разных полях

зрения в пределах одного шлифа или в нескольких шлифах. Несомненно,

что отношение осей изменяется от одного участка к другому в пределах

одного шлифа (возможно, даже в пределах отдельных прослоечков) и от одно-

го шлифа к другому в зависимости от направления плоскости шлифа. В целом

можно полагать, что среднее отношение осей, характеризующее форму

кварцевых зерен, остается приблизительно постоянным для многих раз-

личных типов осадочных пород.

6.3.2. Двухмерные точечные диаграммы осей

Альтернативный способ изображения этих данных, который позволяет

учесть одновременное влияние более чем двух размеров и более точное

их представление,— это двухмерный анализ измерений осей ([164 стр. 40—

45]; гл. 22). В этом случае может быть использован метод сравнения с модель-

ной кривой, если величины осей нанесены в миллиметрах на логарифмиче-

110

ГЛАВА 6

скую бумагу или после перевода этих величин в ф-единицы — на милли-

метровку. В первом случае, когда зерна или их изображения имеют округлую

форму, оси а и

примерно равны и для обеих осей координат использован

одинаковый масштаб, точки будут ложиться на прямую линию, которая

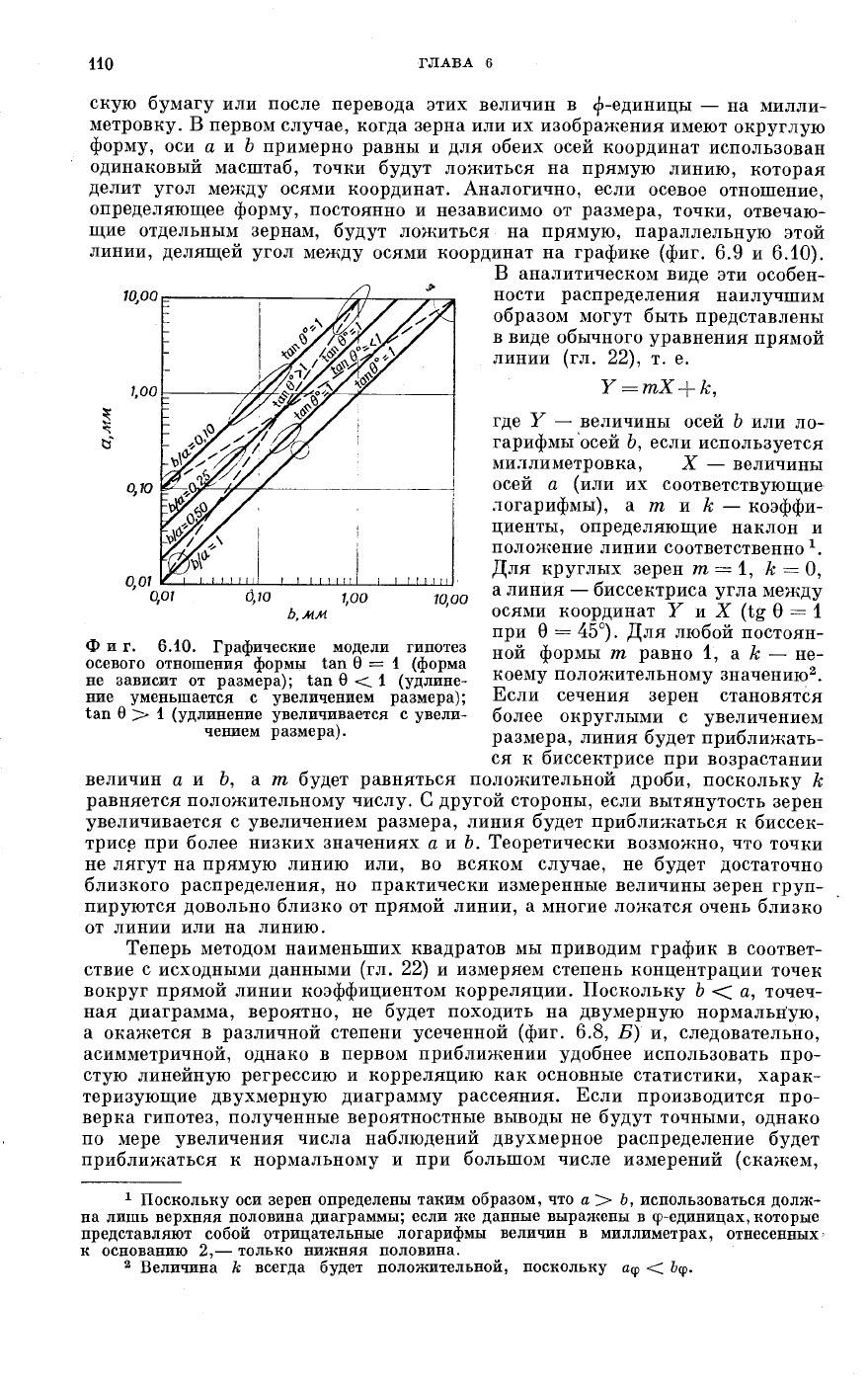
делит угол между осями координат. Аналогично, если осевое отношение,

определяющее форму, постоянно и независимо от размера, точки, отвечаю-

щие отдельным зернам, будут ложиться на прямую, параллельную этой

линии, делящей угол между осями координат на графике (фиг. 6.9 и 6.10).

В аналитическом виде эти особен-

ности распределения наилучшим

образом могут быть представлены

в виде обычного уравнения прямой

линии (гл. 22), т. е.

Y = mX + k,

где Y — величины осей Ъ или ло-

гарифмы осей 6, если используется

миллиметровка, X — величины

осей а (или их соответствующие

логарифмы), а т и к — коэффи-

циенты, определяющие наклон и

положение линии соответственно Ч

Для круглых зерен т — 1, к = 0,

а линия — биссектриса угла между

осями координат Y и X (tg 0 = 1

при θ = 45°). Для любой постоян-

ной формы т равно 1, а к — не-

коему положительному значению

Если сечения зерен становятся

более округлыми с увеличением

размера, линия будет приближать-

ся к биссектрисе при возрастании

величин а и Ъ, а т, будет равняться положительной дроби, поскольку к

равняется положительному числу. С другой стороны, если вытянутость зерен

увеличивается с увеличением размера, линия будет приближаться к биссек-

трисе при более низких значениях а и Ъ. Теоретически возможно, что точки

не лягут на прямую линию или, во всяком случае, не будет достаточно

близкого распределения, но практически измеренные величины зерен груп-

пируются довольно близко от прямой линии, а многие ложатся очень близко

от линии или на линию.

Теперь методом наименьших квадратов мы приводим график в соответ-

ствие с исходными данными (гл. 22) и измеряем степень концентрации точек

вокруг прямой линии коэффициентом корреляции. Поскольку

<; а, точеч-

ная диаграмма, вероятно, не будет походить на двумерную нормальную,

а окажется в различной степени усеченной (фиг. 6.8, Б) и, следовательно,

асимметричной, однако в первом приближении удобнее использовать про-

стую линейную регрессию и корреляцию как основные статистики, харак-

теризующие двухмерную диаграмму рассеяния. Если производится про-

верка гипотез, полученные вероятностные выводы не будут точными, однако

по мере увеличения числа наблюдений двухмерное распределение будет

приближаться к нормальному и при большом числе измерений (скажем,

Поскольку оси зерен определены таким образом, что а > Ъ, использоваться долж-

на лишь верхняя половина диаграммы; если же данные выражены в φ-единицах, которые

представляют собой отрицательные логарифмы величин в миллиметрах, отнесенных

к основанию 2,— только нижняя половина.

Величина к всегда будет положительной, поскольку α

< 6φ.

Фиг. 6.10. Графические модели гипотез

осевого отношения формы tail 6=1 (форма

не зависит от размера); tan Ocl (удлине-

ние уменьшается с увеличением размера);

tan θ > 1 (удлинение увеличивается с увели-

чением размера).

ИЗМЕРЕНИЕ ФОРМЫ ЗЕРЕН

105-

более 100) результаты не будут содержать серьезной ошибки. Арифметиче-

ские и логарифмкческие выражения мы можем суммировать и сравнить

в следующем виде.

Выражение осевых отношений кварцевых зерен, измеренных в шлифах

ОТНОШЕНИЯ ОСЕЙ, ОПРЕДЕЛЯЮЩИЕ ФОРМУ

а—длинная ось; Ioga = X.

b—короткая ось; Iogb = Y.

Форма выражения в

миллиметрах логарифмах

= кат Y = к' -\-тХ

Первый случай. Если т.= 1 (форма постоянна при любых размерах)

= ка, Y = k' + lX.

Второй случай: Если т < 1, например т = 2 (форма изменяется, вытянутость увеличи-

вается с увеличением размера)

ка*,

y=fc'+2X.

Третий случай. Если т<1, например т= 1/2 (форма изменяется, округлость увеличи-

вается с увеличением размера)

= ка

1/2

= кУа, У =

Теперь мы можем построить модели, являющиеся гипотезами, предназначенными для

проверки.

Гипотеза. H

; форма в ψ-единпцах Y = βχ ^a

Для постоянной округлой формы β =

и а =

Для постоянной формы β=1 и а = положительное значение

Для округлости, увеличивающейся с размером, β<1·

Для вытянутости, увеличивающейся с размером, β>1·

Критерием для проверки H

является величина (β—т)/а

, которая ^-распределена по

закону Стьюдента с η—2 степенями свободы.

В качестве примера рассмотрим точечную диаграмму на фиг. 6.11, где

показан график средних значений осей Ъ и а, выраженных в ф-единицах,

определенных для кварцевых зерен из 50 образцов песчаников Солт-Уош [164,

фиг. на стр. 40, и фиг. 11.8]. Совершенно очевидно, что расположение точек

близко к прямолинейному и рассеяние является весьма малым, как видно

и по коэффициенту корреляции г = 0,99. Зависимость для 25 рудоносных

образцов будет Y = 1,0535 X + 0,4685 и гипотеза β = 1 не отвергается;

следовательно, эта зависимость приблизительно может быть выражена как

Y = X + 0,4685.

В работе [164] величина отношения b к а в миллиметрах вычислена как

0,649. Не менее интересен вопрос, каким образом связь между осями ста-

билизируется в зависимости от усреднения? В табл. 6.9 степень зависимости

Таблица 6.9

Зависимость между осями а и 6 кварцевых зерен,

измеренными в шлифах песчаников Солт-Уош

Число

образцов

Источник изменчивости

Коэффициент корреляции

Число

образцов

Источник изменчивости

рудные

породы

безрудные

7500

Среднее для образцов

Среднее для поля зрения

Среднее для зерен

Вся совокупность

0,9931

0,8049

0,7697

0,7490

0,9927

0,8171

0,5369

0,7325