Гриффитс Дж. Научные методы исследования осадочных пород

Подождите немного. Документ загружается.

ГЛАВА 6

5.5. ПРИМЕРЫ РАСПРЕДЕЛЕНИИ РАЗМЕРОВ ЗЕРЕН

Размер частиц агрегата, например осадочных пород, выражается числом

на какой-то шкале, но, как уже упоминалось, различные способы опреде-

ления размеров приводят к различным значениям, причем в разных способах

применяются разные шкалы. Поэтому необходимо с самого начала иметь

в виду, что разными способами получают разную информацию — одну более,

другую менее точно и ясно интерпретируемую. При так называемых «кос-

венных» способах измерения зерен поликомпонентного агрегата в лучшем

случае достигается порядковый уровень информации. В этом случае целе-

сообразно применять порядковые статистики. При измерениях в шлифах

получают значения интервальной шкалы а при прямых измерениях можно

получить значения шкалы отношений.

Для характеристики распределения размеров зерен обычно используют

модель логнормального распределения [247]. Несмотря на существующие

противоречия относительно возможности применения этой модели, она пред-

ставляется наилучшим приближением к выяснению распределения как

с теоретических, так и с экспериментальных позиций (см., например,

гл. 13.12). Чтобы добиться картины нормального распределения, нужно

изучаемую переменную (размер зерна) выразить в значениях ф-шкалы,

провести правильный отбор образцов и выполнить измерения в строго уста-

новленном порядке [176]. Любое отклонение от этих рекомендаций приведет

к отклонению от модели. Например, логарифмы радиусов апельсинов данного

сорта могли бы быть нормальными, но если апельсины разных сортов пере-

мешаны, общее распределение почти наверняка будет полимодальным.

Если, кроме того, добавить к апельсинам несколько бананов, распределение

будеа· меняться почти бессистемно: здесь будет меняться форма, размер

и состав, и эти изменения выразятся в так называемых «измерениях» раз-

меров. Полную аналогию с этим примером являют собой осадочные породы

или любые другие поликомпонентные агрегаты. При последующем рассмо-

трении за основу будет принята логнормальная модель; отклонения от нее

объясняются различными способами определений и нарушениями условий

случайного опробования. Чтобы статистики имели смысл, нужно проверить

их значимость, но если такая проверка невозможна, нельзя будет добиться

и физической интерпретации их изменчивости. По непроверенным статисти-

кам можно сделать лишь смутные неопределенные заключения. При при-

менении таких статистик, как порядковые статистики, медианы, квартили

и квантили, с помощью которых сравниваются разные системы, исходят

из нормальной модели распределения [133, 214, 291, 292]. В общем нельзя

характеризовать статистики, если мы не отнесли их κ какой-либо известной

модели распределения.

Нормальная модель распределения размеров в ф-единицах дает воз-

можность использовать оценки моментов как подходящих обобщающих

статистик. На нижеследующих страницах оценки четырех моментов будут

соответствовать параметрам: неизвестному среднему μ, дисперсии σ

или

стандартному отклонению σ и пирсоновским бета-величинам: Vfii как

мере асимметрии и β

как мере эксцесса кривой. Соответствующими статисти-

ческими оценками этих параметров являются Χ, σ

, σ, Vb

и b

. Прежде

всего следует начать с проверки значимости оценок β-величин. Известно,

что при нормальном распределении Vp

= 0, a Vfi

= 3. Отклонения

от этих параметрических значений, возникающие из-за ошибок опробова-

ния, приведены в таблицах (например, в работе [323], табл. 34, b и 34, с,

О терминах см. гл. 12.5.

ПРЕДСТАВЛЕНИЕ РЕЗУЛЬТАТОВ ИЗМЕРЕНИЙ

стр. 183—184), по которым легко найти значимость оценок Ь

парамет-

ров β, для любых размеров зерен.-Гриффите [162] и Мильнер [300] исполь-

зовали статистики g

для оценки параметров y

по Фишеру.

5.6. РАСПРЕДЕЛЕНИЕ РАЗМЕТОВ

ПО КОСВЕННЫМ СПОСОБАМ ИЗМЕРЕНИЙ

Определяя размеры зерен методом пипетки или просеивания, мы

получаем независимую переменную X (логарифм или ф-эквивалент изме-

ренных значений) и Зависи-

SOO t-

аоо

7OO

600 -

SOO

I 400

^ 300

2OO -

- 99%-ныи доверитель-

ный интервал (.включа-

ющий Щ7% площади

нормального распреде-

ления)

От -3,99 до ΙΟββ

ф-единиц

X = 3,3385 φ

& =2,4415 φ

Sk = 0,0034

К = 2,2406

g·, = 0,0169

ffz = 2,2431

CV = 73,73

N =6976 %

Очень

тонкий лесок

0,0168

= 5,2406

100

Нормальное

распределение

-B

O -4,0 -2,0 О 2,0 4,0 6,0 8.0 IOft 72,0

мую переменную, или часто-

ту встречаемости Y (обычно

в весовых процентах). Раз-

мер выражается как P =

= /

(τη,

s, sh), и среднее значе-

ние представляет средний

размер зерен одного грамма

осадочной породы. Искусст-

венная мера (весовые процен-

ты), в которой выражаются

результаты опытов, не дает

возможности использовать их

как собственно размеры зе-

рен. Из-за неопределенности

объема выборки η трудно

использовать понятие числа

степеней свободы и нельзя

проверить значимость стати-

стических характеристик.

Поэтому получаемые здесь

«статистические оценки» не

отчетливы. Пытались эмпи-

рически интерпретировать

изменчивость оценок асим-

метрии и эксцесса. Резуль-

таты экспериментов настоль-

ко неясны, что вряд ли

оправдывается стоимость по-

следних. Такого рода недо-

статки относятся к любому

косвенному способу опреде-

ления размера частиц поликомпонентных систем, с помощью которого

хотели осуществлять геологическую и генетическую интерпретацию.

Тем не менее указанные способы широко применяются при изучении

размеров и сортировке зерен. Недостатки их пытались восполнить приме-

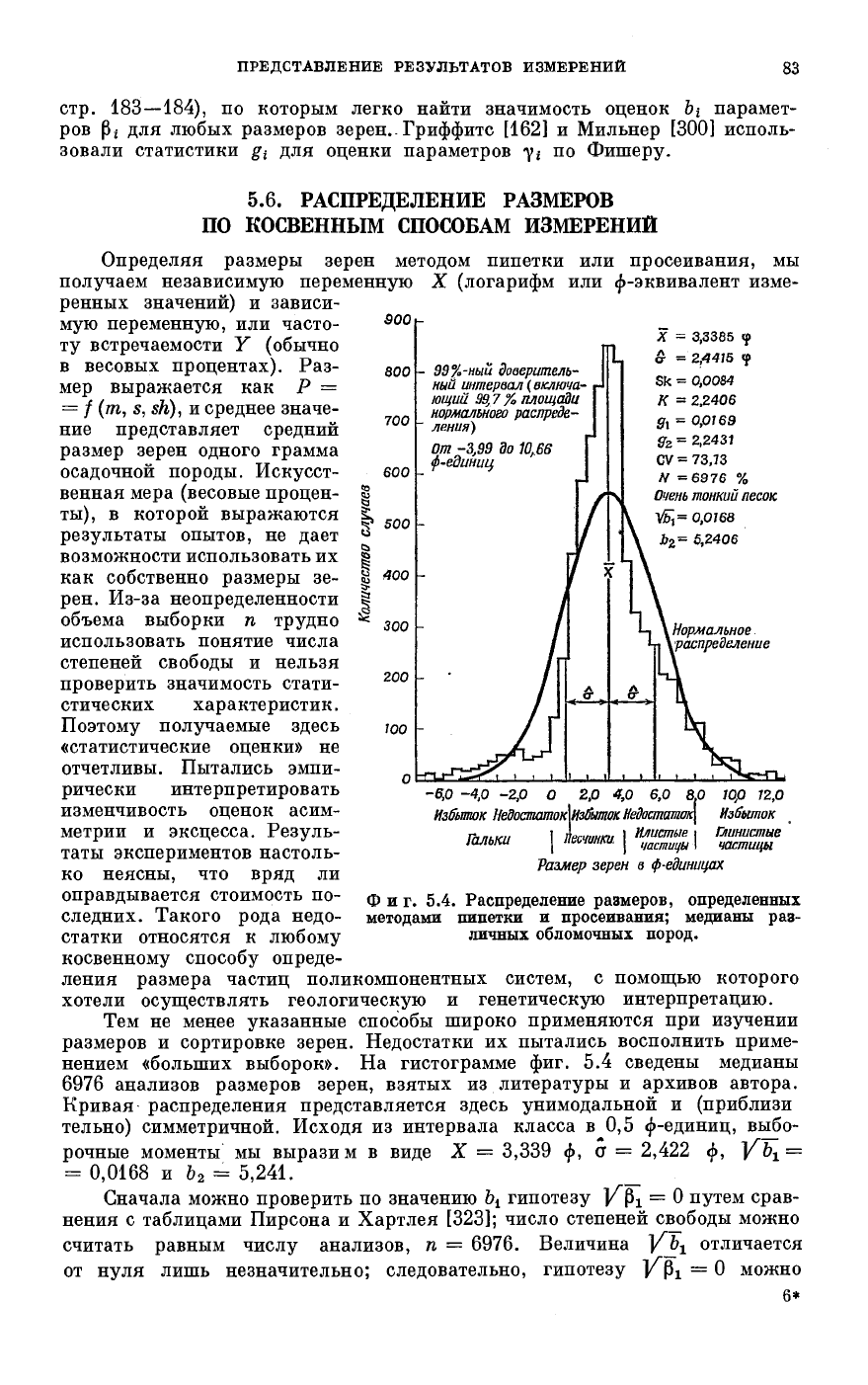
нением «больших выборок». На гистограмме фиг. 5.4 сведены медианы

6976 анализов размеров зерен, взятых из литературы и архивов автора.

Кривая распределения представляется здесь унимодальной и (приблизи

тельно) симметричной. Исходя из интервала класса в 0,5 ф-единиц, выбо-

рочные моменты мы выразим в виде X = 3,339 ф, а = 2,422 ф, Yb

= 0,0168 и Ъ

= 5,241. _

Сначала можно проверить по значению гипотезу Yfi

= 0 путем срав-

нения с таблицами Пирсона и Хартлея [323]; число степеней свободы можно

считать равным числу анализов, η = 6976. Величина Yb

отличается

от нуля лишь незначительно; следовательно, гипотезу Yft

= 0 можно

"»

v u

Избыток Иедастатоц

Избыток

Избыток Недостаток

Гальки

Размер зерен в ф-един/щах

ргттт I

ИЛистЫВ

I ШниСПШв

1 починки

частицы

I частицы

Фиг. 5.4. Распределение размеров, определенных

методами пипетки и просеивания; медианы раз-

личных обломочных пород.

ГЛАВА 6

принять и кривую распределения считать симметричной. Коэффициент

эксцесса, оценивающийся как Ъ

= 5,241, является вполне значимым и кри-

вая резко пикообразной, т. е. гипотеза V^

= 3 отклоняется и принимается

|/"β

φ 3, что не отвечает нормальной модели. Теперь необходимо рассмо-

треть природу отклонений от этой модели. Для этой цели рассчитана нор-

мальная кривая с параметрами μ = 3,339 ист = 2,442 (гл. 13.5). Эта нор-

мальная кривая накладывается на гистограмму фиг. 5.4. Затем отклонения

по классам между наблюдаемой гистограммой и теоретической нормальной

кривой проверяются по методу хи-квадрат (гл. 17.4) и они, конечно, оказы-

ваются вполне значимыми. Для классов ниже 10, ниже —2 и между 1 и 4

ф-единицами наблюдается избыток наблюдаемых значений по сравне-

нию с ожидаемыми, а для классов от 1 до —2 от 4 до 10 ф-единиц — недо-

статок.

Имеется много возможных объяснений для этих расхождений. Пред-

полагается, например, что есть недостаток мелких галек среди частиц оса-

дочных пород [329, стр. 47], чем и можно объяснить дефицит в интервале

от 1 до —2 ф-единиц. Наиболее примечательно то, что дефицит приходится

также на частички пылеватых размеров (от 4 до 8 ф, или от 62,5 до 3,9 мк),

которые изобилуют в осадочных породах. Избыток глинистых, песчаных

и грубых гравийных частиц скорее всего объясняется применением спе-

циальных методик (рентгеноскопического анализа, изучения с помощью

микроскопа и отдельных мегаскопических наблюдений). В то же время

частицы промежуточного размера, т. е. находящиеся между теми, которые

определяются рентгеноскопически и оптически, а также между теми, кото-

рые выявляются оптически и мегаскопически, могут выпасть из поля зрения

исследователей. Если это объяснение справедливо, смещение, выраженное

в форме кривой, должно обусловливаться селективностью работы оператора,

а не ненормальным характером распределения. В настоящее время такое

объяснение представляется наиболее приемлемым. Очевидно также, что,

имея в виду подобное объяснение, нет смысла увеличивать число анализов,

так как это приведет к еще большему искажению формы (степени пико-

образности) кривой и увеличению смещения.

Таким образом,. основываясь на умеренно больших выборках, можно

заключить, что распределение медианных размеров зерен в пробах осадоч-

ных пород, в которых размеры зерен определены косвенными методами,

будет близко к логнормальному. Поэтому среднее арифметическое X пред-

ставляет собой несмещенную оценку среднего арифметического генеральной

совокупности μ всех обломочных пород. Следовательно, значение μ близко

к 3,339 ф-единицы, чему соответствует ~100 мк

. Отсутствие асимметрии

указывает на то, что увеличение размера проб существенно не изменит ука-

занных значений. С другой стороны, оценка стандартного отклонения

является, по всей вероятности, заниженной, так как на ошибки оценки

дисперсии сильно влияют отклонения четвертого момента. Тем не менее,

если мы примем за основу указанное значение, сможем считать, что μ ± 3σ

дает интервал размеров от —3,99 до 10,66 ф-единиц (приблизительно

от 8 мм до 0,5 мк) и что примерно 3 медианы из каждой тысячи будут выпа-

дать из этого интервала (99,7% площади нормальной кривой включается

в интервал, равный ±3σ относительно среднего; гл. 13.7). Таким образом,

намечается возможное приближение к выяснению распределения размеров

также и в тех случаях, когда размер определен по способу осаждения в пипет-

ке или просеивания.

Заметим, что среднее геометрическое не совпадает С оценкой среднего значения

величины^ х, а является медианой.— Прим. ред.

ПРЕДСТАВЛЕНИЕ РЕЗУЛЬТАТОВ ИЗМЕРЕНИЙ

5.7. РАСПРЕДЕЛЕНИЕ РАЗМЕРОВ ПРИ ОПРЕДЕЛЕНИИ ИХ В ШЛИФАХ

Определение размеров в шлифах значительно отличается от опреде-

лений косвенными способами как по природе изучаемой независимой пере-

менной — видимой длины (или сечения), так и по природе зависимой пере-

менной, которая обычно выражается частотой. Независимая переменная,

видимая длина, может быть определена как P = / (s, sh, о, р). Эта мера

содержит очень сложную информацию об изменении размера, формы, ориен-

тировки и упаковки (степени плотности заполнения пространства зернами)

и различных взаимодействий этих факторов. Эту меру трудно истолковать

относительно собственно размера зерен. Несмотря на то что она, по-види-

мому, и имеет более прямое отношение к размеру, чем переменные, полу-

ченные при косвенных способах, все же уровень информации, заключенной

в этой мере, вряд ли окажется выше интервального. С другой стороны, объем

выборки η здесь строго определен и при проверке гипотез легко использо-

вать понятие числа степеней свободы.

Можно использовать эмпирический подход для оценки результатов

этого метода, так как имеется богатый справочный материал о таких ана-

лизах. Результаты анализов оказываются вполне согласующимися с теми,

которые получены другими методами, хотя эти результаты несколько отли-

чаются одни от других вследствие различной процедуры анализов. Очень

важно знать пределы размеров зерен для данного метода. С одной стороны,

измерять зерна диаметром меньше 5 ф-единиц (31,2 мк) чрезвычайно трудно,

так как при наличии матрицы мелкие зерна почти не выделяются. С другой

стороны, размер зерен может значительно превышать поле зрения микро-

скопа, что влечет за собой другие затруднения при измерениях. Для зерен

кварца размером со среднюю песчинку этот способ прост и эффективен.

Некоторые его ограничения описаны в литературе [57, 58, 63, 64, 112,

136, 241].

В данном случае также можно подойти к вопросу с точки зрения боль-

ших выборок. Примером такого рода служит изучение осадочной породы

пачки Солт-Уош формации Мбррисон (плато Колорадо) [164]. Тремя опера-

торами (вернее, тремя группами операторов по 5 человек в каждой) здесь

было выполнено около 16 ООО измерений осей зерен кварца в 50 шлифах

по 300 зерен в каждом шлифе. В каждом шлифе оператор выбрал 10 участков,

каждый участок является полем зрения, в каждом поле зрения он выбрал

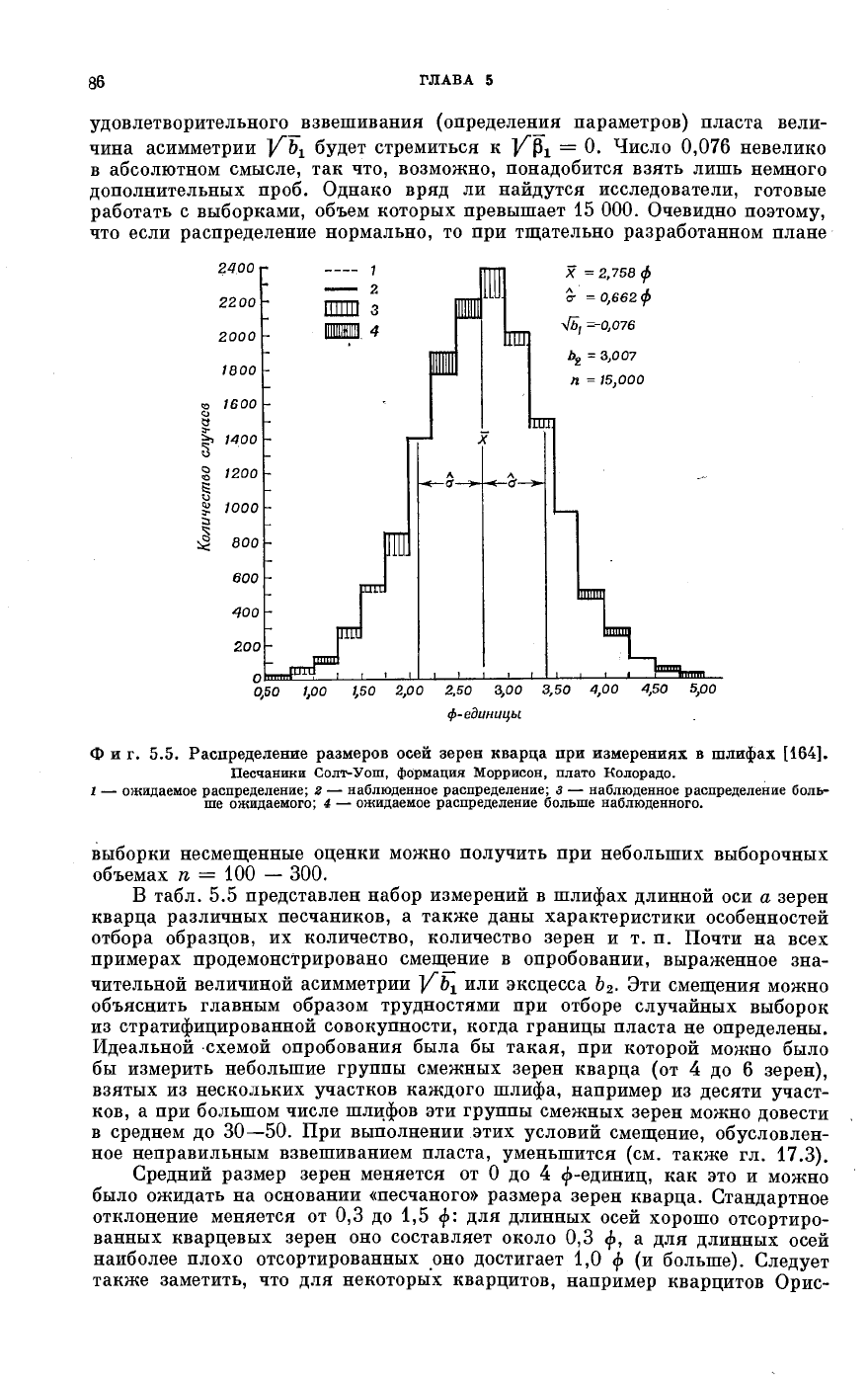
10 зерен. Результирующая гистограмма изображена на фиг. 5.5, а соответ-

ствующие статистики равны:

X = 2,758; σ = 0,662; 1/¾=—0,076;

= 3,007.

В результате проверки гипотез J^

= 0 и Yfi

= 3 оказалось, что

гипотеза Vfi

= 0 отвергается, a Vfi

— 3 принимается как не противоре-

чащая выборочным данным. Далее, допустив, что изучаемая генеральная

совокупность является ф-нормальной, можно рассчитать теоретическое

нормальное распределение с параметрами μ = 2,758 и σ = 0,662, затем

рассчитанную гистограмму наложить на наблюдаемую, как это сделано

на фиг. 5.5. где показана разница между наблюдаемым и ожидаемым рас-

пределениями. Больших расхождений здесь нет. Следовательно, нет и сис-

тематического смещения, а имеющиеся смещения, по-видимому, отражают

ошибки опробования и особенно часто — трудности, возникающие при

опробовании стратифицированной совокупности без адекватного определе-

ния границ слоя. Если мы примем, что изучаемая совокупность ф-нормаль-

на. то к соблюдению условий случайного опробования не будут предъявлены

какие-либо специфические требования, кроме рекомендации об увеличении

числа проб. Можно ожидать, что при увеличении числа проб по достижении

ГЛАВА 6

удовлетворительного взвешивания (определения параметров) пласта вели-

чина асимметрии Yb

будет стремиться к Yfi

= 0. Число 0,076 невелико

в абсолютном смысле, так что, возможно, понадобится взять лишь немного

дополнительных проб. Однако вряд ли найдутся исследователи, готовые

работать с выборками, объем которых превышает 15 ООО. Очевидно поэтому,

что если распределение нормально, то при тщательно разработанном плане

2400 г

2200

2000

1800

га 1600

|> 1400

§ 1200

э·

юоо

800

воо

400

ZOO

ПТТГП 3

L F

.Itl

X = 2,758 ф

σ = 0,662 ф

\[b, =-0,076

bg = 3,007

П = 15,000

шг

' ' ι u

шли

SO 1,00 1,50 2,00 2,50 3,00 3,5О 4,00 4,5О 5,00

ф-единицы

Фиг. 5.5. Распределение размеров осей зерен кварца при измерениях в шлифах [164].

Песчаники Солт-Уош, формация Моррисон, плато Колорадо.

I — ожидаемое распределение; г — наблюденное распределение; 3 — наблюденное распределение боль-

ше ожидаемого; 4 — ожидаемое распределение больше наблюденного.

выборки несмещенные оценки можно получить при небольших выборочных

объемах η = 100 - 300.

В табл. 5.5 представлен набор измерений в шлифах длинной оси а зерен

кварца различных песчаников, а также даны характеристики особенностей

отбора образцов, их количество, количество зерен и т. п. Почти на всех

примерах продемонстрировано смещение в опробовании, выраженное зна-

чительной величиной асимметрии Yb

или эксцесса Ь

. Эти смещения можно

объяснить главным образом трудностями при отборе случайных выборок

из стратифицированной совокупности, когда границы пласта не определены.

Идеальной схемой опробования была бы такая, при которой можно было

бы измерить небольшие группы смежных зерен кварца (от 4 до 6 зерен),

взятых из нескольких участков каждого шлифа, например из десяти участ-

ков, а при большом числе шлифов эти группы смежных зерен можно довести

в среднем до 30—50. При выполнении этих условий смещение, обусловлен-

ное неправильным взвешиванием пласта, уменьшится (см. также гл. 17.3).

Средний размер зерен меняется от 0 до 4 ф-единиц, как это и можно

было ожидать на основании «песчаного» размера зерен кварца. Стандартное

отклонение меняется от 0,3 до 1,5 ф: для длинных осей хорошо отсортиро-

ванных кварцевых зерен оно составляет около 0,3 ф, а для длинных осей

наиболее плохо отсортированных оно достигает 1,0 ф (и больше). Следует

также заметить, что для некоторых кварцитов, например кварцитов Орис-

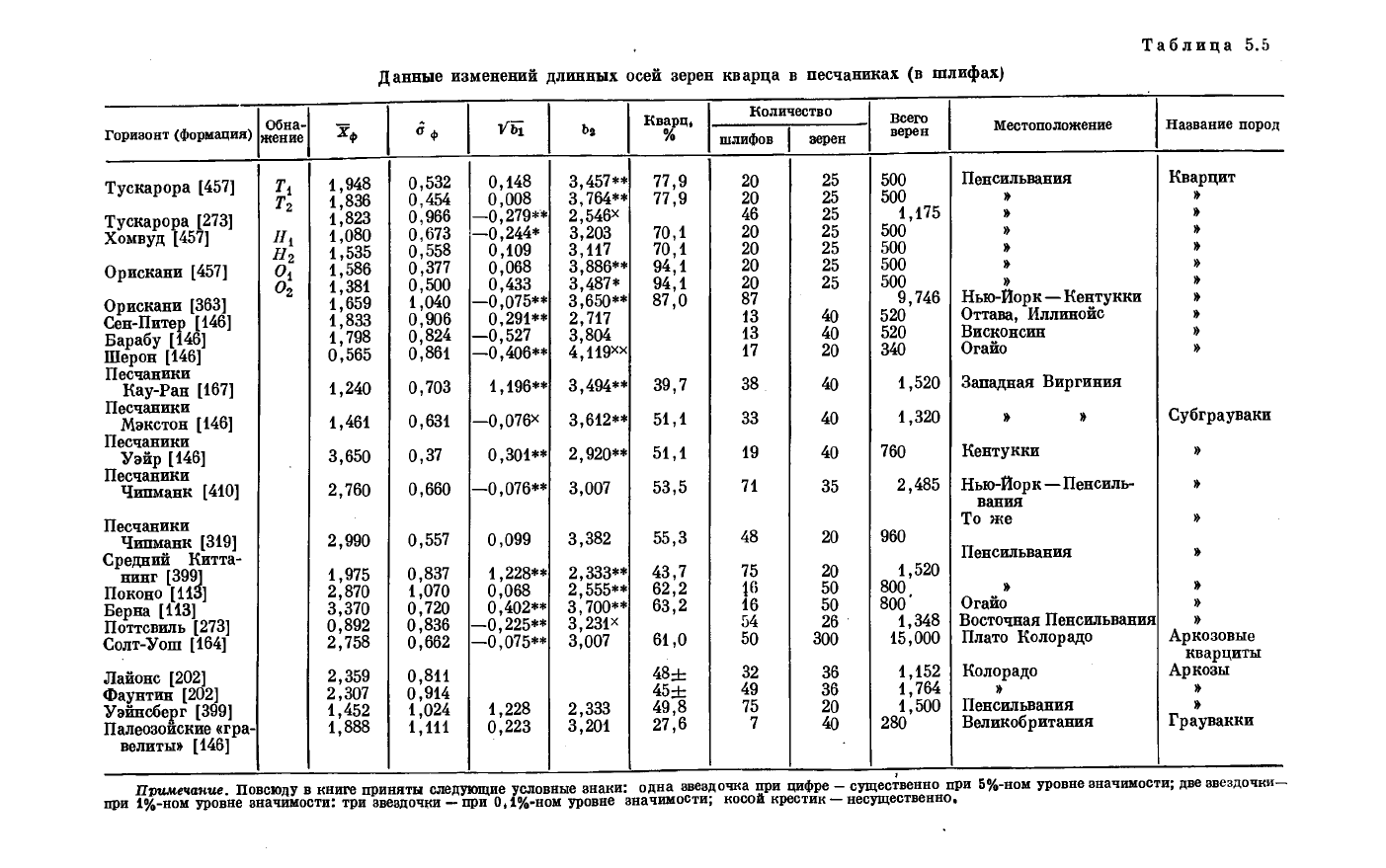
Таблица

5.5

Данные изменений длинных осей зерен кварца

песчаниках

(в

шлифах)

Обна-

жение

^bi

Ьа

Кварц,

Количество

всего

Местоположение

Название пород

Горизонт(формация)

Обна-

жение

Хф

^bi

Ьа

шлифов

зерен

верен

Местоположение

Название пород

Тускарора

[457]

Тускарора

[273]

Хомвуд

[457]

Орискани

[457]

Орискани

[363]

Сен-Питер

[146]

Барабу

[146]

Шерон

[146]

1,948

1,836

1,823

1,080

1,535

1,586

1,381

1,659

1,833

1,798

0,565

0,532

0,454

0,966

0,673

0,558

0,377

0,500

1,040

0,906

0,824

0,861

0,148

0,008

—0,279**

—0,244*

0,109

0,068

0,433

—0,075**

0,291**

—0,527

—0,406**

3,457**

3,764**

2,546

3,203

3,117

3,886**

3,487*

3,650**

2,717

3,804

4,119

хх

77,9

70,1

94,1

87,0

500

1,175

500

9,746

520

340

Пенсильвания

Нью-Йорк—Кентукки

Оттава, Иллинойс

Висконсин

Огайо

Кварцит

Песчаники

Кау-Ран

[167]

1,240

0,703

1,196** 3,494**

39,7

1,520

Западная Виргиния

Песчаники

Мэкстон

[146]

Песчаники

Уэйр

[146]

1,461

3,650

0,631

0,37

—0,076

0,301**

3,612**

2,920**

51,1

1,320

760

» »

Кентукки

Субграуваки

Песчаники

Чипманк

[410]

2,760

0,660

—0,076**

3,007

53,5

2,485

Нью-Йорк—Пенсиль-

вания

Песчаники

Чипманк

[319]

Средний Китта-

нинг

[399]

Поконо

[ИЗ]

Берна

[ИЗ]

Поттсвиль

[273]

Солт-Уош

[164]

Лайонс

[202]

Фаунтин

[202]

Уэйнсберг

[399]

Палеозойские «гра-

велиты»

[146]

2,990

1,975

2,870

3,370

0,892

2,758

2,359

2,307

1,452

1,888

0,557

0,837

1,070

0,720

0,836

0,662

0,811

0,914

1,024

1,111

0,099

1,228**

0,068

0,402**

—0,225**

—0,075**

1,228

0,223

3,382

2,333**

2,555**

3,700**

3,231

3,007

2,333

3,201

55,3

43.7

62,2

63,2

61,0

48±

45±

49.8

27,6

Ifi

300

960

1,520

800

800'

1,348

15,000

1,152

1,764

1,500

280

То же

Пенсильвания

Огайо

Восточная Пенсильвания

Плато Колорадо

Колорадо

Пенсильвания

Великобритания

Аркозовые

кварциты

Аркозы

Граувакки

Примечание. Повсюду

книге приняты следующие условные знаки: одна звездочка

при

цифре

существенно

при

5%-ном уровне значимости;

две

звездочки-

при

1%-ном уровне значимости:

три

звездочки

- при

0,1%-ном уровне значимости; косой крестик

—

несущественно.

ГЛАВА 6

кани, стандартное отклонение колеблется от 0,3 до 0,8 ф-единиц, т. е. эти

кварциты довольно хорошо отсортированы, в то время как вся формация

в целом отличается плохой сортировкой (σ = 1,0 ф-единиц). Последнее

качество свойственно кварцевым зернам большинства формаций. Таким

образом, диапазон изменений размеров кварцевых зерен можно оценить

как три стандартных отклонения вправо и влево от среднего значения либо

от 0 до 6 ф-единиц относительно среднего, равного 3 ф. Схема опробова-

ния, необходимая для оценки стандартного отклонения в установленных

доверительных пределах, рассчитана в гл. 17.3 с использованием диапазона

от 0,3 до 1,5 ф-единиц.

Характерно, что в большинстве случаев при косвенных способах изме-

ренное среднее значение связано некоторым отношением с дисперсией ([151,

212] и гл. 15), а при измерениях длинных осей зерен кварца в шлифах эти

величины независимы [167]. В случайных выборках из нормальной сово-

купности среднее значение независимо от дисперсии и стандартного откло-

нения. Это условие необходимо выполнять при отборе проб, если для харак-

теристики размеров зерен породы нужно получить обе основные оценки.

5.8. РАСПРЕДЕЛЕНИЕ РАЗМЕТОВ ПРИ ПРЯМЫХ ИЗМЕРЕНИЯХ

Прямой способ измерения зерен чрезвычайно заманчив. Определяя

размеры осей отдельных свободных зерен кварца, мы получаем меру, непо-

средственно относящуюся к понятию размера P = / (s, sh). Как упомина-

лось выше, информация, получаемая в результате этих измерений, достигает

так называемого уровня шкалы отношений. Кроме того, вполне вероятно,

что переменная находится здесь в прямом отношении к скорости потока,

как 1 : 1 (гл. 13), так что этот способ обеспечивает интерпретацию относи-

тельно энергии происходивших процессов, являясь тем самым мощным

средством петрологических исследований. Одна из положительных сторон

этого способа состоит в том, что он дает возможность измерять частицы

любых размеров — от пылеватых до крупных глыб. Занимаясь изучением

частиц кварцевого состава, имеющих самый разный размер, мы знакомимся

с максимальным диапазоном изменений размеров и других частиц.

Пай [338] был одним из первых исследователей, рекомендовавших этот

способ. Многие исследователи анализировали этим способом галечниковые

отложения (для справок см. работу [329, стр. 51—54]). Хале [203] разрабо-

тал альтернативный способ, позволяющий одновременно измерять харак-

теристики формы и размера, обеспечив тем самым оценку P = / (s, sh)

путем «чистого измерения». Таким образом, этот способ дает возможность

отделить изменчивость размера от изменчивости формы с помощью матема-

тического анализа [181]. Измерение совместной изменчивости в размере

и форме обеспечивает получение очень ценных данных, отражающих малей-

шие изменения и пригодных для детальных реконструкций условий осадко-

накопления [28, 204, 295].

При этом способе объем выборки η определяется непосредственно,

и здесь можно применить понятие числа степеней свободы; статистические

оценки, получаемые на основе метода моментов, можно использовать для

проверки гипотез. Для выяснения распределения генеральной совокуп-

ности здесь используется логнормальная, или ф-нормальная, модель. При

условии детального изучения размеров осей зерен кварца и тщательно

обдуманного и проведенного опробования эта модель дает возможность

получить распределение, лишь незначительно отличающееся от нормаль-

ного, получаемого в результате случайного опробования [163, 167, 169,

170, 176].

Было обнаружено, что если генеральная совокупность полностью доступ-

на, как, например, хорошо обнаженная стенка шурфа [170] или расчистка

ПРЕДСТАВЛЕНИЕ РЕЗУЛЬТАТОВ ИЗМЕРЕНИЙ

делювия [169], и бороздовые пробы отбираются по всей доступной (в данном

случае существующей) совокупности, то получаемые статистические оценки

существенно не отличаются от ожидаемых для случайной выборки из нор-

мальной совокупности. Если берутся стратифицированные случайны»

выборки, число наблюдений в выборке и число опробуемых слоев являются

определяющими для получения несмещенных оценок. Как и следовало

ожидать, при умело сбалансированном опробовании оценки приближаются

к оценкам из нормальной совокупности. При точечном опробовании страти-

фицированных пород некоторые слои попадают в выборку дважды, другие,

наоборот, совершенно выпадают из сферы опробования. Получаемые здесь

оценки довольно далеки от несмещенных (см., например, работы [169, 170,

411, 412]). При изучении шлифов процедура выбора зерен близка к точеч-

ному опробованию, чем и объясняется значительная асимметрия и эксцес-

сивность распределения. Было обнаружено, что если выборка относится

к одной и той же гомогенной генеральной совокупности, например к слою

или единице седиментации, она должна состоять из 30—50 элементов, всего

же нужно опробовать 16—20 слоев. Такая схема отбора представляется

наиболее оптимальной [169, 170, 176, 411, 412]. Многочисленные испытания

модели опробования, показанные на фиг. 2.3, свидетельствуют о том, что

для достижения несмещенных оценок по случайным выборкам нужны очень

тщательно сбалансированные схемы опробования и что даже небольшие

отклонения вносят значительное смещение. Поэтому, чтобы добиться слу-

чайного опробования логнормальной, или ф-нормальной, совокупности,

необходим точный контроль всей программы опробования. Наиболее просто

контроль можно осуществить с помощью непоередственного измерения

отдельных элементов (зерен или галек). Hn путем измерений в шлифах,

ни косвенными способами (метод пипетки или просеивания) такого контроля

осуществить нельзя без помощи очень сложных специальных исследований.

При измерении в шлифах хорошо сбалансированную программу опробования

очень трудно составить без предварительных специальных исследований.

В случае косвенных способов пробы точечного опробования составляют

20 г или от 100 до 150 г, в то время как для получения оценок, близких

к несмещенным, требуется значительно больший объем выборок.

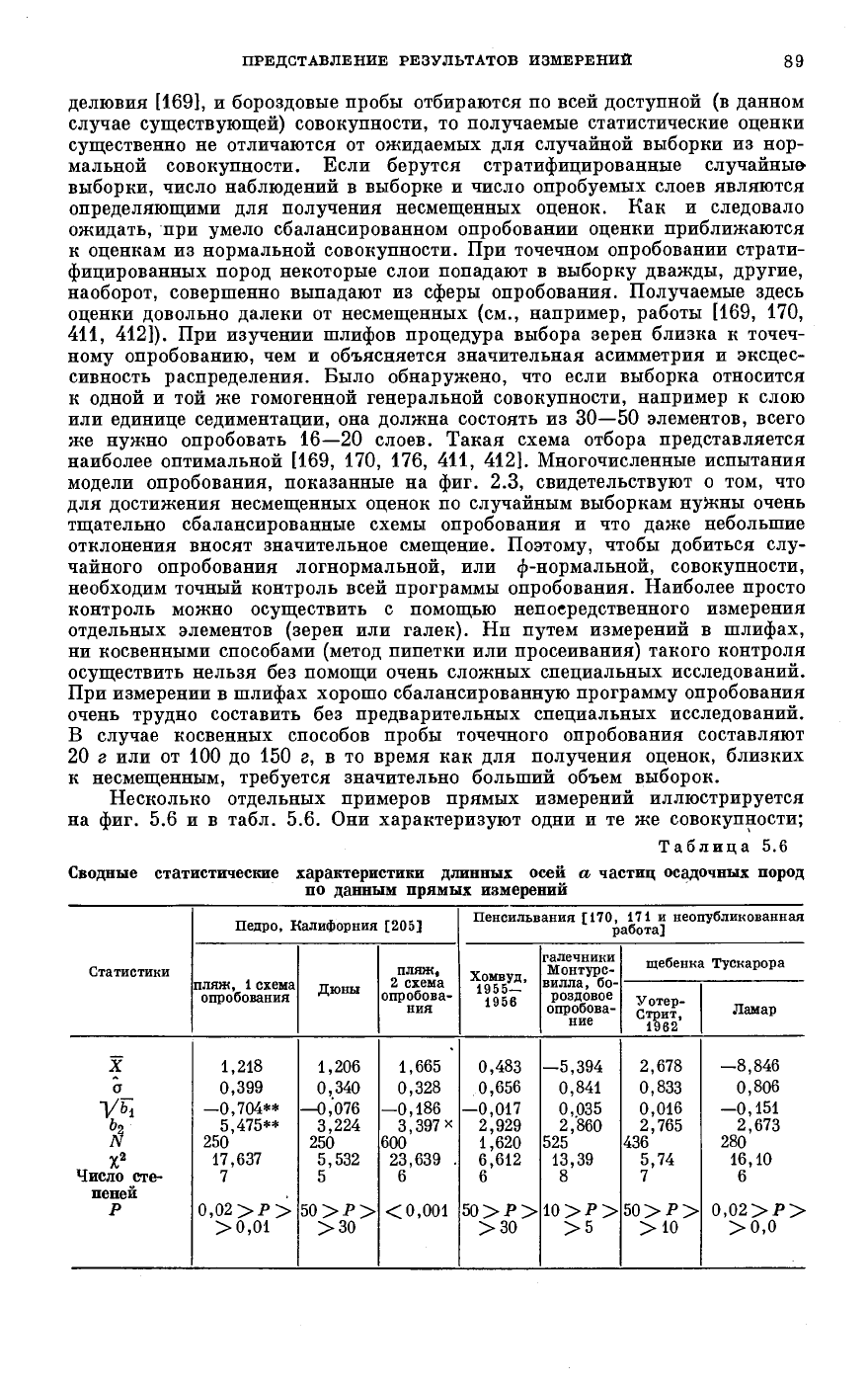
Несколько отдельных примеров прямых измерений иллюстрируется

на фиг. 5.6 и в табл. 5.6. Они характеризуют одни и те же совокупности;

Таблица 5.6

Сводные статистические характеристики длинных oceS а частиц осадочных пород

по данным прямых измерений

Педро, Калифорния [205]

Пенсильвания [170, 171 и неопубликованная

работа]

Статистики

пляж, 1 схема

опробования

пляж,

2 схема

опробова-

ния

Хомвуд,

галечники

Монтурс-

вилла, бо-

роздовое

опробова-

ние

щебенка Тускарора

пляж, 1 схема

опробования

Дюны

пляж,

2 схема

опробова-

ния

1955—·

1956

галечники

Монтурс-

вилла, бо-

роздовое

опробова-

ние

Уотер-

Стрит,

1962

Ламар

1,218

1,206 1,665

0,483

—5,394

2,678

—8,846

0,399

0,340

0,328 0,656

0,841 0,833

0,806

Число сте-

—0,704**

5,475**

250

17,637

—0,076

3,224

250

5,532

—0,186

3,397х

600

23,639 .

-0,017

2,929

1,620

6,612

0,035

2/860

525

13,39

0,016

2,765

436

5,74

-0,151

2,673

280

16,10

пеней

P 0,02>i>>

>0,01

50 >

-P

>30

<0,001

> P >

>30

10>Р>

50>Р>

>10

0,02 > P >

>0,0

ГЛАВА 6

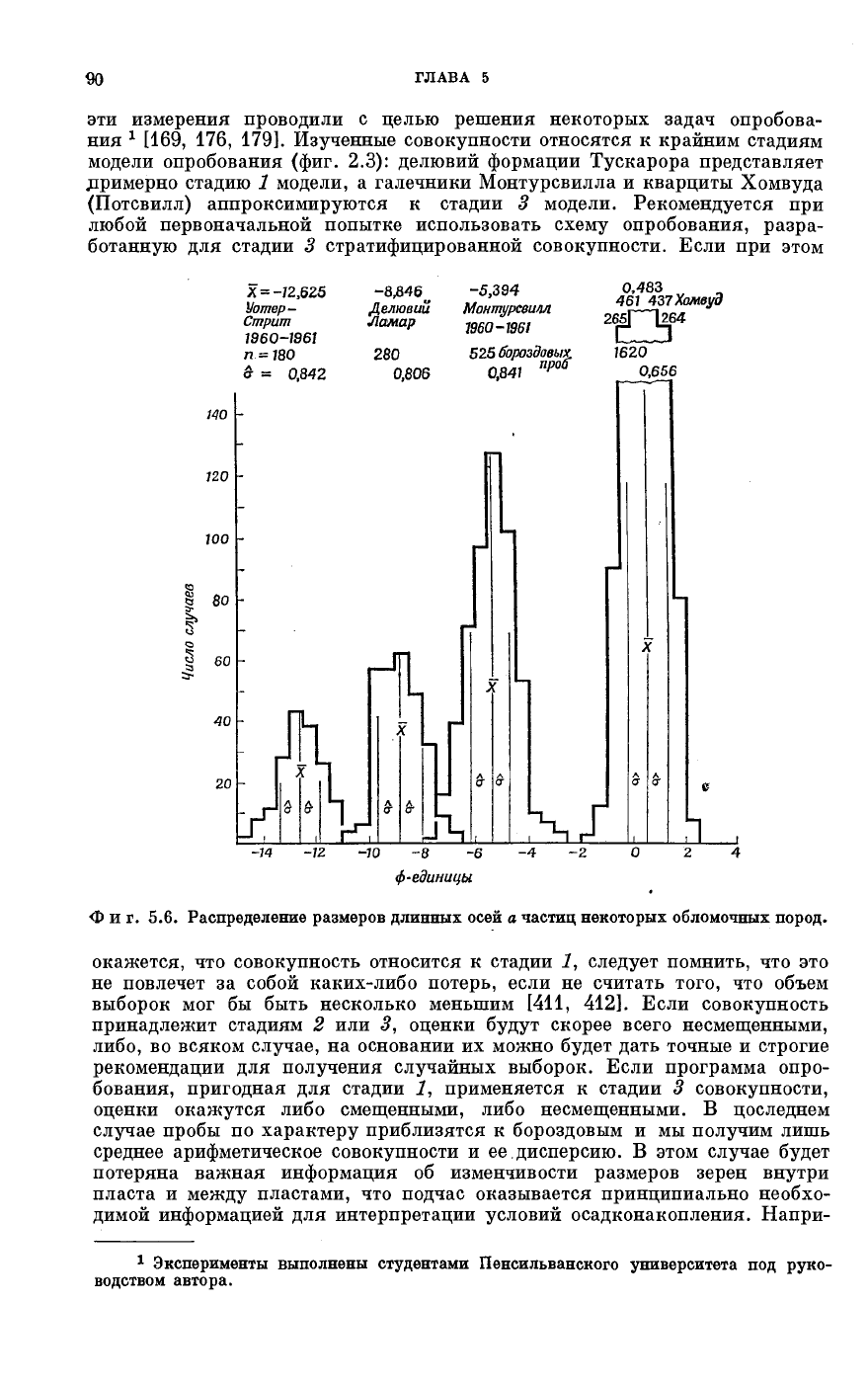
эти измерения проводили с целью решения некоторых задач опробова-

ния

[169, 176, 179]. Изученные совокупности относятся к крайним стадиям

модели опробования (фиг. 2.3): делювий формации Тускарора представляет

.примерно стадию 1 модели, а галечники Монтурсвилла и кварциты Хомвуда

(Потсвилл) аппроксимируются к стадии 3 модели. Рекомендуется при

любой первоначальной попытке использовать схему опробования, разра-

ботанную для стадии 3 стратифицированной совокупности. Если при этом

X = -/2,625

Уотер -

Стрит

1960-1961

η = 180

σ = 0,842

140 -

IZO

100

I 80

-8,846^

Делювий

Ламар

280

0,806

-5,394

Монтурсвила

1960-1961

525

бороздовых.

0,841

np0i

0,483

461 437Хомвуд

26QS4

1620

0,656

-14 -IZ -JO -8 -6 -4

ф-единицы.

Фиг. 5.6. Распределение размеров длинных осей а частиц некоторых обломочных пород.

окажется, что совокупность относится к стадии 1, следует помнить, что это

не повлечет за собой каких-либо потерь, если не считать того, что объем

выборок мог бы быть несколько меньшим [411, 412]. Если совокупность

принадлежит стадиям 2 или 3, оценки будут скорее всего несмещенными,

либо, во всяком случае, на основании их можно будет дать точные и строгие

рекомендации для получения случайных выборок. Если программа опро-

бования, пригодная для стадии 1, применяется к стадии 3 совокупности,

оценки окажутся либо смещенными, либо несмещенными. В цоследнем

случае пробы по характеру приблизятся к бороздовым и мы получим лишь

среднее арифметическое совокупности и ее дисперсию. В этом случае будет

потеряна важная информация об изменчивости размеров зерен внутри

пласта и между пластами, что подчас оказывается принципиально необхо-

димой информацией для интерпретации условий осадконакопления. Напри-

Эксперименты выполнены студентами Пенсильванского университета под руко-

водством автора.

ПРЕДСТАВЛЕНИЕ РЕЗУЛЬТАТОВ ИЗМЕРЕНИЙ

мер, диапазон изменений размеров кварцевых зерен ледниковых наносов

и морских пляжей вполне может быть одинаковым и даже средние значе-

ния могут быть близкими, тем не менее морена плохо стратифицирована,

т. е. приближается к стадии 1, в то время как пески морских пляжей будут

почти наверняка относиться к стадии 3 [411, 412]. Следовательно, особен-

ности изменчивости внутри выборки и между выборками имеют решающее

значение в определении степени селективной сортировки и как следствие —

в установлении условий осадконакопления.

В табл. 5.6 приведено слишком мало выборок, чтобы можно было гово-

рить о диапазоне средних значений, который находится в широких преде-

лах — от 1 ф-единицы (500 мк) до 13 ф-единиц. В то же время породы, све-

денные в таблице, представляют разную степень сортировки со стандартным

отклонением от 0,3 до 0,84 ф-единиц. Как и следовало ожидать, наиболее

хорошо отсортированными породами являются пляжные и дюнные пески

со стандартным отклонением около 0,3 φ (сравните с данными сортиров-

ки, полученными путем измерения длинных осей зерен кварца в шлифах).

Для делювия можно было ожидать широкого диапазона изменений разме-

ров, и действительно, стандартное отклонение достигает здесь около 0,8 ф.

Размах величины изменений длинных осей галек кварцитов из галечников

Монтурсвилла приближается к величине булыжников из делювия. Различия

между этими отложениями лежат в степени сортировки внутри проб и между

пробами, причем делювий напоминает стадию 7, а галечники приближаются

к стадии 3.

На примере двух серий исследований длинных осей зерен кварца пляжа

в Педро, графство Сан-Матео (Калифорния) [204], иллюстрируется эффект

различных схем опробования. Согласно схеме 1, было отобрано 5 точечных

проб по 50 зерен в каждой, а по схеме 2, представляющей попытку страти-

фицированного случайного опробования,— по 6 зерен, взятых из проб,

состоящих из 20—50 зерен, отобранных по сетке в 100 точках. Сетка была

построена пятью вертикальными линиями, расположенными на расстоянии

двух дюймов одна от другой, и 20 горизонтальными, проведенными через

полдюйма. Среднее значение и стандартное отклонение по 600 зернам (схе-

ма 2) сходны с соответствующими статистиками, полученными по 250 зернам

(схема 1). Однако показатели асимметрии и эксцесса по схеме 2 значительно

меньше, чем по схеме 1, что служит указанием на то, что, если стратифициро-

ванное опробование достигает условий случайной выборки, оно приносит

несмещенные статистики. Если проверить гипотезу о нормальности с помо-

щью х

-критерия, никакой из рассматриваемых анализов не приведет к нор-

мальному распределению; отклонения по схеме 1 встречаются как в центре,

так и по краям распределения. Основные отклонения по схеме 2 заключены

в двух центральных классах. Единственная рекомендация, которую можно

дать с целью улучшения схемы 1,— это увеличить как число проб, так

и их размер. С другой стороны, ожидаемая ф-нормальная модель схемы 2

требует большего количества измерений в центральной части распределения.

5.9. ИСПОЛЬЗОВАНИЕ РЕЗУЛЬТАТОВ АНАЛИЗА РАСПРЕДЕЛЕНИЯ

РАЗМЕРОВ ЗЕРЕН

Судя по опубликованным данным, имеется широкая область применения

результатов определений размеров (для справок см. [329, стр. 54]). Работы

по определению размеров начаты довольно давно и на них затрачиваются

значительные средства. В результате этих работ получено много различных

данных, но все они остаются в основном чисто эмпирическими качественными

данными, не обеспечивающими однозначной петрологической интерпретации.

Некоторые причины такого неудовлетворительного положения уже рас-

сматривались. Обычно уровень получаемой информации оказывается недо-