Gregersen E. (editor) The Britannica Guide to Statistics and Probability
Подождите немного. Документ загружается.

7 The Britannica Guide to Statistics and Probability 7
200
n bodies, have led to the discipline of topology, which
occupies the centre of the stage of mathematics. Many
combinatorial problems were posed during the 19th cen-
tury as purely recreational problems and are identified
by such names as “the problem of eight queens” and “the
Kirkman school girl problem.” Conversely, the study of
triple systems begun by Thomas P. Kirkman in 1847 and
pursued by Swiss-born German mathematician Jakob
Steiner in the 1850s was the beginning of the theory of
design. Among the earliest books devoted exclusively to
combinatorics are the German mathematician Eugen
Netto’s Lehrbuch der Combinatorik (1901; “Textbook of
Combinatorics”) and the British mathematician Percy
Alexander MacMahon’s Combinatory Analysis (1915–16),
which provide a view of combinatorial theory as it
existed before 1920.
Combinatorics During the 20th Century
Many factors have contributed to the quickening pace
of development of combinatorial theory since 1920.
One of these was the development of the statistical the-
ory of the design of experiments by the English
statisticians Ronald Fisher and Frank Yates, which has
given rise to many problems of combinatorial interest.
The methods initially developed to solve them have
found applications in such fields as coding theory.
Information theory, which arose around midcentury,
has also become a rich source of combinatorial prob-
lems of a quite new type.
Another source of the revival of interest in combina-
torics is graph theory, the importance of which lies in the
fact that graphs can serve as abstract models for many dif-
ferent kinds of schemes of relations among sets of objects.
201
7
Combinatorics 7
Its applications extend to operations research, chemistry,
statistical mechanics, theoretical physics, and socioeco-
nomic problems. The theory of transportation networks
can be regarded as a chapter of the theory of directed
graphs. One of the most challenging theoretical problems,
the four-colour problem belongs to the domain of graph
theory. It has also applications to such other branches of
mathematics as group theory.
The development of computer technology in the sec-
ond half of the 20th century is a main cause of the interest
in finite mathematics in general and combinatorial theory
in particular. Combinatorial problems arise in numerical
analysis as well as in the design of computer systems and
the application of computers to such problems as those of
information storage and retrieval.
Statistical mechanics is one of the oldest and most
productive sources of combinatorial problems. Much
important combinatorial work has been done by applied
mathematicians and physicists since the mid-20th cen-
tury, such as the work on Ising models.
In pure mathematics, combinatorial methods have
been used with advantage in such diverse fields as proba-
bility, algebra (finite groups and fields, matrix and lattice
theory), number theory (difference sets), set theory
(Sperner’s theorem), and mathematical logic (Ramsey’s
theorem).
In contrast to the wide range of combinatorial prob-
lems and the multiplicity of methods that have been
devised to deal with them stands the lack of a central
unifying theory. Unifying principles and cross connec-
tions, however, have begun to appear in various areas
of combinatorial theory. The search for an underlying
pattern that may indicate in some way how the diverse
parts of combinatorics are interwoven is a challenge
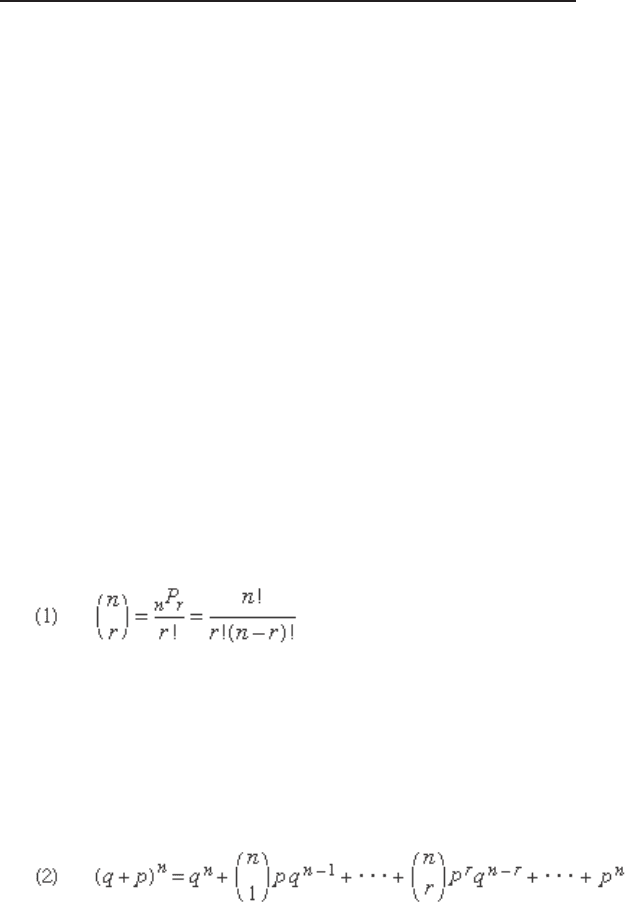
7 The Britannica Guide to Statistics and Probability 7
202
that faces mathematicians in the first quarter of the
21st century.
pRobleMs of enuMeRaTion
Permutations and Combinations
Binomial Coefficients
An ordered set a
1
, a
2
, . . . , a
r
of r distinct objects selected
from a set of n objects is called a permutation of n things
taken r at a time. The number of permutations is given by
n
P
n
= n ( n − 1)( n - 2) · · · ( n − r + 1). When r = n , the number
n
P
r
=
n ( n − 1)( n − 2) · · · is simply the number of ways of arranging
n distinct things in a row. This expression is called factorial
n and is denoted by n !. It follows that
n
P
r
= n !/( n − r )!. By
convention 0! = 1.
A set of r objects selected from a set of n objects with-
out regard to order is called a combination of n things
taken r at a time. Because each combination gives rise to r !
permutations, the number of combinations, which is writ-
ten (
n
/
r
), can be expressed in terms of factorials
.
The number (
n
/
r
) is called a binomial coeffi cient
because it occurs as the coeffi cient of p
r
q
n
-
r
in the bino-
mial expansion—that is, the re-expression of ( q + p )
n
in a
linear combination of products of p and q
.

203
7
Combinatorics 7
in the binomial expansion is the probability that an event
the chance of occurrence of which is p occurs exactly r
times in n independent trials.
The answer to many different kinds of enumeration
problems can be expressed in terms of binomial coeffi -
cients. The number of distinct solutions of the equation x
1
+ x
2
+ · · · + x
n
= m , for example, in which m is a non-negative
integer m ≥ n and in which only non-negative integral val-
ues of x
i
are allowed is expressible this way, as was found
by the 17th- and 18th-century French-born British mathe-
matician Abraham De Moivre
.
Multinomial Coefficients
If S is a set of n objects, and n
1
, n
2
, · · · , n
k
are non-negative
integers satisfying n
1
+ n
2
+ · · · + n
k
= n , then the number of
ways in which the objects can be distributed into k boxes,
X
1
, X
2
, · · · , X
k
, such that the box X
i
contains exactly n
i
objects is given in terms of a ratio constructed of
factorials
.
This number, called a multinomial coeffi cient, is the
coeffi cient in the multinomial expansion of the n th power
of the sum of the { p
i
}
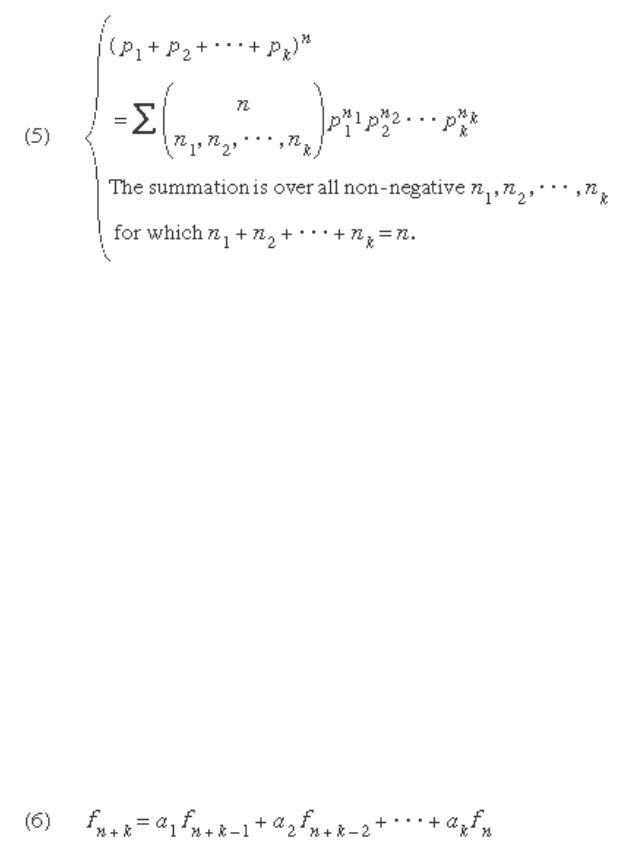
7 The Britannica Guide to Statistics and Probability 7
204
If all the { p
i
} are non-negative and sum to 1 and if
there are k possible outcomes in a trial in which the
chance of the i th outcome is p
i
, then the i th summand in
the multinomial expansion is the probability that in n
independent trials the i th outcome will occur exactly n
i
times, for each i , 1 ≤ 1 ≤ k .
Recurrence Relations and
Generating Functions
If f
n
is a function defi ned on the positive integers, then a
relation that expresses f
n + k
as a linear combination of func-
tion values of integer index less than n + k , in which a fi xed
constant in the linear combination is written a
i
, is called a
recurrence relation
.
The relation together with the initial values f
0
, f
1
, · · · ,
f
k -1
determines f
n
for all n . The function F ( x ) constructed of
a sum of products of the type f
n
x
n
, the convergence of
which is assumed in the neighbourhood of the origin, is
called the generating function of f
n
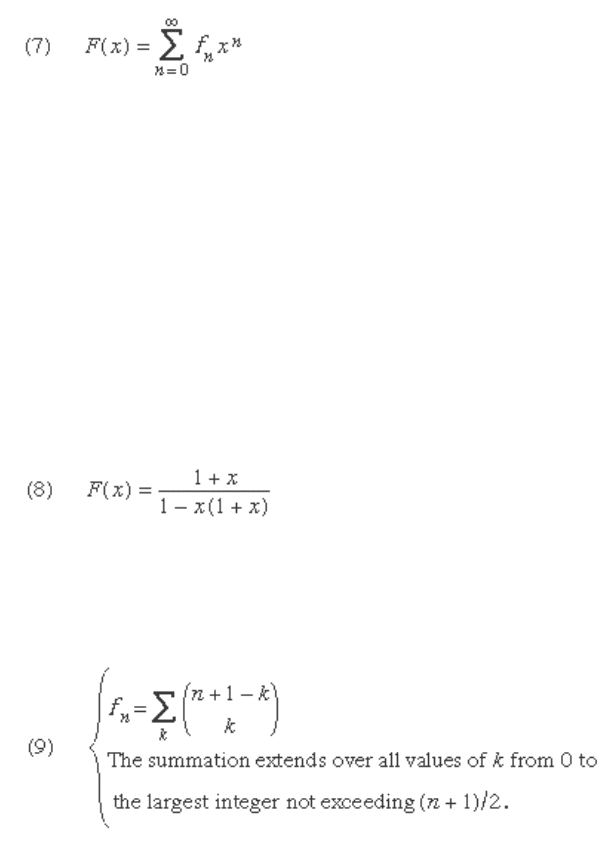
205
7
Combinatorics 7
.
The set of the fi rst n positive integers will be written
X
n
. It is possible to fi nd the number of subsets of X
n
con-
taining no two consecutive integers, with the convention
that the null set counts as one set. The required number
will be written f
n
. A subset of the required type is either a
subset of X
n
-1
or is obtained by adjoining n to a subset of
X
n
-2
. Therefore f
n
is determined by the recurrence rela-
tion f
n
= f
n
-1
+ f
n
-2
with the initial values f
0
= 1, f
1
= 2. Thus f
2
= 3, f
3
= 5, f
4
= 8, and so on. The generating function F ( x ) of
f
n
can be calculated
,
and from this a formula for the desired function f
n
can be
obtained
That f
n
= f
n -1
+ f
n -2
can now be directly checked.
Partitions
A partition of a positive integer n is a representation of n
as a sum of positive integers n = x
1
+ x
2
+ · · · + x
k
, x
i
≥ 1, i = 1,
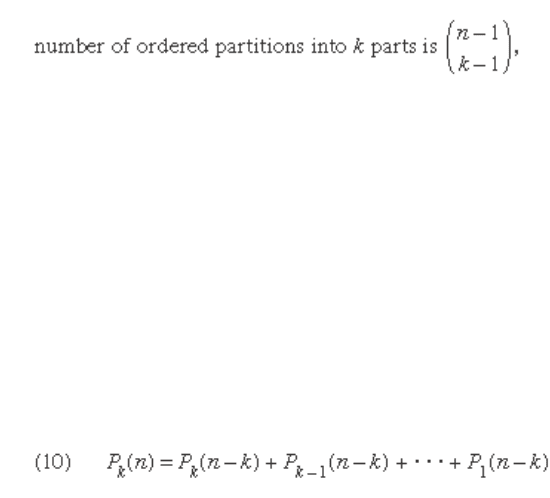
7 The Britannica Guide to Statistics and Probability 7
206
2, · · · , k . The numbers x
i
are called the parts of the parti-
tion. The
for this is the number of ways of putting k − 1 separating
marks in the n − 1 spaces between n dots in a row. The the-
ory of unordered partitions is much more diffi cult and has
many interesting features. An unordered partition can be
standardized by listing the parts in a decreasing order.
Thus n = x
1
+ x
2
+ · · · + x
k
, x
1
≥ x
2
≥ · · · ≥ x
k
≥ 1. In what follows
partition will mean an unordered partition.
The number of partitions of n into k parts will be
denoted by P
k
( n ), and a recurrence formula for it can be
obtained from the defi nition
.
This recurrence formula, together with the initial con-
ditions P
k
( n ) = 0 if n < k , and P
k
( k ) = 1 determines P
k
( n ). It can
be shown that P
k
( n ) depends on the value of n (mod k !), in
which the notation x =
¯
a (mod b ) means that x is any number
that, if divided by b , leaves the same remainder as a does.
For example, P
3
( n ) = n
2
+ c
n
, in which c
n
= 0, −1/12, −1/3, +1/4, −1/3,
or −1/12, according as n is congruent to 0, 1, 2, 3, 4, or 5 (mod
6). P ( n ), which is a sum over all values of k from 1 to n of P
k
( n ),
denotes the number of partitions of n into n or fewer parts.
The Ferrers Diagram
Many results on partitions can be obtained by the use of
Ferrers diagram. The diagram of a partition is obtained by

207
7
Combinatorics 7
putting down a row of squares equal in number to the larg-
est part, then immediately below it a row of squares equal
in number to the next part, and so on.
By rotating the Ferrers diagram of the partition about
the diagonal, it is possible to obtain from the partition n =
x
1
+ x
2
+ · · · + x
k
the conjugate partition n = x
1
* + x
2
* + · · · x
n
*,
in which x
i
* is the number of parts in the original partition
of cardinality i or more. Thus, for example, the conjugate of
the partition of 14 is 14 = 5 + 4 + 3 + 1 + 1. Hence, the follow-
ing result is obtained:
(F
1
) The number of partitions of n into k parts is
equal to the number of partitions of n with k as the
largest part.
By using the Ferrers diagram, one can attain many results on partitions.
Copyright Encyclopaedia Britannica; rendering for this edition by
Rosen Educational Services
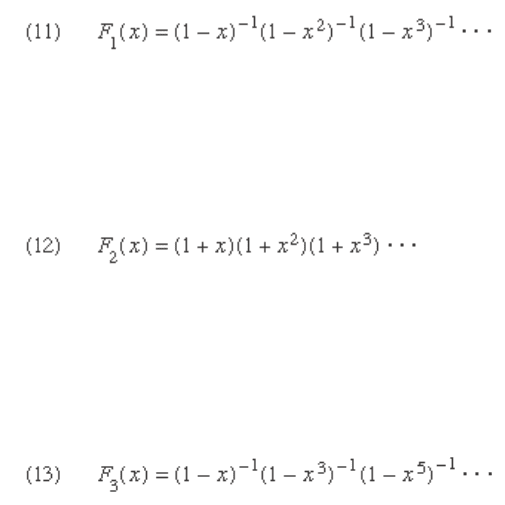
7 The Britannica Guide to Statistics and Probability 7
208
Other results obtainable by using Ferrer diagrams are:
(F
2
) The number of self-conjugate partitions of n
equals the number of partitions of n with all parts
unequal and odd.
(F
3
) the number of partitions of n into unequal
parts is equal to the number of partitions of n into
odd parts.
Generating functions can be used with advantage to study
partitions. For example, it can be proved that:
(G
1
) The generating function F
1
( x ) of P ( n ), the
number of partitions of the integer n , is a product
of reciprocals of terms of the type (1 - x
k
), for all
positive integers k , with the convention that
P (0)=1 :
(G
2
) The generating function F
2
( x ) of the number
of partitions of n into unequal parts is a product of
terms like (1 + x
k
), for all positive integers k :
(G
3
) The generating function F
3
( x ) of the number
of partitions of x consisting only of odd parts is a
product of reciprocals of terms of the type (1 - x
k
),
for all positive odd integers k :

209
7
Combinatorics 7
Thus to prove (F
3
) it is necessary only to show that the
generating functions described in (G
2
) and (G
3
) are equal.
This method was used by Euler.
The Principle of Inclusion and Exclusion:
Derangements
For a case in which there are N objects and n properties
A
1
, A
2
, · · · A
n
, the number N ( A
1
, A
2
), for example, will be
the number of objects that possess the properties A
1
, A
2
.
If N ( Ā
1
, Ā
2
, · · · , Ā
n
) is the number of objects possessing
none of the properties A
1
, A
2
, · · · , A
n
, then this number
can be computed as an alternating sum of sums involving
the numbers of objects that possess the properties
This is the principle of inclusion and exclusion
expressed by Sylvester.
The permutation of n elements that displaces each
object is called a derangement. The permutations them-
selves may be the objects and the property i may be the
property that a permutation does not displace the i th ele-
ment. In such a case N = n ! and N ( A
1
, A
2
) = ( n - 2)!, for
