Gregersen E. (editor) The Britannica Guide to Statistics and Probability

Подождите немного. Документ загружается.

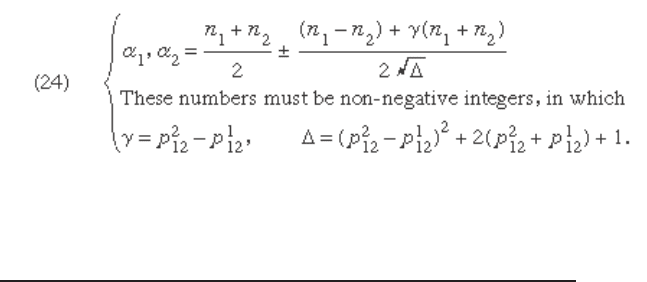
7 The Britannica Guide to Statistics and Probability 7

220

Sufﬁ cient conditions for the existence of association

schemes with given parameters are unknown, but for a

two-class association scheme W.S. Connor and the

American mathematician Willard H. Clatworthy in 1954

obtained some necessary conditions

laTin squaRes and

The packing pRobleM

Orthogonal Latin Squares

A Latin square of order k is deﬁ ned as a k × k square grid,

the k

cells of which are occupied by k distinct symbols of

a set X = 1, 2, . . . , k , such that each symbol occurs once in

each row and each column. Two Latin squares are said to

be orthogonal if, when superposed, any symbol of the ﬁ rst

square occurs exactly once with each symbol of the sec-

ond square.

A set of mutually orthogonal Latin squares is a set of

Latin squares any two of which are orthogonal. It is easily

shown that there cannot exist more than k − 1 mutually

orthogonal Latin squares of a given order k . When k − 1

mutually orthogonal Latin squares of order k exist, the set

is complete. A complete set always exists if k is the power

of a prime. An unsolved question is whether there can

exist a complete set of mutually orthogonal Latin squares

of order k if k is not a prime power.

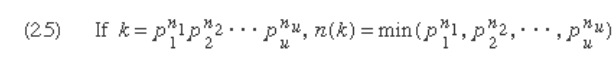
221

Combinatorics 7

Many types of experimental designs are based on Latin

squares. Hence, the construction of mutually orthogonal

Latin squares is an important combinatorial problem.

Letting the prime power decomposition of an integer k be

given, the arithmetic function n ( k ) is deﬁ ned by taking the

minimum of the factors in such a decomposition

Letting N ( k ) denote the maximum number of mutu-

ally orthogonal Latin squares of order k , the American

mathematician H.F. MacNeish in 1922 showed that there

always exist n ( k ) mutually orthogonal Latin squares of

order k and conjectured that this is the maximum num-

ber of such squares—that is, N ( k ) = n ( k ). There was also

the long-standing conjecture of Euler, formulated in

1782, that there cannot exist mutually orthogonal Latin

squares of order 4 t + 2, for any integer t . MacNeish’s con-

jecture, if true, would imply the truth of Euler’s but not

conversely. The American mathematician E.T. Parker in

1958 disproved the conjecture of MacNeish. This left

open the question of Euler’s conjecture. Bose and the

Indian mathematician S.S. Shrikhande in 1959–60

obtained the ﬁ rst counterexample to Euler’s conjecture

by obtaining two mutually orthogonal Latin squares of

order 22 and then generalized their method to disprove

Euler’s conjecture for an inﬁ nity of values of k = 2(mod

4). In 1959 Parker used the method of differences to

show the falsity of Euler’s conjecture for all k = (3 q + 1)/2,

in which q is a prime power, q =

3(mod 4). Finally, these

three mathematicians in 1960 showed that N ( k ) ≥ 2

whenever k > 6. It is pertinent to inquire about the

behaviour of N ( k ) for large k . The best result in this

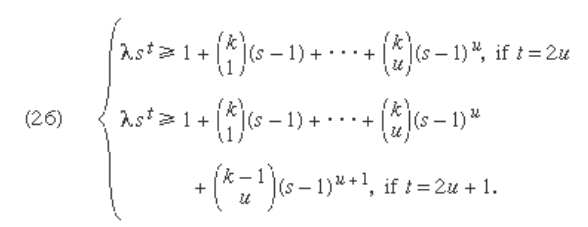
7 The Britannica Guide to Statistics and Probability 7

222

direction is due to R.M. Wilson in 1971. He shows that

N ( k ) ≥ k

1/17

− 2 for large k .

Orthogonal Arrays and the Packing Problem

A k × N matrix A with entries from a set X of s ≥ 2 symbols

is called an orthogonal array of strength t , size N , k con-

straints, and s levels if each t × N submatrix of A contains

all possible t × 1 column vectors with the same frequency

λ. The array may be denoted by ( N , k , s , t ). The number λ

is called the index of the array, and N = λ s

. This concept is

due to the Indian mathematician C.R. Rao and was

obtained in 1947.

Orthogonal arrays are a generalization of orthogonal

Latin squares. Indeed, the existence of an orthogonal

array of k constraints, s levels, strength 2, and index unity

is combinatorially equivalent to the existence of a set of

k − 2 mutually orthogonal Latin squares of order s . For a

given λ, s , and t it is an important combinatorial problem

to obtain an orthogonal array ( N , k , s , t ), N = s

, for which

the number of constraints k is maximal.

Orthogonal arrays play an important part in the the-

ory of factorial designs in which each treatment is a

combination of factors at different levels. For an orthogo-

nal array (λ s

, k , s , t ), t ≥ 2, the number of constraints k

satisﬁ es an inequality

223

Combinatorics 7

in which λs

is greater than or equal to a linear expression

in powers of (s − 1), with binomial coefﬁcients giving the

number of combinations of k − 1 or k things taken i at a

time (iu).

Letting GF(q) be a ﬁnite ﬁeld with q = p

elements, an

n × r matrix with elements from the ﬁeld is said to have

the property P

if any t rows are independent. The prob-

lem is to construct for any given r a matrix H with the

maximum number of rows possessing the property P

The maximal number of rows is denoted by n

(r, q). This

packing problem is of great importance in the theory of

factorial designs and also in communication theory,

because the existence of an n × r matrix with the property

leads to the construction of an orthogonal array (q

, n,

q, t) of index unity.

Again n × r matrices H with the property P

may be

used in the construction of error-correcting codes. A row

vector c′ is taken as a code word if and only if c′H = 0. The

code words then are of length n and differ in at least t + 1

places. If t = 2u, then u or fewer errors of transmission can

be corrected if such a code is used. If t = 2u + 1, an addi-

tional error can be detected.

A general solution of the packing problem is known

only for the case t = 2, the corresponding codes being the

one-error-correcting codes of the American mathemati-

cian Richard W. Hamming. When t = 3 the solution is

known for general r when q = 2 and for general q when r =

4. Thus, n

(r, 2) = (q

− 1)/(q − 1), n

(r, 2) = 2

r−1

, n

(3, q) = q + 1 or

q + 2, according as q is odd or even. If q > 2, then n

(4, q) = q

+ 1. The case q = 2 is especially important because in prac-

tice most codes use only two symbols, 0 or 1. Only fairly

large values of r are useful, say, r ≥ 25. The optimum value

of n

(r, 2) is not known. The BCH codes obtained by Bose

and Ray-Chaudhuri and independently by the French

direction is due to R.M. Wilson in 1971. He shows that

N(k) ≥ k

1/17

− 2 for large k.

Orthogonal Arrays and the Packing Problem

A k × N matrix A with entries from a set X of s ≥ 2 symbols

is called an orthogonal array of strength t, size N, k con-

straints, and s levels if each t × N submatrix of A contains

all possible t × 1 column vectors with the same frequency

λ. The array may be denoted by (N, k, s, t). The number λ

is called the index of the array, and N = λs

. This concept is

due to the Indian mathematician C.R. Rao and was

obtained in 1947.

Orthogonal arrays are a generalization of orthogonal

Latin squares. Indeed, the existence of an orthogonal

array of k constraints, s levels, strength 2, and index unity

is combinatorially equivalent to the existence of a set of

k − 2 mutually orthogonal Latin squares of order s. For a

given λ, s, and t it is an important combinatorial problem

to obtain an orthogonal array (N, k, s, t), N = s

, for which

the number of constraints k is maximal.

Orthogonal arrays play an important part in the the-

ory of factorial designs in which each treatment is a

combination of factors at different levels. For an orthogo-

nal array (λs

, k, s, t), t ≥ 2, the number of constraints k

satisﬁes an inequality

7 The Britannica Guide to Statistics and Probability 7

224

mathematician Alexis Hocquenghem in 1959 and 1960 are

based on a construction that yields an n × r matrix H with

the property P

in which r mu, n = 2

- 1, q = 2. They can

correct up to u errors.

gRaph TheoRy

Deﬁnitions

A graph G consists of a non-empty set of elements V(G)

and a subset E(G) of the set of unordered pairs of distinct

elements of V(G). The elements of V(G), called vertices of

G, may be represented by points. If (x, y) ∊ E(G), then the

edge (x, y) may be represented by an arc joining x and y.

Then x and y are said to be adjacent, and the edge (x, y) is

incident with x and y. If (x, y) is not an edge, then the ver-

tices x and y are said to be nonadjacent. G is a ﬁnite graph

if V(G) is ﬁnite. A graph H is a subgraph of G if V(H) ⊂

V(G) and E(H) ⊂ E(G).

A chain of a graph G is an alternating sequence of ver-

tices and edges x

, e

, x

, e

, · · · e

, x

, beginning and ending

with vertices in which each edge is incident with the two

vertices immediately preceding and following it. This

chain joins x

and x

and may also be denoted by x

, x

, · · · ,

, the edges being evident by context. The chain is closed

if x

= x

and open otherwise. If the chain is closed, it is

called a cycle, provided its vertices (other than x

and x

)

are distinct and n ≥ 3. The length of a chain is the number

of edges in it.

A graph G is labelled when the various υ vertices are

distinguished by such names as x

, x

, · · · x

. Two graphs G

and H are said to be isomorphic (written G ≃ H) if there

exists a one–one correspondence between their vertex

sets that preserves adjacency. Two isomorphic graphs

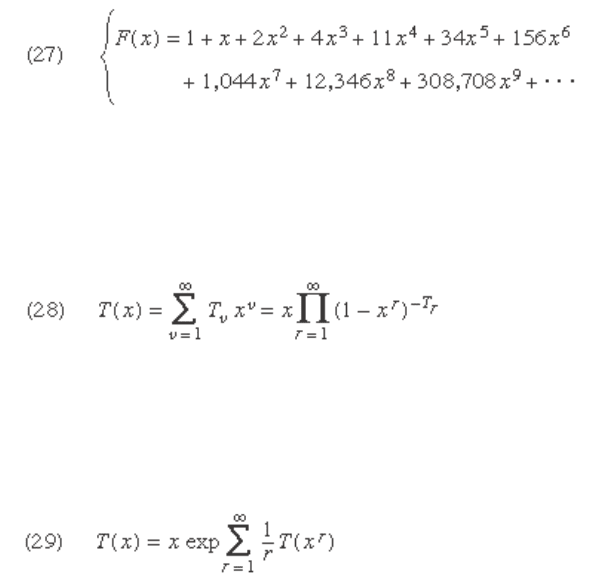
225

Combinatorics 7

count as the same (unlabelled) graph. A graph is said to be

a tree if it contains no cycle.

Enumeration of Graphs

The number of labelled graphs with υ vertices is 2

υ(υ − 1)/2

because υ(υ − 1)/2 is the number of pairs of vertices, and each

pair is either an edge or not an edge. Cayley in 1889 showed

that the number of labelled trees with υ vertices is υ

υ − 2

The number of unlabelled graphs with υ vertices can

be obtained by using Polya’s theorem. The ﬁ rst few terms

of the generating function F ( x ), in which the coefﬁ cient of

gives the number of (unlabelled) graphs with υ vertices,

can be given

A rooted tree has one point, its root, distinguished

from others. If T

is the number of rooted trees with υ ver-

tices, the generating function for T

can also be given

Polya in 1937 showed in his memoir already referred to

that the generating function for rooted trees satisﬁ es a

functional equation

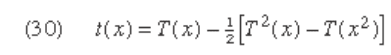
7 The Britannica Guide to Statistics and Probability 7

226

Letting t

be the number of (unlabelled) trees with υ

vertices, the generating function t ( x ) for t

can be obtained

in terms of T ( x )

This result was obtained in 1948 by the American

mathematician Richard R. Otter.

Many enumeration problems on graphs with speci-

ﬁ ed properties can be solved by the application of Polya’s

theorem and a generalization of it made by a Dutch math-

ematician, N.G. de Bruijn, in 1959.

Characterization Problems of Graph Theory

If there is a class C of graphs each of which possesses a

certain set of properties P , then the set of properties P is

said to characterize the class C , provided every graph G

possessing the properties P belongs to the class C .

Sometimes it happens that there are some exceptional

graphs that possess the properties P . Many such charac-

terizations are known. Consider a typical example.

A complete graph K

is a graph with m vertices, any two

of which are adjacent. The line graph H of a graph G is a

graph the vertices of which correspond to the edges of G ,

any two vertices of H being adjacent if and only if the corre-

sponding edges of G are incident with the same vertex of G .

A graph G is said to be regular of degree n

if each ver-

tex is adjacent to exactly n

other vertices. A regular graph

of degree n

with υ vertices is said to be strongly regular

with parameters (υ, n

, p

) if any two adjacent vertices

are both adjacent to exactly p

other vertices and any two

nonadjacent vertices are both adjacent to exactly p

other

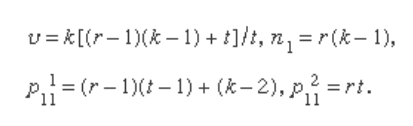
227

Combinatorics 7

vertices. A strongly regular graph and a two-class associa-

tion are isomorphic concepts. The treatments of the

scheme correspond to the vertices of the graph, two treat-

ments being either ﬁ rst associates or second associates

according as the corresponding vertices are either adja-

cent or nonadjacent.

It is easily proved that the line graph T

( m ) of a com-

plete graph K

, m ≥ 4 is strongly regular with parameters

υ = m ( m − 1)/2, n

= 2( m − 2), p

= m − 2, p

= 4.

It is surprising that these properties characterize T

( m )

except for m = 8, in which case there exist three other

strongly regular graphs with the same parameters noniso-

morphic to each other and to T

( m ).

A partial geometry ( r , k , t ) is a system of two kinds of

objects, points, and lines, with an incidence relation obey-

ing the following axioms:

1. Any two points are incident with not more

than one line.

2. Each point is incident with r lines.

3. Each line is incident with k points.

4. Given a point P not incident with a line l, there

are exactly t lines incident with P and also with

some point of l.

A graph G is obtained from a partial geometry by tak-

ing the points of the geometry as vertices of G , two vertices

of G being adjacent if and only if the corresponding points

are incident with the same line of the geometry. It is

strongly regular with parameters

7 The Britannica Guide to Statistics and Probability 7

228

The question of whether a strongly regular graph with

the previous parameters is the graph of some partial geom-

etry is of interest. It was shown by Bose in 1963 that the

answer is in the afﬁ rmative if a certain condition holds

Not much is known about the case if this condition is

not satisﬁ ed, except for certain values of r and t . For exam-

ple, T

( m ) is isomorphic with the graph of a partial

geometry (2, m − 1, 2). Hence, for m > 8 its characterization

is a consequence of the above theorem. Another conse-

quence is the following:

Given a set of k -1- d mutually orthogonal Latin squares

of order k , the set can be extended to a complete set of k -1

mutually orthogonal squares if a condition holds

The case d = 2 is due to Shrikhande in 1961 and the gen-

eral result to the American mathematician Richard H.

Bruck in 1963.

applicaTions of gRaph TheoRy

Planar Graphs

A graph G is said to be planar if it can be represented on a

plane in such a fashion that the vertices are all distinct

points, the edges are simple curves, and no two edges meet

one another except at their terminals. Two graphs are said

to be homeomorphic if both can be obtained from the

same graph by subdivisions of edges.

229

Combinatorics 7

The Km

n graph is a graph for which the vertex set can

be divided into two subsets, one with m vertices and the

other with n vertices. Any two vertices of the same sub-

set are nonadjacent, whereas any two vertices of different

subsets are adjacent. The Polish mathematician Kazimierz

Kuratowski in 1930 proved the following famous theorem:

A necessary and sufﬁcient condition for a graph G to be pla-

nar is that it does not contain a subgraph homeomorphic to

either K

or K

3,3

An elementary contraction of a graph G is a transforma-

tion of G to a new graph G

, such that two adjacent vertices

u and υ of G are replaced by a new vertex w in G

and w is

adjacent in G

to all vertices to which either u or υ is adjacent

in G. A graph G* is said to be a contraction of G if G* can be

obtained from G by a sequence of elementary contractions.

The following is another characterization of a planar

graph due to the German mathematician K. Wagner in

1937. A graph is planar if and only if it is not contractible to

or K

3,3

The Four-Colour Map Problem

For more than a century the solution of the four-colour

map problem eluded every analyst who attempted it. The

problem may have attracted the attention of Möbius, but

the ﬁrst written reference to it seems to be a letter from

one Francis Guthrie to his brother, a student of Augustus

De Morgan, in 1852.

The problem concerns planar maps—that is, subdivi-

sions of the plane into nonoverlapping regions bounded

by simple closed curves. In geographical maps it has been

observed empirically, in as many special cases as have been

tried, that, at most, four colours are needed to colour the