Graziani F. (editor) Computational Methods in Transport

Подождите немного. Документ загружается.

Diﬀerent Algorithms of 2D Transport 491

Computation

Ideal

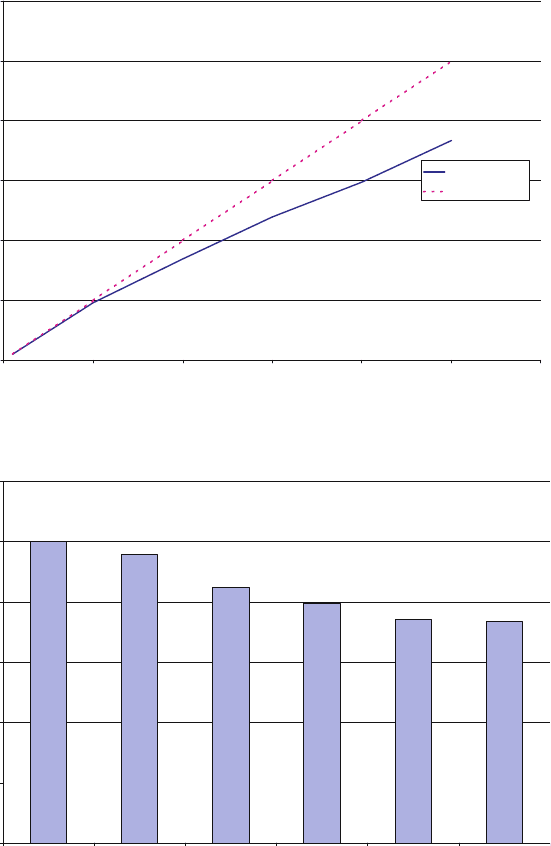
0102030405060

Fig. 3. Speedup dependence on the number of processors

100

95.7

84.7

79.6

74.3

73.4

11020304050

100

120

Fig. 4. Dependence of the parallelization eﬃciency on the number of processors

492 R.M. Shagaliev et al.

Table 3. Speedup and parallelization eﬃciency in the second computation series

Number of Processors Speedup Parallelization

Eﬃciency

1 1 100

10 9.6 95.7

20 16.9 84.7

30 23.9 79.6

40 29.7 74.3

50 36.7 73.4

algorithm (combined) combines both the parallelization by space and en-

ergy variables.

When a multi-group transport equation is being sold, the computations of

the intervals or groups of intervals by the energy variable can be carried out

independently, each on a separate processor or a group of processors. Further

on, such groups of interval are called “group-domains”. Such an approach

allows to use a considerable number of processors at solving a 2D kinetic

equation, reasonable eﬃciency kept.

Numerical investigations of the combined parallelization algorithm eﬃ-

ciency were carried out at three model problems. The method of problem

splitting was applied for computing the speedup and the parallelization ef-

ﬁciency. For this method the main parameters of the parallelization were

calculated using the following formulae:

The speedup:

where

is the average time of the problem computing at one processor when N

processors are run;

is the time of the problem computing at one processor;

The parallelization eﬃciency:

∗

∗ 100 .

For the ﬁrst computation series one hemi-spherical space-domain model

problem had been selected as a test one: 80 rows were homogenously distrib-

uted at the radius, 200 columns were homogenously distributed at the angle.

The order of the angle quadrature was 12, in total there were 96 directions

of the particles motion. Number of energy groups was 28.

The result speedup and the parallelization eﬃciency are presented in Ta-

ble 4. The total number of processors, as well as the number of para-domains

Diﬀerent Algorithms of 2D Transport 493

Table 4. Speedup (Sp) and the parallelization (E) eﬃciency in the ﬁrst test com-

putation series

Number of Number of Group- Number of Para-

Processors Domains Domains Sp E,%

1 1 1 1 100

4413.589

7715.578

10 1 10 11.6 116

14 14 1 8.8 63

25 1 25 25.4 102

28 28 1 12.3 44

40 4 10 39.5 99

50 1 50 43.9 88

at parallelization by space and the number of group-domains at paralleliza-

tion by groups, are shown for each run.

The two-space-domain model problem for the second computation se-

ries was obtained from the previous problem by means of splitting into rows.

Two space-domains. In each space-domain the number of rows was 40,

homogenous by the radius, the number of columns was 200 homogenous by

the angle. The number of energy groups and other parameters of the problem

coincide with those of the one-space-domain problem. The incoming ﬂow on

the outer edge of the ﬁrst space-domain, corresponding to the temperature

1, was taken as the boundary condition.

The speedup and the parallelization eﬃciency, obtained in the course of

numerical research for diﬀerent numbers of para-domains and group-domains,

are presented in Table 5.

Table 5. The speedup (Sp) and the parallelization eﬃciency (E) in the second test

computation series

Number of Number of Group- Number of Para-

Processors Domains Domains Sp E, %

1 1 1 1 100

10 1 10 9.4 94

25 1 25 20.7 83

40 4 10 31.1 78

50 1 50 36.6 73

494 R.M. Shagaliev et al.

The three-space-domain model problem for the third computation se-

ries was obtained from the previous two-space-domain problem by means of

splitting the ﬁrst space-domain into columns.

Three space-domains. In the ﬁrst and the second ones the number of

rows was 40, homogenous by the radius, the number of columns was 100,

homogenous by the angle. In the third space-domain the number of rows

was 40, homogenous by the radius, and the number of columns was 200,

homogenous by the angle. The number of energy groups and other parameters

coincide with those of the one-space-domain problem. The incoming ﬂow on

the outer edges of the ﬁrst and the second space-domains, corresponding the

temperature 1, was taken as the boundary condition.

The speedup and the parallelization eﬃciency, obtained in the course of

numerical research for diﬀerent numbers of para-domains and group-domains,

are presented in Table 6.

Table 6. The speedup (Sp) and the parallelization eﬃciency (E) in the third test

computation series

Number of Number of Group- Number of Para-

Processors Domains Domains Sp E, %

1 1 1 1 100

10 1 10 7.5 75

25 1 25 20.3 81

40 4 10 24.9 62

50 1 50 34.9 70

Nowadays the most perfect parallelization algorithm is the one where

the matrix decomposition of the initial system is used. Unlike splitting the

system only into columns, here the space-domain was cut both into columns

and rows.

The main principles of the algorithm of minor block parallelization were

as follows:

• Application of spatial decomposition of the space-domain into para- do-

mains, the space-domain was split into columns and rows;

• The system of grid equations was solved independently by the angle vari-

able;

• Each para-domain of the current direction was solved with inner boundary

conditions, computed at the current iteration, which allows to keep the

solution precision and does not increase the total number of iterations

comparing with the step-by-step method;

• Complete integration of inter-processor data exchange with the computa-

tion, achieved by the application of asynchronous receive/send operations.

Diﬀerent Algorithms of 2D Transport 495

A one-space-domain spherically symmetrical transport problem in the

one-group iteration was used as a test problem for the investigations of the

eﬃciency of the matrix decomposition method for solving 2D transport equa-

tions. The spatial grid comprised 1200 rows and 1200 columns. The problem

was computed on the angular grid with 6, 8, 12 and 14 intervals by µ for

the analysis of the inﬂuence of the interval numbers on the parallelization

eﬃciency. There were 5 computation steps with 6 iterations in each one. The

number of processors was selected so that the computation was balanced,

that is the number of calculated points was equal on each processor at a

time. The speedup and the parallelization eﬃciency are presented in Tables

7–10.

Table 7. Parallelization eﬃciency at µ =6

Np Time Sp En, %

1 3381.12 1.00 100.00

50 118 29 57.01

Table 8. Parallelization eﬃciency at µ =8

Np Time Sp En, %

1 5402.21 1.00 100.00

50 160 34 67.05

Table 9. Parallelization eﬃciency at µ =12

Np Time Sp En, %

1 10717.53 1.00 100.00

50 274 39 78.23

Table 10. Parallelization eﬃciency at µ =14

Np Time Sp En, %

1 13882.33 1.00 100.00

50 350 40 79.28

496 R.M. Shagaliev et al.

The following conclusion can be drawn out basing on the presented ma-

terial:

• Application of the combined parallel algorithm, that is the combination of

matrix geometrical and energy decomposition, is the most eﬃcient one for

solving the 2D multi-group transport equations, as extra possibilities for

balancing the computation load on processors occur.

Part V

Neutron Transport

Parallel Deterministic Neutron Transport

with AMR

C.J. Clouse

Lawrence Livermore National Laboratory, Livermore CA

clouse1@llnl.gov

AMTRAN, a one, two and three dimensional Sn neutron transport code

with adaptive mesh reﬁnement (AMR) has been parallelized with MPI over

spatial domains and energy groups and with threads over angles. Block reﬁned

AMR is used with linear ﬁnite element representations for the ﬂuxes, which

are node centered. AMR requirements are determined by minimum mean

free path calculations throughout the problem and can provide an order of

magnitude or more reduction in zoning requirements for the same level of

accuracy, compared to a uniformly zoned problem.

1 Introduction

AMTRAN, a two and three dimensional Sn neutron transport code designed

to run eﬀectively on large parallel machines that have both distributed mem-

ory and shared memory parallelism, ﬁrst began development in 1995 under

an industrial partnership agreement with several oil well logging companies

and LLNL. Due to shortened time lines and dwindling DOE funding in sup-

port of industrial partnership agreements, AMTRAN never became a major

contributor in oil well logging calculations. However, it was recognized as

an excellent R&D test bed for trying out new parallel algorithms and AMR

techniques as applied to the Boltzmann equation. Development has continued

over the years and, although the code and its algorithms have been presented

at several conferences [1, 2] this is the ﬁrst publication of the basic code and

it’s techniques. At the time development began in 1995, the notion of apply-

ing AMR techniques to neutron transport problems was unexplored. Since

that time, a number of other AMR neutron transport codes have been devel-

oped [3,4]. AMTRAN, however, remains unique in its combination of degrees

of parallelism (MPI in space and energy and threading in angle) and its use

of ﬁnite element node centered ﬂuxes (the other referenced AMR codes use

face or zone centered ﬂuxes). As in the case of hydrodynamics, where spatial

AMR was ﬁrst developed, many transport applications have widely varying

resolution needs within the same application. Stability and accuracy consid-

erations require that spatial zoning be able to resolve length scales less than a

neutron mean-free-path for most commonly used algorithms. This can be on

the order of a millimeter in ﬁssionable materials of nominal density to a meter

500 C.J. Clouse

or more in air. An example of particular interest in our work is the interro-

gation of cargo containers for ﬁssionable material using a 14 MeV neutron

source. The cargo container could be a semi-tractor trailer with the neutron

source situated on one side of the trailer and a detector located on the op-

posite side. The goal is to be able to match the detector signal with known

conﬁgurations of various types of ﬁssionable materials. In this example, the

distance between source and detector could be many meters; the material

throughout most of which is probably air or some other material that is rela-

tively transparent to neutrons, but the ﬁssionable target would require good

spatial resolution. Spatial AMR allows us to get the needed resolution in the

target without making the overall calculation unwieldy.

2CodeOverview

AMTRAN operates in 2D cylindrical and 3D cartesian geometries. Node cen-

tered ﬂuxes are represented with continuous linear ﬁnite elements, similar to

the methods employed by Greenbaum and Ferguson [5]. Angular discretiza-

tion in 2D and 3D is with standard discrete ordinates and, therefore, requires

half angle approximations to maintain acceptable conditions on the ordinates

when ﬁnite diﬀerencing the angular derivative in cylindrical coordinates (see

[6] for a discussion of this topic). In 1D, a quadratic ﬁnite element approxima-

tion for the angular unknown has been implemented and provides signiﬁcant

computational savings over standard diﬀerencing (see [7] for a detailed dis-

cussion). AMTRAN has several simple internal generators: nested spheres

with point to point linearly interpolated densities, nested cylinders with con-

stant densities and constant density cartesian blocks. It is also capable of

reading COG [9] input and using the geometry generator routines in COG

to construct a mesh.

2.1 Production of AMR Blocks

The AMR algorithm in AMTRAN is block based and thus produces a hexahe-

dral (quadrilaterals in 2D) block decomposition of the problem domain. Like

previous AMR work in the ﬁeld of hydrodynamics, e.g. Berger and Colella

[8], the zone size in each direction is halved for each increase in level of reﬁne-

ment, unlike most hydrodynamic AMR techniques, though, no level nesting

is required, i.e. it is possible to have adjacent blocks diﬀer by any power of 2

in zoning, as illustrated in Fig. 1. Uniform zoning within a block allows fast

and eﬃcient computation of the transport equation.

The reﬁnement criteria is based on neutron mean free path considerations,

h<min







(1)

Parallel Deterministic Neutron Transport with AMR 501

Fig. 1. 2D example where dashed lines indicate block boundaries

where λ

is the minimum neutron mean free path by energy group, h is the

zonal width and a

is a user deﬁned multiplier, which can vary with energy

group. Blocks are created by beginning at the ﬁnest level and tagging all

zones that need to remain at that level. The tagged zones are boxed up using

a “smart bisection” algorithm that can be brieﬂy described as follows for 3D

with the obvious extension to 2D.

Count up all the tagged zones in each 2D plane of the problem. Let y

represent the number of tagged zones in plane i, then deﬁne f

to be the

discrete function f

= y

The splitting plan, i = isplit, is chosen such that

isplit =max





f(x

i+1

) −

f(x

)





(2)

where the second derivatives are deﬁned using a standard central diﬀerence

formula,

f(x

) ≡ f (x

i+1

) − 2f(x

)+f(x

i−1

)(3)

A block is subject to further splitting until it satisﬁes one of two condi-

tions: 1) it no longer contains any tagged zones, in which case it is discarded,

or 2) it satisﬁes the following condition,

number of tagged zones

total number of zones

≥ irattag

where irattag is a user speciﬁed eﬃciency ratio. Generally, more and smaller

blocks will be produced as the value of irattag is increased.

2.2 Sweeping the Mesh

The time-dependent transport equation can be written as follows,