Graziani F. (editor) Computational Methods in Transport

Подождите немного. Документ загружается.

Use of the Space Adaptive Algorithm

to Solve 2D Problems of Photon Transport

and Interaction with Medium

A. V. Alekseyev, R. M. Shagaliev, I. M. Belyakov, A. V. Gichuk,

V. V. Evdokimov, A. N. Moskvin, A. A. Nuzhdin, N. P. Pleteneva,

and T. V. Shemyakina

1 Introduction

Numerical simulation of multidimensional particle transport processes is

among the most diﬃcult problems in applied mathematics with high compu-

tational burden. Deterministic methods are widely used at present time for

solving transport equations numerically. Further development of such meth-

ods opens a prospect for simulating various physical processes of particle

and energy transport in more realistic assumptions and with more accurate

and profound consideration of details and speciﬁc features of the particular

problems.

One of the main diﬃculties of solving a multidimensional transport equa-

tion numerically is that the number of variables required for adequate sim-

ulation of a given system may be large enough. In particular, a 2D time-

dependent transport equation should be solved in 6D phase space and a 3D

equation – in 7D phase space [1].

When developing the particular deterministic numerical methods for mul-

tidimensional transport equations, stringent requirements of memory and

cost-eﬃciency of the numerical methods for solving large-size grid equations

are imposed. Another problem of simulating a transport equation numeri-

cally consists in that it is often required to solve the equation in complex

geometry with sub-regions essentially diﬀering in their optical properties. In

so doing, the dependence of the transport equation factors describing the ra-

diation/medium interaction on the transport equation solution is essentially

nonlinear. However, introduction of a ﬁne spatial grid in the computational

domain as a whole is not required, moreover, such grid signiﬁcantly increases

the problem run time and the requirement of memory resources.

The paper describes the results of eﬀorts on development and numerical

studies of the space adaptive method for numerically solving multidimen-

sional transport equations under the contract with LANL [2]. The space

adaptive sub-grid method for solving a 2D time-dependent multiple-group

transport equation is described. The idea of the adaptive method is that

every time step some multiply connected, in general, sub-domain is deter-

mined by examining grid solutions in mathematical regions of the problem

to be solved, where the numerical solution to the transport equation has to

236 A.V. Alekseyev et al.

be found with a higher precision. Within the sub-domain above, the original

(reference) grid cells are fragmented into smaller cells according to certain

prescribed rules. The transport equation is approximated separately for each

small cell to provide the required higher precision of numerical solution. The

number of reference grid’s cells contained in the sub-domain above is consid-

erably less, as a rule, than the total number of the reference grid’s cells. This

also provides a relative cost-eﬃciency of computations using adaptive grids

of such a kind.

2 Statement of a 2D Transport Equation

The method is based on the kinetic multiple-group model describing the

radiation transport processes using the classic divergent form of a 2D time-

dependent transport equation. The equations are as follows [1,3]:

∂ε

∂t

+ Lε

+ χ

2π

(0)

2π

, (1)

i =1,...,i1isthegroupnumber,

Lε

= µ

∂ε

∂z

∂

∂r



r ·

1 − µ

· cos ϕε



−

∂

∂ϕ



1 − µ

· sin ϕ · ε



, (2)

∂E

∂t



i=1

· ε

(0)

∆ω

−



i=1

∆ω

(3)

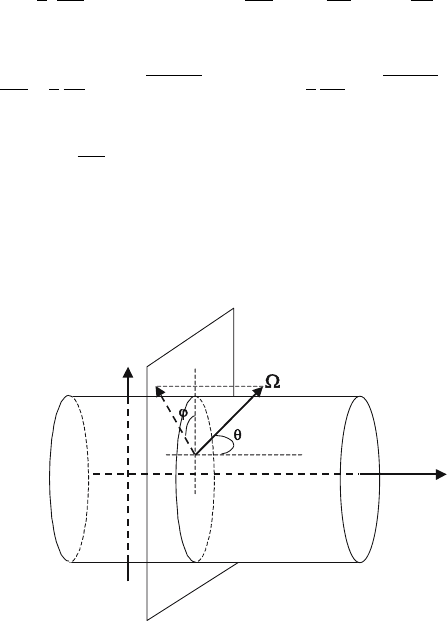
The equation has to be solved in the axially symmetric domain D =

{(r, z) ∈ L},whereL is the cross section of the solid of revolution by a plane

passing across Z-axis (Fig. 1).

Fig. 1. Transport problem geometry

Use of the Space Adaptive Algorithm to Solve 2D Problems 237

The following table of symbols is used to write the equations:

r, z are cylindrical coordinates of a particle (Fig. 1);

→

Ω

(µ, ϕ) is a unit vector in the direction of the particle ﬂight

(Fig. 1);

µ =cos(θ);

θ is an angle between vector

→

Ω

and axis of symmetry z

(Fig. 1);

ϕ is an angle between the projection of vector

→

Ω

to the

plane passing through point (r, z) normally to Z-axis

and the vector joining points (0,z)and(r, z) (Fig. 1);

−1 ≤ µ ≤ 1, 0 ≤ ϕ ≤ π;

= ε

(r, z, µ, ϕ, ω

,t) is the radiation intensity function (the desired func-

tion),

is mean energy of photons in group i,

∆ω

is width of the interval with respect to energy variable

ω,

T = T (r, z) is temperature of medium,

E = E(ρ, T ) is internal energy,

= χ

(ρ, T, ω

) is absorption cross-section,

= Q

(r, z, ω

) is an independent source,

= χ

(ρ, T, ω

) is scattering cross-section,

= χ

+ χ

is full cross-section,

= ε

(T,ω

) is Planck function,

= Q

(r, z, ω

) is an independent source.

Photon absorption and scattering processes are taken into account.

Processes of energy re-emission by a medium are simulated in approxima-

tion to local thermodynamic equilibrium (using Planck function).

The boundary condition on the outer surface is speciﬁed in the form

ε (t, r, z, µ, ϕ)

(r,z)∈Γ

= φ(t, r

,µ,ϕ)(4)

with



→

Ω

∗

→



< 0. Here, Γ is generatrix of the solid of revolution;

→

is the

outer normal to generatrix Γ; φ(t, r

,µ,ϕ) is the speciﬁed function (a ﬂow

of particles entering into the solid of revolution).

Besides, the system of (1)–(4) is supplemented with initial conditions in

time-dependent case.

Note that only one-group transport equation will be considered in the

subsequent description. Of course, the transport equation solution scheme in

238 A.V. Alekseyev et al.

a one-group case will essentially correspond to the multiple-group one in all

variables except for the energy variable.

3 Description of 2D Transport Equation

Approximation Methods

To approximate the transport equation in angular variables, DS

-type

schemes [1, 3–5] are used. In space variables, the transport equation is ap-

proximated using the so-called “extended template” [6].

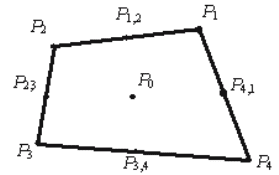
Consider region L covered with the quadrangular spatial grid. Introduce

the grid values of function ε at nodes (ε

), on edges (ε

l,l+1

) and at the

centers of quadrangles (ε

) ( Fig. 2).

Fig. 2. 2D cell

The algorithm of solving the system of grid equations with the speciﬁed

right-hand side of the transport equation is described below. For some ﬁxed

value of parameter µ

m−1/2

, the grid equations are solved successively for each

value of ¯ϕ

q,m

(q =1, 2,...) beginning from ϕ = π. Then, the system of bal-

ance equations is solved in combination with the additional equations, initial

and boundary conditions for the chosen direction µ

m−1/2

, ¯ϕ

q−1/2,m−1/2

.If

the right-hand side of the transport equation is known, the system can be

reduced to the system with the triangle matrix according to the algorithm de-

scribed in [1], i.e. it is solved using the sweep (point-to-point) computational

algorithm.

4 Description of the Space Adaptive Computational

Algorithm for Transport Equation

The idea of the multiple-grid method considered in the paper is that every

time step some sub-domain (a multiply connected one, in general) is selected

by examining the grid solutions in computational domains of the problem,

where the numerical solution to the transport equation has to be found with a

Use of the Space Adaptive Algorithm to Solve 2D Problems 239

higher accuracy. Spatial cells of such sub-domain are partitioned into smaller

cells according to the certain rules.

In so doing, there emerges a possibility to reﬁne spatial cells belonging

to that space sub-domain only, where a higher-accuracy numerical solution

is desired. The set of the reference spatial grid cells to be reﬁned is variable.

Note the main features of the multiple-grid method under consideration

for solving 2D transport problems.

(1) During each time step, some sub-domain (subset of spatial cells), which

is a multiply connected one, in general, is selected with regard to the

particular features of the problem stated by examining grid solutions in

computational domains of the problem, where the numerical solution to

the X-ray transport equation has to be found with a higher accuracy.

The analysis of gradients of the grid solution to the transport equation

from the previous time step is performed to estimate the set of cells.

(2) Each space cell of the selected sub-domain is fragmented into smaller

cells according to the prescribed rules. One and the same reference cell

can be fragmented into various numbers of smaller cells, or it can be not

fragmented at all. The transport equation is approximated separately in

each of the smaller cells to provide a higher-accuracy numerical solution.

(3) The system of grid radiation transport equations is solved numerically

using the implicit sweep (point-to-point) computational scheme. The or-

der of resolving the small cells comprising the reference cell is determined

by the cell exposure. The numerical solution to the transport equation at

the reference cell’s central point can be found using the obtained numer-

ical solutions to the transport equation at smaller cells. In so doing, the

scheme conservativeness is preserved, i.e. the number of photons in the

reference cell remains equal to the total number of photons in all of the

smaller cells within the reference one. The energy equation is also solved

in smaller cells.

The adaptive method under consideration uses the following algorithm of

subdividing spatial cells into smaller ones (Fig. 3). Each of the four edges of

the reference cell is subdivided into equal segments. The opposite edges have

the same number of segments.

The following main ideas underlie the development of the adaptive method

for solving 2D transport equations:

• Each cell of a reference spatial grid can be partitioned into smaller cells of

an adaptive reﬁned grid (adaptive cells).

• The adaptively reﬁned grid is built by partitioning each space direction

into 2

equal intervals, where N is the adaptive grid level.

• The adaptive grid level in rows and columns of a cell may change with

transition from a previous step to the next one.

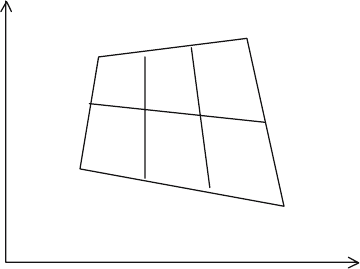
240 A.V. Alekseyev et al.

Fig. 3. The reference cell fragmentation geometry

• The adaptive grid is built at the beginning of a time step basing on exam-

ination of the spatial distribution of the solution function on the reference

spatial grid obtained at the previous time step.

• The geometric parameters of the adaptive grid are calculated and the so-

lution functions are interpolated from the older adaptive grid to the new

one.

• The order of resolving space cells during sweep (point-to-point) computa-

tions using the transport equation solution module is determined on the

reference grid. If a cell is adaptively reﬁned, the subsystem of equations

corresponding to the transport equation approximation on the adaptive

grid of the given cell is solved.

• All the solution functions are stored in the special dynamic data structure

on the adaptive grid, as well as integrated onto the reference grid and

stored in standard arrays.

As it was mentioned above, a space adaptive grid can vary dynamically (it

can be either reﬁned or enlarged) during time steps. Since the values of a set

of functions are stored and calculated in the adaptive grid cells, there occurs a

need in re-interpolating the values of the corresponding grid functions, which

can be determined both at the centers of space cells and on their edges, with

each change of the adaptive grid.

5 Results of Computational Investigations

of the Adaptive Method Performance

5.1 Problem with Analytical Solution

The task is to calculate the process of radiation transport and interaction

with plane 1D medium [7]. Computations for the 1D problem above by a

Use of the Space Adaptive Algorithm to Solve 2D Problems 241

0.5

1000.1

1000.0

Fig. 4. The system geometry

2D code using the transport equation written in cylindrical coordinates were

carried out for the following geometry (Fig. 4).

The incoming radiation ﬂux corresponding to

ε(0,µ,t)=

c +(cC

µ +1)

,µ>0,C

= −0.85903205 ...

where ε(z,µ, t) is the radiation intensity multiplied by π, is speciﬁed at the

left end {Z =0, 1000 ≤ R ≤ 1000.1}

At the right end {Z =0.5, 1000 ≤ R ≤ 1000.1}, the incoming radiation

ﬂux is set equal to zero.

On the upper {0 ≤ Z ≤ 0.5,R= 1000.1} and lower {0 ≤ Z ≤ 0.5,R=

1000} lateral surfaces the boundary condition “mirror reﬂection” is speciﬁed.

As it was mentioned above, the dependences of energy on temperature and

absorption cross-section are considered in the form E = 2058 · T

,χ

2058·T

, respectively.

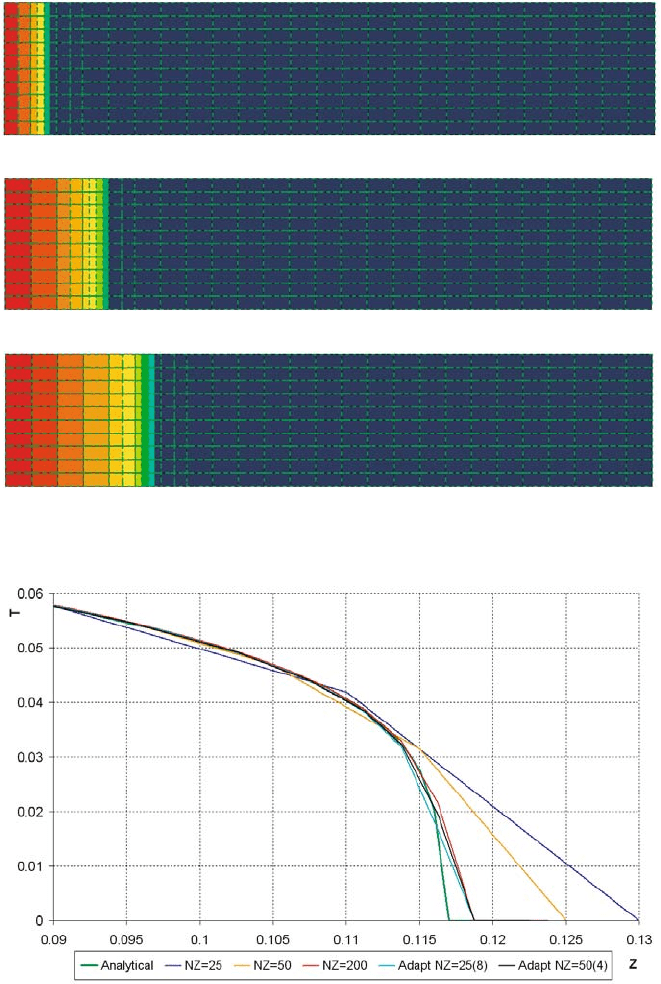
The next ﬁgure (Fig. 5) shows us spatial grids and the distribution in

space of the material temperature values at several times for the reference

grid of 25 columns and with maximum partition into 4 cells. The space grid

concentration is seen near the radiation wave front only, i.e. in the area of

maximum solution gradient. Computations before the wave front and after

it are carried out on the reference space grid, because there are no strong

gradients in solution there. The diﬀerence between the levels of partitioning

the neighboring cells doesn’t exceed 1.

The next ﬁgure (Fig. 6) shows the results of computations with adaptivity

in which the maximum partition of the reference space grid in all its cells

results in 200 intervals in Z variable. These are computations 25(8) and 50(4).

For comparison, the ﬁgure also shows the results of computations without

adaptivity, with 25, 50, and 200 intervals in Z variable.

It is seen that the results of computations with adaptivity appear to be

very close to the one obtained using a ﬁne grid of 200 space cells.

242 A.V. Alekseyev et al.

t=0.03

t=0.07

t=0.1

Fig. 5. Computation results for the reference grid NZ=25 at various times

Fig. 6. Results of comparative computations using various grids

Use of the Space Adaptive Algorithm to Solve 2D Problems 243

Fig. 7. Results of comparative computations for adaptive grids of a higher adapt-

ability level

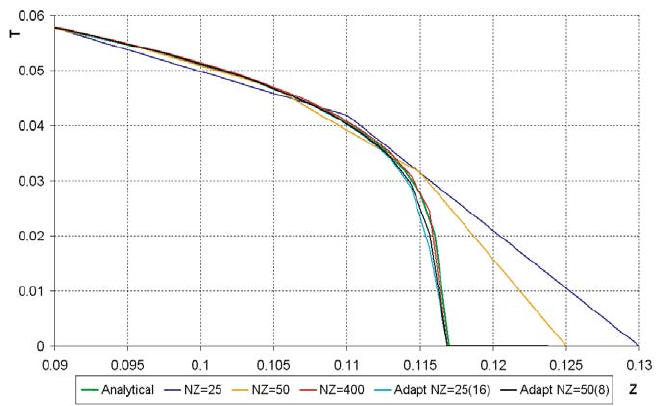
Figure 7 below gives the similar comparison for 400 intervals in Z vari-

able. The material temperature curves, in this case, are given for adaptive

computations 25(16) and 50(8) with maximum partition of the reference cells

into 16 and 8 adaptive cells, respectively.

Though the spatial grid reﬁnement, in this case, takes place in the wave

front passage area alone, computations using the adaptive code actually coin-

cide with that one using the ﬁnest grid of 400 columns and with the analytical

solution, as well. The result conﬁrms the adaptive algorithm operation valid-

ity.

Comparison between the running times shows that the computation with

adaptivity and with maximum partition of the reference grid into 8 cells re-

quires less time (by a factor of 6.2) than the computation using the standard

technique on the space grid of 200 columns, with the results of these com-

putations being actually the same, and the computation with adaptivity and

with maximum partition of the reference grid into 4 cells is 3.1 times faster.

The similar comparison between the standard computations without

adaptivity using the grid of 400 columns and computations with adaptiv-

ity and with partition of reference cells into 16 and 8 adaptive cells shows

that the achieved saving of time is by a factor of 9 and 5.6, respectively, with

the given precision preserved.

244 A.V. Alekseyev et al.

5.2 Results of Computations for the Dense-Layer Problem

There is a cylindrical layer (1.0cm≤ Z ≤ 1.3 cm; 100.0cm ≤ R ≤ 102.0cm)

which consists of one physical region and is R = 100.0 cm distant from Z-axis

of revolution and Z =1.0 cm distant from R-axis (Fig. 8).

T=1

1.3

1.0

100.0

102.0

Fig. 8. The system geometry

The benchmark is based on the modiﬁcation to the well-known three-

region Fleck benchmark [8]. Namely, the benchmark oﬀered below considers

one of the Fleck’s regions (optically dense) with slightly changed dimensions.

Besides, the benchmark oﬀered is solved in one-group “gray matter” approx-

imation.

The following parameters are speciﬁed for the given region:

• coordinate 1.0cm≤ Z ≤ 1.3cm,

• coordinate 100.0cm≤ R ≤ 102.0cm,

• absorption cross-section χ

, where A = 50.890585, T is the material

temperature,

• no dissipation,

• internal energy versus temperature is described by equation E =0.81 ∗ T .

The incoming unilateral radiation energy ﬂux isotropically distributed

over the solid body and correspondent to the radiation temperature T =

1 KeV is speciﬁed on the lower surface (1.0cm≤ Z ≤ 1.3cm, R = 100.0cm).

For the upper surface (1.0cm ≤ Z ≤ 1.3cm, R = 102.0 cm), the bound-

ary condition “free surface” is speciﬁed (zero incoming ﬂux). The boundary

condition “mirror reﬂection” is speciﬁed for lateral surfaces.