Грамагин Е.А. Теория дискретных систем управления
Подождите немного. Документ загружается.

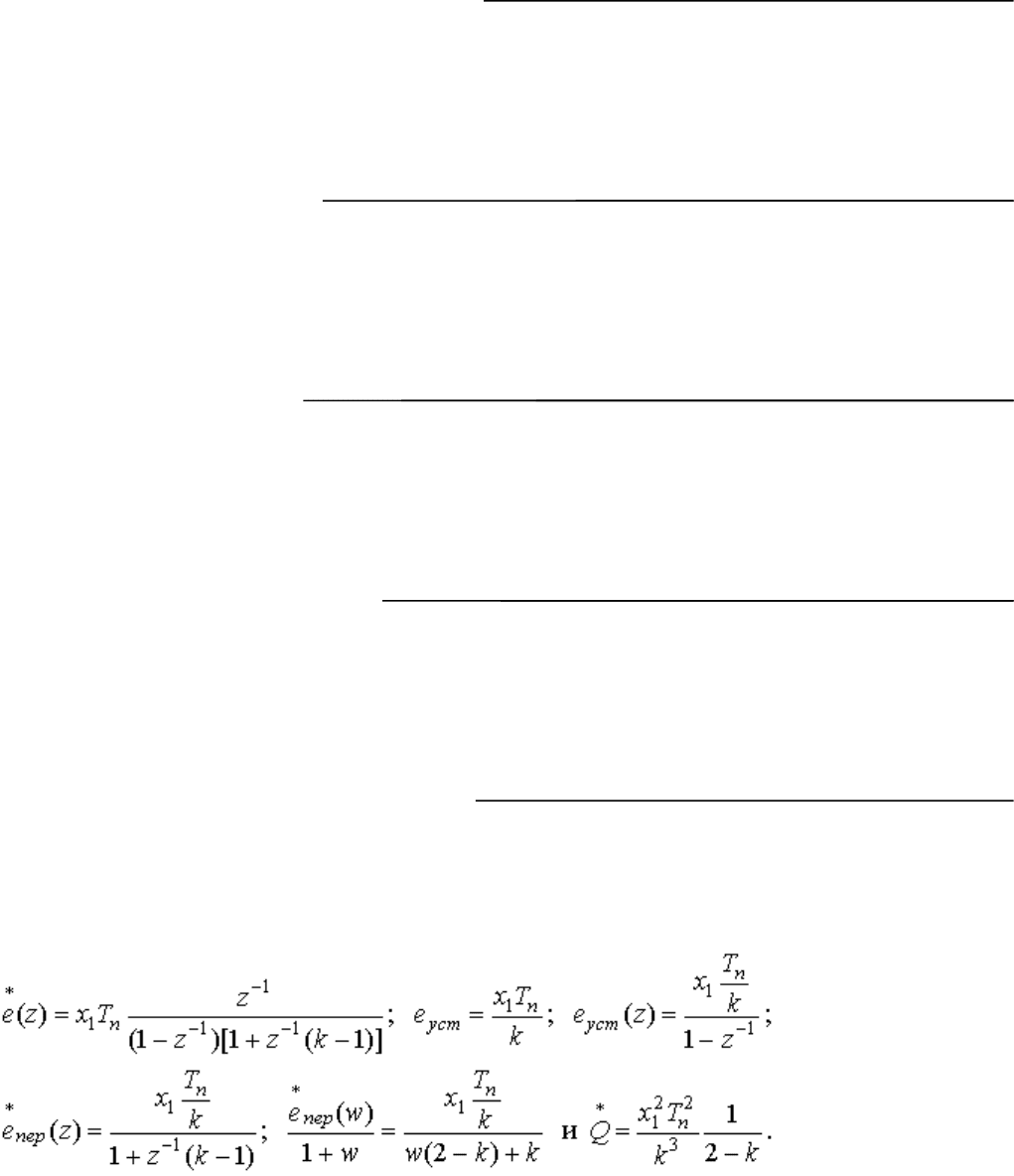
1 - z
-1
1 + z
-1
(k - 1) 1 + z
-1
(k - 1)
Установившееся значение ошибки
e
уст
1=
lim
z → 0
(1 - z
-1
)
x
0
1 + z
-1
(k - 1)
= 0.
Изображения переходной составляющей ошибки
e
*
пер
(z) =
x
0
1 + z
-1
(k - 1)
или e
*
пер
(w) =
x
0
(1 + w)
w(2 - k) + k
.
Отсюда
e
*
пер
(w)
1 + w
=
x
0
w(2 - k) + k
=
α
0
β
1
w + β
0
.
Табулированный интеграл для l = 1 (табл. П.1) равен
I
1
[
α
0
β
1
w + β
0
] =
α
0
2
2(2 - k)k
и квадратичная суммарная оценка
Q* = 2I
1
1=
x
0
2
(2 - k)k
.
Для случая дискретной линейной функции аналогично получим
В обоих случаях Q* принимает бесконечные значения при k = 0 и k = 2, соответствующим границе
устойчивости системы (пример 2.1) и теряет смысл (становится отрицательной) при k < 0 и k > 2,
51
когда система неустойчива. При k = 1 (бесконечная степень устойчивости) квадратичная
суммарная оценка в обоих случаях минимальна.
Так как коэффициент k безразмерен, х
0
1имеет размерность отслеживаемого параметра, а х
1
1- его
скорости, то в обоих рассмотренных случаях размерность Q* равна квадрату размерности
входного процесса. Отметим, что в непрерывных системах квадратичная интегральная оценка
качества переходного процесса имеет размерность квадрата размерности входного процесса,
умноженного на секунду.
2.3. Качество дискретных систем в установившемся режиме при регулярных воздействиях
После окончания переходных процессов в системе наступает установившийся режим, качество
которого в основном зависит от точности отработки задающих воздействий и степени фильтрации
помех. В теории дискретных систем удобным способом оценки качества является оценка
точности, то есть анализ ошибок управления. Эти ошибки зависят от параметров системы, ее
структуры, от характеристик воздействий и в плане математическом определяются вынужденной
составляющей решения разностного уравнения
y
в
(iT
n
) = y
x
(iT
n
) +
M
Σ
j = 0
y
νj
(iT
n
),
где y
x
(iT
n
) и y
ν
(iT
n
) - выходные координаты, определяемые соответственно задающим и
возмущающим воздействиями, и принято, что на линейную систему поступает М помех.
Для следящих систем ошибка управления представляет собой разность
e(iT
n
) = x(iT
n
) - y
в
(iT
n
),
то есть в установившемся режиме она равна
e(iT
n
) = e
x
(iT
n
) +
M
Σ
j = 0
y
νj
(iT
n
), 1 1 1 1 1 1 (2.17)
где y
x
(iT
n
) = x(iT
n
) - y
x
(iT
n
)- ошибка отработки задающего воздействия (динамическая ошибка) и
e
ν
(iT
n
) = - y
ν
(iT
n
)- ошибка от возмущающего воздействия (флюктуационная ошибка, если ν
i
(iT
n
) -
случайные процессы).
Оценка качества установившегося режима производится по значению ошибки (2.17) или
некоторых функций от нее и имеет особое значение, так как у большинства систем (в том числе у
всех следящих) этот режим является основным, определяющим выполнение системой
поставленной задачи. Как и в теории непрерывных систем, исследование точности дискретных
52

систем в установившемся режиме производят для регулярных и случайных процессов,
описывающих как задающие, так и возмущающие воздействия. Регулярными функциями времени
можно аппроксимировать некоторые виды задающих и возмущающих воздействий или их
математические ожидания.
Методика расчета ошибок при регулярных воздействиях справедлива (при определенных
предпосылках) для процессов любого происхождения, поэтому рассмотрим ее на примере оценки
качества дискретной системы при регулярных задающих воздействиях x(iT
n
), имея в виду и тот
факт, что такими воздействиями часто аппроксимируют процессы, соответствующие наиболее
тяжелому или наиболее вероятному режимам работы. Будем полагать, таким образом, что
известными являются закон изменения x(iT
n
), структура и параметры дискретной следящей
системы (рис. 1.16), то есть ее передаточная функция K*(z).
По отношению к установившемуся режиму дискретные системы, как и непрерывные, делятся на
статические и астатические ν-го порядка, где ν = 1, 2, ... для астатических и ν = 0 для статических
систем. Ошибки установившегося режима у этих систем определяются как реакция на типовые
воздействия вида x(t) = x
ν
t
ν
1или x(iT
n
) = x
ν
(iT
n
)
ν
.
Установившееся значение ошибки
e
уст
1=
lim
i → ∞
e(iT
n
)
может быть найдено по z-изображению e*(z) как
e
уст
1=
lim
z → 1
(1 - z
-1
)e*(z)
или для рассматриваемой системы (рис. 1.16)
e
уст
1=
lim
z → 1
(1 - z
-1
) K
*
ex
(z) x*(z) =
lim
z → 1
(1 - z
-1
)
x*(z)
1 + K*(z)
1 1 1 1 1 1
(2.18)
K
*
ex
(z) =
e*(z)
x*(z)
,
где K
*
ex
(z) - передаточная функция ошибки, описываемая формулами (1.32) или (1.37).
Порядок астатизма дискретной следящей системы определяется (см. подраздел 1.8) количеством
суммирующих звеньев или, что одно и то же, количеством сомножителей вида (1 - z
-1
) в
передаточной функции разомкнутой системы, которую на основании формулы (1.31) можно
представить соотношением
53
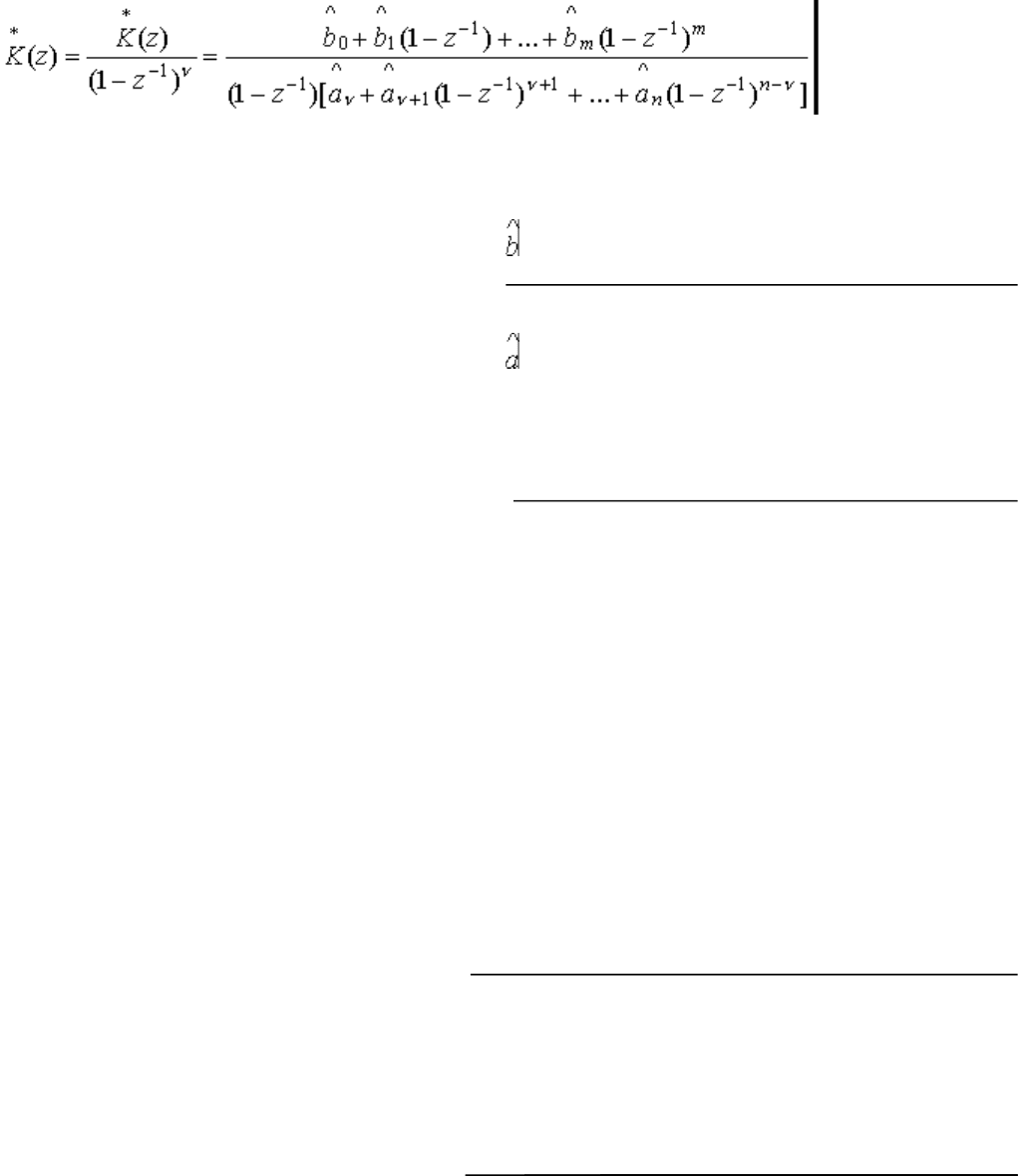
Понятно, что при z = l функция K
*
ν
(z) примет значение, равное коэффициенту преобразования
разомкнутой системы
K
ν
(z) = k
ν
1=
0
ν
,
и, следовательно, формулу (2.20) можно записать в виде
e
уст
1=
lim
z → 1
(1 - z
-1
)
ν + 1
x*(z)
(1 - z
-1
)
ν
1+ k
ν
,
позволяющем определять e
уст
1для системы с различным порядком астатизма при воздействиях типа
x(t) = x
ν
t
ν
При подаче на вход статической системы (ν=0) воздействия х(t) = х
0
11(t), где х
0
1- постоянная
величина с размерностью процесса х(t) с z-преобразованием
x*(z) =
x
0
1 - z
-1
,
установившаяся ошибка в системе принимает значение
e
уст
1=
lim
z → 1
(1 - z
-1
)
x
0
1 - z
-1
1
1 + k
=
x
0
1 + k
.
Если такой же сигнал подать на систему с астатизмом первого порядка (ν = 1), то
e
уст
1= lim
z → 1
(1 - z
-1
)
2
x
0
1
1
= 0.
54
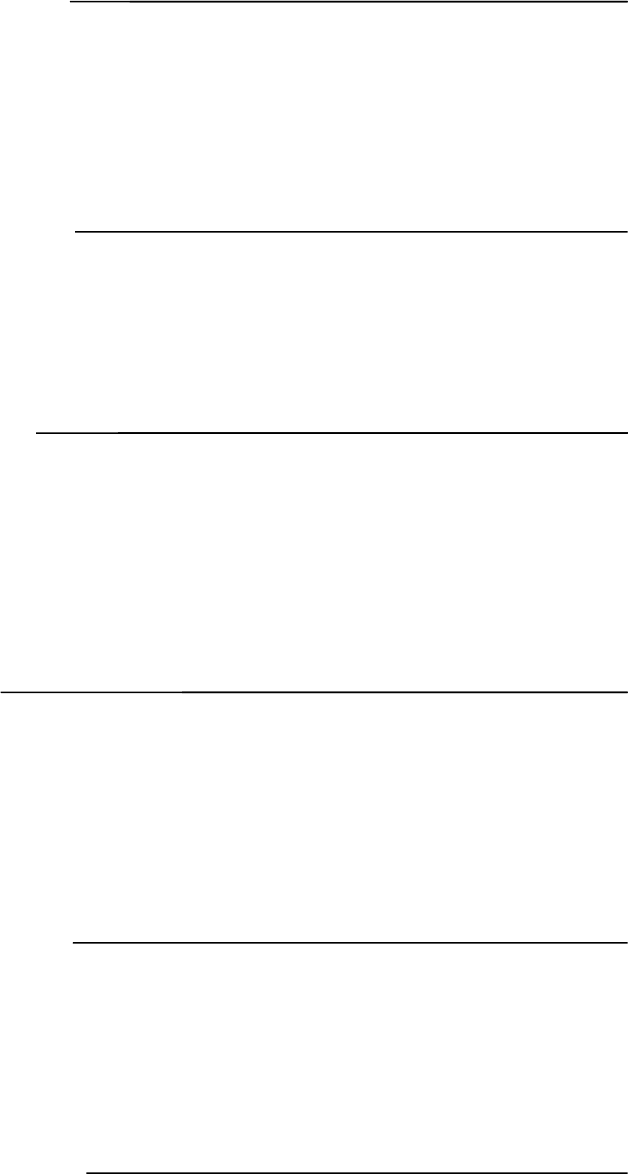
1 - z
-1
(1 - z
-1
) + k
1
При подаче на эту систему воздействия x(t) = x
1
(t), где x
1
1- постоянная с размерностью скорости
сигнала х(t), имеющего z-изображение
x*(z) =
T
n
1z
-1
(1 - z
-1
)
2
(см.табл.П.2), получим
e
уст
1=
lim
z → 1
(1 - z
-1
)
2
T
n
1z
-1
x
1
(1 - z
-1
)
2
1
1
(1 - z
-1
) + k
1
=
x
1
1T
n
k
1
.
Аналогично можно показать, что при подаче сигналов x(t) = x
1
(t) и x(t) = x
0
1(t) на систему с
астатизмом второго порядка (ν = 2) установившаяся ошибка будет равна нулю. Если воздействие
задано в виде
x(t) =
1
2
x
2
1t
2
1или x(iT
n
) =
1
2
,
где х
2
1- постоянная с размерностью ускорения функции х(t), то установившееся значение ошибки
e
уст
1=
x
2
T
n
2
k
2
.
Полученные результаты нетрудно обобщить на системы любого порядка астатизма и убедиться,
что при подаче на систему с астатизмом ν-го порядка воздействия вида
x(t) =
x
ν
1t
ν
ν!
установившаяся ошибка будет равна
e
уст
1= x
ν
1T
n
ν
.
55
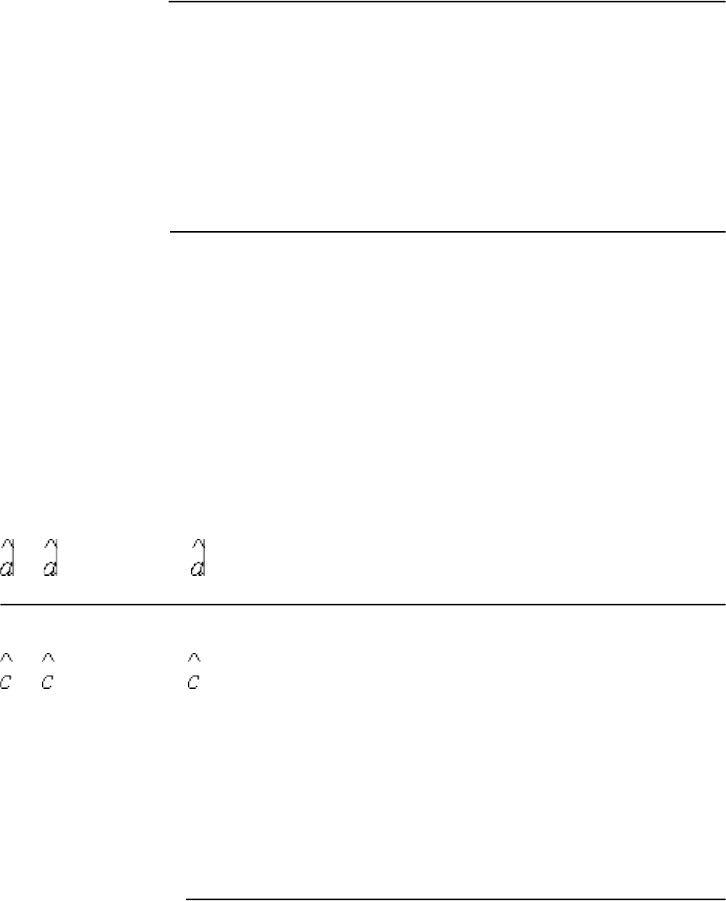
k
ν
Системы астатические ν-го порядка не будут иметь ошибок установившегося режима при подаче
на них воздействий вида
x(t) =
x
ν1
1t
ν
1
ν
1
!
,
если ν
1
1< ν.
В том случае, когда регулярные воздействия описываются более общими выражениями, для
анализа ошибок установившегося режима удобно, как и в непрерывных системах, использовать
коэффициенты ошибок. Методика решения задачи заключается в следующем.
Передаточная функция ошибки K
*
ex
(z) (1.32) представляется в виде ряда
K
*
ex
(z) =
0
1+1
1
(1 - z
-1
) + ... +1
n
(1 - z
-1
)
n
0
1+1
1
(1 - z
-1
) + ... +1
n
(1 - z
-1
)
n
= 1 1 1 1 1 1 (2.19)
= D
0
1+ D
1
(1 - z
-1
) + D
2
(1 - z
-1
)
2
1+ ... ,
который сходится, если z → 1 (i → ∞), то есть если рассматривается установившийся режим. Так
как
K
*
ex
(z) =
e*(z)
x*(z)
,
то из выражения (2.19) можно определить изображение ошибки
e*(z) = D
0
1x*(z) + D
1
(1 - z
-1
) x*(z) + D
2
(1 - z
-1
)
2
1x*(z) + ...
и ее оригинал
e(iT
n
) = D
0
1x(iT
n
) + D
1
Δ
1
x(iT
n
) + D
2
Δ
2
x(iT
n
) + ... 1 1 1 1 1 1 (2.20)
Здесь учтено, что обратное z - преобразование от изображения вида (1 - z
-1
)
k
x*(z) соответствует k-й
конечной разности D
k
Δ
k
x(iT
n
) (см. п.1.4). Составляющие вида в выражении (2.20) называются
ошибками по k-й конечной разности, а коэффициенты D
k
1- коэффициентами ошибок по
соответствующей конечной разности. Ряд ошибки (2.20) сходится, если конечные разности
убывают по абсолютной величине с ростом номера их порядка. Практическое применение ряда
ошибки имеет смысл, если его составляющие убывают быстро (можно ограничиться лишь
56
несколькими первыми членами), что имеет место при медленных значениях функции х(iT
n
), то
есть когда огибающая является медленно меняющимся воздействием .
Таким образом, предпосылками описываемого метода расчета ошибок являются наличие
установившегося режима и узкополосность спектра воздействия, а суть его сводится к
вычислению конечных разностей Δ
k
х(iT
n
) и коэффициентов ошибок D
k
. Методика вычисления
конечных разностей показана в п.1.4, а коэффициенты D
k
, в принципе, могут быть найдены из
соотношения (2.19) путем сравнения коэффициентов при одинаковых степенях двучлена 1 - z
-1
.
Для упрощения записи (2.19), а также для согласования форм записи передаточной функции
ошибки (1.32) и (1.37) вводят подстановку
χ = 1 - z
-1
11 1 1 1 1 1 (2.21)
и тогда формулу (2.19) можно записать следующим образом:
0
1+1
1
χ + ... +1
n
χ
n
1= (
0
1+1
1
χ + ... +1
n
χ
n
)(D
0
1+ D
1
χ + D
2
χ
2
1+ ... ). 1 1 1 1 1 1 (2.22)
Сравнивая в выражении (2.22) коэффициенты при одинаковых степенях χ, нетрудно определить
D
0
1=
0
0
; D
1
1=
1
0
(
1
1- D
0 1
)
; D
2
1=
1
0
(
2
1- D
0 2
1- D
1 1
)
; 1 1 1 1 1 1 (2.23)
D
k
1=
1
0
(
k
1-
k
Σ
j = 1
j
D
k - j
).
Пример 2.4.
Структурная схема следящей системы показана на рис. 1.16. Полагая, что
K(z) =
k z
-1
1 - z
-1
=
P*(z)
Q*(z)
,
оценим точность системы в установившемся режиме, если огибающая задающего воздействия
х(iT
n
) аппроксимируется функцией
x(t) = x
0
1+ x
1
t + 0.5 x
2
t
2
. 1 1 1 1 1 1 (2.24)
Определим вначале конечные разности дискретного задающего воздействия
x(iT
n
) = x
0
1+ x
1
iT
n
1+ 0.5 x
2
(iT
n
)
2
.
Согласно методике, изложенной в п. 1.4, получаем
57
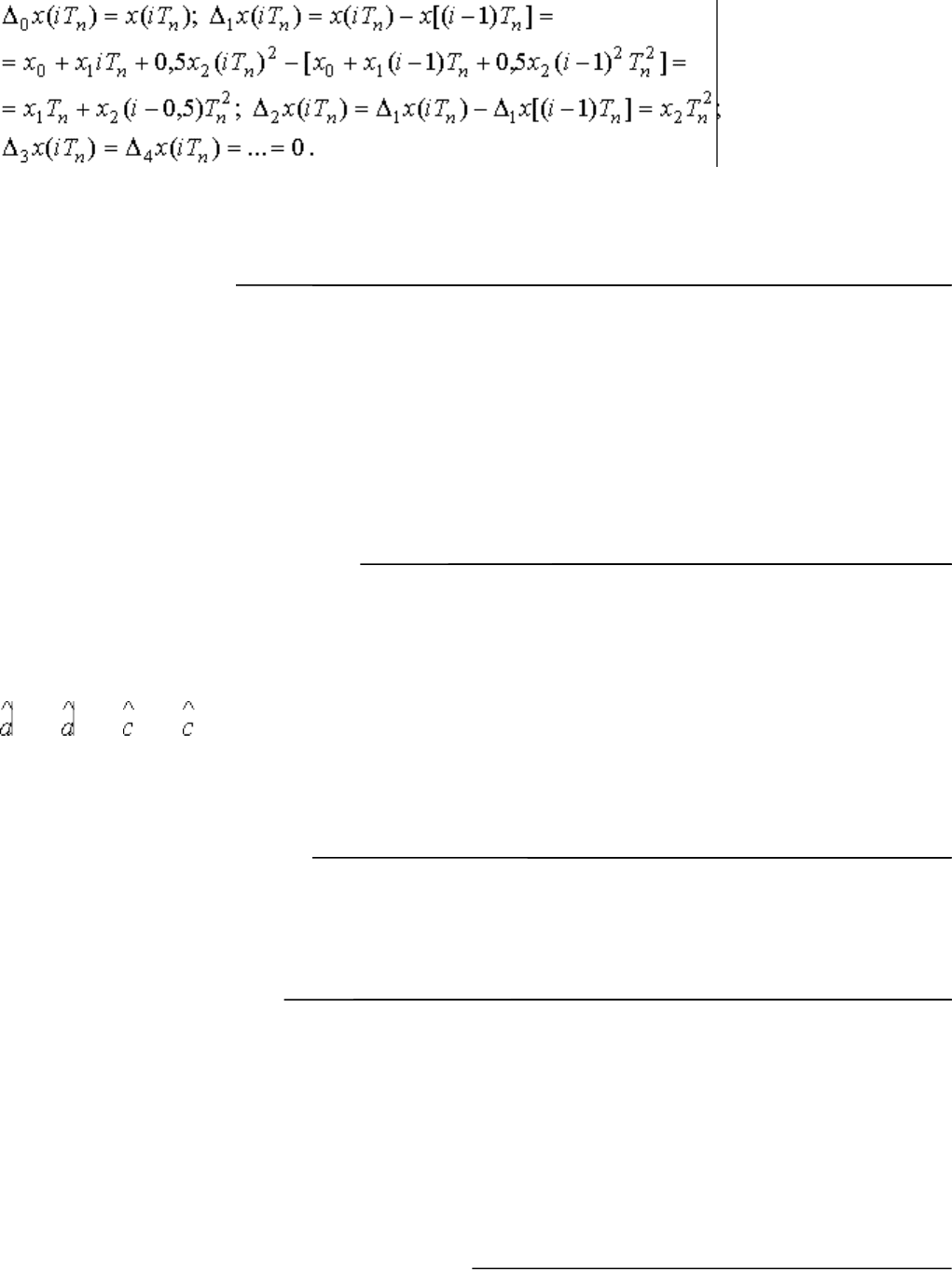
Определим коэффициенты ошибок, для чего запишем
K
*
ex
(z) =
Q*(z)
D*(z)
=
1 - z
-1
1 + (k - 1)z
-1
= D
0
1+ D
1
(1 - z
-1
) + D
2
(1 - z
-1
)
2
1+ ...
Введем подстановку (2.21) и получим
χ = [k + χ(1 - k)](D
0
1+ D
1
χ + D
2
χ + ...),
откуда после сравнения коэффициентов при χ
0
, χ
1
, χ
2
, χ
3
1находим
D
0
1= 0; D
1
1=
1
k
; D
2
1= -
1 - k
k
2
; D
3
1=
(1 - k)
2
k
3
.
Этот же результат можно получить и по формуле (2.23) для
0
1= 0;1
1
1= 1;1
0
1= k;1
1
1= 1 - k.
Ряд ошибки (2.20) для рассматриваемого примера запишется в виде
e(iT
n
) =
1
k
[x
1
T
n
1+ x
2
(i - 0.5)T
n
2
] -
1 - k
k
x
2
T
n
2
1=
T
n
k
x
1
1+
T
n
k
x
2
[(i - 0.5)T
n
1+
k - 1
k
T
n
].
Установившаяся ошибка нарастает со временем за счет ускорения сигнала (2.24), не
компенсируемого системой с одним дискретным интегратором. Это нарастание тем интенсивнее,
чем больше период T
n
и ускорение x
2
1и чем меньше коэффициент преобразования, который по
условиям устойчивости (см. пример 2.1) меняется в пределах 0 < k < 2. Если ускорение x
2
1= 0, то
e(iT
n
) = e
уст
1= T
n
x
1
.
58
k
Этот результат для систем с астатизмом первого порядка получен в начале подраздела.
2.4. Статистический анализ точности в установившемся режиме
В предыдущем подразделе предполагалось, что воздействия, поступающие на систему, являются
регулярными функциями времени и, следовательно, ошибка управления e(iT
n
), определяемая
соотношением (2.17), тоже имеет регулярный характер. На практике подавляющее большинство
возмущающих и задающих воздействий являются случайными, и поэтому ошибка e(iT
n
) -
случайная функция дискретного времени iT
n
, которую можно представить суммой
математического ожидания и центрированной случайной составляющей, то есть
e(iT
n
) =1<e(iT
n
)>1+ e
0
(iT
n
).
Математическое ожидание1<e(iT
n
)>1представляет собой регулярную функцию Времени, методика
его определения показана в п.2.3. Случайная составляющая ошибки, как и в непрерывных
системах, оценивается по величине ее дисперсии
D
e
(iT
n
) =1<[e
0
(iT
n
)]
2
>.
Рассмотрим методику решения задачи в предположении, что все воздействия представляют собой
эргодические стационарные процессы, статистически не зависящие друг от друга. В этом случае
дисперсия ошибки
D
e
(iT
n
) = D
e
определяется из (2.19) соотношением
D
e
1= D
ex
1+
M
Σ
j = 0
D
eνj
,
где D
ex
1и D
eν
1- соответственно дисперсия динамической и флюктуационной ошибок. Так как
методика вычисления составляющих дисперсии одинаковая, то рассмотрим ее на примере
нахождения дисперсии ошибки отработки задающего воздействия.
Определение величины дисперсии дискретного процесса производится (как и в случае
непрерывных систем) по его корреляционной функции, которая для стационарных процессов
определяется как
R
ex
(kT
n
) =1<e
x
0
(iT
n
) e
x
0
(iT
n
1+ kT
n
)>,
или по спектральной плотности - z-преобразованию от корреляционной функции
S
*
ex
(z) =
∞
Σ
k = -∞
R
ex
(kT
n
) z
-k
.
59
Обратное z-преобразование от спектральной плотности определяет корреляционную функцию и
поэтому
D
ex
1= R
ex
(0) =
1
2 π j
|z|=1
S
*
ex
(z) z
-1
1dz. 1 1 1 1 1 1 (2.25)
Для вычисления дисперсии ошибки надо знать, следовательно, статистические характеристики
R
ex
(kT
n
) или S
*
ex
(z), которые зависят от статистических характеристик задающего воздействия
R
x
(kT
n
) и S
*
x
(z), структуры и параметров системы. Отметим, что корреляционная функция R
x
(kT
n
)
и спектральная плотность S
*
x
(z) дискретного процесса x(iT
n
) несут ту же информацию о случайном
процессе, что и в теории непрерывных систем. Корреляционная функция R
x
(kT
n
) представляет
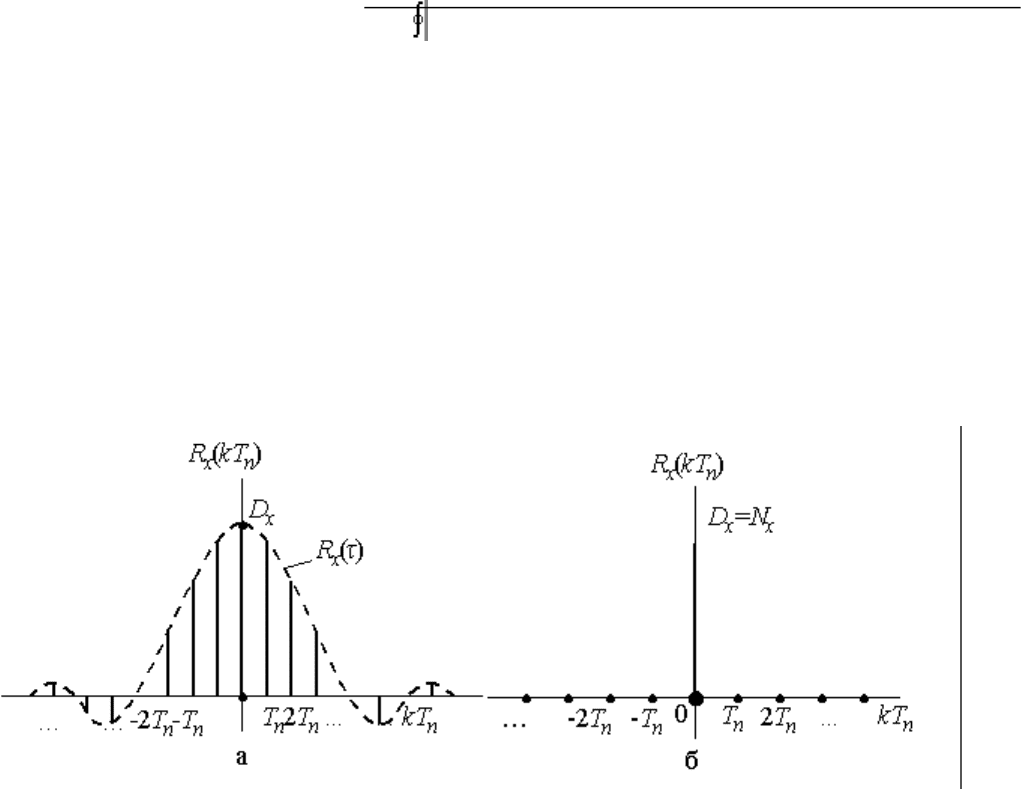
собой дискретную функцию своей огибающей R
x
(τ) ( рис. 2.10, а), то есть может быть получена из
последней подстановкой
τ = kT
n
,
где k - целые числа.
Рис.12.10. Корреляционная функция дискретного случайного процесса (а) и дискретного белого
шума (б)
При исследовании систем важную роль играют случайные величины с некоррелированными
значениями - белый шум. Дискретный белый шум определяется корреляционной функцией (рис.
2.10,б)
R
x
1(kT
n
) = {
D
x
1при k = 0
0 при k ≠ 0
где D
x
1- дисперсия процесса, совпадающая по значению с интенсивностью N
x
1непрерывного
белого шума, являющегося образующей дискретного. Спектральная плотность дискретного белого
шума не зависит от частоты и равна постоянной величине N
x
.
Спектральную плотность ошибки по задающему воздействию S
*
ex
(z) можно представить
произведением
60
