Грамагин Е.А. Теория дискретных систем управления

Подождите немного. Документ загружается.

Однородное разностное уравнение в оригиналах, определяющее переходную составляющую:

(iT

) - (1 - k)y

[(i-1)T

] = 0 или

(iT

) = (1 - k)y

[(i-1)T

Решение этого уравнения при

(-iT

) = 0 и y

(0) = A

записывается в виде

(iT

) = (1 - k)A

; (1 - k)

; ... ;

(iT

) = (1 - k)

;

и для различных значений коэффициента k приведено на рис. 2.4. Если k = 0 или k = 2, то

переходная составляющая не затухает. При k = 0.5 процесс имеет затухающий апериодический, а

при k = 1.5 - затухающий колебательный характер. Если k = 1, то переходный процесс в системе

практически отсутствует (заканчивается к первому периоду). Таким образом, условие

устойчивости

lim

i = 0

(iT

) = 0

соблюдается в исследуемой системе при 0 < k < 2. 1 1 1 1 1 1 (2.7)

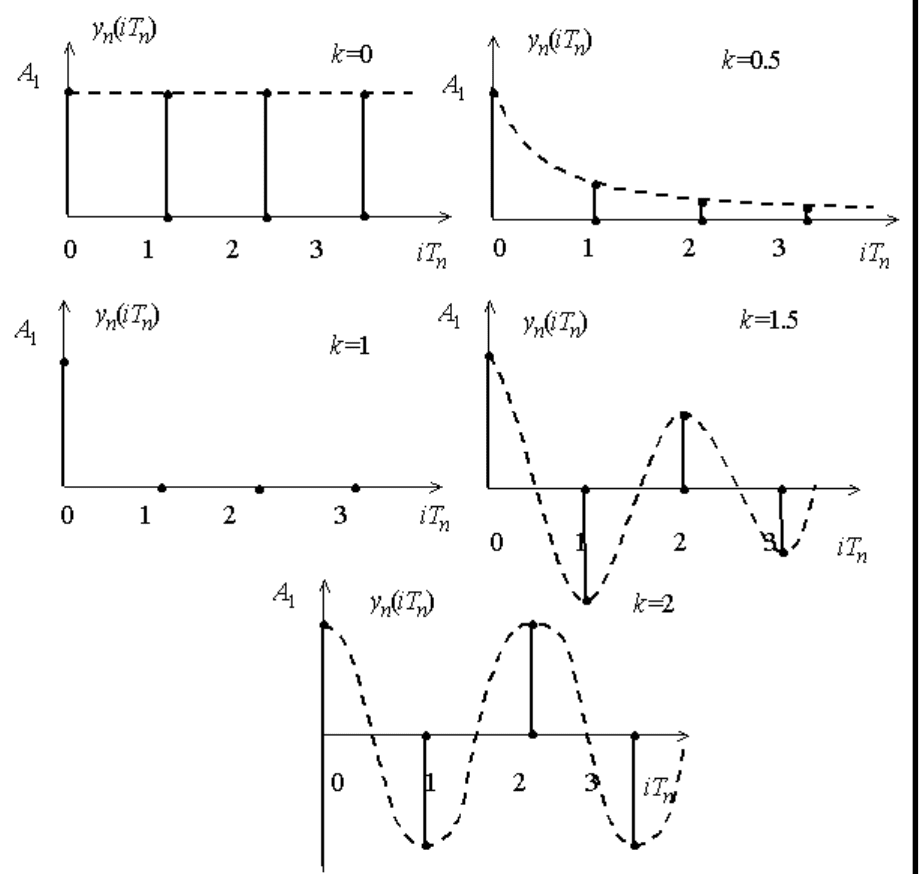
Рис.12.4. Переходные процессы в дискретной системе при различных коэффициентах

преобразования

2. Суждение об устойчивости по корням характеристических уравнений.

Характеристическое уравнение в z - изображениях имеет согласно выражению (2.5) вид

D*(z) = 1 - (1 - k) z

-1

1= 0. 1 1 1 1 1 1 (2.8)

Корень этого уравнения z

1= 1 - k по условиям устойчивости должен находиться внутри круга

единичного радиуса, то есть |z

| = |1 - k| < 1 и мы вновь приходим к неравенству (2.7).

3. Использование алгебраического критерия Гурвица.

Вводя подстановку

z =

1 + w

1 - w

в формулу (2.8), получим характеристическое уравнение замкнутой системы в виде

D*(z) = 1 - (1 - k)

1 - w

1 + w

= k + (2 - k)w = 0.

По критерию Гурвица система первого порядка устойчива, если все коэффициенты

характеристического уравнения положительны, то есть k > 0 и 2 - k > 0. Отсюда для устойчивой

системы 0 < k < 2.

4. Использование логарифмического критерия.

Вводя подстановку

z =

1 + w

1 - w

получим выражение для исходной передаточной функции разомкнутой системы

K*(w) =

1 - w

1 + w

1 -

1 - w

1 + w

k(1 - w)

. 1 1 1 1 1 1 (2.9)

Если по аналогии с непрерывными системами, где вводится замена p = jω, подставить в

выражение (2.9) w = jν, то можно построить частотные характеристики разомкнутой дискретной

системы и по ним судить об устойчивости замкнутой системы. Для использования

логарифмического критерия на рис. 2.5 построены ЛЧХ, соответствующие выражению (2.9).

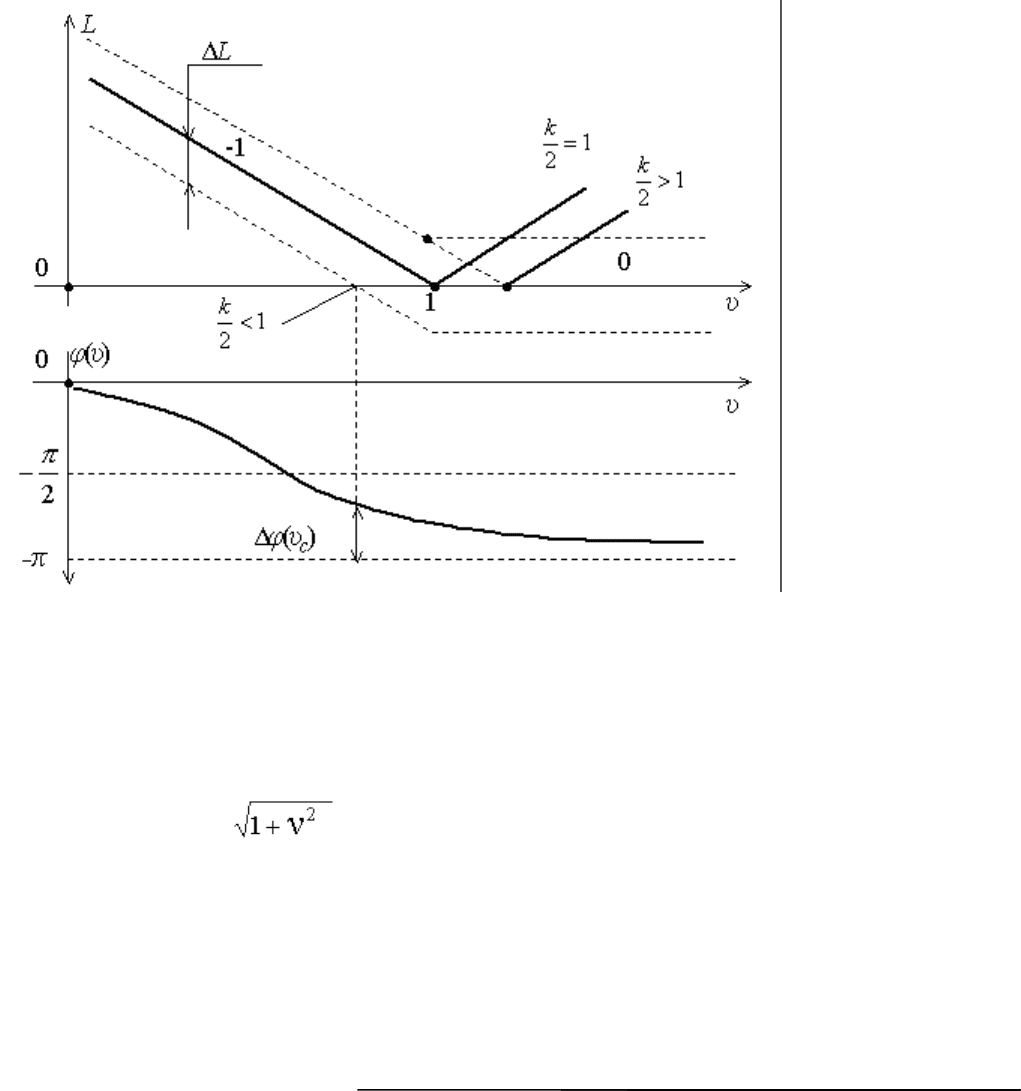
Рис.12.5. Логарифмические характеристики дискретной системы при различных коэффициентах

преобразования

При построении учтено, что k / 2ω - аналог передаточной функции соединения усилительного и

интегрирующего звеньев, а (1 - w) - аналог передаточной функции дифференцирующего звена 1-го

порядка неминимально-фазового типа. У этого звена

L(ν) = 20 lg|1 - w| = 20 lg1 1и ψ(ν) = - arctg(ν);

На рис. 2.5 показаны ЛАХ системы для k < 2, k = 2 и k > 2. Согласно, логарифмическому критерию

замкнутая система будет устойчивой только при k / 2 < 1, так как в любом другом случае частота

среза равна бесконечности и при этом φ(ν

) = - 180° (см. рис. 2.5). Отметим, что рассматриваемая

система теряет устойчивость на половинной частоте квантования. Действительно, согласно

формуле (2.4)

ν = tg

ωT

1 1 и при ν = ∞ 1 1

ωT

Отсюда

ω =

, где Ω =

2 π

Приведенный пример показывает, что все способы оценки устойчивости дают одинаковые

результаты. Выбор способа зависит от сложности системы, исходного материала и необходимого

вида получаемых данных. Для оценки устойчивости с помощью критерия Гурвица в табл. П.3

приведены расчетные соотношения, связывающие условия устойчивости дискретных систем с

коэффициентами характеристического уравнения

D*(z) = 0 при n = 1, ... , 4.

Степень устойчивости в дискретных системах, как и в теории непрерывных систем, оценивается

по степени удаления корней характеристического уравнения D*(z) = 0 от линии круга единичного

радиуса (рис. 2.2). Косвенной оценкой степени устойчивости и здесь служат запасы устойчивости

по фазе Δφ(ν

) и амплитуде ΔL (см., например, рис. 2.5). Отметим одну особенность, характерную

только для дискретных систем. Пусть передаточная функция системы описывается соотношением

(z) =

1+ b

-1

1+ ... + b

-m

1+ c

-1

1+ ... + c

-n

P*(z)

D*(z)

. 1 1 1 1 1 1 (2.10)

В отличие от непрерывных систем в дискретных можно (по крайней мере, в принципе) подобрать

параметры системы так, чтобы все коэффициенты c

1характеристического уравнения D*(z) = 0

кроме с

, равнялись нулю. В этом случае (2.10) примет вид

(z) =

P*(z)

, 1 1 1 1 1 1 (2.11)

что соответствует нахождению всех корней характеристического уравнения D*(z) = 0 в центре

единичного круга. Если выполняется условие (2.11), то говорят, что линейная дискретная система

имеет бесконечную степень устойчивости. Ниже будет показано, что в таких системах переходный

процесс заканчивается за конечное и минимально возможное число периодов Т

. Здесь же

отметим, что для примера 2.1 условие (2.7) выполняется при k = 1, когда коэффициент c

1при z

1полинома знаменателя передаточной функции (2.5) становится равным нулю.

2.2. Качество дискретных систем в переходном режиме

Как и в теории непрерывных систем, качество дискретных в переходном режиме оценивается

прямыми и косвенными показателями, причем первые из них принято отождествлять с

показателями переходной характеристики, а вторыми могут служить дискретные аналоги

интегральных оценок - суммарные оценки.

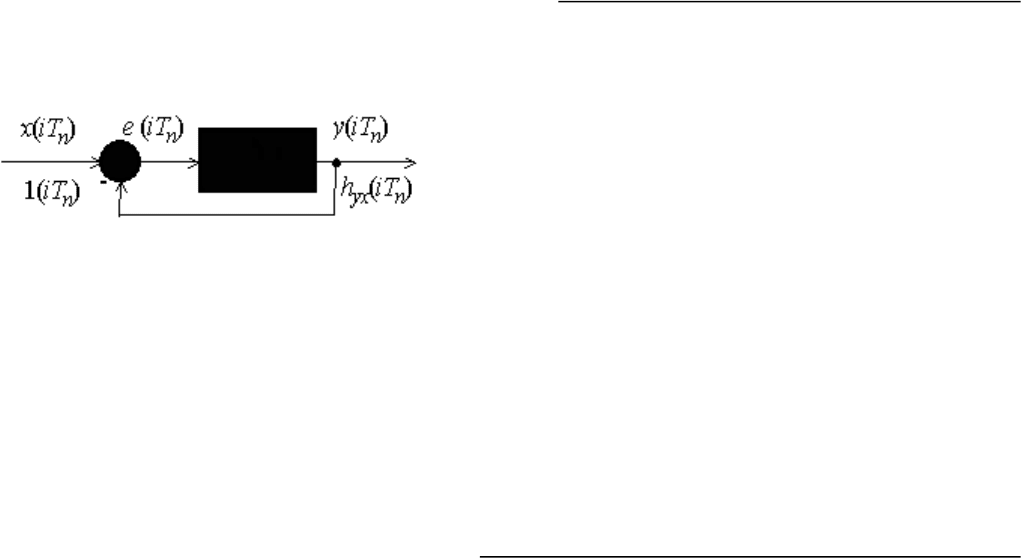
Переходная характеристика замкнутой системы h

(iT

) определяется как реакция этой системы на

дискретную единичную функцию (рис. 2.6)

x(iT

) = 1(iT

) или x*(z) =

1 - z

-1

Рис.12.6. Структурная схема дискретной системы

Она может быть вычислена непосредственно по разностному уравнению

(iT

) + c

[(i-1)T

] + ... + c

[(i-n)T

] =1

= b

11(iT

) + ... + b

11[(i-m)T

] 1 1 1 1 1 1 (2.12)

при нулевых начальных условиях или с помощью любого из приемов определения обратного z-

преобразования от изображения

(z) = x*(z) K

(z) =

(z)

1 - z

-1

. 1 1 1 1 1 1 (2.13)

Пример 2.2.

Вычислим для условий примера 2.1 переходную характеристику, воспользовавшись двумя

указанными способами.

1. Разностное уравнение в z-изображениях для переходной характеристики записывается из

выражения (2.6)

(z) - (1 - k) z

-1

(z) = k z

-1

1x*(z)

или в оригиналах при x(iT

) = 1(iT

)

(iT

) = k 1[(i - 1)T

] + (1 - k) h

[(i - 1)T

]. 1 1 1 1 1 1 (2.14)

Вычисленные с помощью формулы (2.14) переходные характеристики h

(iT

) для различных

коэффициентов преобразования системы k представлены на рис. 2.7. При решении уравнения

(2.14) учтено, что 1(iT

) = 0 при i < 0.

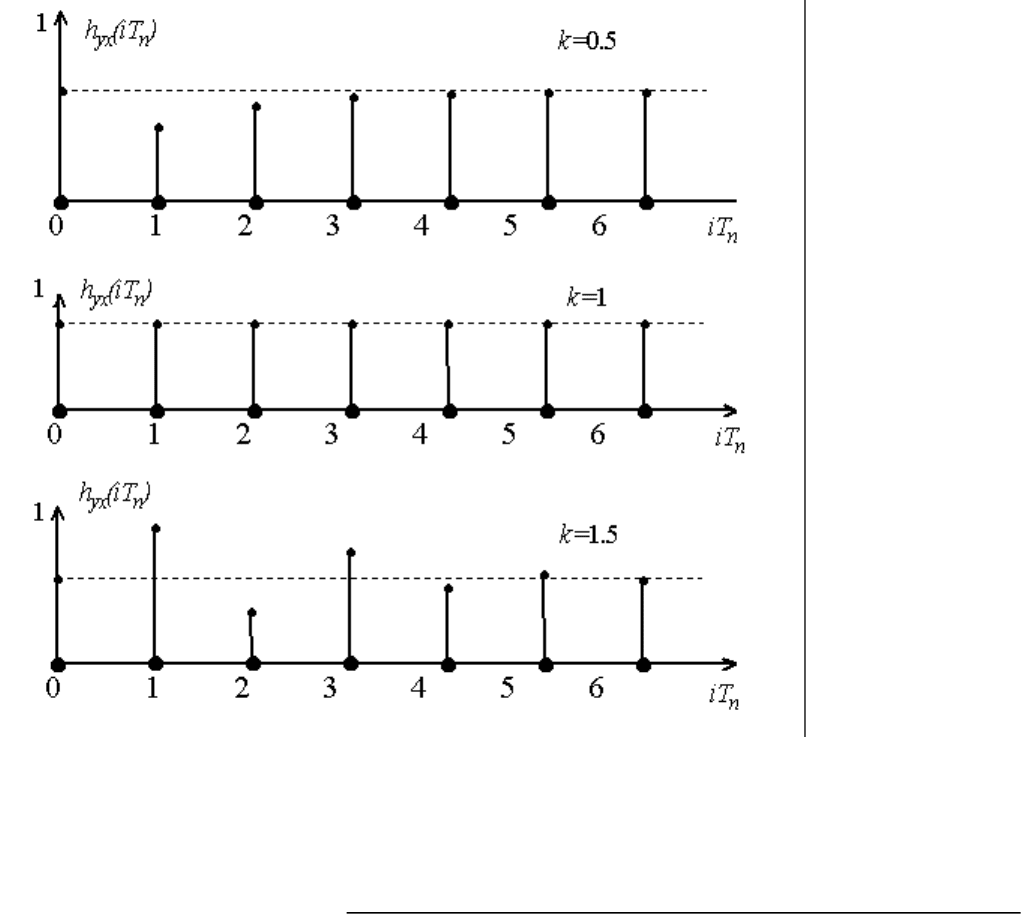
Рис.12.7. Переходные характеристики дискретной системы при К=0.5 (а); К=1 (б); К=1.5 (в)

2. z-изображение переходной характеристики согласно формулам (2.13) и (2.5) равно

(z) =

k z

-1

(1 - z

-1

)[1 - (1 - k) z

-1

]

. 1 1 1 1 1 1 (2.15)

С другой стороны, по определению

(z) =

∞

i = 0

(iT

) z

-1

и, следовательно, можно записать

k z

-1

1= (1 - z

-1

)[1 - (1 - k)z

-1

][h

(0) + h

) z

-1

1+ h

(2T

) z

-2

1+ ...].

Сравнивая коэффициенты при одинаковых степенях z в левой и правой частях равенства,

нетрудно получить значения h

(iT

), совпадающие с результатом решения уравнения (2.15).

В подразделе 2.1 отмечалось, что при выполнении условий бесконечной степени устойчивости

переходный процесс в системе заканчивается за конечное, вполне определенное число периодов

. Покажем, что это выполняется и для переходной характеристики, учитывая, что указанные

условия имеют место, если все коэффициенты характеристического уравнения замкнутой системы

D*(z) = 0 кроме c

, равны нулю, то есть передаточная функция соответствует выражению (2.11). В

этом случае согласно (2.13)

(z) =

1 - z

-1

1+ b

-1

1+ ... + b

-m

или

1+ f

-1

1+ ... + f

-m

1= (1 - z

-1

)[h

(0) + h

) z

-1

1+ h

(2T

) z

-2

1+ ...],

где принято обозначение

Сравнивая теперь коэффициенты при одинаковых степенях z, можно получить

1= h

(0); f

1= h

) - h

(0);

1= h

(2T

) - h

); ... ; f

1= h

(mT

) - h

[(m - 1)T

];

0 = h

[(m + 1)T

] - h

(mT

) или h

[(m + 1)T

] = h

(mT

Таким образом, при бесконечной степени устойчивости переходная характеристика принимает

установившееся значение за конечное число периодов m (рис. 2.8), количественно равное порядку

полинома числителя передаточной функции системы. Так, в рассмотренном примере, условие

бесконечной степени устойчивости k = 1 [см. формулу (2.5)], при этом согласно выражению (2.15)

(z) =

-1

1 - z

-1

и переходная характеристика принимает установившееся значение за один период.

Рис.12.8. Переходная характеристика при бесконечной степени устойчивости

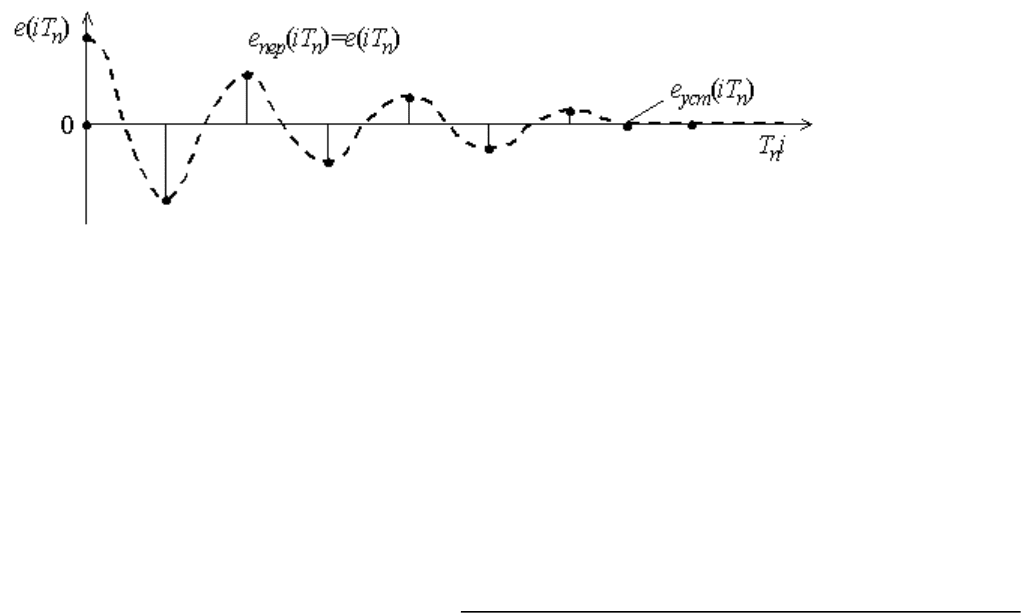
Косвенными оценками, учитывающими как длительность, так и форму процесса в переходном

режиме, могут служить суммарные оценки. Наиболее общей из них является квадратичная

суммарная оценка - аналог интегральной квадратичной оценки в теории непрерывных систем:

Q* =

∞

i = 0

[e(iT

) - e

уст

(iT

)]

∞

i = 0

пер

1(iT

)]; 1 1 1 1 1 1 (2.16)

e(iT

) = x(iT

) - y(iT

где e(iT

) - ошибка, а e

уст

(iT

) и e

пер

(iT

) - ее установившаяся и переходная составляющие (рис. 2.9).

Рассмотрим последовательность вычисления суммарной оценки:

1) находится z-изображение ошибки

e*(z) = x*(z) K

(z),

где K

(z) - передаточная функция ошибки, описываемая для следящих систем формулой (1.32);

Рис.12.9. Ошибки дискретной системы

2) по выражению (1.20) для конечных значений (подраздел 1.4) определяется установившееся

значение ошибки

уст

lim

i → ∞

e(iT

) =

lim

i → ∞

(1 - z

-1

) e*(z)

и его z-изображение e*

уст

(z) = Z{e

уст

};

3) составляется разность e*

пер

(z) = e*(z) - e*

уст

(z) и после подстановки в нее

z =

1 + w

1 - w

записывается e*

пер

(w);

4) с помощью таблиц интеграла Парсеваля определяется квадратичная суммарная оценка

Q* = 2I [ e*

пер

(w) ].

1 + w

Отметим, что при вычислении e*

пер

(z) знак разности может получиться как положительным, так и

отрицательным, что при дальнейших вычислениях не принимается во внимание, так как

рассчитывается квадратичная оценка. Отметим также, что в формуле (2.16) вместо ошибки e(iT

)

могут быть использованы выходные y(iT

) или какие-либо другие координаты системы, если их

установившиеся значения легко вычисляются.

Пример 2.3.

Определить квадратичную суммарную оценку качества переходного режима в системе для

условий примера 2.1, полагая, что на вход замкнутой системы (рис. 1.16) подаются:

1) дискретная единичная функция x(iT

) = x

11(iT

) или

x*(z) =

1 - z

-1

;

2) дискретная линейная функция x(iT

) = x

1iT

1или

x*(z) =

-1

(1 - z

-1

)

;

Здесь z-изображения записаны на основании табл. П.2. для огибающих x(t) = x

1(t) и x(t) = x

t. В

рассматриваемом примере

K*(z) =

k z

-1

1 - z

-1

P*(z)

Q*(z)

и, следовательно, передаточная функция ошибки

(z) =

Q*(z)

D*(z)

1 - z

-1

1 + z

-1

(k - 1)

z-изображение ошибки в случае дискретной единичной функции

e*(z) = x

= 1 - z

-1

= x