Грамагин Е.А. Теория дискретных систем управления
Подождите немного. Документ загружается.


C
0
C
0
Взяв i = 2, находим значение на втором шаге
y(2T
n
) =
1
C
0
{b
0
1x(2T
n
) - C
1
1y(T
n
) - C
2
1y(0)] =
=
1
1
C
0
{b
0
12T
n
1- C
1
b
0
C
0
T
n
) =
b
0
C
0
(
1
12 -
C
1
C
0
) T
n
.
По такой же схеме можно последовательно вычислять значения выходной переменной и в другие
моменты времени.
1.4. Дискретное преобразование Лапласа
Одним из наиболее распространенных методов анализа линейных дискретных систем является
операторный метод, основанный на дискретном преобразовании Лапласа, которое по своим
возможностям и методике применения близко к преобразованию Лапласа для непрерывных
функций.
Дискретным преобразованием Лапласа (ДПЛ) от функции х(iT
n
) называется сумма
x*(p) =
∞
Σ
i = 0
x(iT
n
) e
-piTn
1= D[x(iT
n
)], 1 1 1 1 1 1 (1.10)
где р - комплексная переменная. Легко увидеть аналогию между этим соотношением и
непрерывным преобразованием Лапласа L[x(t)]. Верхний индекс в виде звездочки у изображения
х*(р) поставлен, чтобы отличать его от изображения непрерывной функции х(р).
Рассмотрим основные свойства дискретного преобразования Лапласа, которые будут
использоваться при дальнейшем изложении.
а) ДПЛ обладает свойством периодичности, заключающемся в том, что
х*(р) = x*(p + jkΩ), 1 1 1 1 1 1 (1.11)
где Ω = 2π / T
n
1- частота квантования, k - любое целое число (нуль, положительное или
отрицательное). Докажем это свойство, для чего согласно (1.10) запишем сумму
x*(p + jkΩ) =
∞
Σ
i = 0
x(iT
n
) e
-(p + jkΩ)iTn
1=
∞
Σ
i = 0
x(iT
n
) e
-pTn
1e
-jki Ω Tn
11
Так как ΩT
n
1= 2π, то сомножитель
e
-jki Ω Tn
1= e
-j 2ki π
1= e
-j 2 π
1= 1
поскольку произведение целых чисел ki, в свою очередь, дает целое число. Таким образом,
получаем
x*(p + jkΩ) =
∞
Σ
i = 0
x(iT
n
) e
-piTn
1= x*(p),
что и требовалось доказать.
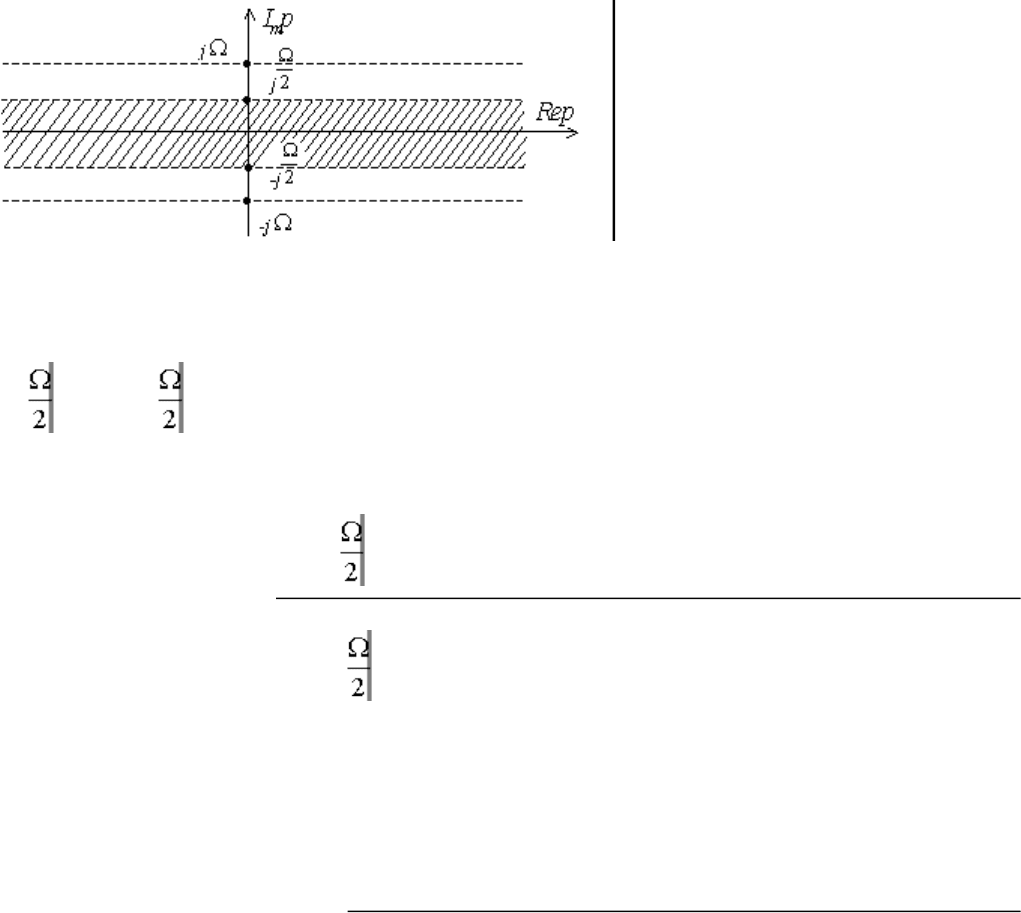
Свойство периодичности говорит о том, что функция х*(р) располагается на комплексной
плоскости р периодически относительно мнимой оси Im p с периодом jΩ (рис. 1.8).
Рис.11.8. Главная полоса комплексной плоскости
Для изучения функции х*(р) достаточно рассматривать лишь главную полосу в пределах
- j1 1≤ Im p ≤ j1
(рис. 1.8), поэтому обратное дискретное преобразование Лапласа
x(iT
n
) =
T
n
2 π j
j1
∫
-j1
x*(p) e
piTn
1dp = D
-1
[x*(p)] 1 1 1 1 1 1 (1.12)
имеет область интегрирования только в пределах главной полосы.
б) Связь между изображением х*(р) дискретной функции и изображением х(р) непрерывной
огибающей имеет вид
x*(p) = 1 ∞
Σ
k = -∞
x(p - jkΩ). 1 1 1 1 1 1 (1.13)
12

T
n
Докажем это соотношение, для чего предварительно рассмотрим некоторые свойства бесконечной
периодической последовательности дельта-функций, следующих с периодом T
n
Δ(t) =
∞
Σ
i = -∞
δ(t - iT
n
).
Как и всякую периодическую функцию ее можно разложить в ряд Фурье и представить в виде
бесконечной суммы гармонических составляющих
Δ(t) =
∞
Σ
k = -∞
c
k
1e
jk Ω t
, 1 1 1 1 1 1 (1.14)
где комплексная амплитуда k-й гармоники
c
k
1=
1
T
n
T
n
2
∫
-T
n
2
Δ(t) e
jk Ω t
1dt =
1
T
n
T
n
2
∫
-T
n
2
∞
Σ
i = -∞
δ(t - iT
n
) e
jk Ω t
1dt.
Так как интегрирование ведется в пределах
-
T
n
2
≤ t ≤
T
n
2
,
то из всей последовательности дельта-функций в этот предел попадает лишь центральное
слагаемое при i = 0, а поэтому
c
k
1= 1 T
n
δ(t - iT
n
) e
jk Ω t
1dt = 1 .
13

T
n
2
∫
-T
n
2
T
n
Подставляя это равенство в формулу (1.14), получаем ряд Фурье в виде
Δ (t) =
1
T
n
∞
Σ
k = -∞
e
jk Ω t
.
Теперь найдем, чему равен интеграл от произведения функций:
∞
∫
0
Δ (t) e
-pt
1dt =
∞
∫
0
∞
Σ
i = -∞
δ(t - iT
n
) x(t) e
-pt
1dt =
=
∞
Σ
i = 0
∞
∫
0
δ(t - iT
n
) x(t) e
-pt
1dt =
∞
Σ
i = -∞
x(iT
n
) e
-piTn
1= x*(p). 1 1 1 1 1 1 (1.15)
Здесь при замене местами суммирования и интегрирования нижний предел суммирования принят
равным нулю, так как функция x(t) берется в пределах от нуля до бесконечности. Выражение
(1.15) дает связь между изображением дискретной функции х*(р) и непрерывной огибающей x(t).
Подставим в это выражение вместо Δ (t) ее разложение в виде ряда Фурье и получим
x*(p) =
∞
∫
0
Δ(t) x(t) e
-pt
1dt =
∞
∫
0
1
T
n
∞
Σ
k = -∞
e
jk Ω t
1x(t) e
-pt
1dt =
=
1
T
n
∞
Σ
k = -∞
∞
∫
0
x(t) e
- (p - jk Ω) t
1dt.
Внутренний интеграл является преобразованием Лапласа от x(t) с комплексной переменной р -
jkΩ, что приводит к формуле (1.13).
Для практического использования ДПЛ удобно ввести новую ком-плексную переменную z = e
pTn
.
Получающееся при этом выражение
х*(z) =
∞
Σ
i = 0
x(iT
n
) z
-1
1= Z[x(iT
n
)] 1 1 1 1 1 1 (1.16)
14

называется z - преобразованием. Рассмотрим соответствующее ему обратное преобразование,
для чего в формуле (1.12) введем новые обозначения:
e
-piTn
1= z
i
; dz = T
n
1e
pTn
1dp; dp =
1
T
n
z
-1
1dz.
Так как комплексная переменная p меняется в пределах
- j
Ω
2
≤ p ≤ j
Ω
2
,
то новая переменная z будет находиться в диапазоне
e
- j Ω
2
≤ z ≤ e
j Ω
2
.
В этих пределах модуль |z| = 1, а аргумент
- π ≤ arg z ≤ π,
поэтому интегрирование в плоскости z будет идти вдоль окружности единичного радиуса. После
всех подстановок получим формулу обратного z-преобразования
x(iT
n
) =
1
2 π j
|x|=1
x*(z) z
i-1
1dz,
где символически обозначен путь интегрирования вдоль окружности еди-ничного радиуса.
Продолжим изучение свойств ДПЛ уже в форме z-преобразования.
в) Изображение функции х[(i- k)T
n
] с запаздывающим аргументом kT
n
1равно
Z{x[(i- k)T
n
]} = z
-k
x*(z). 1 1 1 1 1 1 (1.17)
Для доказательства запишем z-преобразование от рассматриваемой функции
∞
Σ
i = 0
x[(i-k)T
n
]z
-i
1=
∞
Σ
r = -k
x(rT
n
) z
-(r+k)
,
где использована замена переменной i-k = r или i = r+k. С учетом того, что функция x(iT
n
)
рассматривается только при положительном времени iT
n
, нижний предел суммирования можно
заменить нулем и записать
15
∞
Σ
r = -k
x(rT
n
) z
-(r+k)
1= z
-k
∞
Σ
r = 0
x(rT
n
) z
-r
1= z
-k
1x*(z),
что и доказывает соотношение (1.17).
г) Изображение разности k-ro порядка равно
Z[Δ
k
1x(iT
n
)] = (1-z
-1
)
k
1x*(z). 1 1 1 1 1 1 (1.18)
Докажем это равенство. Используя формулу (1), запишем изображение первой разности
Z[Δ
1
1x(iT
n
)] = Z{x(iT
n
) - x[(i-1)T
n
]} = x*(z) - z
1-1
1x*(z) = (1 - z
1-1
)
k
1x*(z).
Из формулы (1.2) для второй разности получаем
Z[Δ
2
1x(iT
n
)] = Z{x(iT
n
) - 2x[(i-1)T
n
] + x[(i-2)T
n
]} =
= x*(z)- 2z
1-1
x*(z) + z
1-2
x*(z) = (1-z
1-1
)
k
1x*(z).
Проделав такую же операцию над третьей разностью (1.3), можно по индукции убедиться в
справедливости общего соотношения (1.18).
д) Следующее интересующее нас свойство говорит о том, что изображение x*(z) является
рациональной функцией переменной z
1-1
, то есть может быть представлено в виде отношения
полиномов
x*(z) =
a
0
1+ a
1
z
1-1
1+ a
2
z
1-2
1+ ... + a
m
z
1-m
β
0
1+ β
1
z
1-1
1+ β
2
z
1-2
1+ ... + β
n
z
1-n
1 1 1 1 1 1 (1.19)
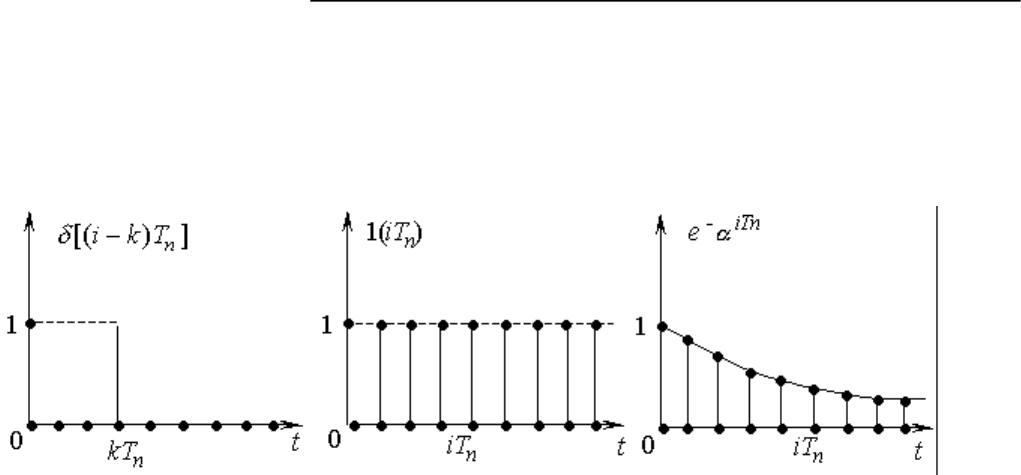
Убедимся в этом на нескольких конкретных примерах. В простейшем случае дискретная функция
состоит из одной дискреты единичной амплитуды, расположенной в момент времени t = kT
n
1(рис.
1.9, а).
Рис.11.9. Примеры дискретных функций
Такую функцию будем называть единичным дискретным импульсом со следующими свойствами:
δ [(i-k)T
n
] = { 1 при i = k
0 при i ≠ k
16

Найдем изображение этой функции, пользуясь формулой (1.16):
Z{δ[(i-k)T
n
]} =
∞
Σ
i = 0
δ[(i-k)T
n
] z
-i
1= z
-k
.
Если единичный дискретный импульс расположен в начале координат (k = 0), то его изображение
x*(z) = 1.
Теперь положим, что непрерывная огибающая является единичной функцией
x(t) = 1(t).
Тогда соответствующая ей функция х(iТ
n
) называется единичной дискретной функцией (рис. 1.9,
б) и равна
1 (iT
n
) = {
1 при i = 0, 1, 2, ... ;
0 при i < 0.
Изображение единичной дискретной функции
Z[1(iT
n
)] =
∞
Σ
i = 0
z
-i
1= 1 + z
-1
+ z
-2
1+ ... =
1
1 - z
-1
где учтено значение суммы бесконечной геометрической прогрессии
∞
Σ
i = 0
q
i
1= 1 + q + q
2
1+ ... =
1
1 - q
В заключение найдем изображение дискретной экспоненциальной функции
x(iT
n
) = e
1-aiTn
(рис. 1.9, в). Из формулы (1.16) следует, что
Z[e
-aiTn
] =
∞
Σ
i = 0
e
-aiTn
1z
-i
1= 1 + e
-aTn
1z
-1
1+ e
-2aTn
1z
-2
1+ ... =
1
1 - e
-aTn
1z
-1
где также учтена сумма бесконечной геометрической прогрессии. Изображения для некоторых
других дискретных функций приводятся в табл. П. 2. Полученные результаты и данные таблицы
подтверждают правильность вывода о рациональном характере функции x*(z).
17

Запись изображения в виде (1.19) позволяет рекуррентным способом вычислять значения
оригинала х(iT
n
) по изображению х*(z). Для этого перепишем выражение (1.19) в другом виде
a
0
1+ a
1
z
1-1
1+ a
2
z
1-2
1+ ... + a
m
z
1-m
1=1
(β
0
1+ β
1
z
1-1
1+ β
2
z
1-2
1+ ... + β
n
z
1-n
) [x(0)+ x(1T
n
)z
1-1
+ x(2T
n
)z
1-2
1+ ...]
Приравнивая коэффициенты в левых и правых частях равенства при одинаковых степенях z
1-k
1(k =
0, 1, 2,…), получим соотношения для искомой функции x(iT
n
) при i = 0, 1, 2 ... . Проделаем это для
нескольких первых членов:
a
0
1= β
0
1x(0); x(0) =
a
0
β
0
;
a
1
1= β
0
1x(T
n
) + β
1
1x(0); x(T
n
) =
1
β
0
[a
1
1- β
1
1x(0)];
a
2
1= β
0
1x(2T
n
) + β
1
x(T
n
) + β
2
1x(0); x(2T
n
) =
1
β
0
[a
2
1- β
1
1x(T
n
) - β
2
1x(0)].
По индукции можно получить следующую формулу для значения процесса в произвольный
момент iT
n
x(iT
n
) =
1
β
0
{a
i
1-
i
Σ
k = 1
β
k
1x[(i-k)T
n
]}.
Особенность этого выражения состоит в последовательном (рекуррентном) вычислении
переменных, начиная с первого периода следования.
е) Установившееся значение дискретной функции определяется по формуле
lim
i → ∞
x(iT
n
) =
lim
z → 1
(1- z
-1
) x*(z). 1 1 1 1 1 1 (1.20)
18
Изображение дискретной функции можно представить в виде предела
х*(z) =
lim
k → ∞
k
Σ
i = 1
x(iT
n
) z
-i
,
а функции с запаздыванием на один период
z
-1
1х*(z) =
lim
k → ∞
k
Σ
i = 1
x[(i-1)T
n
] z
-i
,
где учитывается равенство x(iT
n
) = 0 при i < 0.
Тогда при z → 1 можно записать следующее равенство:
lim
z → 1
[x*(z)- z
-1
1x*(z)] =
lim
z → 1
(1- z
-1
) x*(z) =
lim
k → ∞
{x(0) + x(iT
n
) +
+ x(2T
n
) + ... + x(kT
n
) - x(0) - x(T
n
) -
- x(2T
n
) - ... - x[(k-1)T
n
]} =
lim
k → ∞
x(kT
n
),
которое и доказывает свойство ( 1.20).
Z-преобразование является основным математическим аппаратом ис-следования линейных
стационарных дискретных систем и поэтому широко используется в дальнейшем изложении.
1.5. Частотный спектр дискретного процесса
Заменяя в формуле (1.10) дискретного преобразования Лапласа переменную р на jω, получаем
дискретное преобразование Фурье
x*(jω) =
k
Σ
i = 0
x(iT
n
) e
-jω Tn i
,
которое определяет частотный спектр дискретного процесса. Чтобы получить спектр из формулы
z-преобразования ( 1.16), надо ввести замену переменной
z = e
jω Tn
Изучим структуру спектра дискретного процесса, для чего воспользуемся формулой связи (1.13)
между изображением х*(р) дискретной функции и ее огибающей. Произведя замену переменной р
на jω, находим спектр дискретного процесса в виде
x*(jω) = 1 ∞
Σ
x[j(ω - kΩ)]. 1 1 1 1 1 1 (1.21)
19

T
n
k = -∞
Таким образом, спектр дискретного процесса является периодической функцией частоты с
периодом
Ω =
2 π
T
n
,
составляющие которой пропорциональны спектру непрерывной огибающей с масштабом 1/T
n
.
Покажем на графиках характер амплитудно-частотного спектра дискретного процесса |x*(jω)| для
следующих двух случаев.
Пусть амплитудный спектр огибающей |x*(jω)| имеет форму, изображенную на верхнем рис. 1.10,
а, где ω
гр
1- граничная составляющая спектра, опре-деляющая его ширину. В первом случае
положим, что
ω
гр
1<
Ω
2
,
и тогда в соответствии с формулой (1.21) спектр дискретного процесса примет вид, изображенный
на нижнем рис. 1.10, а, и характерный наличием отдельных составляющих, совпадающих по
форме с |x*(jω)|. Такая форма спектра называется гребенчатой. Во втором случае положим, что
ω
гр
1>
Ω
2
,
и тогда спектр примет вид, показанный на рис. 1.10, б, где составляющие спектра перекрываются.
По теореме Котельникова, о которой говорилось выше, для восстановления огибающей по
дискретным данным о ней требуется выполнение условия
ω
гр
1<
Ω
2
,
что соответствует спектру на рис. 1.10, а.
20
