Грамагин Е.А. Теория дискретных систем управления

Подождите немного. Документ загружается.

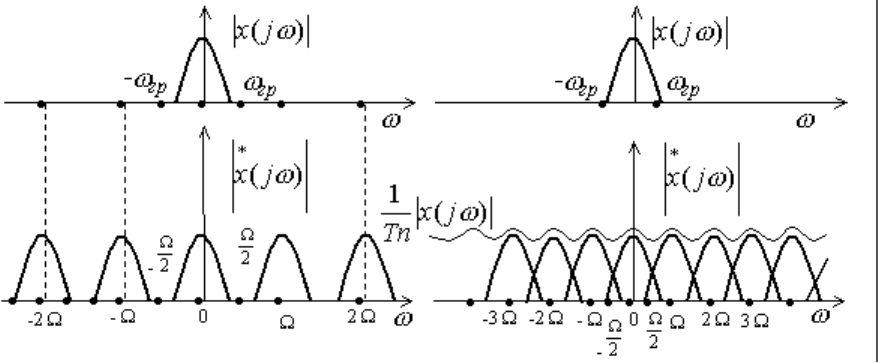
Рис.11.10. Частотный спектр дискретного процесса

Таким образом, частота квантования Ω полезного сигнала должна выбираться так, чтобы спектр

дискретного процесса был гребенчатым. Такому же условию должен удовлетворять и спектр

выходного процесса у*(jω), что накладывает определенные требования на выбор структуры и

параметров дискретной системы. Эти требования рассматриваются ниже.

1.6. Динамические характеристики

К динамическим характеристикам дискретных систем, как и в теории непрерывных систем,

относят передаточные функции, временные (импульсные, переходные) и частотные

характеристики. В литературе принято называть эти характеристики, добавляя слово "дискретная"

(например, "дискретная передаточная функция" - ДПФ, "дискретная переходная характеристика" -

ДПХ и т. д.). Здесь мы ограничимся написанием символа * и аргумента iT

, подчеркивающих

принадлежность характеристик дискретным системам. Перейдем к их рассмотрению, для чего

запишем конечно-разностное уравнение системы

(iT

) +

1y(iT

) + ... +

1y(iT

) =

x(iT

) +

1x(iT

) + ... +

1x(iT

Возьмем z-преобразование от обеих его частей с учетом правила нахождения изображения

конечной разности. В итоге получим операторное уравнение

y*(z)

1- z

-1

) y*(z) + ... +

1- z

-1

)

1y*(z) =

x*(z)

1- z

-1

) x*(z) + ... +

1- z

-1

)

1x*(z),

из которого находим передаточную функцию дискретной системы в виде отношения изображений

(z) =

y*(z)

1- z

-1

) + ... +

1- z

-1

)

P*(z)

. 1 1 1 1 1 1 (1.22)

x*(z)

1- z

-1

) + ... +

1- z

-1

)

D*(z)

По своей структуре эта функция совпадает с передаточной функцией непрерывной системы, если

вместо оператора р подставить оператор (1-z

-1

). Когда разностное уравнение задано в

рекуррентной форме

1y(iT

) + c

1y[(i-1)T

] + ... + c

1y[(i-n)T

] =

= b

1x(iT

) + b

1x[(i-1)T

] + ... + b

1x[(i-m)T

ему будет соответствовать операторное уравнение

1y*(z) + c

-1

1y*(z) + ... + c

-n

1y*(z) =

= b

1x*(z) + b

-1

1x*(z) + ... + b

-m

1x*(z).

После преобразований получим вторую форму записи передаточной функции

(z) =

y*(z)

x*(z)

1+ b

-1

1+ ... + b

-m

1+ c

-1

1+ ... + c

-n

P*(z)

D*(z)

. 1 1 1 1 1 1 (1.23)

Формулы (1.22) и (1.23) эквивалентны и могут быть получены друг из друга. С их помощью

изображение выходного процесса по изображению входного процесса находится как произведение

y*(z) = x*(z)K

(z). 1 1 1 1 1 1 (1.24)

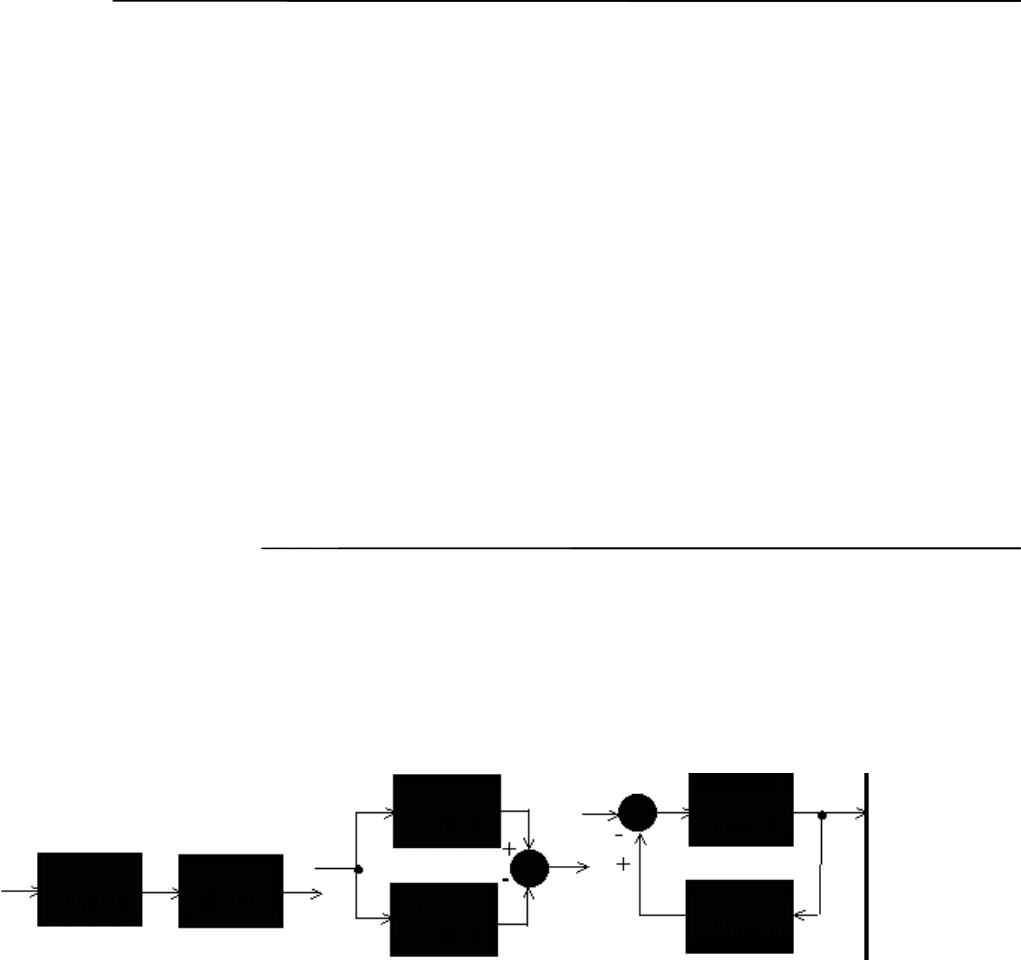
Рис.11.11. Соединение дискретных звеньев

Благодаря одинаковой структуре передаточной функции дискретной системы и передаточной

функции непрерывной системы остаются справедливыми все правила структурных

преобразований, применяемые для непрерывных систем. Так, для последовательного соединения

дискретных звеньев (рис. 1.11,а)

(z) = K

(z) K

(z)

Для параллельного соединения (рис. 1.11,б)

(z) = K

(z) ± K

(z)

Для соединения с обратной связью (рис. 1.11, в)

(z) =

(z)

1 ± K

(z) K

(z)

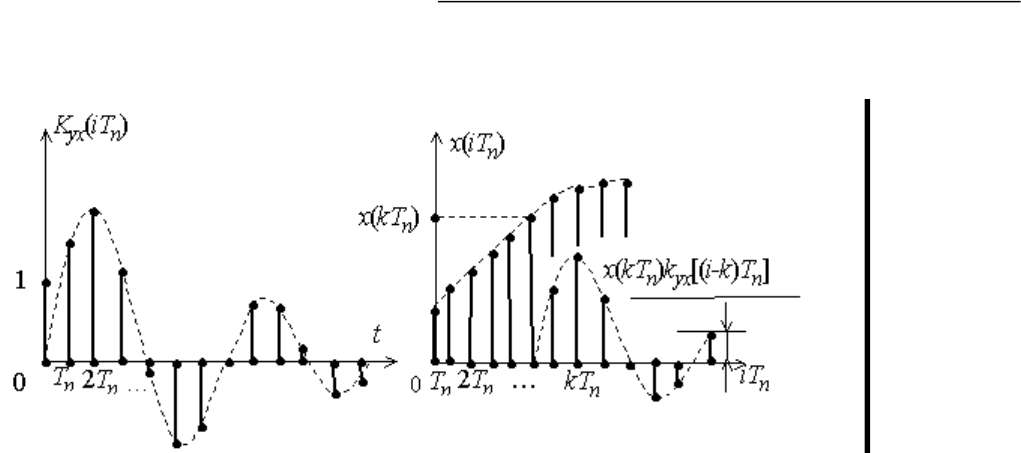
Рис.11.12. Импульсная характеристика дискретной системы

При нахождении временных характеристик в качестве типовых воздействий используются

единичный дискретный импульс и единичная дискретная функция. Импульсной характеристикой

линейной дискретной системы K

(iT

) (рис. 1.12, а) называется реакция на единичный дискретный

импульс δ(iT

) при нулевых начальных условиях. С ее помощью можно определить реакцию

системы на произвольное воздействие х(iT

). Рассматривая рис. 1.12,б, нетрудно понять, что

значение выходного процесса y(iT

) можно подсчитать по формуле

y(iT

) =

∞

k = 0

x(kT

) k

1[(i-k)T

Если учесть условие физической реализуемости импульсной характеристики

[(i-k)T

] = 0

при i < k, то эту формулу можно переписать, заменив верхний предел суммы бесконечностью, то

есть

y(iT

) =

∞

k = 0

x(kT

) k

1[(i-k)T

]; 1 1 1 1 1 1 (1.25)

[(i-k)T

] = 0 при i < k.

Это соотношение называется формулой свертки, оно аналогично интегралу свертки в теории

непрерывных систем. Возьмем z - преобразование от формулы свертки (1.19) и найдем

изображение выходного процесса через импульсную характеристику

y*(z) = ∞ ∞ x(kT

) k

1[(i-k)T

] z

-i

1(z

-k

i = 0

k = 0

Мы искусственно домножили слагаемые на единичный множитель в форме

1 = z

-k

Поменяем местами порядок суммирования, произведем перегруппировку сомножителей и

заменим переменную i-k = r, i = k+r, после чего будем иметь

y*(z) =

∞

k = 0

x(kT

) z

-k

∞

i = 0

1[(i-k)T

] z

-(i-k)

∞

k = 0

x(kT

) z

-k

∞

i = 0

1(rT

) z

-r

По условию физической реализуемости k

(rT

) = 0 при r < 0, поэтому нижний предел у

внутренней суммы можно заменить нулем и она не будет зависеть от переменной k, в результате

чего суммы станут независимыми и их можно поменять местами. Заметим, что первая сумма

∞

k = 0

x(kT

) z

-k

1= x*(z),

поэтому изображение выходной переменной станет равным

y*(z) = x*(z)

∞

r = 0

1(rT

) z

-r

Сравнивая это равенство с формулой (1.24), получаем выражение для передаточной функции

через импульсную характеристику в виде

(z) =

∞

i = 0

1(iT

) z

-i

. 1 1 1 1 1 1 (1.26)

Таким образом, передаточная функция дискретной системы является z-преобразованием от

импульсной характеристики.

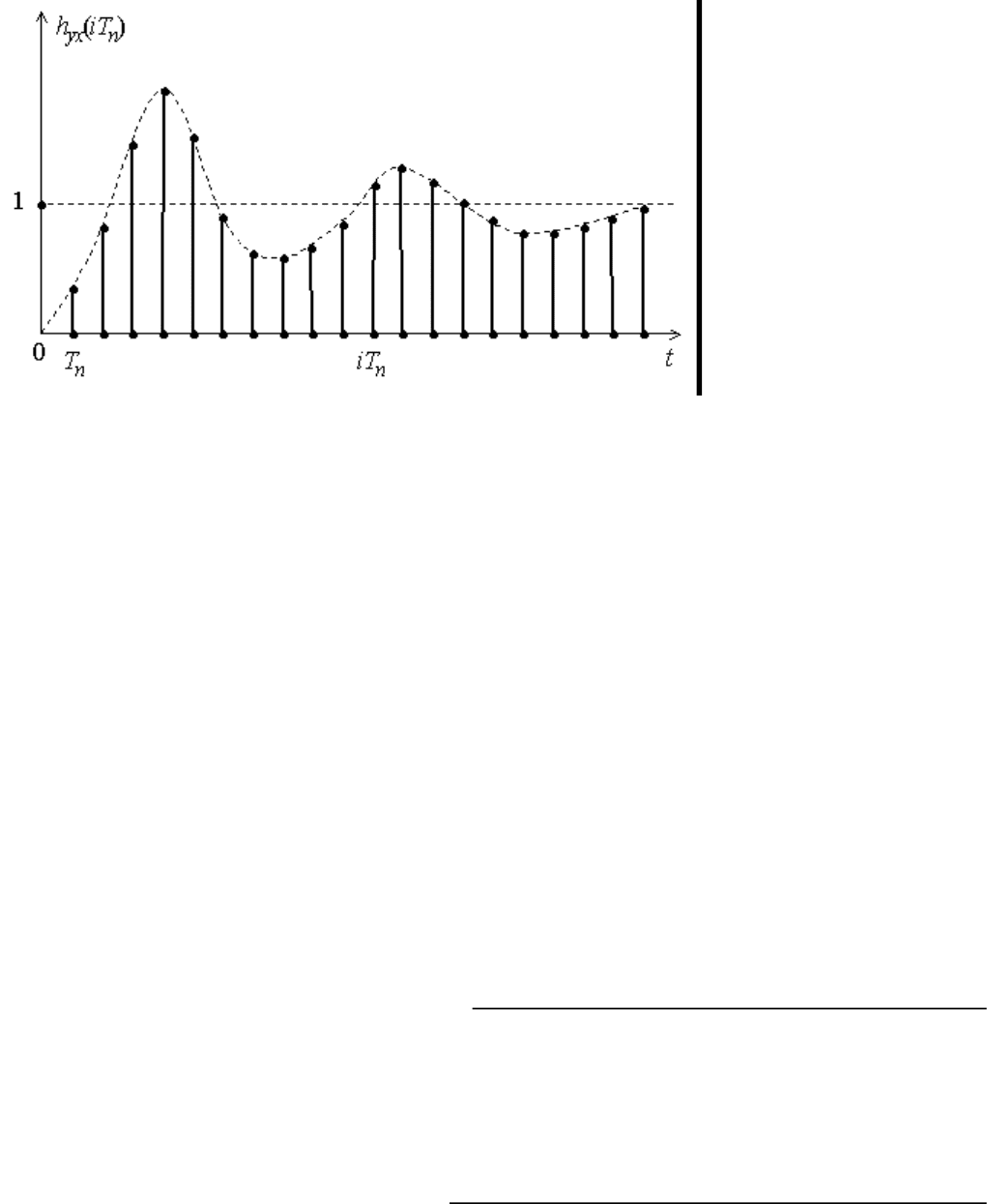
Рис.11.13. Переходная характеристика дискретной системы

Переходной характеристикой линейной дискретной системы h

(iT

) называется реакция на

единичную дискретную функцию 1(iT

) при нулевых начальных условиях (рис. 1.13). Подставляя

в формулу свертки (1.25) функцию

x(iT

) = 1(iT

найдем связь между переходной и импульсной характеристиками в виде

(iT

) =

k = 0

1(kT

) k

1[(i-k)T

] =

k = 0

1[(i-k)T

] =

r = -k

1(rT

) =

r = 0

1(rT

). 1 1 1 1 1 1 ( 1.26)

Переходная характеристика находится в виде суммы значений импульсной характеристики. Так

как изображение единичного воздействия согласно табл. П. 2 равно

Z[1(iT

)] =

1 - z

-1

то изображение переходной характеристики

Z[h

(iT

)] =

1 - z

-1

(z).

Перейдем к рассмотрению частотных характеристик, для чего в передаточной функции K

(z)

заменим переменную

z = е

1j ω Tn

и обозначим полученную функцию через K

(z). Форму частотной характеристики дискретной

системы удобнее всего получить, если вначале рассмотреть непрерывную огибающую k

(t)

импульсной характеристики k

(iT

). На рисунке 1.12, а эта огибающая показана пунктиром.

Возьмем преобразование Лапласа от этой непрерывной функции и назовем ее передаточной

функцией системы по огибающей

(p) =

∞

∫

(t) e

-pt

dt.

Тогда в соответствии с формулой связи (1.13) между изображениями дискретной и непрерывной

функций можно записать, что

(p) =

∞

k = -∞

(p)(p - jkΩ).

Заменяя в этом равенстве p на jω, получаем формулу связи между частотными характеристиками

дискретной системы и частотной характеристикой по огибающей

(jω) =

∞

k = -∞

[j(ω - kΩ)]. 1 1 1 1 1 1 (1.27)

По своему содержанию это выражение аналогично спектру дискретного процесса (1.21).

Рассмотрим амплитудно-частотную характеристику дискретной системы |K

(jω)| в соответствии с

амплитудно-частотной характеристикой по огибающей |K

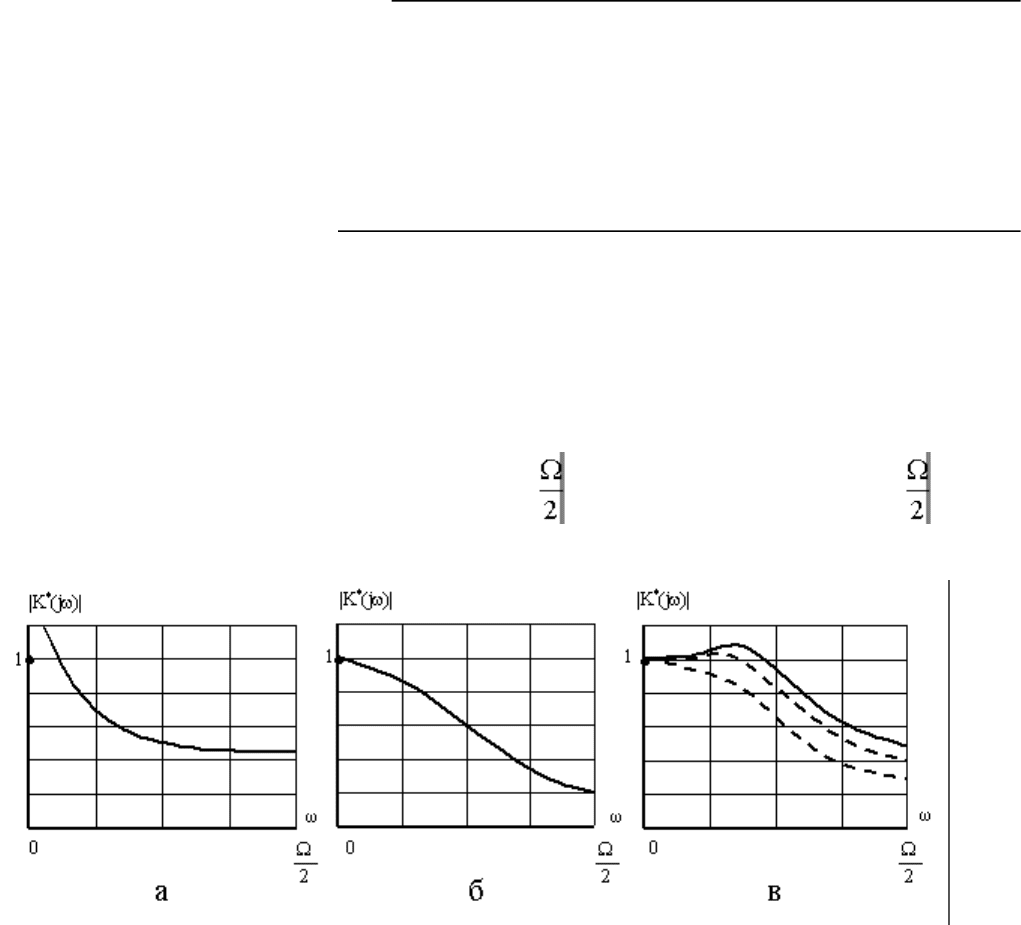
(jω)|. Пусть форма |K

(jω)| имеет вид,

показанный на рис. 1.14, а, где ω

1- полоса пропускания такая, что при ω > ω

1|K

(jω)| → 0.

Частотная характеристика дискретной системы при ω

1<1 1показана на рис. 1.14, а, а при ω

1>1 1

- на рис. 1.14, б.

Рис.11.14. Амплитудно-частотные характеристики инерционных дискретных звеньев

Дискретные системы, у которых ω

1<1 , обладают свойством гребенчатых фильтров. Как будет

показано ниже, эти свойства оказываются необходимыми для качественной работы дискретных

следящих систем.

1.7. Типовые дискретные звенья

Сложную передаточную функцию дискретной системы удобно представлять в виде произведения

передаточных функций типовых звеньев не выше второго порядка, как это делалось для

непрерывных систем. Так как передаточная функция К*(z), записанная формулой (1.23), по своей

структуре аналогична передаточной функции непрерывной системы

(p) =

y(p)

x(p)

1+ b

1p + ... + b

1+ c

1p + ... + c

P(p)

D(p)

где роль р играет разностный оператор (1-z

-1

), то выражения типовых дискретных звеньев

остаются похожими на соответствующие выражения непрерывных. Классификация типовых

дискретных звеньев и некоторые их характеристики даются в табл. П. 4. Аналогия между

дискретными и непрерывными звеньями имеет не только внешний, но и существенный характер.

Особенно наглядно это видно на примере частотных характеристик, которые для дискретных

звеньев получаются заменой

z = e

1jωTn

в передаточной функции К*(z). Особенность этих выражений состоит в том, что параметр τ в них

является безразмерной величиной, поскольку оператор

(1 - z

-1

)

также не имеет размерности. Называть поэтому параметр τ постоянной времени можно лишь

условно. Несмотря на указанное отличие, между типовыми дискретными и непрерывными

звеньями существует глубокая аналогия, которая наглядно видна при сравнении частотных

характеристик. Напомним, что для получения частотной характеристики дискретной системы надо

в передаточной функции К*(z) заменить

z = e

1jωTn

или вместо разностного оператора (1 - z

-1

) взять

(1 - e

1-jωTn

Если ωT

1<< 1, что соответствует низким частотам ω << Ω, то оператор

1 - e

1-jωTn

1→ jωT

а это приводит к практически полному совпадению с частотными характеристиками типовых

непрерывных звеньев с постоянной времени

T = τ T

Таким образом, в области ω, близких к нулю, частотные характеристики дискретных совпадают с

характеристиками соответствующих непрерывных звеньев. Так, например, при ω = 0 частотная

характеристика суммирующего (дискретного интегрирующего) звена равна

K*(jω) = ∞,

а апериодического и колебательного звеньев - единице. С ростом частоты ω от 0 до1 1

амплитудно-частотные характеристики этих звеньев уменьшаются. В дальнейшем они меняются

периодически вдоль оси ω с периодом1 . На рисунке 1.14 показаны АЧХ: а-суммирующего, б-

апериодического, в-колебательного звена при различных значениях параметра ξ. Идеальное

разностное (дискретное дифференцирующее) звено при ω = 0 имеет

K*(jω) = 0,

а разностные первого и второго порядка -1. То же самое имеет место и у соответствующих

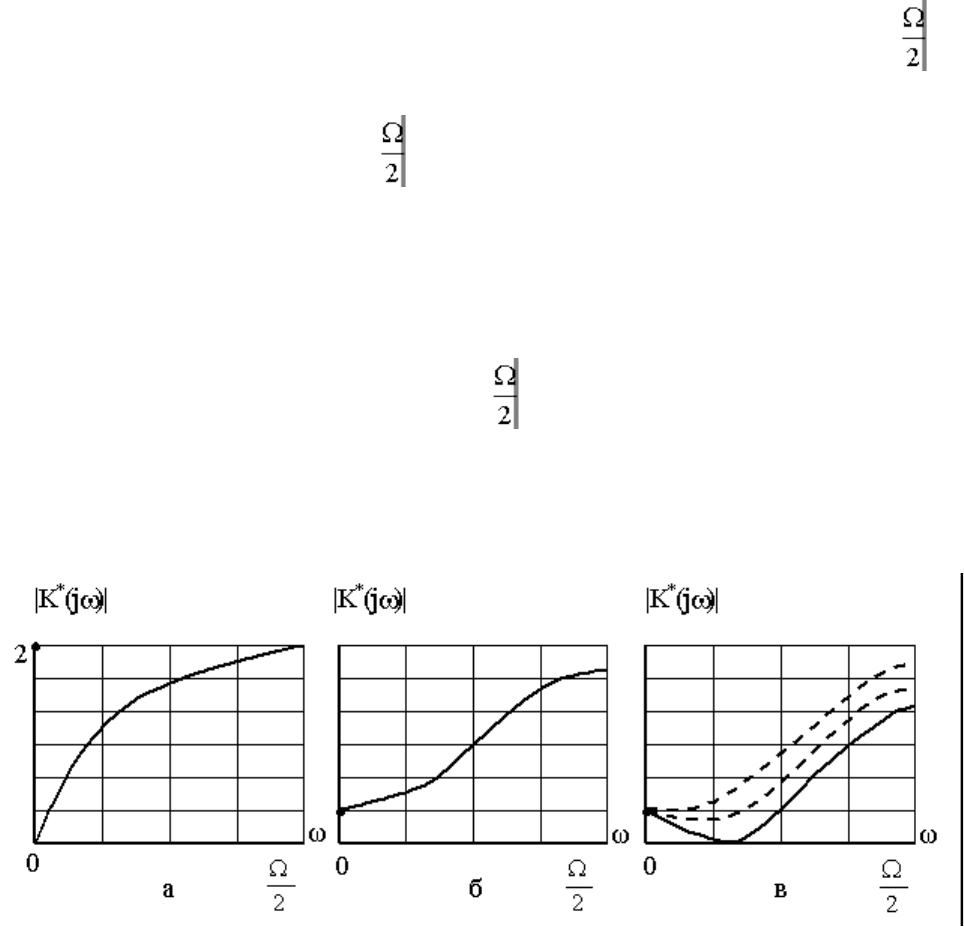
непрерывных звеньев. С ростом частоты ω от 0 до1 1АЧХ разностных звеньев возрастает, что и

показано на рис. 1.15 для идеального разностного звена (а), разностного звена первого порядка (б)

и разностного звена второго порядка (в). Зная характер поведения частотных характеристик

типовых дискретных звеньев, можно судить о желаемой структуре дискретной следящей системы

и, следовательно, о ее желаемой передаточной функции.

Рис.11.15. Амплитудно-частотные характеристики разностных дискретных звеньев

1.8. Частотные характеристики и структурная схема дискретной следящей системы

Дискретная следящая система (рис. 1.16) предназначена для воспроизведения задающего

воздействия х(iТ

), и в идеальном случае выходной процесс в ней должен равняться входному, то

есть

y(iT

) = x(iT

Выполнению этого равенства препятствуют два фактора: наличие возмущающих воздействий и

инерционность системы. Оба эти фактора существенно влияют на выбор формы частотной

характеристики замкнутой системы.

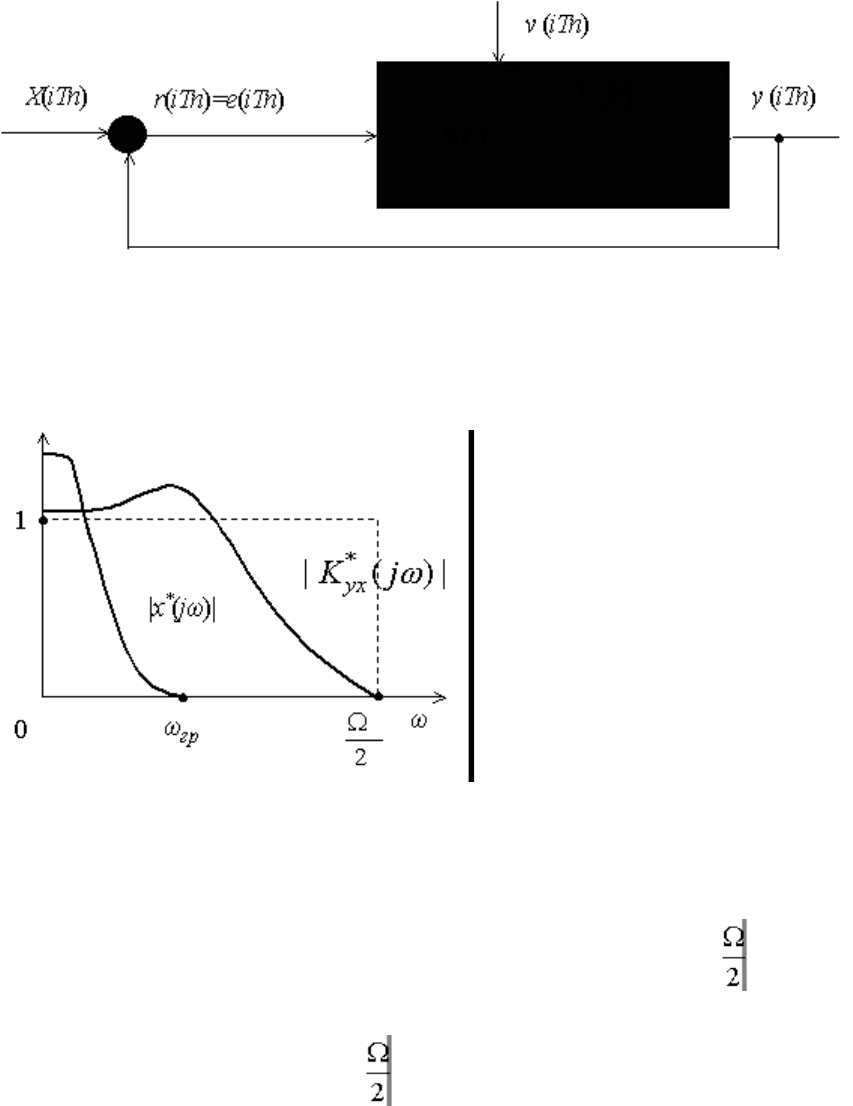
Рис.11.16. Линейная дискретная следящая система

Частотный спектр задающего воздействия х*(jω) расположен в области низких частот и имеет

граничную частоту ω

гр

1( рис. 1.17). В соответствии с теоремой Котельникова, частота квантования

сигнала должна удовлетворять условию Ω > ω

гр

Рис.11.17. Амплитудно-частотная характеристика дискретной следящей системы

Для достаточно полного воспроизведения спектра задающего воздействия на фоне

широкополосных помех частотная характеристика замкнутой следящей системы K

(jω) должна

быть близка к 1 в диапазоне 0 ≤ ω ≤ ω

гр

1и к нулю - в диапазоне ω

гр

1< ω ≤1 . Этому условию, в

частности, удовлетворяет кривая амплитудно-частотной характеристики |K

(jω)| на рис. 1.17.

Стремлению K

(jω) → 0 при ω →1 1соответствуют и условия естественной инерционности

элементов САУ. В итоге, если рассматривать всю область частот, АЧХ замкнутой дискретной

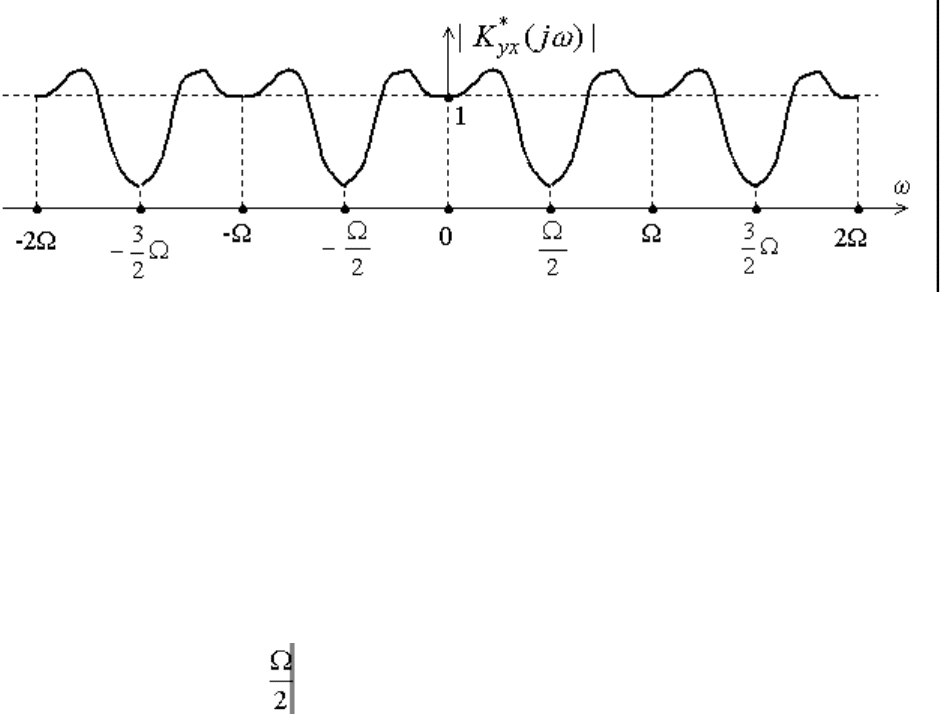
следящей системы должна иметь вид, показанный на рис. 1.18, то есть соответствовать

характеристике гребенчатого фильтра.

Рис.11.18. Амплитудно-частотная характеристика гребенчатого фильтра

Чтобы получить заданную K

(jω), надо сформировать вполне определенную частотную

характеристику разомкнутой системы (рис. 1.16) K

(jω). Очевидно, что требования к последней

аналогичны тем требованиям, которые предъявляются к частотным характеристикам разомкнутых

непрерывных следящих систем. Так, чтобы обеспечить равенство

(jω) ≈ 1

на частотах ω = 0 и ω, кратных Ω (см. рис. 1.18), необходимо иметь K

(jω) → 0, что достигается

включением в состав системы суммирующих (дискретных интегрирующих) звеньев или

усилительных звеньев с очень большим коэффициентом усиления. Чтобы обеспечить условие

(jω) → 0 при ω →1 1в состав разомкнутой системы надо включать инерционные

(апериодические или колебательные) звенья. Согласование хода частотных характеристик в

указанных областях может быть обеспечено разностными (дискретными дифференцирующими)

звеньями.

Анализ частотных характеристик показывает, что структура дискретной следящей системы,

определяемая звеньями, входящими в состав разомкнутой системы, аналогична структуре

непрерывных следящих систем и соответственно аналогичны и передаточные функции

сравниваемых систем. Передаточная функция дискретной разомкнутой следящей системы (рис.

1.16), например, может быть получена из разностного уравнения, записанного в конечно-

разностной форме

y(iT

) +

1y(iT

) + ... +

1y(iT

) =

1 1 1 1 1 1 1 1

r(iT

) +

1r(iT

) + ... +

1r(iT

1 1 1 1 1 1 (1.28)

в виде

K*(z) = =

1- z

-1

) + ... +

1- z

-1

)

= P*(z) . 1 1 1 1 1 1 (1.29)