Graebel W.P. Advanced Fluid Mechanics
Подождите немного. Документ загружается.


144 Exact Solutions of the Navier-Stokes Equations
Use of the orthogonality conditions for the sine gives
A
n
=
b
0
yb −y
2
sin
ny
b
dy
cosh
na
b
b
0
sin
2
ny
b
dy
=
4
b
2
n
3
3
1−−1
n
cosh
na
b
(5.1.9)
The volumetric discharge is given by
Q =
b
0
dy
05b
−05a
u
x
dz =
1
2
p
x
−g cos
×
−ab
3
6
+
n=1
A
n
2b
2
n
2
2
1−−1
n
sinh
na
2b
(5.1.10)
5.1.3 Poiseuille Flow in a Round Conduit or Annulus
For Poiseuille flow in a circular annulus as shown in Figure 5.1.3, adapting the previous
forms to cylindrical polar coordinates suggests letting v =0 0 wr. Again, this form
for the velocity automatically satisfies the incompressible continuity equation. Then
the Navier-Stokes equations in cylindrical polar coordinates (see Appendix) in the z
direction (along the tube) reduces to
p
z
−g cos =
d
2
w
dr
2
+
1
r
dw
dr
Since by use of the product rule of calculus
d
2
w
dr
2
+
1
r
dw
dr
=
1
r
d
dr
r
dw
dr
this can be integrated twice to obtain
w =
1
4
p
z
−g cos
r
2
+c
1
ln r +c
2
(5.1.11)
a
b
Figure 5.1.3 Rotating Couette flow—inner and outer cylinders

5.1 Solutions to the Steady-State Navier-Stokes Equations When Convective Acceleration Is Absent 145
If w = W
a
at r = a and w = W
b
at r = b, proceeding as in the plane Poiseuille flow
case, we have
w =
1
4
p
z
−g cos
r
2
−b
2
−b
2
−a
2
ln r/b
ln a/b
+W
b
+W
b
−W
a
ln r/b
ln a/b
(5.1.12)
with a shear stress
rz
=
dw
dr
=
1
4
p
z
−g cos
2r −
b
2
−a
2
r ln a/b
+
W
b
−W
a
r ln a/b
(5.1.13)
If there is no inner cylinder a =0, all logarithmic terms in equation (5.1.12) must
be ruled out, since they would make both the velocity and the shear stress infinite at
r = 0. In that case the solution reduces to
w =
1
4
p
z
r
2
−b
2
+W
b
(5.1.14)
with
zr
=
dw
dr
=
r
2
p
z
−g cos
(5.1.15)
If, instead, the outer cylinder is removed, no solution exists that is bounded at large
r. Thus, if a long cylinder is moved longitudinally through a fluid, one-dimensional
motion, depending only on r is impossible.
5.1.4 Poiseuille Flow in Conduits of Arbitrarily Shaped Cross-Section
Except for conduits of a few simple geometries, such as the circle, ellipse, rectangle, and
equilateral triangle, exact solutions of equation (5.1.6) are impossible to find. However,
the discharge can still be estimated very accurately. From the definition of Q we have
Q =
S
udS (5.1.16)
Rewrite equation (5.1.6) as
p
x
−g cos =
2
u
y
2
+
2
u
z
2
For convenience, let K =−/
p
x
−g cos , where K is a positive constant. Dividing
this equation by the negative of the pressure gradient and gravity term, we have
1 =−K
2
u
y
2
+
2
u
z
2
=−K
2
u (5.1.17)
Multiply equation (5.1.17) by u, and integrate over the conduit area, giving
Q =
S
udS =−K
S
u
2
udS =−K
S
·uu −u
2
dS = K
S
u
2
dS
(5.1.18)
where we have used the product rule of calculus, then the divergence theorem, and
finally the no-slip boundary condition.
146 Exact Solutions of the Navier-Stokes Equations
To get the first estimate on Q, choose an approximation to the velocity that
satisfies the continuity equation and the no-slip boundary conditions but not nec-
essarily the momentum equation (5.1.17). Then, by some elementary algebra and
rearrangements,
1
2
K
S
v
2
−u
2
dS =
1
2
K
S
v −u
2
+2v ·u −2u
2
dS
=
1
2
K
S
v −u
2
+2u ·v −udS
=
1
2
K
S
v −u
2
+2v −u ·u −2v −u
2
udS
=
1
2
K
S
v −u
2
dS +
S
v −udS ≥
S
v −udS
Rewriting this and using equation (5.1.17), we have
1
2
K
S
v
2
−u
2
dS −
1
2
Q ≥
S
vdS −Q
or after rearrangement,
Q ≥2
S
vdS −K
S
v
2
dS (5.1.19)
the equal sign holding only if v = u everywhere.
A different bound on Q can be found by choosing an approximation w for the veloc-
ity that satisfies equation (5.1.6) but not necessarily the no-slip boundary conditions.
Proceeding as before,
1
2
K
S
w
2
−u
2
dS =
1
2
K
S
w −u
2
+2u ·w −udS
=
1
2
K
S
w −u
2
+2u ·w −u −2u
2
w −udS
=
1
2
K
S
w −u
2
dS ≥ 0
by virtue of both u and w satisfying equation (5.1.6) and u also satisfying the no-slip
conditions. Expanding the term on the left of the inequality, and using equations (5.1.16)
and (5.1.18), the result is
1
2
K
S
w
2
dS −
1
2
Q ≥0
or finally,
Q ≤K
S
w
2
dS (5.1.20)
Again, the equal sign holds only if w equals u everywhere. Thus, from equations (5.1.19)
and (5.1.20) Q is bounded on both sides according to
K
S
w
2
dS ≤ Q ≤
S
2v −Kv
2
dS (5.1.21)
By refining the approximating functions v and w, we can come as close to u, or at least
to Q, as we desire.

5.2 Unsteady Flows When Convective Acceleration Is Absent 147
5.1.5 Couette Flow Between Concentric Circular Cylinders
For flow between concentric circular cylinders, again use cylindrical polar coordinates
and let v =0 vr 0. This satisfies continuity automatically. Then the Navier-Stokes
equations reduce to
0 =
2
v
r
2
+
1
r
v
r
−
v
r
2
v
2
r
=
p
r
(5.1.22)
The first equation is of Euler type, and its solutions are therefore of the form r
n
.
Substituting this form into equation (5.1.22a), we find that n −1n +1 =0. Thus, the
solution is
v = Ar +B/r (5.1.23)
The term multiplied by the constant A represents a rotational rigid body rotation. The
term multiplied by B is an irrotational vortex, which we saw in Chapter 2. If v =b
b
at r = b and v =a
a
at r = a, applying these boundary conditions to equation (5.1.23)
gives for A and B
A =
b
2
b
−a
2
a
b
2
−a
2
B =
a
2
b
2
a
−
b
b
2
−a
2
(5.1.24)
Notice that if a
2
a
=b
2
b
, the flow is irrotational, so viscous flows can in rare cases
be irrotational. Generally, however, they are rotational because, except for very special
boundary conditions such as we have here, vorticity is generated at boundaries by the
no-slip condition and then is diffused throughout the flow by viscosity.
If the outer cylinder is absent, A = 0, which again is an irrotational flow. If the
inner cylinder is absent, B = 0, and the motion is a rigid body rotation.
5.2 Unsteady Flows When Convective Acceleration Is Absent
Next consider two important cases of unsteady flow that were first solved by Stokes.
Both of the problems have a velocity of the form v =uy t 0 0 and an infinite plate
located at y =0. For these flows, since the flow is due solely to the motion of the plate
and no other forcing is imposed, the pressure gradient is absent, and the x momentum
equation becomes
u
t
=
2
u
y
2
(5.2.1)
5.2.1 Impulsive Motion of a Plate—Stokes’s First Problem
Stokes considered the case where at an initial time a plate is suddenly caused to move
in the x direction with a velocity U . Considering the various parameters in the problem,
we see that u must depend only on y, t, U, , and . Thus, we have u =uy t U .
In dimensionless form this can be written as
u
U
=f
y
t
Uy
(5.2.2)
148 Exact Solutions of the Navier-Stokes Equations
Since the momentum equation (5.2.1) in this case is linear, and since U appears only in
the boundary condition, expect that U will appear only as a multiplying factor, so the
dimensionless form (5.2.2) can be reduced to
u
U
=f
y
t
(5.2.3)
To verify this, note that
u
t
=−
Uy
2t
t
f
u
y
=U
t
f
, and
2
u
y
2
=
U
t
f
, where a prime
denotes differentiation with respect to the dimensionless variable =y
√
/t. Inserting
the preceding into equation (5.2.1), the result is −
Uy
2t
t
f
=
U
t
f
,or
f
+05 f
=0 (5.2.4)
The boundary conditions on f are as follows: Because of the no-slip condition,
u = U on the flat plate, which requires that f0 = 1. At very large values of y u
must go to zero, since the velocity is transported away from the plate only by viscous
diffusion, and it will take a very large amount of time for the effect to be noticed away
from the plate. Therefore, f =0.
Equation (5.2.4) can be integrated once to give f
= A exp−
2
/4, where A is a
constant of integration. Integrating this once again gives f = A
0
e
−
2
/4
d +B, where
B is a second constant of integration. Since f0 =1B=1. Since f =0,
0 = A
0
e
−
2
/4
d +1giving A =
−1
0
e
−
2
/4
d
The integral appearing in the denominator of A has the value
√
; thus, A =−1/
√
and finally
u =U
1−Err
=U ∗Errc (5.2.5)
where Err =1/
√
0
e
−
2
/4
d. The integral appearing in equation (5.2.5) is a form
of the well-known error function, and 1 minus the error function is the complementary
error function. Typical values for the solution are seen in Table 5.2.1 and in Figure 5.2.1.
The combination 1 −u/U corresponds to the case where the plate is at rest and the
outer fluid is impulsively started in motion.
TABLE 5.2.1 The Error Function
u/U 1−u/U u/U 1 −u/U u/U 1 −u/U
0010000 00000 1303580 06420 2600660 09340
0109436 00564 1403222 06778 2800477 09523
0208875 01125 1502888 07112 3000339 09661
030832 01680 1602579 07421 3200236 09764
0407773 02227 1702293 07707 3400162 09838
0507237 02763 1802031 07969 3600109 09891
0606714 03286 1901791 08209 3800072 09928
0706206 03794 2001573 08427 4000047 09953
0805716 04284 2101376 08624 4200030 09970
0905245 04755 2201198 08802 4400018 09982
1004795 05205 2301039 08961 4600011 09989
1104367 05633 24009 09103 4800007 09993
1203961 06039 250077 09229 5000004 09996

5.2 Unsteady Flows When Convective Acceleration Is Absent 149
0.8
1.0
0.6
0.4
0.2
0.0
012
Zeta
Complementary
Error Function
Error Function
345
Figure 5.2.1 Error and complementary error functions
The variable that appears in this solution is called a similarity variable, and f is
called a similarity solution.Bysimilarity we mean that at two different times, t
1
and t
2
,
we have geometric similarity in our flow (one velocity profile is merely an enlargement
of the other) at locations y
1
and y
2
, providing that
y
1
t
1
=y
2
t
2
or equivalently,
1
=
2
. (5.2.6)
Similarity solutions play an important role in fluid mechanics. It reduces the Navier-
Stokes partial differential equations to ordinary differential equations that are much
easier to solve, with a solution that is much easier to understand physically. The existence
of a similarity solution depends on simplifying conditions such as the domain having
infinite extent, which allows the number of dimensionless parameters to be small. Thus,
the similarity solutions are very special solutions and exist only in a relatively few flow
cases. We will see more of similarity solutions in later sections.
This Stokes problem is a reasonably good approximation of the flow on a flat plate if
we consider Ut to be a “distance” from the leading edge of the plate. To see how “deep”
the viscous effects penetrate, note that for = 3 the fluid velocity is reduced to less
than 4% of the plate velocity. Consequently, we can consider this to be approximately
the outer edge of the effects of viscosity. This thickness is termed the boundary layer
thickness. In terms of distance from the leading edge of the plate, we have
boundary layer thickness =3
t/ =3
x/U =3x/
Ux/, (5.2.7)
We will consider the problem of flow on a flat plate again in Chapter 6 and find it to
be in general agreement with those results.
5.2.2 Oscillation of a Plate—Stokes’s Second Problem
A second problem considered by Stokes is one where an infinite plate oscillates back
and forth with a circular frequency , the motion having taken place sufficiently long
that the starting conditions can be ignored. Then, u0t=U cos t, with U being the
maximum speed of the plate.

150 Exact Solutions of the Navier-Stokes Equations
If we were to try to solve this problem using separation of variables, the “traditional”
method of solving partial differential equations, we would find phase differences in time
between the boundary velocity and the fluid velocities, and we would need both the
sine and cosine of t. The result would be that we would end up having to solve two
coupled second order equations. An easier approach is to let u0t=Ue
it
, where i is
the imaginary number
√
−1, and by DeMoivre’s theorem e
it
= cost +i sint.
Since the real part of e
it
is cos t, our solution is found by taking only the real part
of u at the very end of our analysis.
Proceeding in this manner, let
u =fye
it
(5.2.8)
and substitute this into equation (5.7.8). The result is
if =f
(5.2.9)
with the solution
f =Ae
−1+iy/a
+Be
1+iy/a
(5.2.10)
where a =
12/ is a characteristic length for the problem. The parameter a tells
us how far the viscous effects penetrate from the boundary into the fluid.
Because of the condition at y =0, we have A+B =U . If we consider the only solid
boundary to be at y =0, then u must vanish as y becomes large. Since the term that B
multiplies grows exponentially as y increases, then the requirement is met if B =0isto
be everywhere finite. Then it follows that A = U and uy t = Ue
−1+iy/a +it
. Taking
the real part of this gives
uy t = Ue
−y/a
cost −y/a (5.2.11)
If there were a solid boundary at y =b instead, then ub t =0 and 0 =Ae
−1+ib/a
+
Be
1+ib/a
. Solving for A and B yields
fy =U
e
1+ib−y/a
−e
−1+ib−y/a
e
1+ib/a
−e
−1+ib/a
=U
sinh
1+ ib −y
a
sinh
1+ ib
a
(5.2.12)
Notice that if a is small, the limit of equation (5.2.12) is f ≈ Ue
−1+iy/a
, which says
that the fluid motion is confined to a thin region near the wall with thickness of order a.
In fact, equation (5.2.12) shows us that when b ≥ 2a, and since e
−2
≈01, for practical
purposes the upper plate can be thought of as being at infinity for such values of a.
The results of Stokes’s second problem are important to the study of pulsatile flows.
There are few analytical tools available to deal with these flows, and Stokes’s solution
at least indicates some of the primary effects that can occur.
Example 5.2.1 Work done in an oscillating flow
An acoustic pressure p
0
sin x/c sin t is set up in a gas that has a speed of sound
c. This in turn induces a velocity field U
0
cos x/c cos t, where U
0
=p
0
/c.No
useful work is produced by this, since the pressure and velocity are 90 degrees out of
phase. Show that by introducing a flat plate into the flow and parallel to the velocity
field, useful work is produced.

5.2 Unsteady Flows When Convective Acceleration Is Absent 151
Solution. Assume the following: The plate is long enough that edge effects can be
ignored; the viscous terms in the Navier-Stokes equations that involve second derivatives
with respect to x can be neglected compared to the terms involving second deriva-
tives with respect to y. The justification of this is that a boundary layer exists. The
equation that will govern the flow and use the preceding assumption on the viscous
terms is
u
t
=−
p
x
+
2
u
x
2
This is the counterpart of equation (5.2.1) that, however, also includes the pressure
gradient term. As suggested by Stokes’s second solution and the far field, take
ux y t =U
0
1+fy cosx/ce
it
px t =−ip
0
sinx/ce
it
the −i in front of the pressure taking care of the time phase difference. Again, real
values will be taken after solving for f.
Substituting these forms into the governing equation, we have, after cancelling
out the common x and t factors, that iU
0
1 +f=−p
0
/c +U
0
f
. By virtue
of the relation between U
0
and p
0
, the constant terms cancel. Thus, we are left with
if = f
the same as equation (5.2.9). Again, take the solution that decays as y
increases. Thus, f =Ae
−1+iy/a
, where a is defined as in Stokes’s second problem.
Applying the boundary condition gives A =−1. Thus,
ux y t =U
0
1−e
−1+iy/a
cosx/ce
it
which satisfies all boundary conditions. Taking the real part, we have for the final form
of the velocity
ux y t =U
0
1−e
−y/a
cosy/acost −e
−y/a
siny/asintcosx/c
The useful local work LW performed over a period T =2/ is
LW =
1
T
T
0
pu dt.
Putting our expressions for pressure and velocity, we have
LW =
1
T
T
0
p
0
sinx/c sintU
0
1−e
−y/a
cosy/a cost
−e
−y/a
siny/a sint cosx/cdt
The time terms that involve the product of the sine and cosine will average to zero over
the interval, while the average of the sine squared terms is T/2. Thus, we have
LW =−05e
−y/a
siny/a cosx/c.
Notice that the term independent of y, which represents the work done in the far field,
dropped out of LW. The total work TW per unit width and length is
TW =
0
LW dy =−05p
0
U
0
cosx/c
0
e
−y/a
siny/a dy =−025p
0
U
0
cosx/c
Thus useful work is done due to the phase shift introduced in the velocity field by
the no-slip condition and the presence of the plate. The results given here are a much
simplified version of a device known as the “acoustic refrigerator.”

152 Exact Solutions of the Navier-Stokes Equations
5.3 Other Unsteady Flows When Convective Acceleration
Is Absent
5.3.1 Impulsive Plane Poiseuille and Couette Flows
Several of the flows in the first section of this chapter can also be solved for if they
are unsteady flows. For the plane Poiseuille flow, suppose that the fluid is initially at
rest, and then suddenly the pressure gradients and plate motions are applied with the
walls held still. Then v = uy t 0 0, and a u/t term must be included in the
acceleration. It is convenient now to let u = u
s
+u
t
, where u
s
is given by equation
(5.1.2) and u
t
is the transient solution. Then, by the linearity of the equations, and
getting =/,
u
t
t
=
2
u
t
y
2
(5.3.1)
and u
t
=−u
s
at t =0, with u
t
=0aty = 0 and y =b.
Separation of variables along with application of the boundary conditions yields
u
t
=
n=1
A
n
e
−n
2
2
t/b
2
sin
ny
b
(5.3.2)
Applying the initial condition and using the orthogonality of the sine function gives
A
n
=
−
b
0
u
s
sin
ny
b
dy
b
0
sin
2
ny
b
dy
(5.3.3)
For stationary walls u
x
=
1
2
p
x
−g cos
y
2
−by
, giving
A
n
=−
2
b
p
x
−g cos
b
n
3
1−−1
n
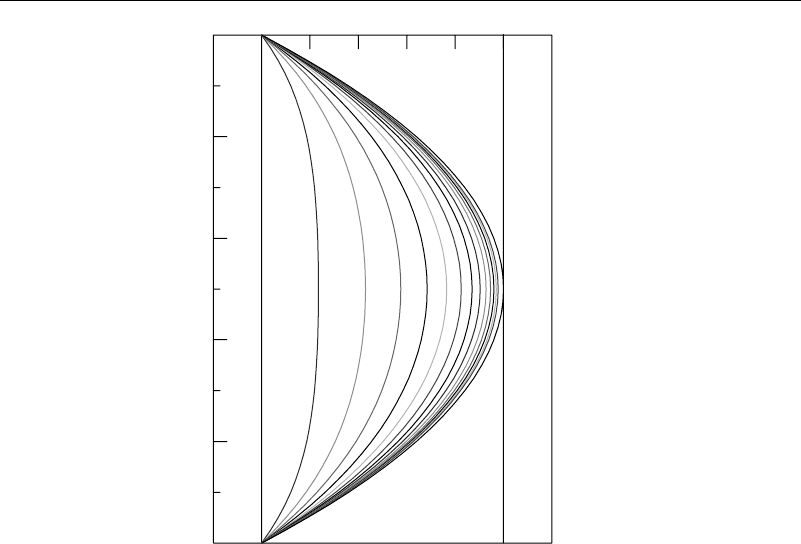
A plot of the developing flow showing velocity profiles as time passes is shown in
Figure 5.3.1.
The solution given by equation (5.3.2) is for a step function increase in the driving
force p/x −g sin . From this solution the velocity for a driving force that is an
arbitrary function of time can easily be found. Let u
u
= u
su
y +u
tu
y t, where the
subscript u stands for our solution (5.3.2) with p/x −g sin set to unity. For an
arbitrary forcing function p/x −g sin =ft, Duhamel’s superposition theorem
1
can be used to give the velocity
uy t = u
u
t
0
+
t
t
0
u
u
y
ft −d (5.3.4)
Thus, only a single time integration is needed to find the velocity for the arbitrary
forcing function.
1
Duhamel’s theorem is similar to the convolution theorem encountered in the use of Fourier integrals.
5.3 Other Unsteady Flows When Convective Acceleration Is Absent 153
0.8
1.0
0.6
y
/b
0.4
0.2
u
(
y, t
)/Umax
0.0
Figure 5.3.1 Developing plane Couette flow—two dimensions
5.3.2 Impulsive Circular Couette Flow
For impulsively started transient Couette flow in a circular annulus a ≤ r ≤ b, take
v =0v
s
r +v
t
r t 0 with v
s
given by equation (5.2.1). Using the unsteady Navier-
Stokes equations in cylindrical polar coordinates together with separation of variables,
a procedure similar to the preceding yields
v
t
=
k
e
−k
2
t
A
k
J
1
kr +B
k
Y
1
kr
where J
1
and Y
1
are Bessel functions of the first and second kind. Application of the
boundary conditions yields
A
k
J
1
ka +B
k
Y
1
ka =0
A
k
J
1
kb +B
k
Y
1
kb =0
Solving these for A and B, find that
B
k
=−A
k
J
1
ka/Y
1
ka (5.3.5)
and
J
1
kbY
1
ka −J
1
kaY
1
kb =0 (5.3.6)
Equation (5.3.6) determines the characteristic values of k that are to be used in the
summation.
